Тигонометрические функции и их графики

1. Тригонометрические функции

и их графики

2.

Построение графика функции y = sinx с
применением тригонометрического круга
p - шесть клеток
О
2p
с
5p 3
ь
6
p
II
p
2
I
и
н
III
у
3
1
С
y
p
p
6
0
IY
-p
-5p
с -1
6
6 -2p
p
о-p
3
3 2
в
1
0
-p
2
-p
-5p -2p
3
6
III
p
-p
3
-p
6
IY
0
-1
p x
2
p
p
6
3
I
2p
3
5p
6
II

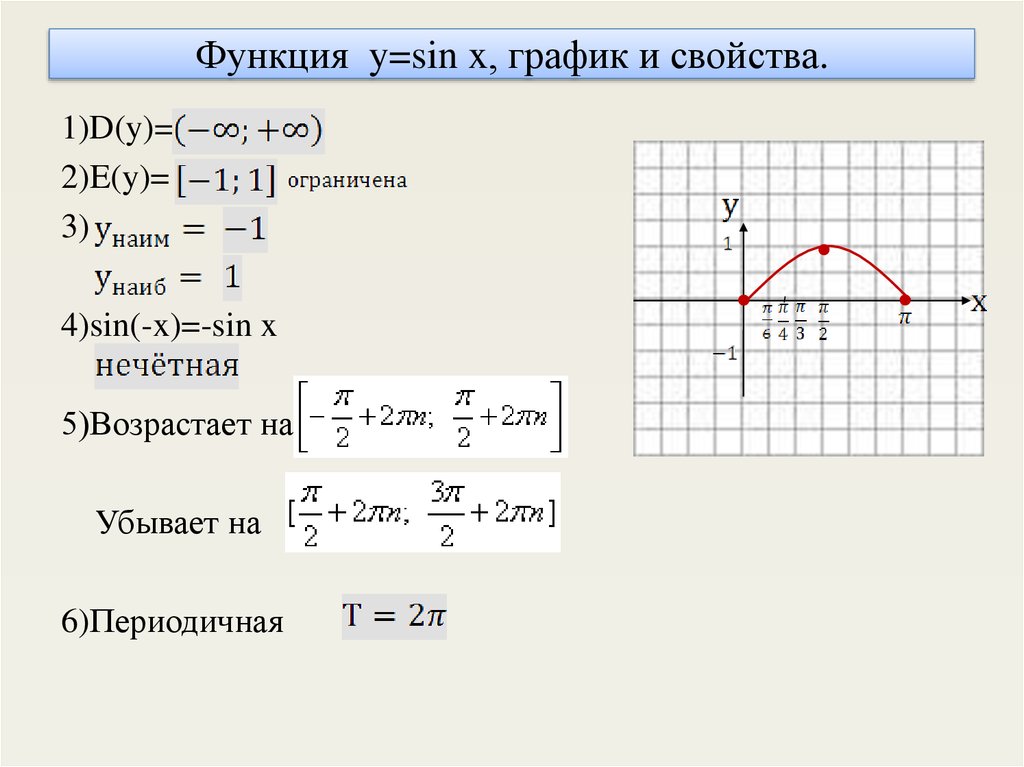
3. Функция y=sin x, график и свойства.

1)D(y)=
2)E(y)=
3)
4)sin(-x)=-sin x
5)Возрастает на
Убывает на
6)Периодичная

4. Знаки синуса

1. Синус равен нулю при
,
где n - любое целое число;
2. Синус положителен при
где n - любое целое число;
3. Синус отрицателен
при
, где n - любое
целое число.
,

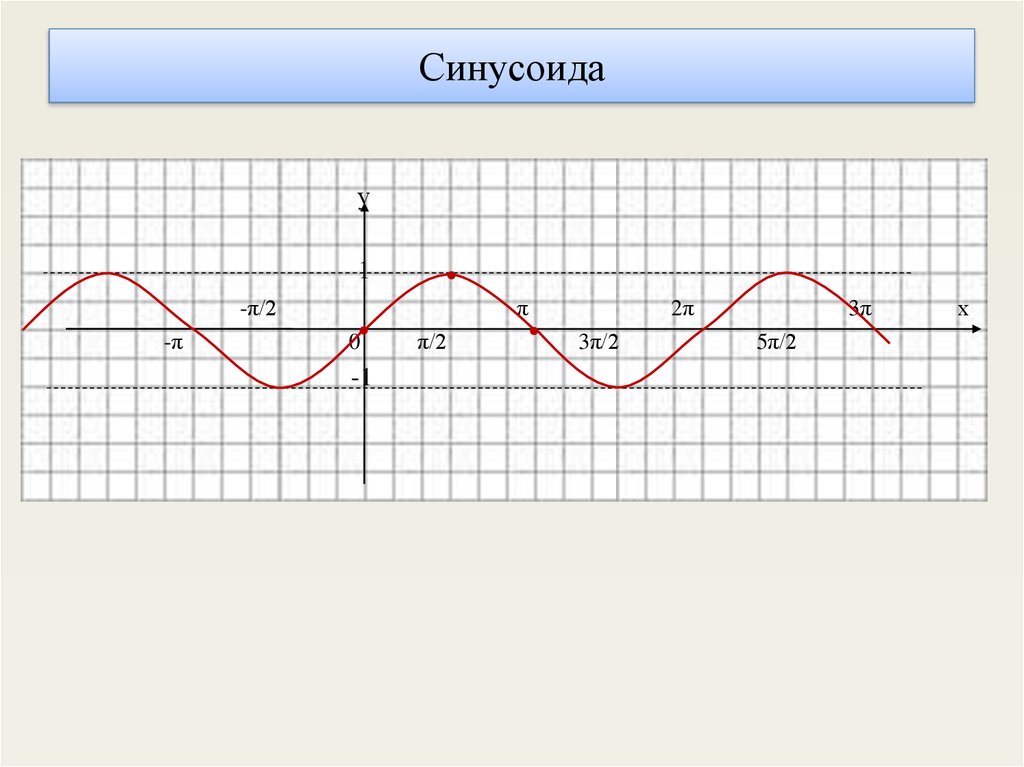
5. Синусоида

у
1
π
-π/2
-π
0
-1
π/2
2π
3π/2
3π
5π/2
х

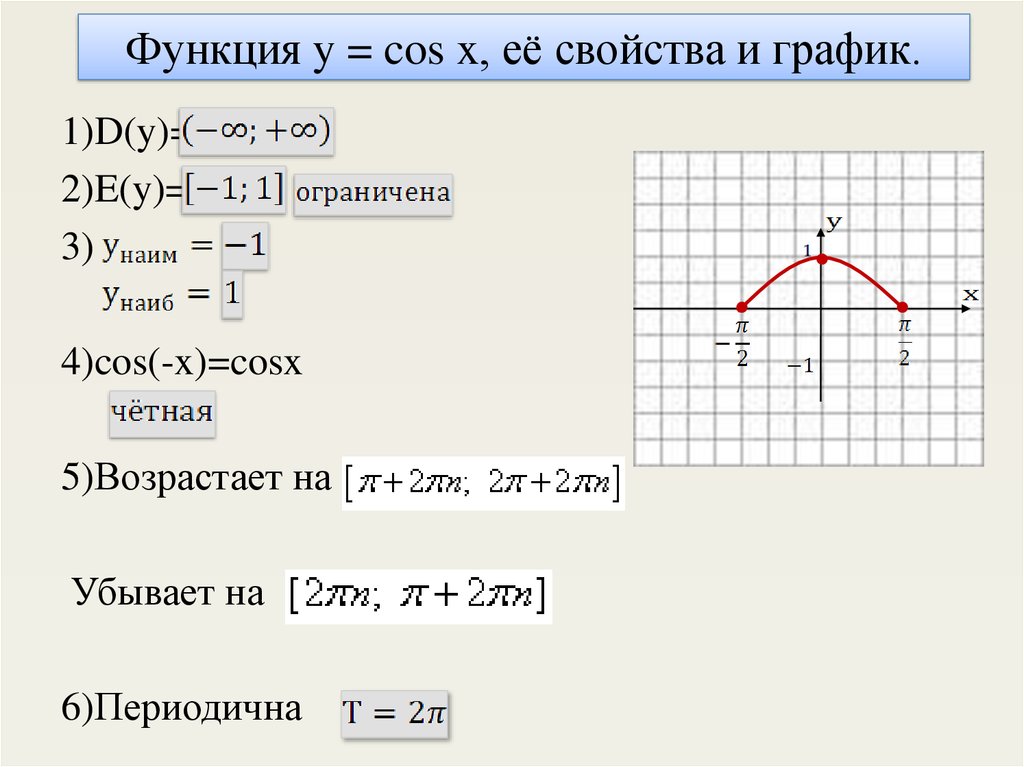
6. Функция y = cos x, её свойства и график.

1)D(y)=
2)E(y)=
3)
4)cos(-x)=cosx
5)Возрастает на
Убывает на
6)Периодична

7. Знаки косинуса

1.косинус равен нулю при
2.косинус положителен при
3. косинус отрицателен при
где n - любое целое число.

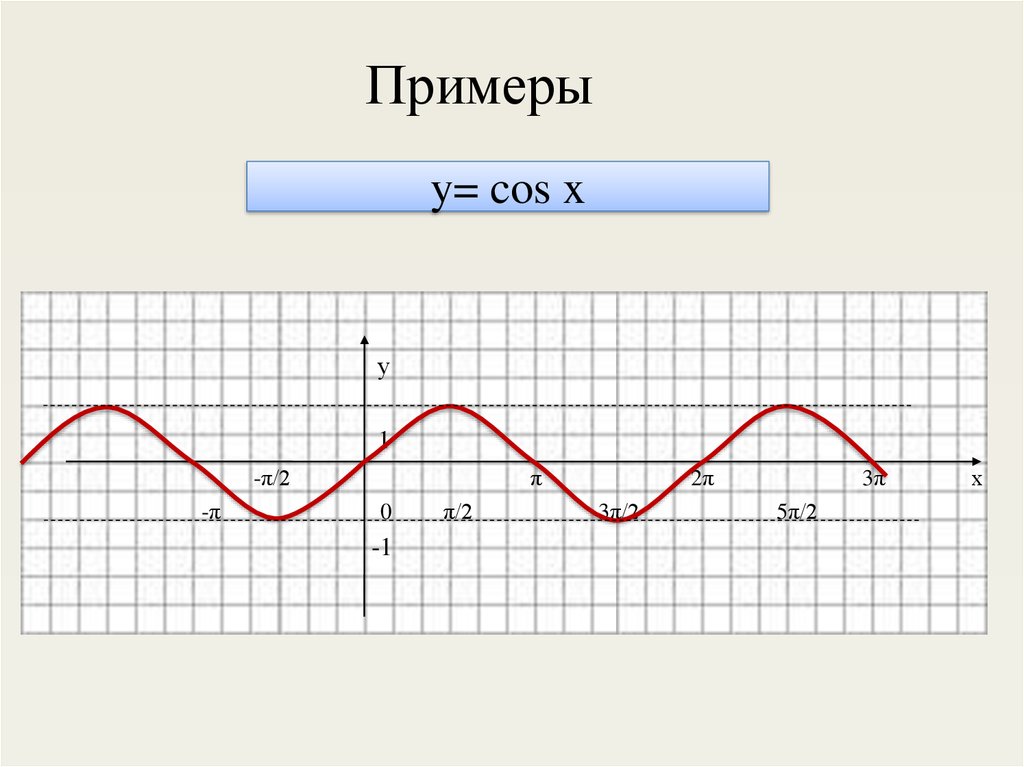
8. y= cos x

Примеры
y= cos x
у
1
π
-π/2
-π
0
-1
π/2
2π
3π/2
3π
5π/2
х

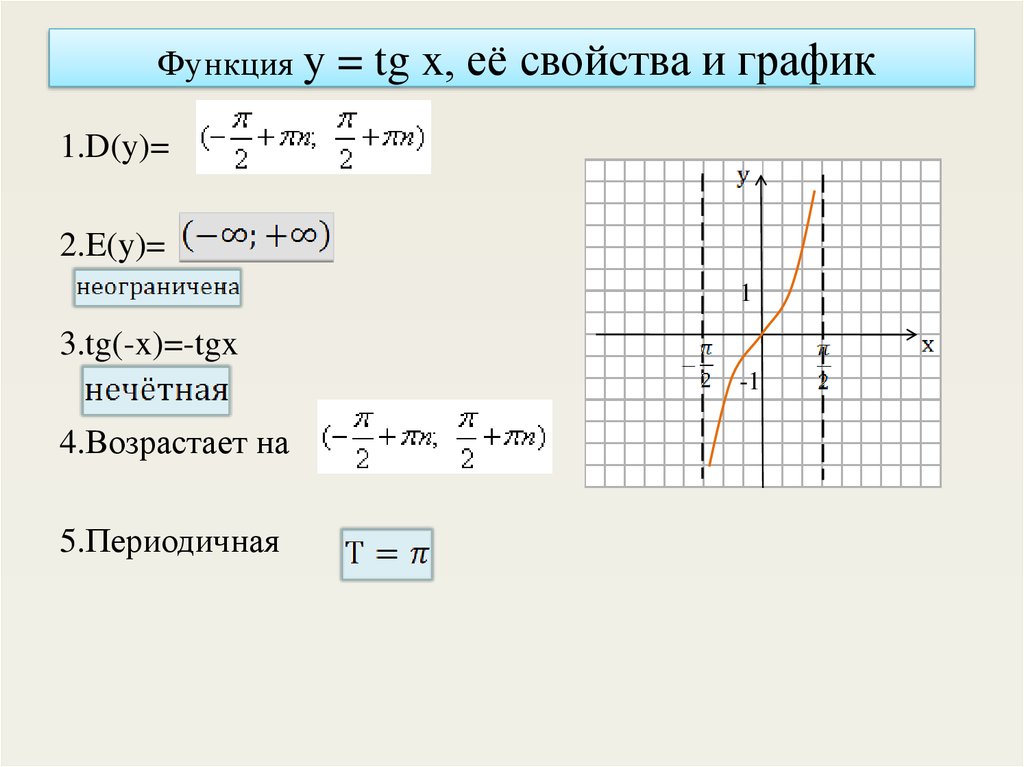
9. Функция y = tg x, её свойства и график

1.D(y)=
2.E(y)=
1
3.tg(-x)=-tgx
-1
4.Возрастает на
5.Периодичная

10. Знаки тангенса

1.равен нулю, когда синус равен нулю,
то есть при
, где n - любое целое число.
2.положителен, когда синус и косинус
имеют одинаковые знаки.
Это бывает только в первой и в
третьей четвертях, то есть при
где а- любое целое число.
3.отрицателен, когда синус и косинус имеют
разные знаки.
Это бывает только во второй и в
четвертой четвертях, то есть при
где а - любое целое число.

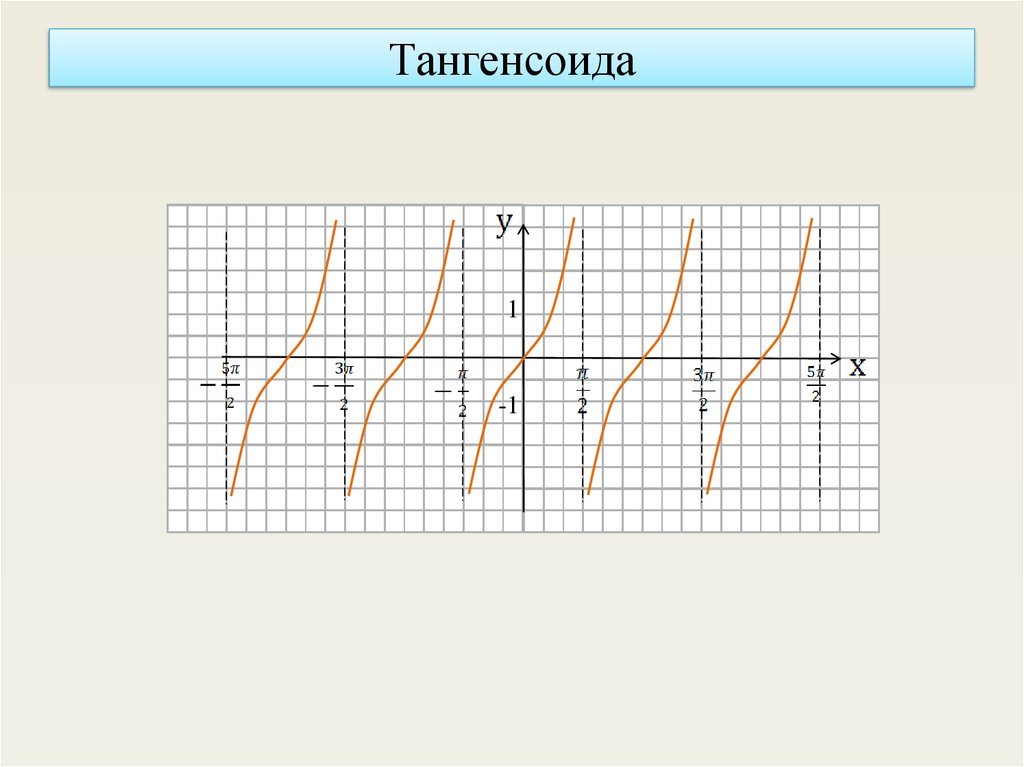
11. Тангенсоида

1
-1

12. Функция y = сtg x, её свойства и график

Функция y
1.D(y)=
2.E(y)=
3.ctg(-x)=-ctgx
4.Убывает на
5.Периодичная
= сtg x, её свойства и график

13. Знаки котангенса

1.равен нулю, когда косинус равен нулю,
то есть при
2.положителен, когда синус и косинус имеют
одинаковые знаки. Это бывает только в первой и
в третьей четвертях, то есть при
3.отрицателен, когда синус и косинус имеют
разные знаки. Это бывает только во второй и в
четвертой четвертях, то есть при

14. Домашнее задание

Колмогоров А.Н. Алгебра и начала анализа,
стр.14 §1 п.2, стр. 20 № 33(а,б).