Similar presentations:
Тригонометрические функции
1. Тригонометрические функции
Урок № 11Тригонометрические функции
ОДА ФУНКЦИИ
На первый взгляд, понятие не ново,
И не всегда подумаешь о том,
Как важно будет в жизни это слово
И сколько смысла будет в слове том!
Его по-разному с годами толковали.
Сам Лобачевский руку приложил,
Чтоб слово «функция» и в средней школе знали,
Чтоб каждый ученик им дорожил!
Без функции не сдашь простой экзамен,
Без функции ты не войдешь в предмет!
Без функции не разгорится пламя!
Без функций никакой науки нет!
И.Кушнир, Л.Финкельштейн
2.
Функция – зависимостьy
от x
x
y
аргумент
функция
независимая переменная
зависимая переменная
область определения
функции
D(y)
множество значений
функции
E(y)
Способы задания функции
y=f(x)
аналитический
табличный
графический
3.
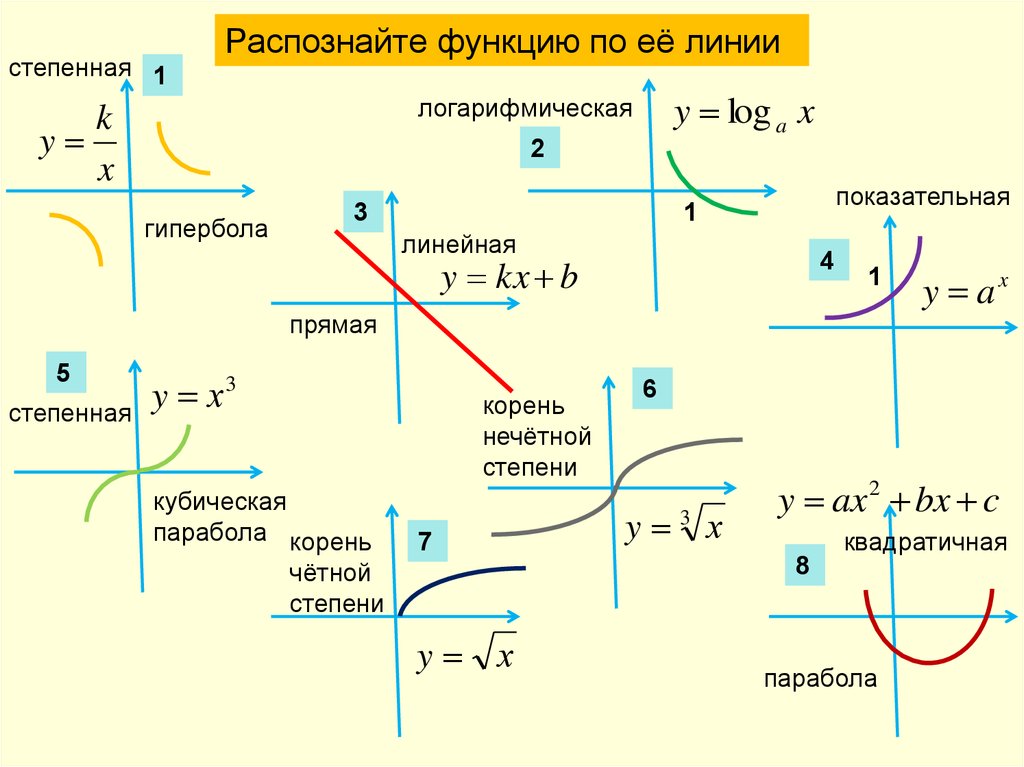
степенная 1Распознайте функцию по её линии
y log a x
логарифмическая
k
y
x
2
гипербола
3
показательная
1
линейная
4
y kx b
1
прямая
5
степенная
y х3
корень
нечётной
степени
кубическая
парабола корень
7
6
y 3 х
y ax 2 bx c
квадратичная
8
чётной
степени
y х
y ax
парабола
4.
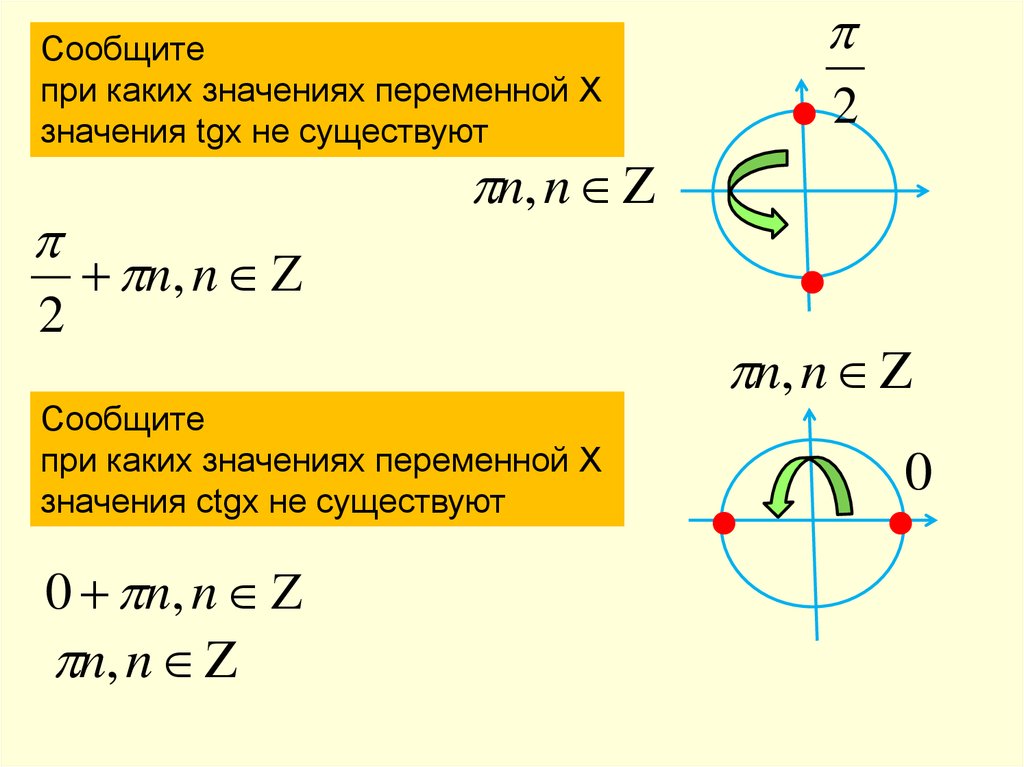
Сообщитепри каких значениях переменной Х
значения tgx не существуют
2
2
n, n
n, n
Сообщите
при каких значениях переменной Х
значения сtgx не существуют
0 n, n
n, n
n, n
0
5. Область определения и множество значений тригонометрических функции
y=sinx,y=cosx,
y=tgx,
y=ctgx
функция
D(y): х
E(y): y
y=sinx
R или (-∞;∞)
[-1;1]
y=cosx
R или (-∞;∞)
[-1;1]
y=tgx
R,кроме π/2+πn,nϵZ
R или (-∞;∞)
y=ctgx
R,кроме πn,nϵZ
R или (-∞;∞)
6.
На уроке решаем № 691(1;3;5), №693(1;3), №694(1;3;5)7.
На уроке решаем №695(1;3)8.
устноВыберите из списка функций те
которые областью определения имеют
множество всех действительных чисел
9. Домашнее задание № 11
§ 38№ 691(2;4;6), №693(2;4), №694(2;4;6), №695(2;4)







 mathematics
mathematics








