Similar presentations:
Свойства функций
1. Свойства функций
2. Схема исследования:
Область определения
Множество значений
Нули функции
Интервалы знакопостоянства
Промежутки монотонности
Точки экстремума
Набольшее и наименьшее значения
функции
3.
Область определения функцииэто важно
D( y) 8; 9
4.
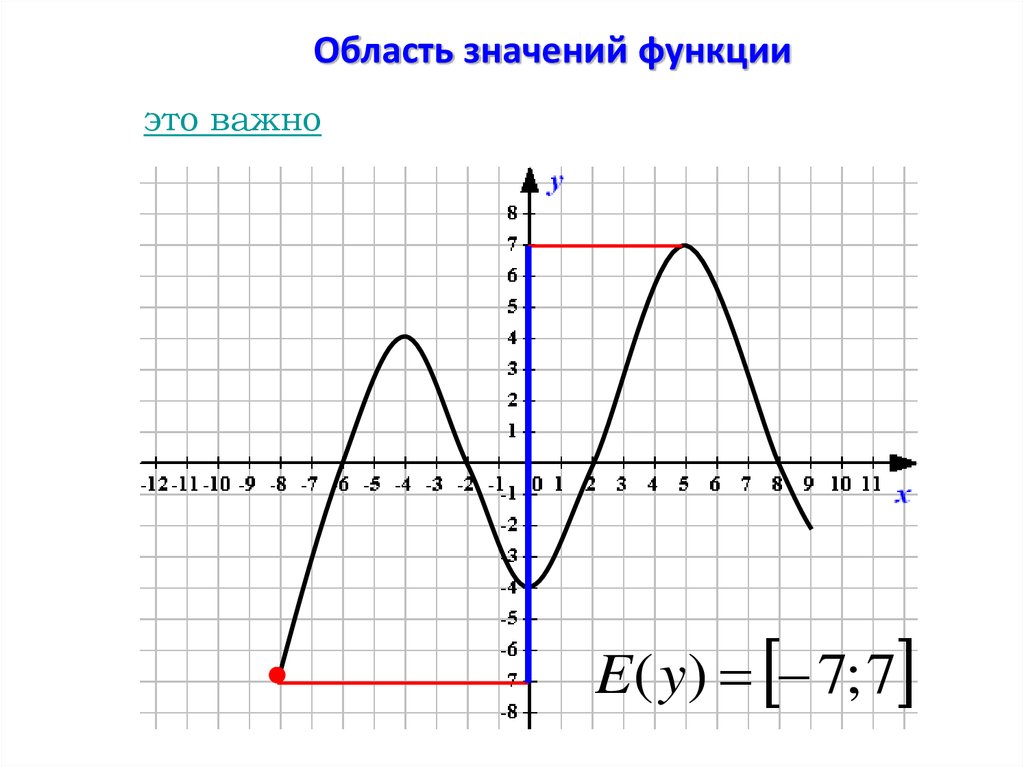
Область значений функцииэто важно
E( y) 7; 7
5.
Нули функцииэто важно
x 6; x 2;
x 2; x 8
6.
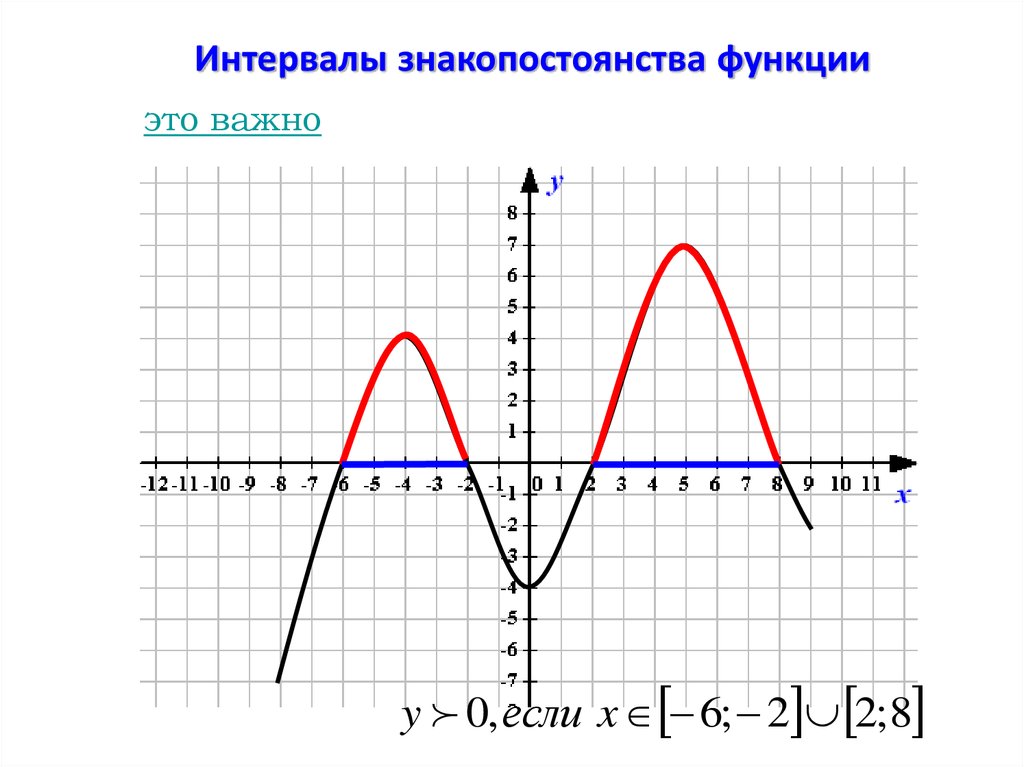
Интервалы знакопостоянства функцииэто важно
y 0, если x 6; 2 2; 8
7.
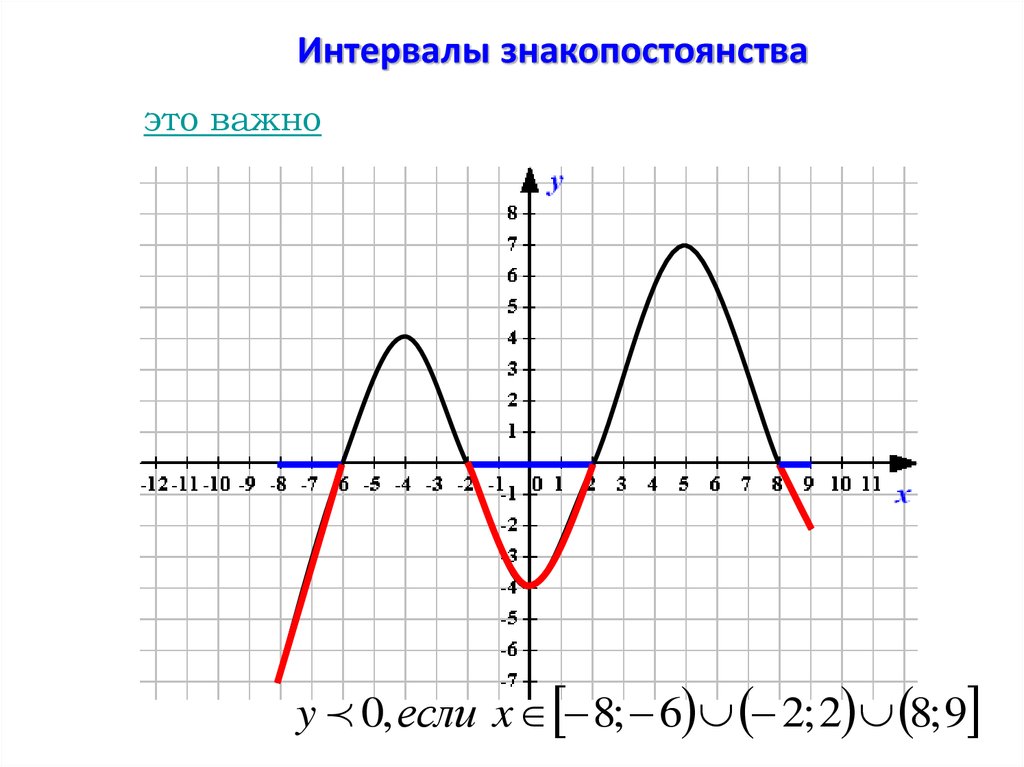
Интервалы знакопостоянстваэто важно
y 0, если x 8; 6 2; 2 8; 9
8.
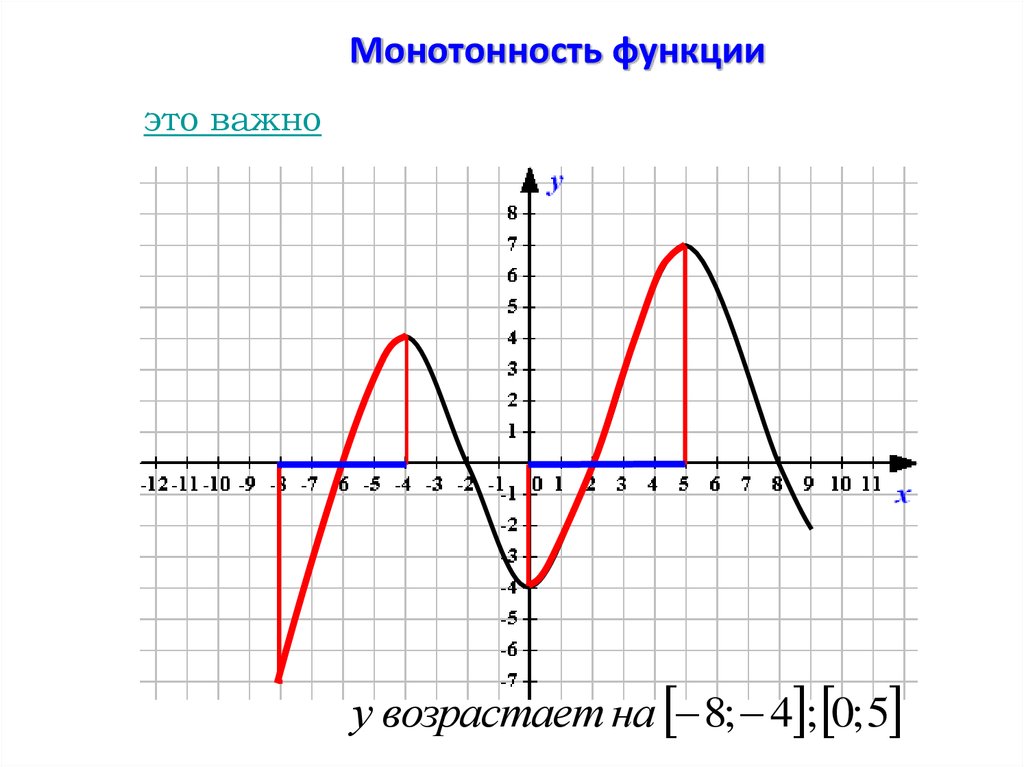
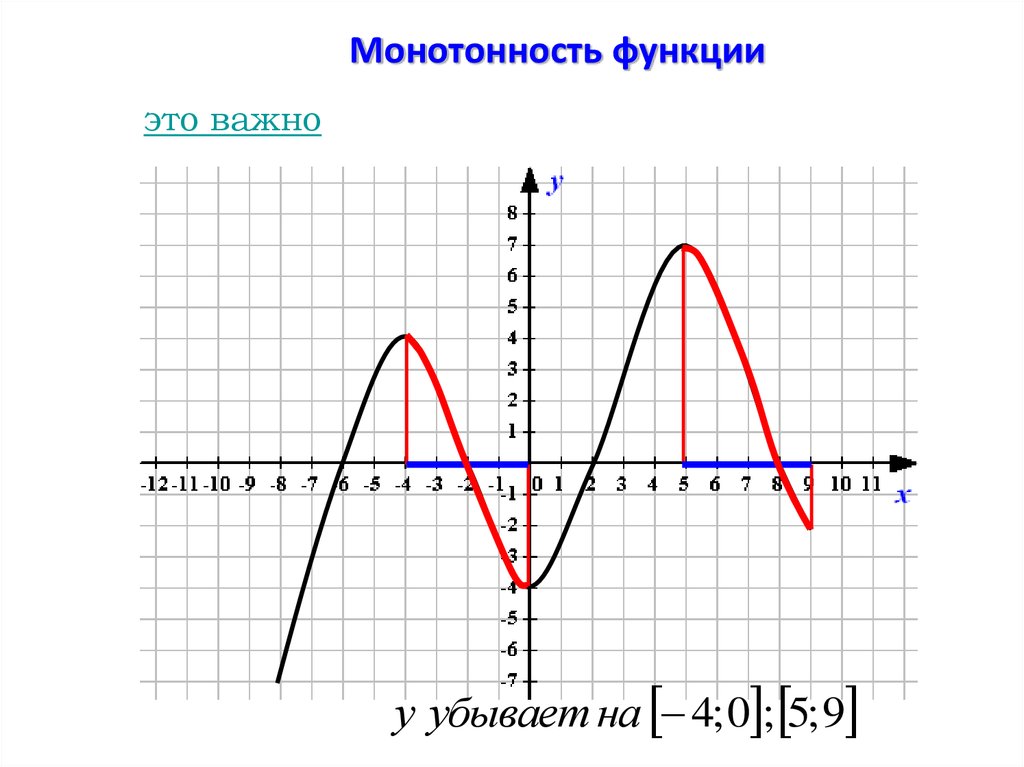
Монотонность функцииэто важно
у возрастает на 8; 4 ; 0; 5
9.
Монотонность функцииэто важно
у убывает на 4; 0 ; 5; 9
10.
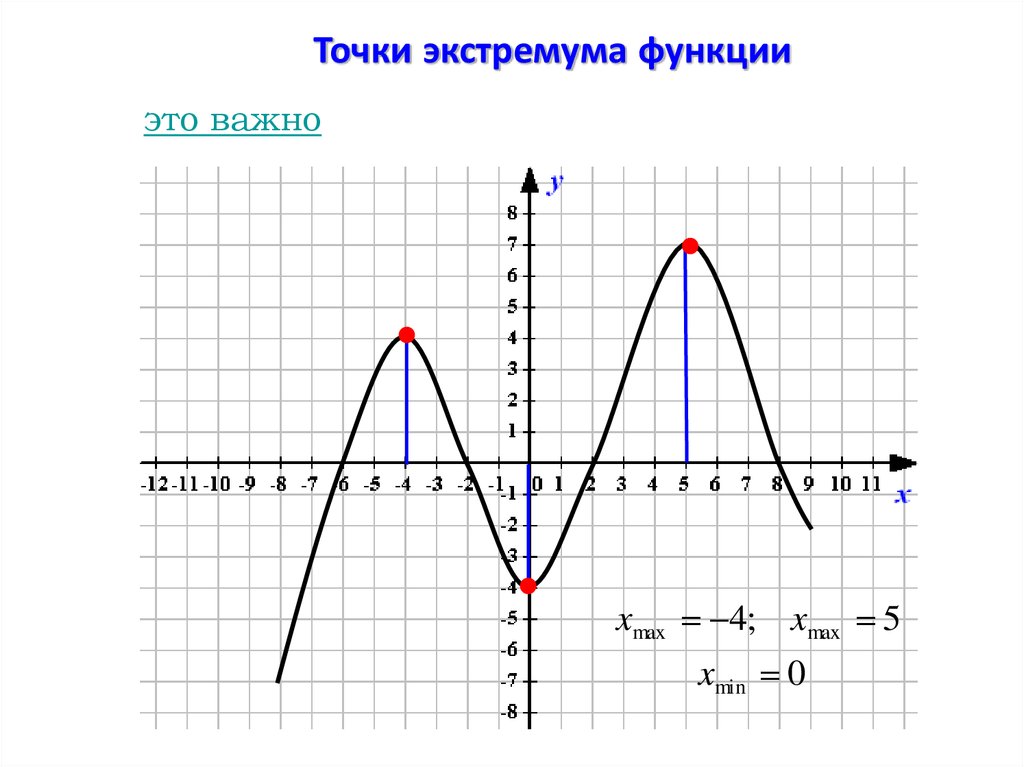
Точки экстремума функцииэто важно
xmax 4; xmax 5
xmin 0
11.
Экстремумы функцииэто важно
ymax 4;
ymax 7
ymin 4
12.
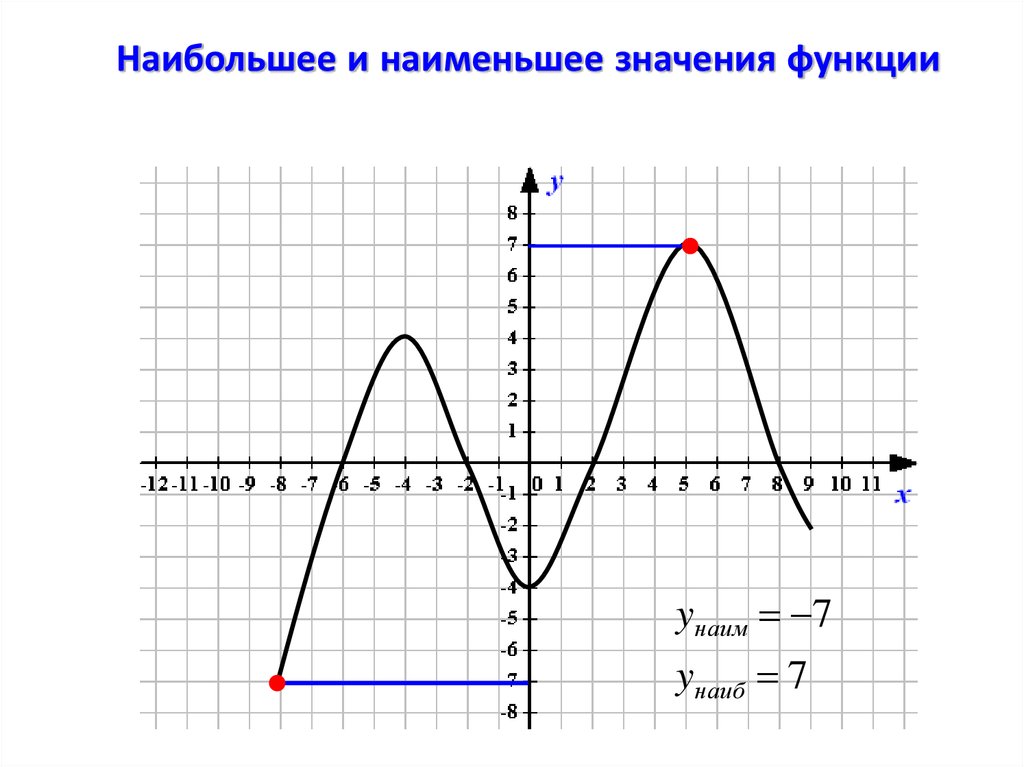
Наибольшее и наименьшее значения функцииyнаим 7
yнаиб 7
13.
14.
15.
16.
17.
Область определения функцииВсе допустимые значения
аргумента x функции y(х).
назад
18.
Область значения функцииМножество, состоящее из всех
чисел y(x), таких, что x
принадлежит области
определения функции y(х).
назад
19.
Нули функцииЭто значения аргумента х, при
которых значение функции у(х)
равно нулю.
назад
20.
Интервалы знакопостоянствафункции
Это промежутки, на которых функция
y(х) принимает положительные
(отрицательные) значения.
назад
21.
Монотонность функцииФункция y(х) убывает на множестве P,
если для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) < y (x1)
назад
Функция y(х) возрастает на множестве P,
если для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) > y (x1)
назад
22.
Точки экстремума функцииТочка x0 называется точкой минимума функции
y(х), если для всех x из некоторой окрестности
x0 выполнено неравенство
y ( x) y ( x0 )
Точка x0 называется точкой максимума функции
y(х), если для всех x из некоторой окрестности
x0 выполнено неравенство
y ( x) y ( x0 )
назад
23.
Экстремумы функцииЗначение функции в точках
максимума называют максимумом
функции.
Значение функции в точках
минимума называют минимумом
функции.
Общее название – экстремумы
функции.
назад













 mathematics
mathematics








