Similar presentations:
Свойства функции
1. Свойства функции
2.
Область определения функцииВсе допустимые значения
аргумента x функции y(х).
назад
3.
Область определения функцииD( y) 8; 9
4.
Множество значений функцииМножество, состоящее из всех
чисел y(x), таких, что x
принадлежит области
определения функции y(х).
назад
5.
Множество значений функцииE( y) 7; 7
6.
Четность или нечетностьФункцию y = f(x), х ∊ Х называют четной, если для
любого значения х из множества Х выполняется
равенство
f(-x) = f(x).
График четной функции симметричен относительно
оси ординат.
Функцию y = f(x), х ∊ Х называют нечетной, если для
любого значения х из множества Х выполняется
равенство f(–x) = – f(x).
График нечетной функции симметричен относительно
начала координат.
7.
Четность или нечетность8.
ОграниченностьФункцию у= f(x) называют ограниченной снизу на
множестве Х, если все значения этой функции на
множестве Х больше некоторого числа, т.е., если
существует такое число M, что для любого значения х
выполняется неравенство f(x) > M
Функцию у= f(x) называют ограниченной сверху на
множестве Х, если все значения этой функции на
множестве Х меньше некоторого числа , т.е. , если
существует такое число М , что для любого значения х
выполняется неравенство f(x) < М
Если функция ограничена и снизу и сверху на всей области
определения, то ее называют ограниченной.
9.
Ограниченность10.
Нули функцииЭто значения аргумента х, при
которых значение функции у(х)
равно нулю.
назад
11.
Нули функцииx 6; x 2;
x 2; x 8
12.
Интервалы знакопостоянства функцииЭто промежутки, на которых функция
y(х) принимает положительные
(отрицательные) значения.
назад
13.
Интервалы знакопостоянства функцииy 0, если x 6; 2 2; 8
14.
Интервалы знакопостоянстваy 0, если x 8; 6 2; 2 8; 9
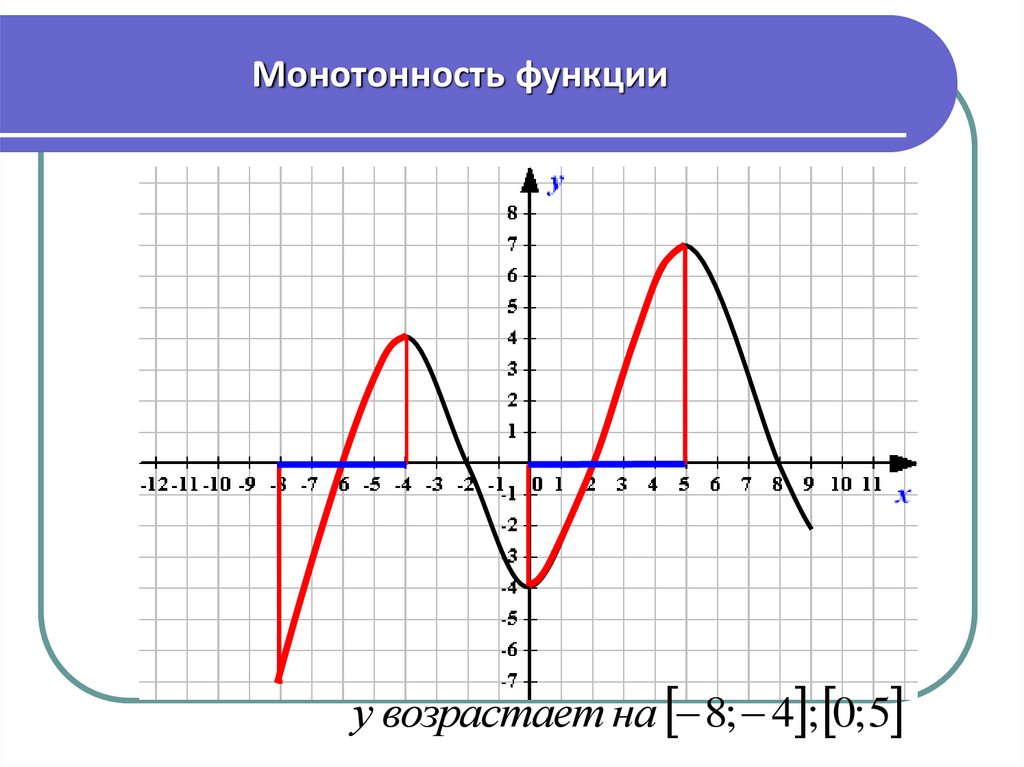
15.
Монотонность функцииФункция y(х) убывает на множестве P,
если для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) < y (x1)
назад
Функция y(х) возрастает на множестве P,
если для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) > y (x1)
назад
16.
Монотонность функцииу возрастает на 8; 4 ; 0; 5
17.
Монотонность функцииу убывает на 4; 0 ; 5; 9
18.
Точки экстремума функцииТочка x0 называется точкой минимума функции
y(х), если для всех x из некоторой окрестности
x0 выполнено неравенство
y ( x) y ( x0 )
Точка x0 называется точкой максимума функции
y(х), если для всех x из некоторой окрестности
x0 выполнено неравенство
y ( x) y ( x0 )
назад
19.
Точки экстремума функцииxmax 4; xmax 5
xmin 0
20.
Экстремумы функцииЗначение функции в точках
максимума называют максимумом
функции.
Значение функции в точках
минимума называют минимумом
функции.
Общее название – экстремумы
функции.
назад
21.
Экстремумы функцииymax 4;
ymax 7
ymin 4
22.
Наибольшее и наименьшее значения функцииyнаим 7
yнаиб 7





















 mathematics
mathematics








