Similar presentations:
Элементы линейной алгебры
1. РАЗДЕЛ 1 Элементы линейной алгебры
2. Линейная алгебра. Основные сведения о матрицах. Виды и свойства матриц. Операции над матрицами.
3. 1. Понятие матрицы
Определение. Прямоугольная таблица чисел,содержащая т строк и п столбцов, называется
матрицей размера тхп.
Числа, составляющие матрицу – элементы
матрицы. Элементы, стоящие на диагонали,
идущей из верхнего угла, образуют главную
диагональ.
Матрицы обозначаются заглавными буквами
латинского алфавита (А, В, С, …), а элементы
матрицы – строчными буквами с двойной
индексацией ( a i j , где i – номер строки,
j – номер столбца).
Матрицы записываются ( ), или [ ], или || ||.
4.
илиa11
a21
...
A
m n
ai1
...
a
m1
a12
...
a1 j
...
a22
...
a2 j
...
...
...
...
...
ai 2
...
aij
...
...
...
...
...
am 2
...
amj
...
a1n
a2 n
...
ain
...
amn
или
A ai j , i 1, 2,..., m,
Например,
1 0
A
2 3
2 5
3
8
j 1, 2,..., n.
5.
Определение. Две матрицы А и Водного размера называются равными,
если они совпадают поэлементно, т.е.
А = В, если aij bij для любых
i 1, 2,..., m,
j 1, 2,..., n.
6.
С помощью матриц удобно записывать некоторыеэкономические зависимости.
Например, таблица распределения ресурсов по
отдельным отраслям экономики (усл. ед.):
Ресурсы
Электроэнергия
Трудовые ресурсы
Водные ресурсы
Отрасли экономики
промышленность
сельское хозяйство
5,3
2,8
4,8
4,1
2,1
5,1
5,3 4,1
A
2
,
8
2
,
1
может быть записана в виде матрицы
3 2
4,8 5,1
Например, элемент a11 5,3 показывает, сколько электроэнергии
потребляет промышленность, а элемент a22 2,1 – сколько трудовых
ресурсов потребляет сельское хозяйство.
7. 2. Виды матриц
Определение. Матрица, состоящая из однойстроки, называется матрицей (вектором)строкой, а из одного столбца – матрицейстолбцом:
A a11 a12 ... a1n – матрица-строка
1 n
b11
b21
B – матрица-столбец
m 1
...
b
m1
8.
Определение. Если число столбцовматрицы п равно числу ее строк, то
матрицу называют квадратной п-го
порядка.
Ее элементы a11, a22 ,..., ann
главную диагональ матрицы.
Например,
образуют
– квадратные матрицы 3-го порядка.
9.
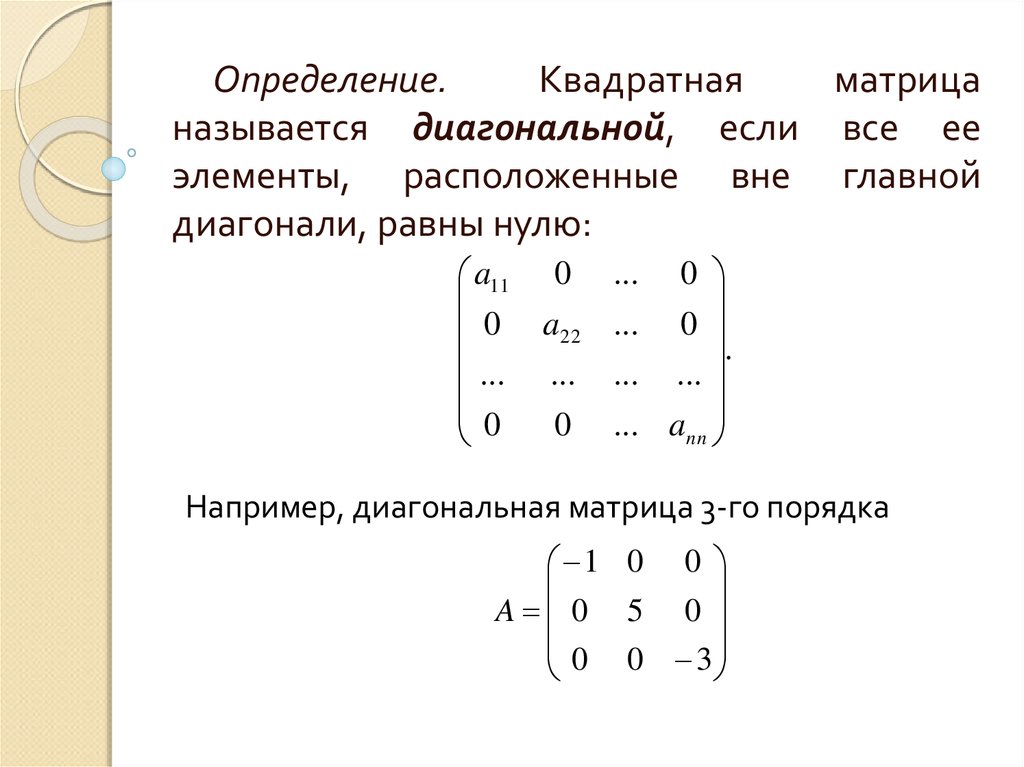
Определение.Квадратная
матрица
называется диагональной, если все ее
элементы, расположенные вне главной
диагонали, равны нулю:
a11 0
0 a22
... ...
0
0
0
... 0
.
... ...
... ann
...
Например, диагональная матрица 3-го порядка
1 0 0
A 0 5 0
0 0 3
10.
Если у диагональной матрицы п-го порядкавсе диагональные элементы равны единице,
то матрица называется единичной п-го
порядка и обозначается буквой Е:
1
0
E
...
0
0 ... 0
1 ... 0
... ... ...
0 ... 1
Например, единичная матрица 3-го порядка имеет вид
1 0 0
E 0 1 0
0 0 1
11.
Определение.Матрица любого размера называется
нулевой или нуль – матрицей, если все ее
элементы равны нулю:
0
0
O
m n
...
0
0 ... 0
0 ... 0
... ... ...
0 ... 0
12. Определение.
Квадратнаяматрица
называется
треугольной, если все ее элементы,
расположенные по одну сторону от главной
диагонали, равны нулю.
Например,
0
1 0
0 ,
2 5
3 1 3
1 2 3
0 5 1
0 0 3
13. 3. Операции над матрицами
1) Умножение матрицы на число.Определение. Произведением матрицы А на
число λ называется матрица В=λА, элементы
которой bij aij для i 1, 2,..., m, j 1, 2,..., n.
Правило. Чтобы умножить матрицу на число, надо
каждый элемент матрицы умножить на это число:
a11
a21
...
a
m1
a12
a22
...
am 2
... a1n a11 a12
... a2 n a21 a22
... ...
...
...
... amn am1 am 2
... a1n
... a2 n
... ...
... amn
14.
Например,10 20
2 4
Если A
.
, то 5A
15 10
3 2
Следствие. Общий множитель всех
элементов матрицы можно выносить за знак
матрицы.
20 12 6 10 6 3
Например,
2
.
52 2 0 26 1 0
Частный случай: произведение матрицы
на число 0 есть нулевая матрица, т.е.0 A O
15. 2) Сложение матриц
Определение. Суммой матриц А и Водинакового размера называется матрица
С = А + В, элементы которой равны суммам
элементов матриц А и В, расположенных на
соответствующих местах, т.е. матрицы
складываются поэлементно:
cij aij bij для i 1, 2,..., m, j 1, 2,..., n.
a11 ... a1n b11 ... b1n a11 b11 ... a1n b1n
A B ... ... ... ... ... ... ...
...
...
a
m1 ... amn bm1 ... bmn am1 bm1 ... amn bmn
16.
Например,2 3 0
0 1 4
, B
,
если A
1 5 6
2 5 1
2 4 4
то C A B
3 10 7
Частный случай:
А + О = А.
17. 3) Вычитание матриц
Определение. Разность двух матрицодинакового размера определяется через
предыдущие операции:
А – В = А + (−1) ∙ В.
Например,
2 3 0
0 1 4
, B
,
если A
1 5 6
2 5 1
2 2 4
то A B
1 0 5
18. 4) Умножение матриц.
Матрицу А можно умножить на матрицу Втолько в том случае, когда число столбцов
матрицы А равно числу строк матрицы В.
В результате умножения получится матрица
С, у которой столько же строк, сколько их в
матрице А, и столько же столбцов, сколько их
в матрице В, т.е.
A m n B n k C m k
19.
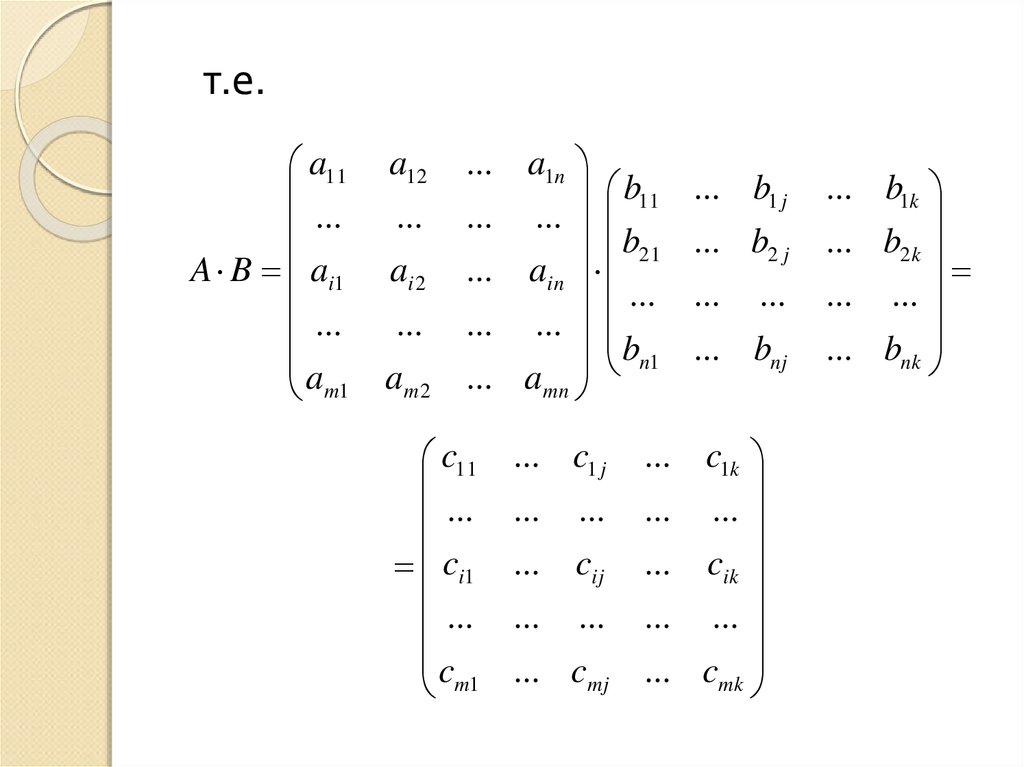
т.е.a11
...
A B ai1
...
am1
a12
...
ai 2
...
am 2
... a1n
b11
... ...
b21
... ain
...
... ...
bn1
... amn
c11
...
ci1
...
c
m1
... c1 j
...
...
...
cij
...
...
... cmj
... b1 j
... b2 j
...
...
... bnj
... c1k
... ...
... cik
... ...
... cmk
... b1k
... b2 k
... ...
... bnk
20.
Элементы матрицы С вычисляются поформуле:
c a b a b ... a b ,
ij
i1
1j
i2
2j
in
nj
т.е. каждый элемент cij равен сумме
произведений элементов i-й строки матрицы
А на соответствующие элементы j-го столбца
матрицы В.
Правило. Для получения элемента , надо
элементы i-й строки матрицы А умножить на
соответствующие элементы j-го столбца матрицы
В и полученные произведения сложить .
21. Пример.
Вычислить произведение матриц А ∙ В, где1 0 1
1 0 2
, B 5 1 4 .
A
3 1 0
2 0 1
Найдем размер матрицы-произведения A B C
2 3 3 3
2 3
1 1 0 5 2 2 1 0 0 1 2 0 1 1 0 4 2 1
C
3 1 1 5 0 2 3 0 1 1 0 0 3 1 1 4 0 1
5 0 3
C
2 1 7
22. 5) Возведение в степень
Определение. Целой положительнойстепенью Ат (т>1) только квадратной
матрицы А называется произведение т
матриц, равных А, т.е.
A
A
A
...
A
m
m
ðàç
По определению:
A E; A A;
0
1
A
m k
Amk ; Am Ak Am k .
23. Пример.
Возвести матрицу A в квадрат и в куб,1 2
A
3 4
Решение.
1 2 1 2 1 1 2 3 1 2 2 4 7 10
A
3 4 3 4 3 1 4 3 3 2 4 4 15 22
2
7 10 1 2 7 1 10 3 7 2 10 4 37 54
A A A
15 22 3 4 15 1 22 3 15 2 22 4 81 118
3
2
24. 6) Транспонирование матрицы -
переход от матрицы А к матрице A AT , вкоторой строки и столбцы поменялись
местами с сохранением порядка.
A AT называется транспонированной
Матрица
относительно матрицы А:
a11
a21
A
m n
...
a
m1
a12
a22
...
am 2
... a1n
... a2 n
,
... ...
... amn
a11
a12
T
A
n m
...
a
1n
a21 ... am1
a22 ... am 2
.
... ... ...
a2 n ... amn
25.
Например,1 4
1 2 3
, то A 2 5 .
если A
4 5 6
3 6
Свойства операции транспонирования:
A
T T
A
A
T T
A
T
A B
A B
T
A B
B A
T
T
T
T
26. 4. Свойства операций над матрицами
Многие свойства, присущие операциям над числами,справедливы и для операций над матрицами:
1. А + В = В + А
2. (А + В) + С = А + (В + С)
3. А (В + С) = АВ +АС
4. (А + В) С = АС + ВС
5. А (В ∙ С) = (АВ) ∙ С
6. А + О = А
7. А – А = О
8.
9.
A B A B
A B A B A B
27.
Однако имеются и специфическиесвойства матриц.
1) Если
произведение матриц А∙В
существует, то после перестановки
сомножителей местами произведение
матриц В∙А может и не существовать.
Например, A B C существует,
2 3 3 3
2 3
а 3B 3 2A 3 не существует.
28.
2) Если даже произведения А∙В и В∙Асуществуют, то они могут быть
матрицами разных размеров.
Пример. Найти произведение матриц А∙В и В∙А :
0 3
2 1 1
, B 1 5
A
0 3 2
1 1
2 0 1 1 1 1 2 3 1 5 1 1 0 12
A B C
2 3 3 2
2 2
0 0 3 1 2 1 0 3 3 5 2 1 1 17
0 3
0 9 6
2 1 1
2 16 11 , т.е. AB BA
B A D 1 5
3 2 2 3
3 3
1 1 0 3 2 2 2 1
29.
3) Когда оба произведения А∙В и В∙Асуществуют и оба – матрицы одинакового
размера, коммутативный (переместительный)
закон умножения, вообще, не выполняется,
т.е. A B B A .
Пример. Найти произведение матриц А∙В и В∙А , где
1 2
0 5
, B
.
A
3 4
6 8
Решение.
1 2 0 5 12 21
A B
3 4 6 8 24 47
0 5 1 2 15 20
, т.е. AB BA
B A
6 8 3 4 30 44
30.
Частный случай. Коммутативнымзаконом обладает произведение любой
квадратной матрицы А п-го порядка на
единичную матрицу того же порядка,
причем это произведение равно А:
A E E A A
Т.о.,
единичная
матрица
при
умножении играет ту же роль, что и
число 1 при умножении чисел.
31.
4)Произведение двух ненулевых
матриц может равняться нулевой
матрице, т.е. из того, что А∙В = О, не
следует, что А=О или В=О.
Например,
1 1
O ,
A
1 1
1 1
O,
B
1 1
0 0
O
íî
A B
0 0
32. САМОСТОЯТЕЛЬНАЯ РАБОТА №1
Даны матрицы1
1
A N
4
2 N
2
0
2
1 2 N
B 1 0 4
5 1 N
33. Найти: 1) 2А-5В; 2) АВ; 3) ВА; 4) АВ+ВА; 5)
2 ТA
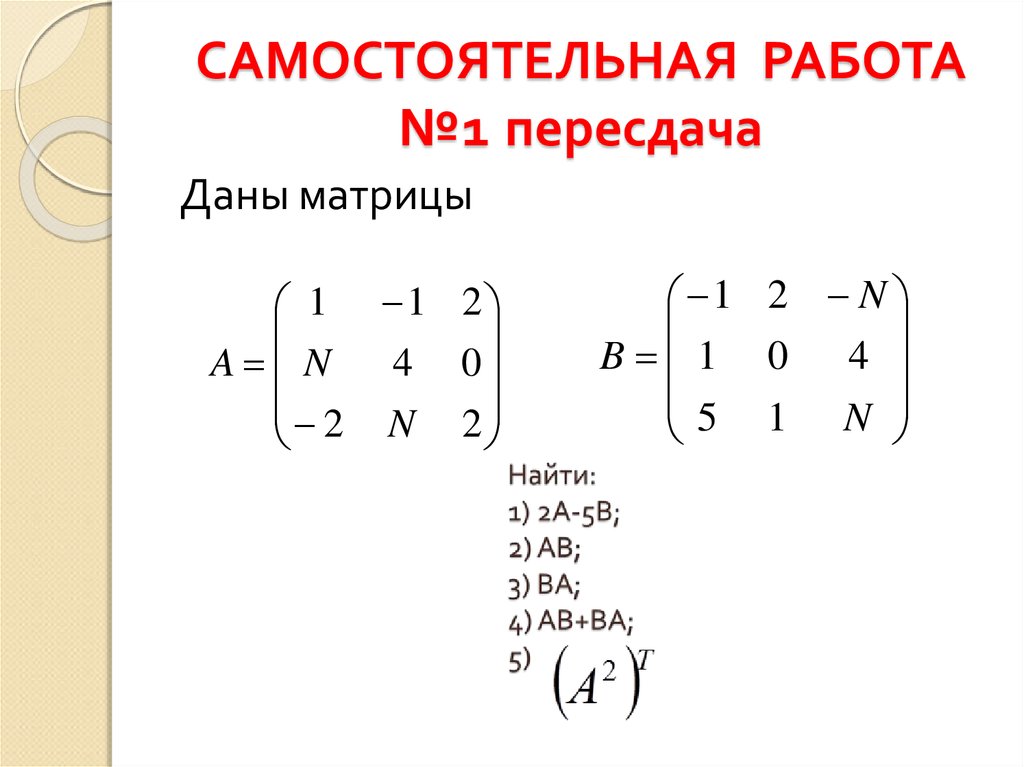
34. САМОСТОЯТЕЛЬНАЯ РАБОТА №1 пересдача
Даны матрицы1 1 2
A N
4 0
2 N 2
1 2 N
B 1 0 4
5 1 N






























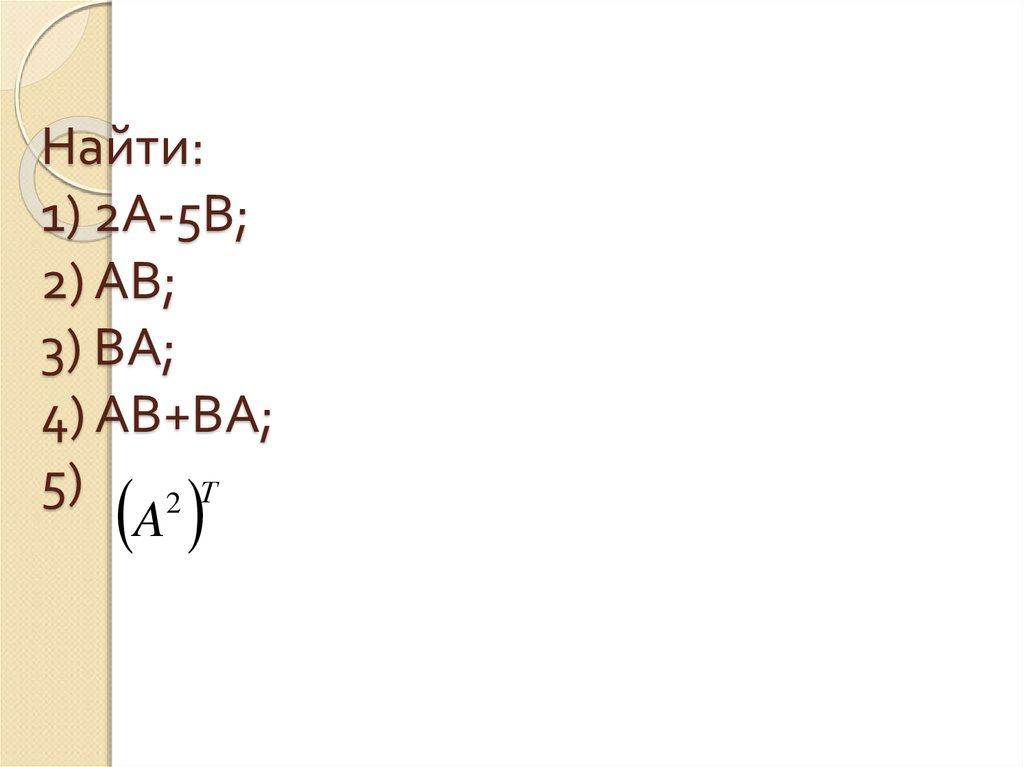
 mathematics
mathematics








