Similar presentations:
Расчет ж/б элементов по предельным состояниям II-ой группы
1. Лекция №9
Расчет ж/б элементов попредельным состояниям
ой группы
II-
2.
Вопросы подлежащие изучению:Общие сведения о расчете.
Определение момента образования трещин.
Расчет ширины раскрытия трещин, нормальных к
продольной силе.
4. Определение прогибов ж/б элементов.
5. Определение кривизны ж/б элементов.
1.
2.
3.
3. 1. Общие сведения о расчете
II-ая группа предельных состояний включает расчеты:1) по образованию и раскрытию трещин;
2) по определению ширины раскрытия трещин, нормальных (┴) к продольной оси;
3) расчеты по прогибам.
В обычных ж/б конструкциях трещины допускаются,
но раскрытие их (ширина) нормируется по следующим
признакам:
- по продолжительности действия нагрузок;
- по условию сохранения арматуры;
- по условию ограничения проницаемости вовнутрь
конструкции.
Ширина раскрытия трещин допускается:
a 0,1 0,4 мм - в зависимости от вида конструкции, от
условий ее эксплуатации.
crc
4. 2. Определение момента образования трещин
Трещины возникнут, если выполняется неравенство:M M crc ;
М – момент от внешней нагрузки;
Мcrc – момент трещинообразования (момент сопротивления
появлению трещин) без учета
растянутого бетона и с их учетом:
неупругих
деформаций
M crc Rbt, serW ; M crc Rbt, serWp
Rbt, ser – расчетное сопротивление по II-ой группе ПС;
W , W p – упругий и упругопластический моменты сопротивл. сечения;
I red
Wp
– учитывает неупругие деформации растянутого бетона
yt
(зависит от формы поперечного сечения), см. табл.1
I red I I s s I s s s Es / Eb ;
Ired – приведенный момент инерции относительно ЦТ сечения;
yt – расстояние от наиболее растянутого волокна бетона до ЦТ сечения.
Ired, W p , yt – рассчитываются по формулам сопромата.
5.
Таблица 1Значения коэффициентов при расчете момента
образования трещин
6. 3. Расчет ширины раскрытия трещин, нормальных к продольной оси
Расчет по раскрытию трещин производится из условия:acrc acrc,ult ; «ultimate» - предельная;
где acrc - ширина раскрытия трещины от внешней нагрузки;
acrc , ult - предельно допустимая ширина раскрытия трещины;
acrc 1 2 3 s
s
s
crc ,
Es
- учитывает работу арматуры между трещинами, зависит от прочности
сцепления бетона с арматурой, от напряжения в арматуре s и т.п.;
1 - коэффициент, учитывающий продолжительность действия нагрузки;
2 - коэффициент, учитывающий профиль продольной арматуры;
3 - коэффициент, учитывающий характер нагружения.
s- напряжение в растянутой арматуре в трещине;
crc - шаг трещин.
7.
sM
;
zs As
s 1 0,8
M crc
;
M
crc 0,5
( s 0,2) - для изгибаемых элементов;
Abt
ds.
As
Расчет по раскрытию трещин не производят, если
соблюдается условие:
M M crc .
8.
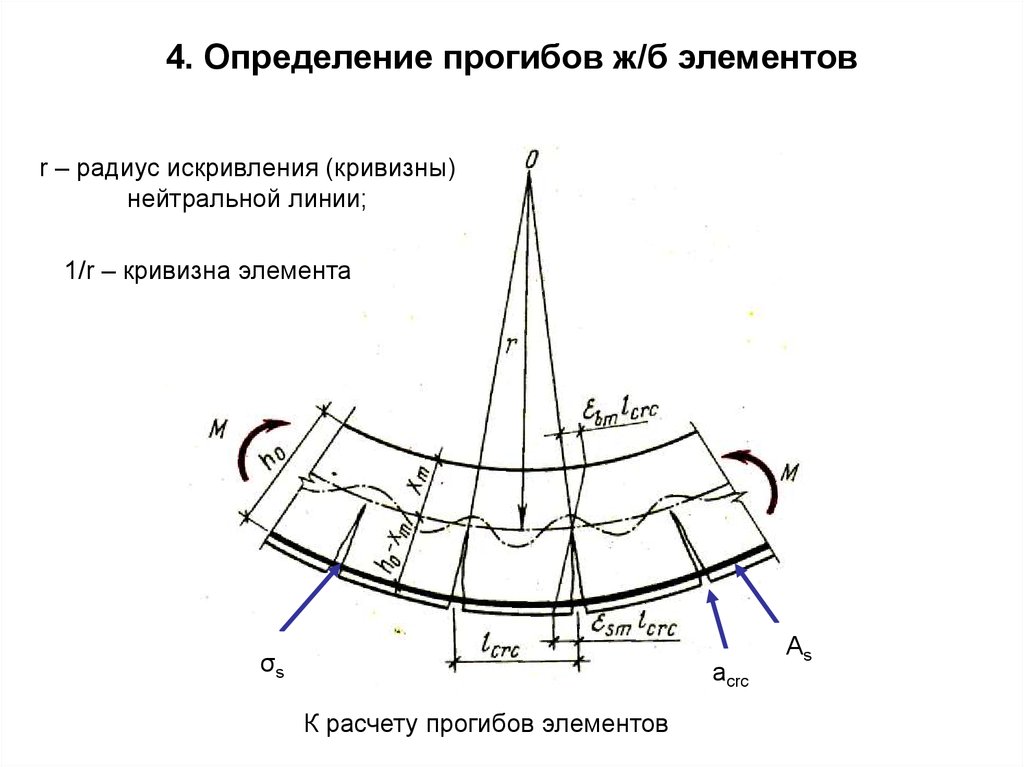
4. Определение прогибов ж/б элементовcrc
r – радиус искривления (кривизны)
нейтральной линии;
1/r – кривизна элемента
σs
acrc
К расчету прогибов элементов
As
9.
Расчет по прогибам производится из условия:f f ult ;
f - прогиб элемента от внешней нагрузки;
f ult - предельно допустимый прогиб элемента по нормам.
Формула для прогиба, обусловленного деформацией
изгиба, имеет вид:
1
f M x ( ) x dx (1)
0
r
где Мх – изгибающий момент от внешней нагрузки в сечении х
Сопротивление конструкции прогибам определяется ее
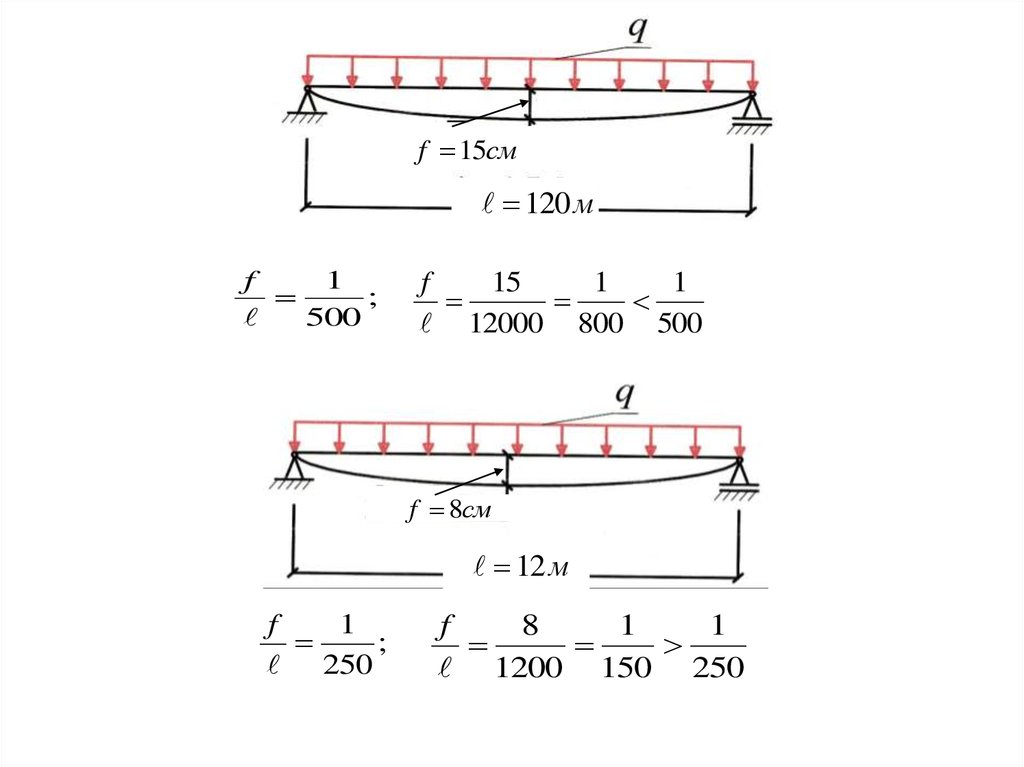
изгибной жесткостью. Жесткость оценивается отношением
f
для конструкций:
1
1
для
гражд
.
здания
от пролета ;
150
250
f
1
1
для пром. зд. или спец . соор.
от пролета.
300
500
10.
f 15см120 м
f
1
;
500
f
15
1
1
12000 800 500
f 8см
12 м
f
1
;
250
f
8
1
1
1200 150 250
11.
Если разбивать элемент на ряд участков, можнополучать прогибы для середин этих участков, используя
формулу (1).
Максимальный прогиб однопролетных свободно
опертых или консольных балок постоянного сечения,
имеющих трещины на каждом участке, рассчитывается по
следующей формуле:
1
f s
r
2
s - характеристика, учитывающая вид нагрузки;
1 - полная кривизна элемента в сечении с наибольшим М.
r
12.
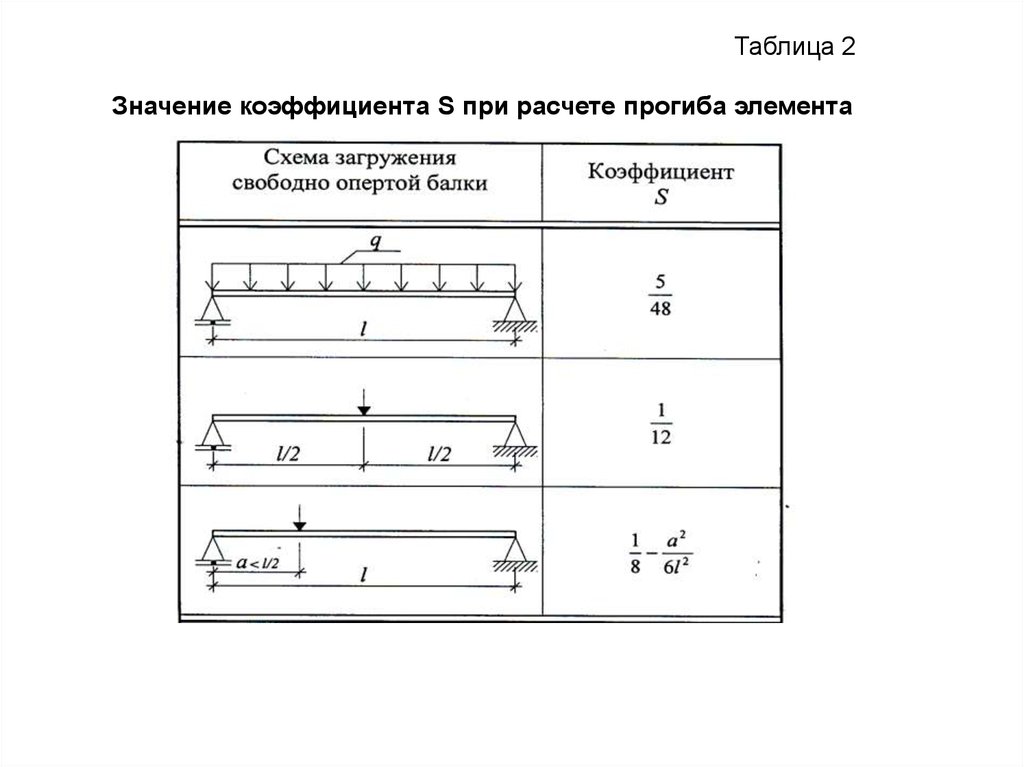
Таблица 2Значение коэффициента S при расчете прогиба элемента
13.
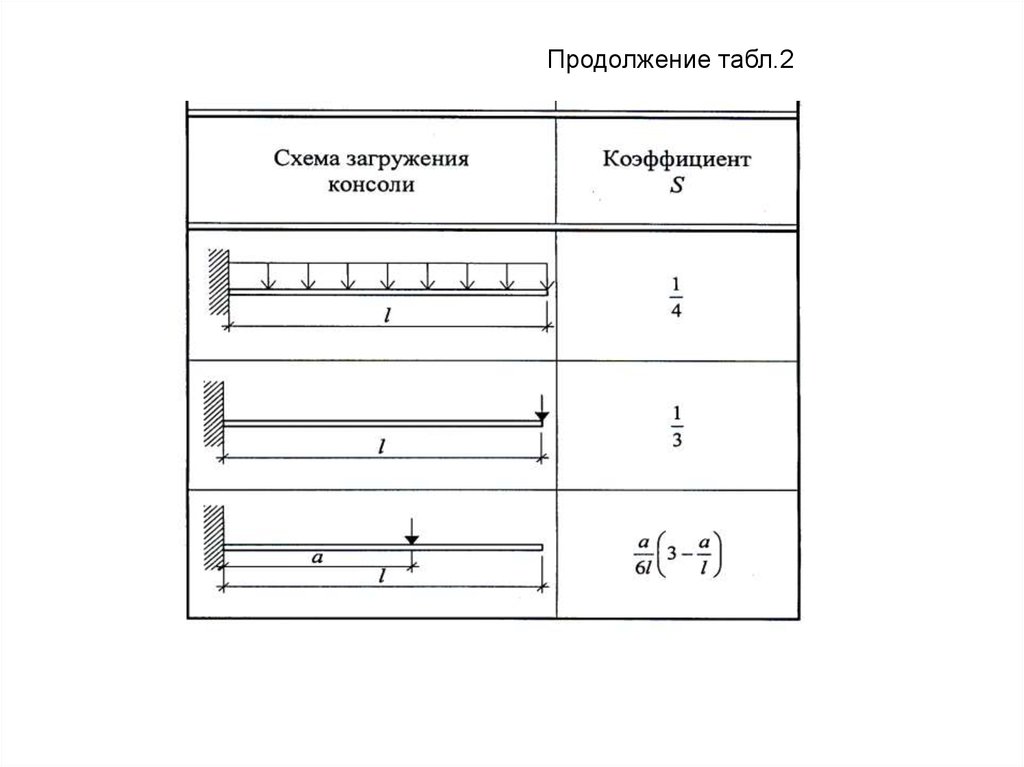
Продолжение табл.214. 5. Определение кривизны ж/б элементов
Различают 2 случая:1) элементы работают без трещин
1
M
r Eb1 I red
Eb1 0,85Eb кратковременное нагружение;
;
Eb
Eb1
длительное нагружение;
1
b ,cr
E b1 - модуль деформации бетона сжатой части;
b,cr - коэффициент ползучести бетона.
2) элементы работают с трещинами
1
M
E b, red - приведенный модуль деформации
r Eb, red I red
сжатого бетона, определяется по СНиП.
Для изгибаемых элементов прямоугольного, таврового и
двутаврового сечения кривизна на участке с трещинами
2
1 M 2bh Rbt,ser
r
1Es As h02
1 , 2 - табличные
коэффициенты для
симметричных сечений
15.
ЗадачаИспользуется принцип независимости
действия сил
M Ne 0
(1 2)%
N M
R s - для металла
A W
M Rbbx(h0 0,5x) ( Rsс As
N
)(h0 a )
2
N M
R д
A W
I 2bh 3 bh 2
W
z 12h
6
- для железобетона
- для дерева











 Construction
Construction








