Similar presentations:
Расчет прогибов железобетонных элементов. (Тема 15)
1. Расчет прогибов железобетонных элементов.
Тема 15Расчет прогибов железобетонных элементов.
f3 – прогиб длительного действия
постоянных и длительных нагрузок;
f4 – прогиб от воздействия ползучести
бетона;
f2 – прогиб от кратковременного
действия постоянных и длительных
нагрузок;
f1 – прогиб от кратковременного
действия полной нагрузки нагрузки;
По формулам строительной механики значение прогиба от изгиба определяется по формуле:
l
1
f M x dx
r x
0
где
M x – изгибающий момент в сечении x от действия единичной силы, приложенной в
сечении, для которого определяется прогиб;
(1/r)x – полная кривизна элемента в сечении x от внешней нагрузки, при которой
определяют прогиб.
2.
Порядок расчета:1. Элемент разбивается на ряд участков.
2. В пределах участка изменение кривизны принимается линейным.
3.
Определяется кривизна по их концам (с учетом наличия трещин).
4. Затем перемножается эпюра моментов и эпюра (1/r) по длине элемента.
3.
В этом случае прогиб в середине пролета будет определяться путем перемноженияэпюр по формуле Верещагина. Тогда:
n
1
2
1
l
1
1
1
1
f
6 i 3 n 2
2
12 n r sup,l r sup,r
r c
i 1
r i ,l r i ,r
где
(1/r)sup,l и (1/r)sup,r – кривизна соответственно на левой и правой опорах;
(1/r)i,l и (1/r)i,r
– кривизна элемента в симметрично расположенных сечениях i и i’,
расположенных слева и справа от оси симметрии.
(1/r)sup,с
– кривизна в середине пролета;
n
– четное число участков разбиения пролета (не меньше 6);
l
– пролет элемента.
4.
Для свободно опертых и консольных элементов прогиб определяется по формуле1
f S l2
r max
(1/r) max - кривизна в сечении с наибольшим изгибающим моментом;
S – коэффициент, зависящий от условий опирания.
5.
При загружении элемента сразу по нескольким схемамS M
S
M
i
i
i
где Si и Mi – коэффициент и величина момента на опоре или в середине пролета от
каждого нагружения.
В этом случае величина (1/r) max определяется для величины момента, равной Mi.
6.
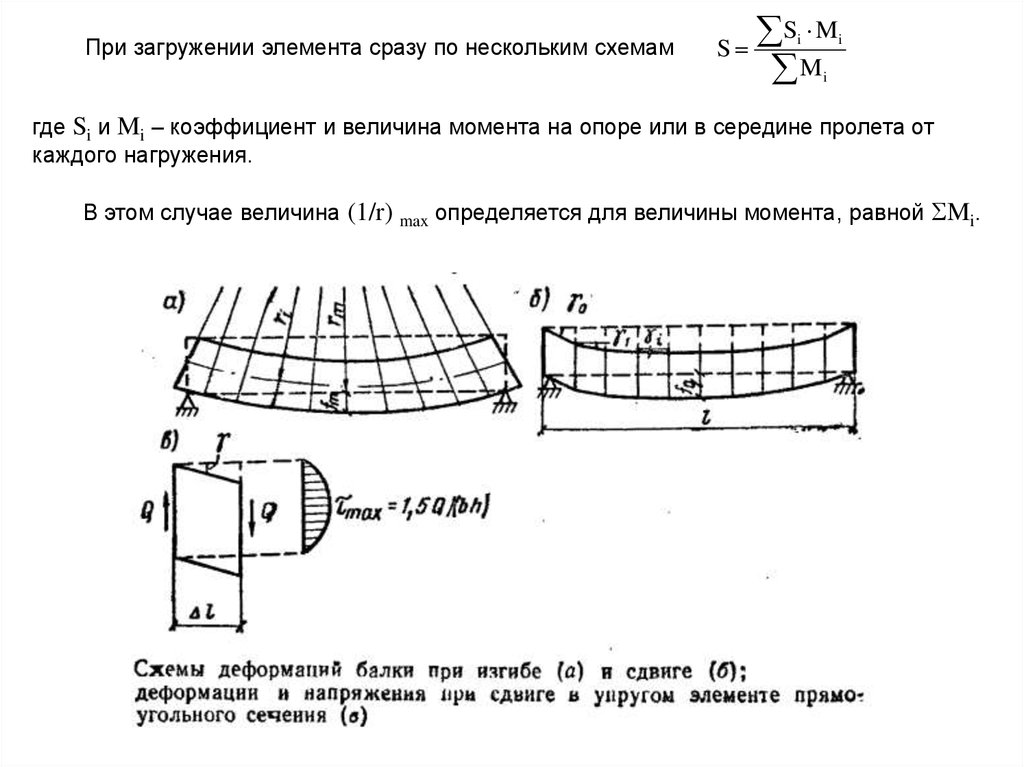
Для изгибаемых элементов при l/h < 10 необходимо учитывать влияние поперечныхсил на прогиб.
В этом случае прогиб будет равен сумме прогибов от изгиба и от сдвига fq.
l
f Qx x dx
0
Qx – поперечная сила в сечении от действия внешней нагрузки, при которой определяется
прогиб.
x – угол сдвига элемента в сечении от действия внешней нагрузки.
Для элементов без трещин величина x определяется по формулам строительной
механики:
x
G
1.5 Qx S red
b I red
7.
Так как эпюра касательных напряжений по высоте сечения не постоянна, то болееточно:
1.2 Qx
x
b G h
При наличии трещин угловые перемещения увеличиваются:
x
1.2 Qx
b crc
G b h
b – коэффициент, учитывающий влияние ползучести бетона и принимаемый равным:
• при длительном действии нагрузок: b = 1 + b,crc;
• при непродолжительном действии нагрузки b = 1.
crc – коэффициент, учитывающий влияние трещин не деформации сдвига:
• на участках без трещин crc = 1;
• на участках, где есть только наклонные трещины crc = 4.0;
• на участках, где есть только нормальные или нормальные и наклонные трещины:
crc
3 Eb I red 1
Mx
r x
Образование наклонных трещин проверяется по условию:
Q 0.5 Rbt ,ser b h0






 Construction
Construction








