Спектры землетрясений. Расчёт сооружений на сейсмостойкость

1.

Московский государственный университет путей
сообщения
Спектры землетрясений
Курбацкий Евгений Николаевич
профессор кафедры “Мосты и тоннели”,
д.т.н.

2.

Введение
Спектры реакций (ответов) одна из наиболее
важных, полезных и широко используемых
концепций в теории и практике расчётов сооружений
на сейсмостойкость.
Предложенная более 80-ти лет назад, в настоящее
время эта концепция используется практически во
всех зарубежных нормативных документах и
руководствах
по
расчёту
сооружений
на
сейсмостойкость.

3.

В статье известного американского учёного
А. К. Chopra «Спектр ответа упругих систем.
Исторические заметки» отмечается, что
«концепция спектров ответов хорошо
интегрировалась в теорию и практику
инженерных
расчётов
сооружений
на
сейсмостойкость, но многие исследователи и
инженеры, использующие эту концепцию, не
знают происхождения концепции и добавим
от себя, не понимают физической сущности
этой концепции».

4.

В Российских нормах для оценки сейсмических
воздействий используется понятие «спектральный
коэффициент динамичности»- .
Кривые коэффициента динамичности в
российских нормах строятся как функции периода
свободных колебаний осциллятора. Это практически
та же концепция, названная по-другому.
Почему разработчики Российских норм, знакомые
и использующие эту уже распространенную в ту пору
концепцию (а это были семидесятые годы прошлого
столетия) применили для её представления менее
удачные в данном случае термины «динамические
коэффициенты», остаётся только догадываться.

5.

История появления концепции
Экспериментальные исследования
Впервые идея использования спектров
максимальных реакций для представления
сейсмических воздействий была изложена в
1926 году в бюллетене
Института
исследования землетрясений Императорского
Токийского Университета в статье первого
директора Института K. A. Сюэхиро.

6.

Анализатор сейсмических колебаний
13-ть оссциляторов, с различными собственными
частотами, изменяющимися в диапазоне от 0.55 до
4.5 Гц (с периодами в диапазоне от 0.22 до 1.81 сек).

7.

Основные положения
Определение.
«Спектр ответов - график
максимальных реакций: перемещений, скоростей,
ускорений, или других максимальных параметров
совокупности осцилляторов (систем с одной
степенью свободы) на заданное воздействие.
Ординаты спектра ответов - максимальные
значения реакций осцилляторов на заданное
воздействие, абсцисса спектра - собственные частоты
осцилляторов или периоды собственных колебаний.

8.

Численные методы построения
спектров ответов
С появлением быстродействующих компьютеров
возможности реализации численных методов с
использованием
больших
массивов
чисел
существенно возросли.
Разработке численных методов построения
спектров ответов способствовал и тот факт, что
современные измерительные комплексы позволяют
получать сейсмограммы колебаний поверхности
грунта при землетрясениях в цифровой, удобной для
дальнейшей обработки форме.

9.

Способы построения спектров
ответов с использованием численных
методов, которые легко реализуются
в пакете программ Matlab:
- интеграл Дюамеля
- метод прямого (пошагового) интегрирования,
- -метод Вильсона,
- -метод Ньюмарка,
- метод Рунге – Кутта,
- метод решения с использованием алгоритма
быстрого преобразования Фурье

10.

Для построения спектров максимальных реакций
рассматриваются простейшие механические
системы, динамические свойства которых
определяются тремя параметрами: массой m ,
жёсткостью k и демпфированием c
m
m
с
m
c
k
2
k
2
m
k
2
m
m
с
ug
ug
m
Рис.2 Системы с одной степенью свободы
k
2
ug

11.

Два предельных случая
Масса жёстко прикреплена к колеблющемуся
основанию рис. а)
Масса соединена с основанием очень гибкими
связями рис. б).
m um u g
m um 0
m
m
m
m
а)
c
ug
m
m
б)
k
а) 2
c
m
m
ug
m
k
2
m

12.

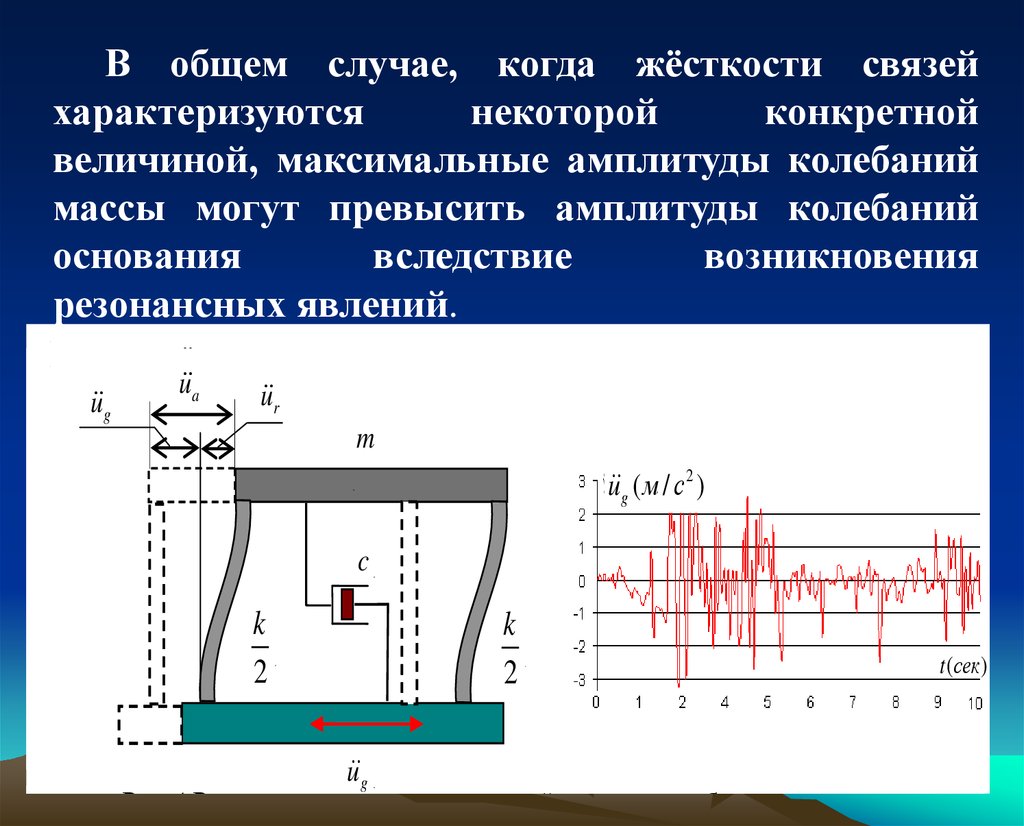
В общем случае, когда жёсткости связей
характеризуются
некоторой
конкретной
величиной, максимальные амплитуды колебаний
массы могут превысить амплитуды колебаний
основания
вследствие
возникновения
резонансных явлений.
c
m
c
m
u&&g
u&&g
u&&a
u&&a
u&&r
u&&r
m
m
u&&g ( м / с 22 )
u&&g ( м / с )
m
m
c
c
k
k
2
2
m
m
k
k
2
2
m
m
m
m
t (сек )
t (сек )
u&&g
u&&g системы с одной степенью свободы и акселерограмма
Рис. 4 Расчётная схема
Рис. 4 Расчётная
схема системы
с одной
степенью(грунта)
свободы и акселерограмма
колебаний
поверхности
основания
m
m

13.

Дифференциальное уравнение
колебаний механической системы
при сейсмическом воздействии
mua ( t ) cur ( t ) kur ( t ) 0
m ug ( t ) ur ( t ) cur ( t ) kur ( t ) 0
mur ( t ) cur ( t ) kur ( t ) mug
ur ( t ) 2 0 ur ( t ) u ( t ) ug
2
0 r

14.

При известном уравнении колебаний грунта
ug (t ) реакция сооружения ur (t ) зависит от
собственной частоты колебаний и
демпфирования
Собственная частота колебаний
конструкции
Коэффициент демпфирования
Ускорение колебаний поверхности
грунта при землетрясении

15.

Кинематическое возбуждение колебаний
системы с собственной частотой колебаний
и коэффициентом демпфирования
Результаты вычислений
зависят от вида функции,
определяющей ускорение, от
частоты собственных колебаний
и коэффициента демпфирования.
При изменении одного из этих
параметров необходимо
выполнять новые расчёты.
Перемещение (м)
Ускорение в долях (g)
Колебания системы с одной степенью
свободы при кинематическом
(сейсмическом) воздействии
Результат вычислений:
(график перемещения массы при
кинематическом возмущении)
Пиковое значение перемещений

16.

Пример построения спектра максимальных
реакций
2
0
0.20
Максимальное перемещение U max 0.135 см
0.15
1
Коэффициент демпфирования 0.05 .
0.10
5
0.05
0.00
1
0
-0.05
-0.10
5
-0.15
-0.20
0
.0
0.0
0.5
1
.0
Период (секунды)
.5
1
Время (секунды)
2
.0
Рисунок 1 Уравнения вынужденных колебаний системы, собственный период колебаний которой
Т=0.1 сек
2
0
1
5
1
0
5
.0
.
1.00
0.75
0.50
0.25
0.00
-0.25
-0.50
-0.75
-1.00
0
0.0
0.5
Период
1
1.0
(секунды)
((секунды)
.5
2
.0
Максимальное перемещение U max 0.635 см
Коэффициент демпфирования 0.05
Время
(секунды)
Рисунок 2 Уравнения вынужденных колебаний системы, собственный период колебаний которой
Т=0.2 сек
20
2.00
1.50
1.00
0.50
0.00
-0.50
-1.00
-1.50
-2.00
15
10
5
0.0
0.0
0.5
1.0
Период (секунды)
Период (секунды)
1.5
Максимальное перемещение U max 1.56 см.
Коэффициент демпфирования 0.05 .
2.0
Время (секунды)
Рисунок 3 Уравнения вынужденных колебаний системы, собственный период колебаний которой
Т=0.3 сек

17.

Пример построения спектра максимальных
реакций (продолжение)
20
3.00
2.25
15
Максимальное перемещение U max 2.4 см.
Коэффициент демпфирования 0.05 .
1.50
0.75
10
0.00
-0.75
-1.50
5
-2.25
-3.00
0.0
0.0
0.5
1.0
Период (секунды)
1.5
2.0
Период (секунды)
Время (секунды)
Рисунок 4 Уравнения вынужденных колебаний системы, собственный
период колебаний которой Т=0.4 сек
20
6.00
Максимальное перемещение U max 5.05 см.
4.50
15
Коэффициент демпфирования 0.05 .
3.00
1.50
0.00
10
-1.50
-3.00
-4.50
5
6.00
0.0
0.0
0.5
1.0
Период (секунды)
1.5
2.0
Время (секунды)
Период (секунды)
Рисунок 5 Уравнения вынужденных колебаний системы, собственный
период колебаний которой Т=0.5 сек

18.

0.05
Спектр максимальных перемещений (см) для
систем c коэффициентом демпфирования 0.05
при воздействии Калифорнийского землетрясения
30
27.1
см
25
25.0
см
22.4
см
20
18.4
см
17.2
15
10
см
12.6
см
12.6
см
7.62
см
5
5.05
см
2.40
см
0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
кк (сек 4.0Период собственных колебаний
3.5 сек

19.

Спектры максимальных перемещений для систем
с разными коэффициентами демпфирования
Для учёта демпфирующих свойств конструкций из
различных
строительных
материалов
необходимо
построить
семейство
спектральных
кривых,
с
различными коэффициентами демпфирования:
для
конструкций
из
стали
коэффициент
демпфирования равен 0.02, если уровень напряжений
меньше, чем ½ от напряжений предела текучести,
- для бетона коэффициент демпфирования зависит от
уровня напряжений и находится в пределах: от 0.02 до
0.04,
- для резинометаллических опорных частей этот
коэффициент может меняться в широких пределах: от
0.06 до 0.12 .
Коэффициент демпфирования грунтов зависит от уровня
деформаций и может изменяться в пределах 0.5% - 2%.

20.

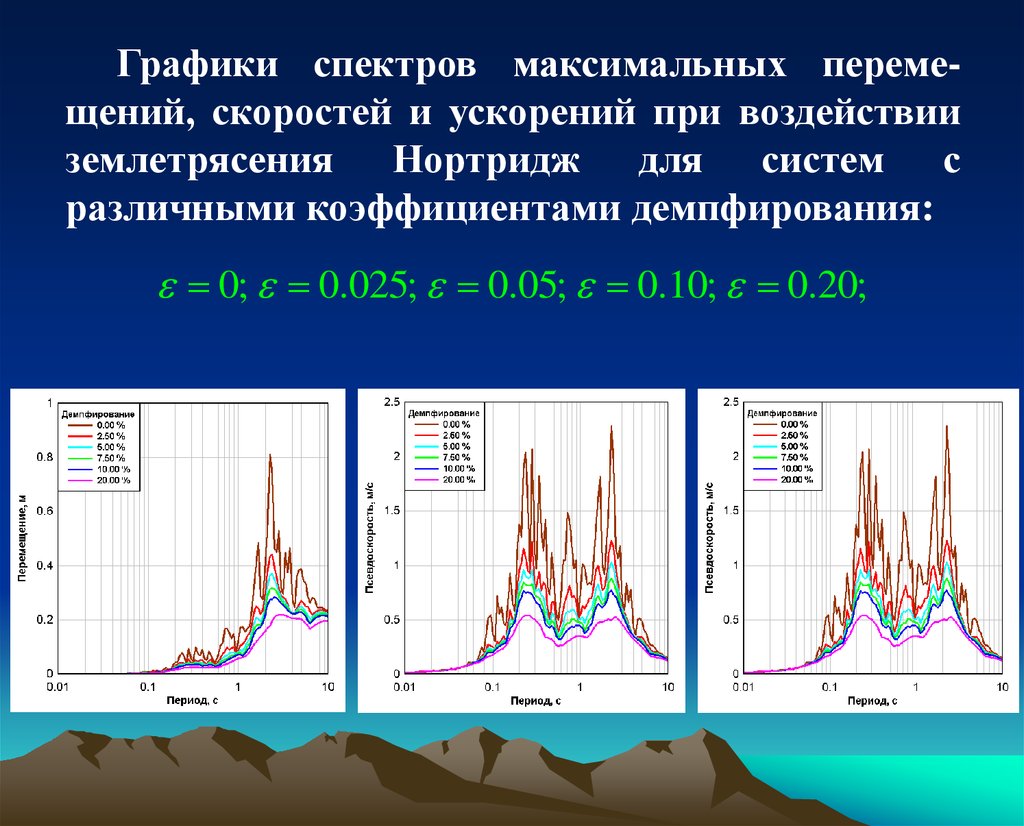
Графики спектров максимальных перемещений, скоростей и ускорений при воздействии
землетрясения Нортридж для систем с
различными коэффициентами демпфирования:
0; 0.025; 0.05; 0.10; 0.20;

21.

Для построения
необходимо решить
уравнение:
спектров ответов
дифференциальное
u (t ) 2 0u (t ) u (t ) u g (t )
2
0
Для
получения
решения
можно
воспользоваться интегралом Дюамеля:
t
1
0 ( t )
u (t )
u
(
)
e
sin (t ) d
g
m 0

22.

Псевдоспектры максимальных перемещений,
скоростей и ускорений
Спектры
максимальных
скоростей
и
спектры
максимальных ускорений могут быть получены таким же
образом, как определялись спектры максимальных
перемещений.
Разница будет заключаться в том, что вместо определения
пиковых значений перемещений необходимо будет
определять пиковые значения скоростей и пиковые
значения ускорений.
Sa ( , ) - спектр максимальных абсолютных ускорений,
Sv ( , )- спектр максимальных относительных скоростей,
Sd ( , ) -
спектр
перемещений.
максимальных
относительных

23.

Вместо этого используют приближённый способ,
полагая, что зависимость спектра перемещений от
времени представляет собой гармоническую
функцию.
В таком случае спектр максимальных скоростей
определяется выражением:
S pv ( , ) Sd ( , )
Спектр
максимальных
определяется выражением:
ускорений
S pa ( , ) S pv ( , ) Sd ( , )
2
S pa ( , ) S pv ( , ) Sd ( , )
2

24.

S pv ( , ) Sd ( , )
S pa ( , )
Можно показать, что для построения
спектров достаточно определить только
спектр псевдоскоростей по формуле:
t
i ( t )
S pv ( , ) u (t )sin (t )e
d
0
max
Для систем с малыми коэффициентами
демпфирования, к которым можно отнести,
практически, большинство строительных
конструкций, справедливы соотношения:
S pv ( , ) Sd ( , )
S pa ( , )

25.

Трёхординатный (tripartite) график
псевдоспектров
Учитывая зависимость:
S pv ( , ) Sd ( , )
S pa ( , )
три графика, а именно: график псевдоспектров
скоростей, график перемещений и график
ускорений, можно совместить в одном.
Прологарифмировав
соотношение, получим:
выше
представленное
lg S pv ( , ) lg Sd ( , ) lg
lg S pv ( , ) lg S pa ( , ) lg

26.

В логарифмических координатах эти
функции имеют вид:
y pd ( x ) y pv ( x ) x
y pa ( x ) y pv ( x ) x
где
x lg ,
y pd ( x ) lg Sd ( , ) ;
y pv lg S pv ( , ) ;
y pa ( x ) lg S pa ( , )

27.

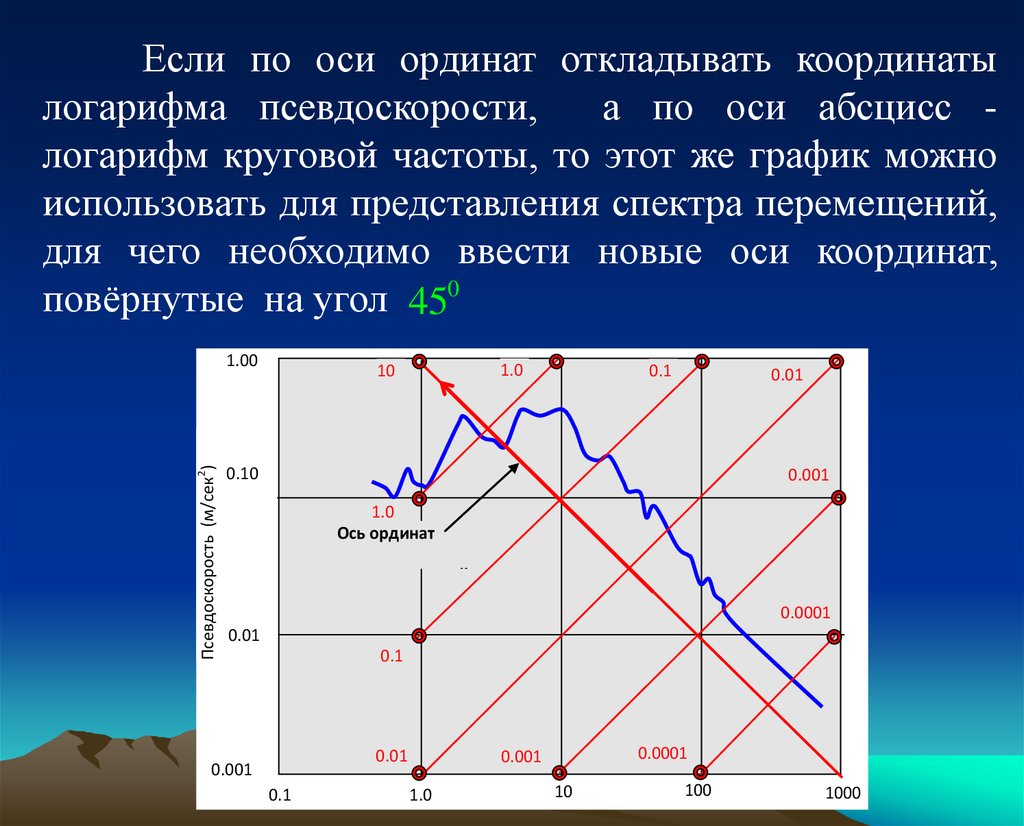
Если по оси ординат откладывать координаты
логарифма псевдоскорости,
а по оси абсцисс логарифм круговой частоты, то этот же график можно
использовать для представления спектра перемещений,
для чего необходимо ввести новые оси координат,
повёрнутые на угол 450
Псевдоскорость (м/сек2)
1.00
1.0
10
0.1
0.01
0.10
0.001
1.0
Ось ординат
псевдоперемещений
0.0001
0.01
0.1
0.01
0.001
0.1
0.0001
0.001
1.0
.4
10
100
1000
8

28.

Для построения графика псевдоускорений,
совмещенного с графиком псевдоскорости,
необходимо добавить оси, повёрнутые на 450
1
1
1
.00
0
Псевдоскорость
(м/сек )
.0
0
.10
1
00
0
2
.1
Ось ординат
Ось
псевдоускорений
ординат
псевдоуско
рений 0
0
.01
1
0
.01
1
0
0
.001
.1
0
.001
0
.1 1
.01 1
Круговая
частота 00
0
(рад/сек)
0
.0
1
1
.0.
4
0008

29.

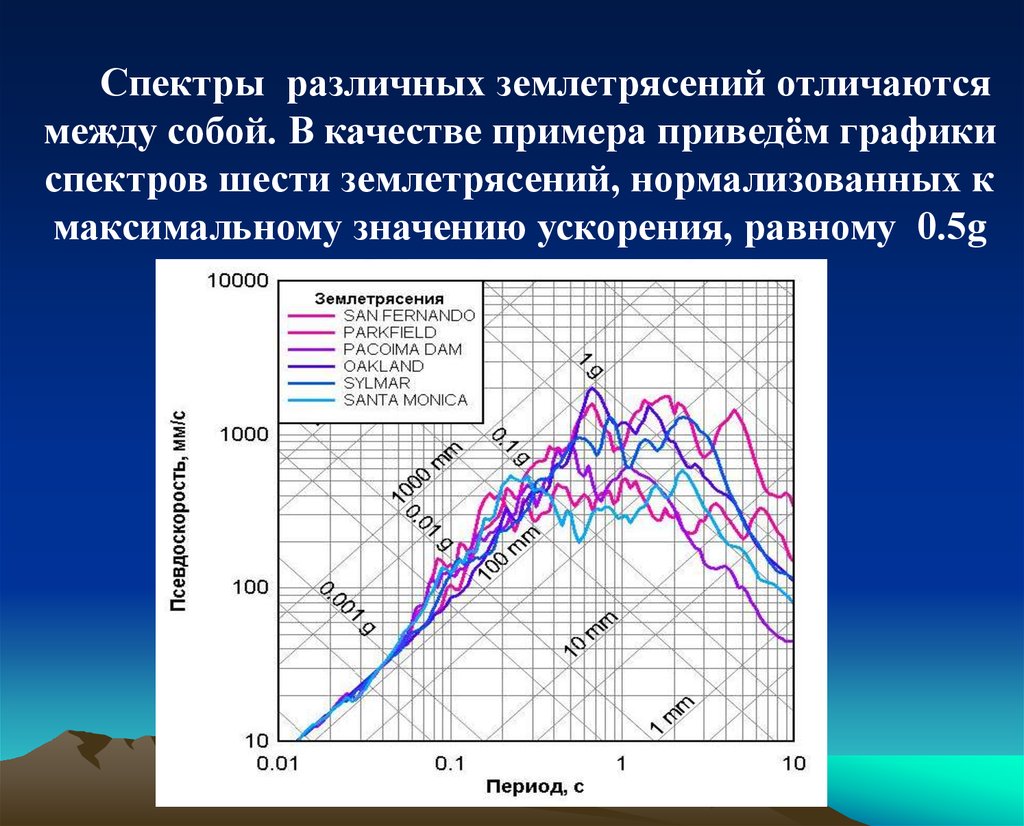
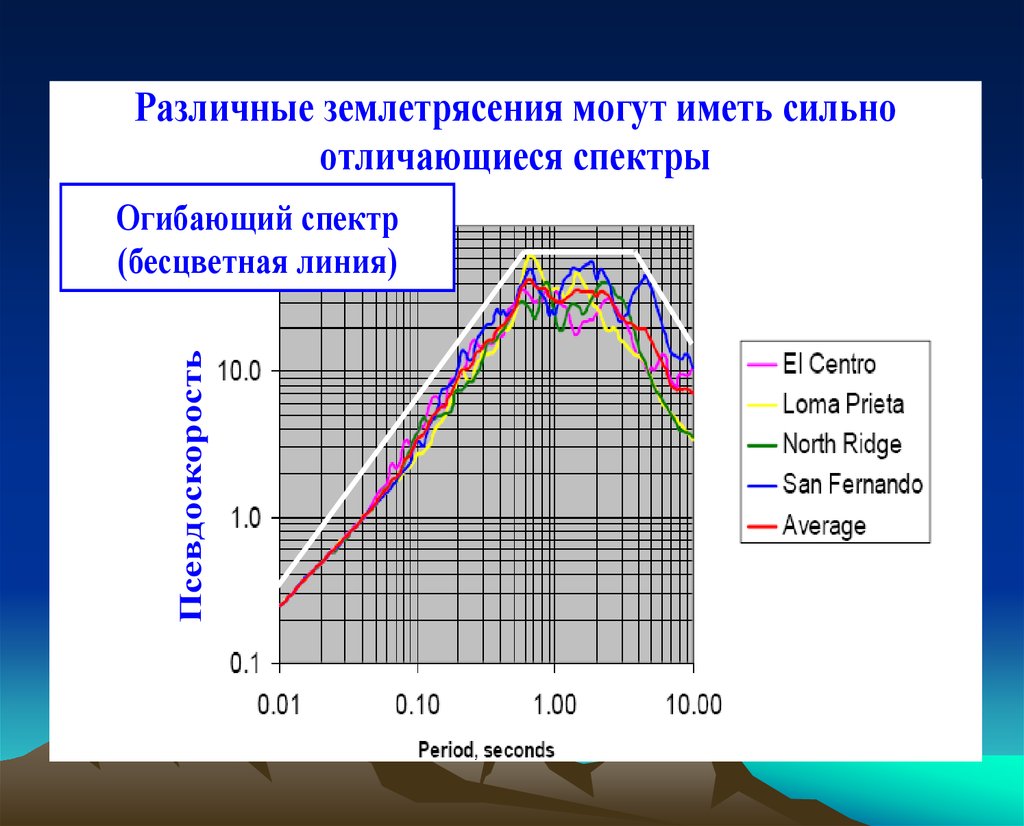
Спектры различных землетрясений отличаются
между собой. В качестве примера приведём графики
спектров шести землетрясений, нормализованных к
максимальному значению ускорения, равному 0.5g

30.

Различные землетрясения могут иметь сильно
отличающиеся спектры
Псевдоскорость
Огибающий спектр
(бесцветная линия)

31.

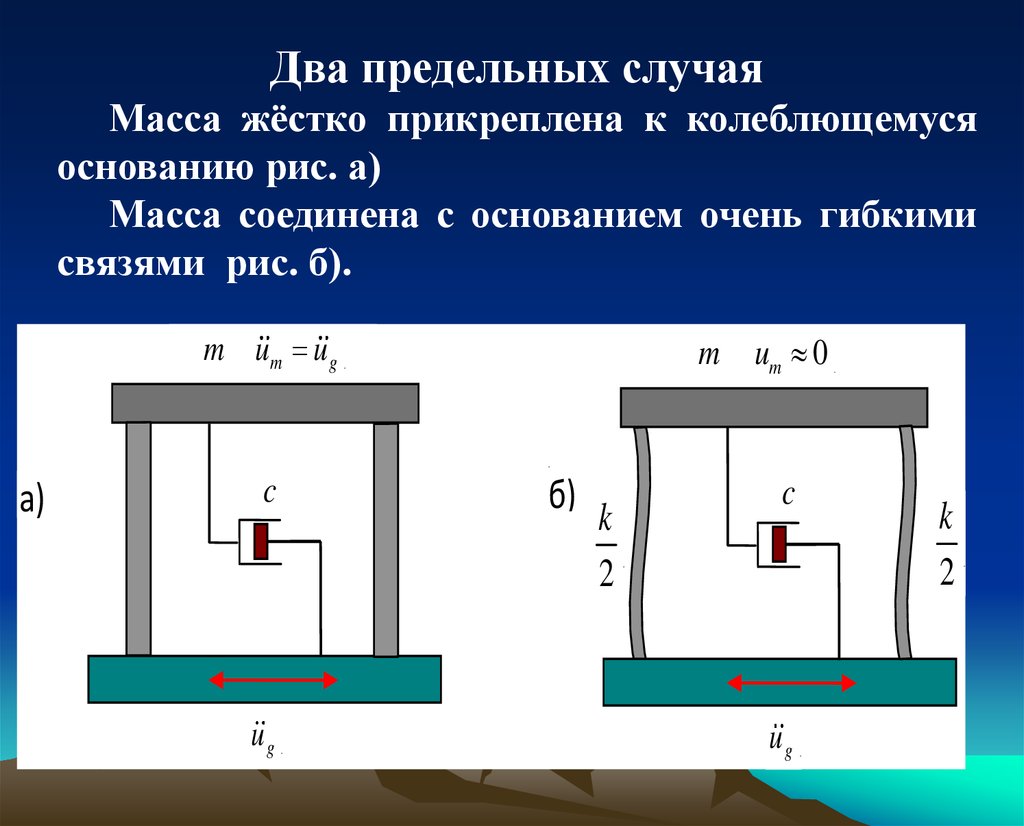
Два предельных случая
Масса жёстко прикреплена к колеблющемуся
основанию рис. а)
Масса соединена с основанием очень гибкими
связями рис. б).
m um u g
m um 0
m
m
m
m
а)
c
ug
m
m
б)
k
а) 2
c
m
m
ug
m
k
2
m

32.

Построение расчётных спектров ответов
В качестве исходных данных используются
пиковые значения ускорений, скоростей и
перемещений
поверхности
грунта
и
коэффициенты
усиления
колебаний
(коэффициенты динамичности):
a ; v ; d
На
основании
статистической
обработки
акселерограмм большого количества землетрясений
были получены соотношения, позволяющие получать
спектры реакций, если известно пиковое значение
ускорений грунта . Рекомендуемые соотношения для
жёстких грунтов имеют следующий вид:
ug / ug 1,2 м / сек / g
ug ug / ug2 6

33.

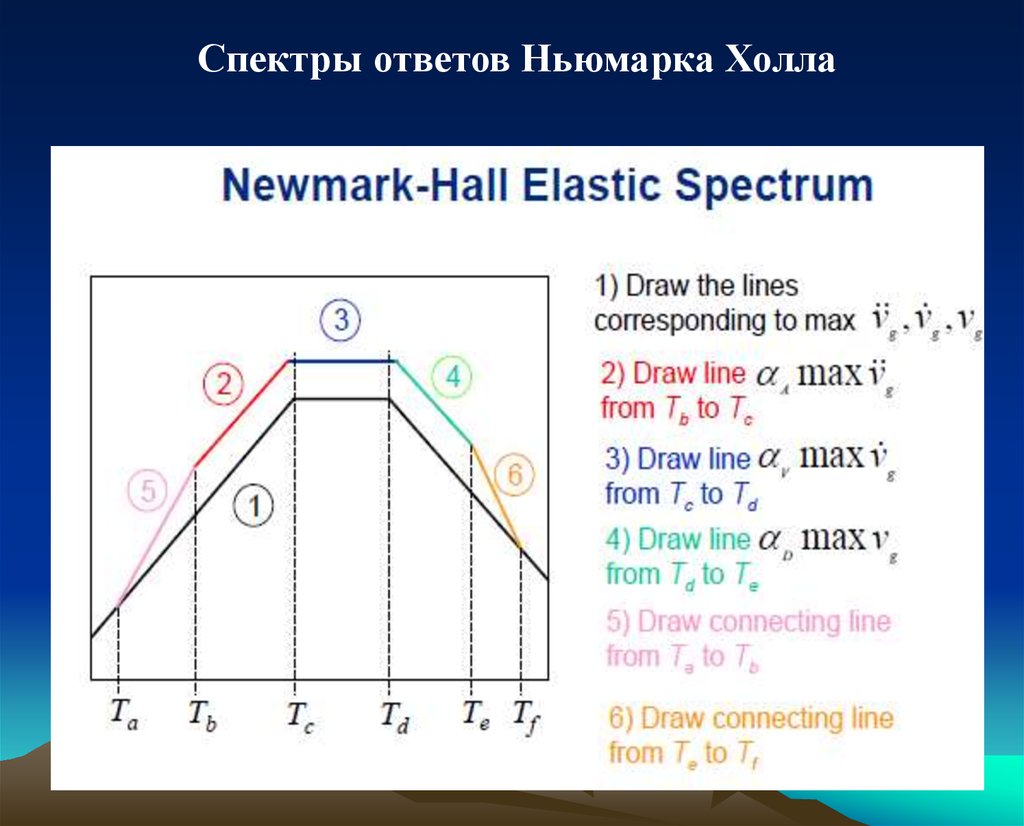
Методика построения спектров Ньюмарка
Холла
Построение спектров Ньюмарка основано на следующих
положениях:
- псевдоускорения при очень малых периодах колебаний
равны пиковым ускорениям грунта;
- относительные перемещения при больших периодах
колебаний равны пиковым перемещениям грунта;
- при промежуточных периодах псевдоскорости считаются
постоянными и определяются значением пикового ускорения,
умноженного на некоторую постоянную величину.
Огибающие спектры повторяют эту конфигурацию за
исключением переходных отрезков прямых.

34.

Спектры ответов Ньюмарка Холла

35.

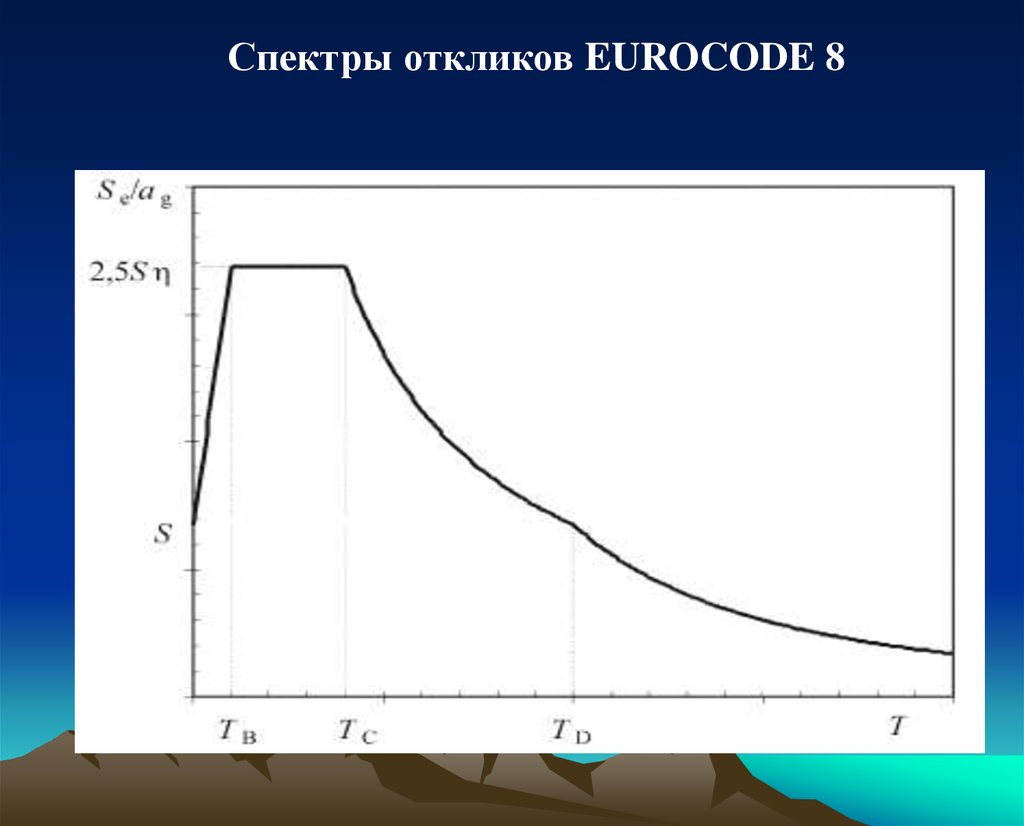
1)
0 ≤ T ≤ TB:
T
S e (T ) a g S 1
( 2,5 1)
TB
S e (T ) a g S 2,5
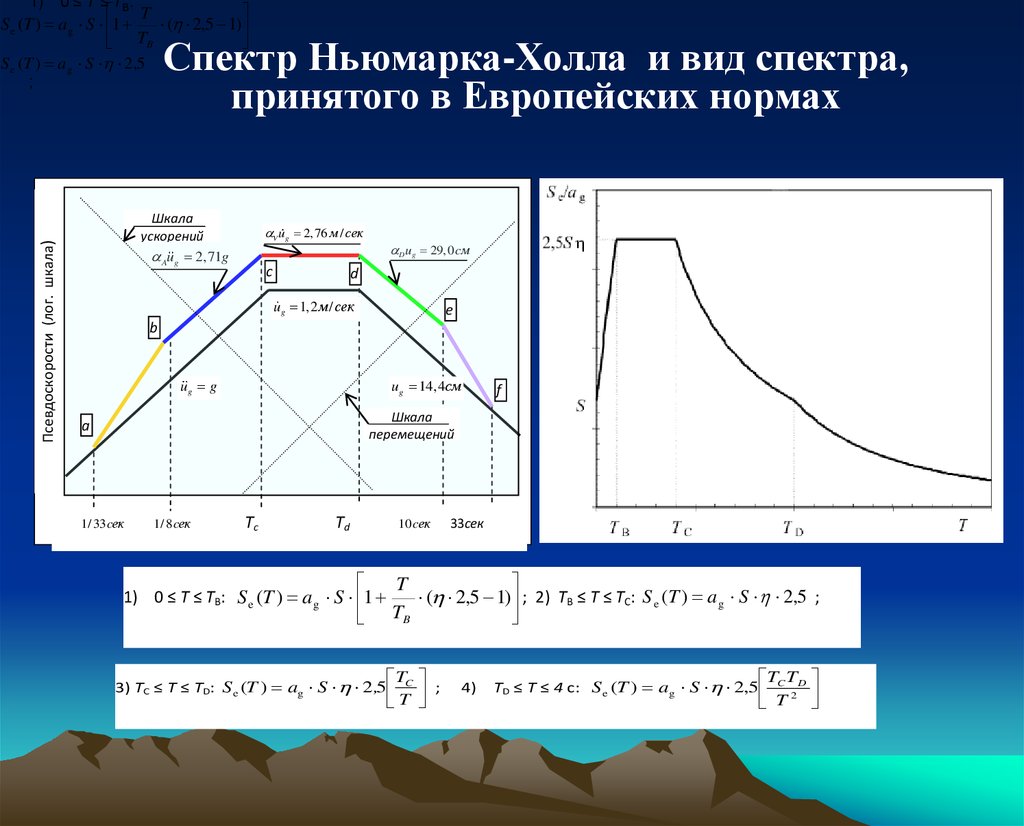
Спектр Ньюмарка-Холла и вид спектра,
принятого в Европейских нормах
Шкала
ускорений
Aug 2,71g
V ug 2, 76 м / сек
c
b
Dug 29, 0 cм
d
b
ug 1,2 м / сек
ug b
e
b
Псев
Псевдоскорости (лог. шкала)
;
ug g
ug 14,4см
f
b
Шкала
перемещений
a
1/ 33cек
1/ 8cек
Tc
Td
10 cек
1) 0 ≤ T ≤ TB: S e (T ) a g S 1
33сек
T
( 2,5 1) ; 2) TB ≤ T ≤ TC: S e (T ) a g S 2,5 ;
TB
TC
;
T
3) TC ≤ T ≤ TD: S e (T ) ag S 2 ,5
4)
TC TD
2
T
TD ≤ T ≤ 4 c: S e (T ) a g S 2,5

36.

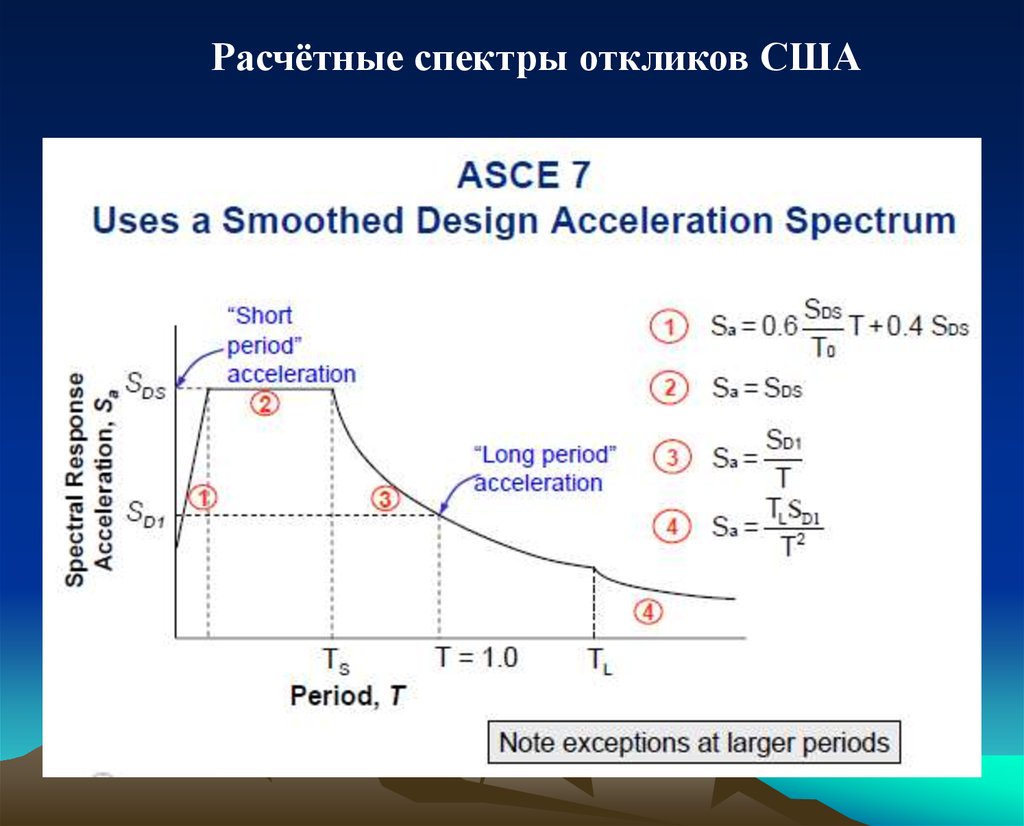
Расчётные спектры откликов США

37.

Спектры откликов EUROCODE 8

38.

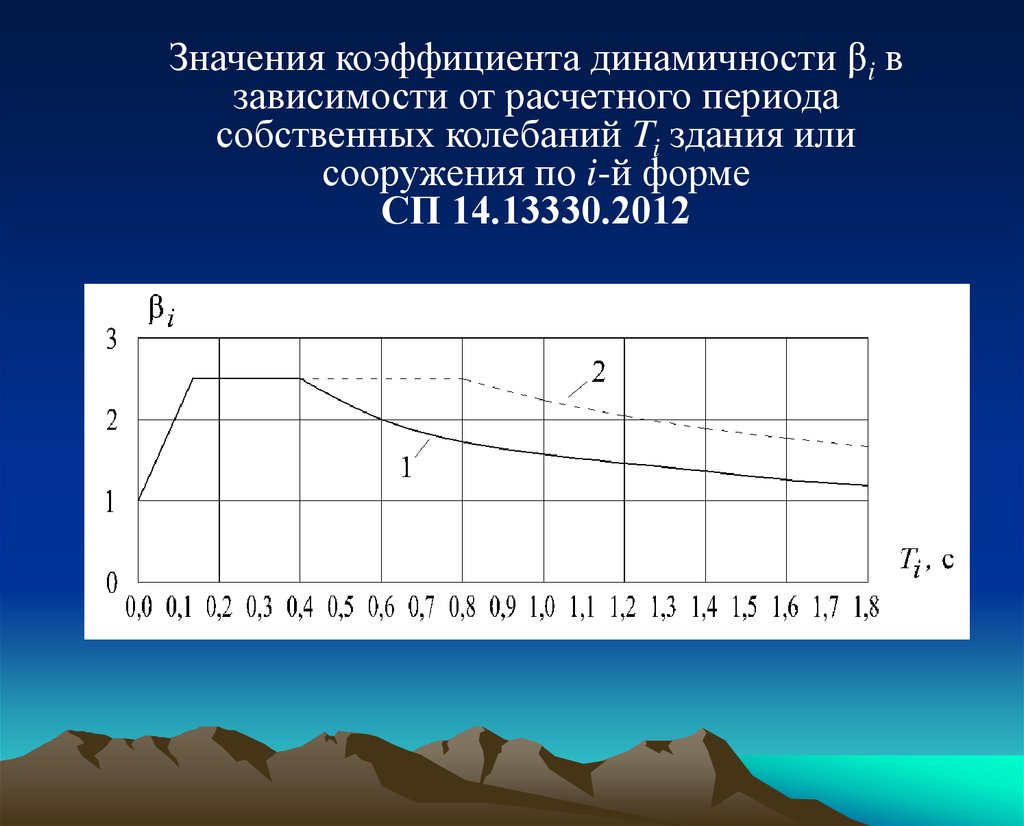
Значения коэффициента динамичности βi в
зависимости от расчетного периода
собственных колебаний Ti здания или
сооружения по i-й форме
СП 14.13330.2012

39.

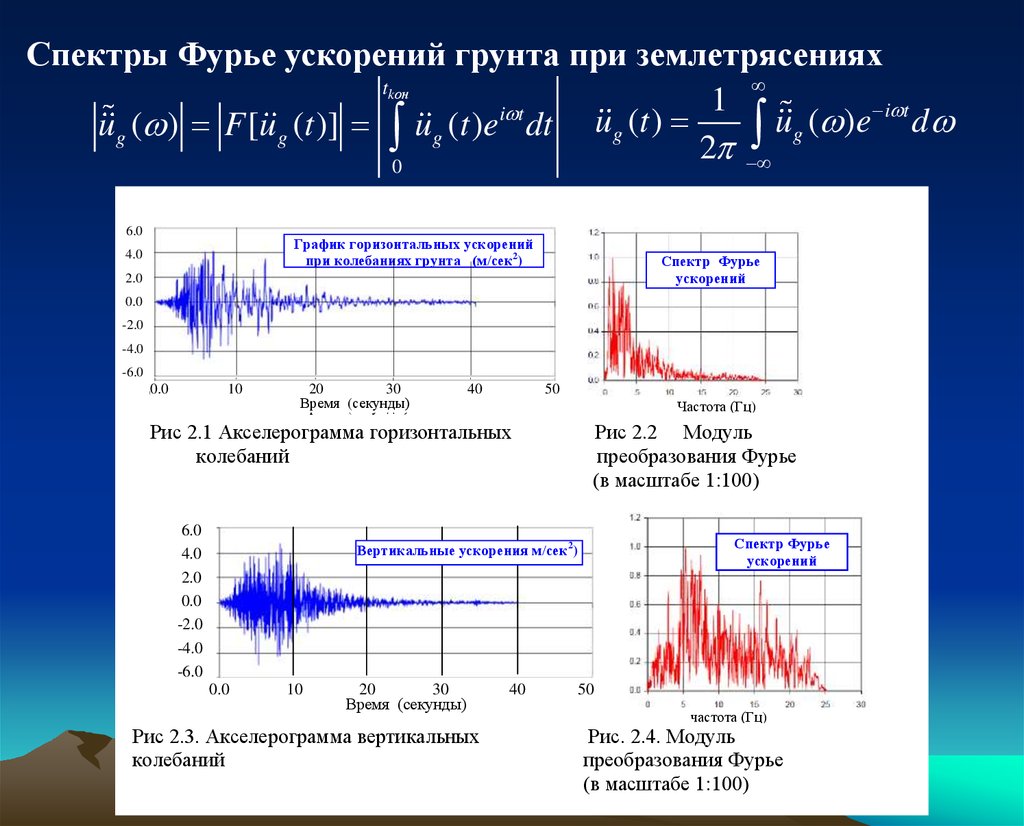
Спектры Фурье ускорений грунта при землетрясениях
tkон
1
i t
i t
u
(
t
)
u
(
)
e
d
ug ( ) F [ug (t )] ug (t )e dt
g
g
2
0
6.0
6.0
4.0
4.0
График горизонтальных
горизонтальных ускорений
ускорений
График
при
колебаниях
грунта
(м/сек22))
при колебаниях грунта (м/сек
Амплитуды
Фурье
Спектр Фурье
см/сек
ускорений
2.0
2.0
0.0
0.0
-2.0
-2.0
-4.0
-4.0
-6.0
-6.0
0.0
0.0
10
10
20
30
20
30
Время (секунды)
(секунды)
Время
40
40
50
50
Рис 2.1 Акселерограмма горизонтальных
колебаний
6.0
4.0
2.0
0.0
-2.0
-4.0
-6.0
Частота (Гц)
Рис 2.2 Модуль
преобразования Фурье
(в масштабе 1:100)
Спектр Фурье
ускорений
Вертикальные ускорения м/сек2)
0.0
10
20
30
Время (секунды)
Рис 2.3. Акселерограмма вертикальных
колебаний
40
50
частота (Гц)
Рис. 2.4. Модуль
преобразования Фурье
(в масштабе 1:100)

40.

Спектры Фурье скоростей и перемещений
u( ) ( i )u( ) ( i )2 u( )
6.0
График горизонтальных ускорений
при колебаниях грунта
4.0
Амплитуды
Фурье
Спектр Фурье
см/сек
ускорения
2.0
0.0
-2.0
-4.0
-6.0
0.0
10
0.4
0.3
0.2
0.1
0.0
-0.1
-0.2
-0.3
-0.4
20
30
время (секунды)
40
50
частота (Гц)
График скорости горизонтальных
колебаний грунта (м/сек)
0.0
10
0.15
20
30
время (секунды)
40
Спектр Фурье
скорости
50
частота (Гц)
График горизонтальных
перемещений грунта (м)
0.10
Спектр Фурье
перемещений
0.05
0.00
-0.05
-0.10
-0.15
0.0
10
20
30
время (секунды)
40
50
Функции ускорений, скоростей и перемещений
при землетрясении Loma Prieta
частота (Гц)
Спектры Фурье

41.

Соотношения между интегралом Фурье и спектрами
максимальных реакций (спектрами ответов)
представим решение дифференциального уравнения:
(4.1)
ur 2 ur 2ur ug
в виде интеграла Дюамеля:
t
1
u (t ) u g ( )sin d (t )e n (t ) d
(4.2)
d 0
Преобразуем подынтегральное выражение, используя формулу синуса
разности и положив коэффициент демпфирования равным нулю ( 0 ):
t
t
1
1
u (t ) u g ( )cos d sin t u g ( )sin d cos t
(4.3)
0
0
Продифференцировав по времени, получим:
t
t
u (t ) u g ( )cos d cos t u g ( )sin d sin t
(4.4)
0
0

42.

Соотношения между интегралом Фурье и спектрами
максимальных реакций (спектрами ответов)
Запишем преобразование Фурье функции ug (t ) :
tk
F [u g (t )] u g (t )ei t dt ,
(4.6)
0
где t k - продолжительность землетрясения.
Представим выражение (4.6) в виде суммы действительной и мнимой
части:
tk
tk
0
0
F[ug (t )] ug (t )cos tdt i u g (t )sin tdt
Амплитудный спектр Фурье F [u (t )] определяется как корень квадратный
из суммы квадратов действительной и мнимой части изображения Фурье:
2
2
tкон
tкон
(4.7)
F [u g (t )] u g (t )cos tdt u g (t )sin tdt
0
0
Если максимальное значение перемещений Sd ( ) достигается в момент
времени td tkон , то
2
td
td
S pv ( ,0) Sd ( ,0) u g ( )cos d u g ( )sin d
0
0
2
(4.8)

43.

Заключение
При задании исходной информации и при расчёте любых
сооружений
на
сейсмические
воздействия
удобно
использовать и спектры Фурье, и спектры ответов.
В нормативных документах практически во всех странах
мира используется концепция спектров ответов.
Между спектрами Фурье и спектрами ответов существует
простая связь: амплитудный спектр Фурье ускорений
колебаний грунта совпадает с псевдоспектром скоростей
Спектры Фурье представляют характеристики реальных
движений грунта, в то время как спектры ответов - это
реакции систем, находящихся на грунте, в предположении,
что колебания оснований сооружений совпадают с
колебаниями «свободного поля».
Следует отметить, что колебания основания сооружений
не совпадают с колебаниями «свободного поля».