Similar presentations:
Квантовая и ядерная физика. Раздел "Молекулярные спектры"
1. Квантовая и ядерная физика Раздел МОЛЕКУЛЯРНЫЕ СПЕКТРЫ.
Абрик Ибрагимович Валишев, к.ф. - м.н., профессор? Марлен Еновкович Топчиян , д.ф. -м.н., профессор
2. ЛЕКЦИЯ 22. МОЛЕКУЛЯРНЫЕ СПЕКТРЫ.
А.И. Валишев3. Энергия молекулы.
4. Энергия молекулы
Вклады в энергию молекулы:1. энергия электронной оболочки Ee(R)
2. энергия колебаний ядер E
3. вращательная энергия Er
Для простоты рассматривается 2-х атомная
молекула. R – расстояние между ядрами.
Замечание. Колебания ядер – (изменение взаимного
межядерного расстояния) хорошо описываются
гармоническим законом при малом изменении
взаимного расстояния. При сильном возбуждении
(внешней силе) следует учитывать следующие за
квадратичными членом разложения потенциальной
U(x) энергии по x = R – R0 , колебания становятся
ангармоничными:
M 2 x2
3
4
U ( x)
2
x x ...
5. Энергия молекулы
Частота переходаЭнергия молекулы
Ee E Er
1. Ee /ħ - определяет область спектра –
инфракрасная, ультрафиолетовая, видимая.
2. E /ħ задает полосы
3. Er /ħ Задает тонкую структуру внутри полосы
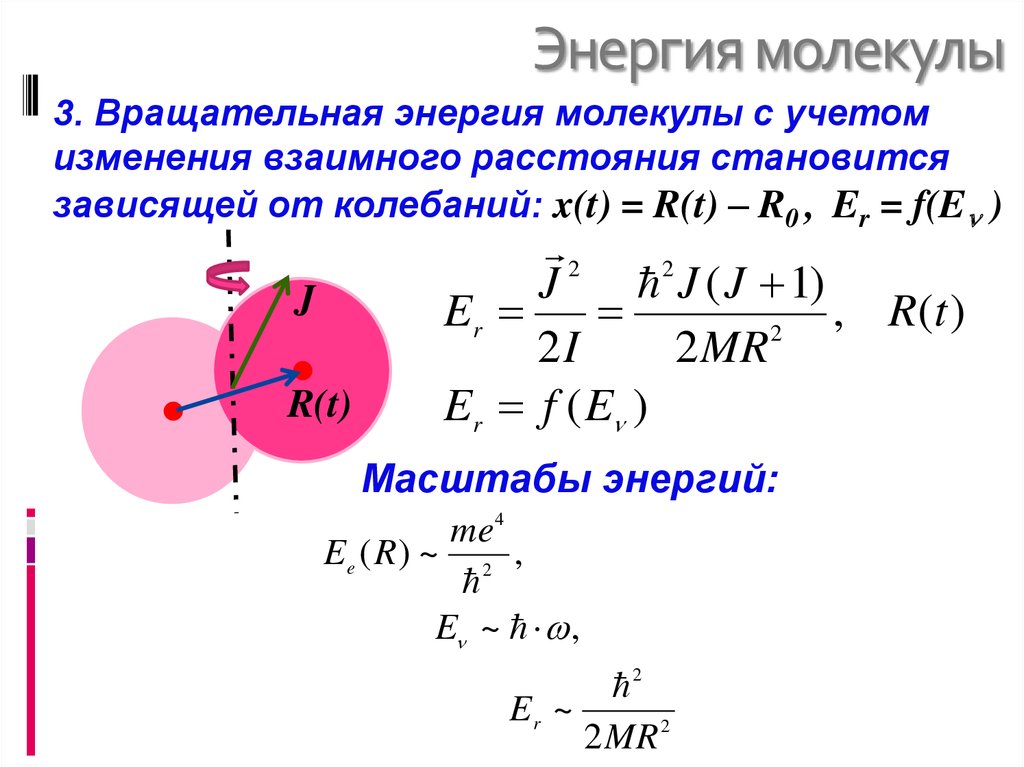
6. Энергия молекулы
3. Вращательная энергия молекулы с учетомизменения взаимного расстояния становится
зависящей от колебаний: x(t) = R(t) – R0 , Er = f(E )
J
R(t)
2
2
J
J ( J 1)
Er
, R(t )
2
2I
2 MR
Er f ( E )
Масштабы энергий:
me4
Ee ( R ) ~ 2 ,
E ~ ,
2
Er ~
2 MR 2
7. Энергия молекулы
Оценки энергий, иерархия энергий.2. Оценка энергии колебаний ядер E = ħ
~
k
, k ?
MЯ
e2
U e 2
U ( R) ~ , F
~ 2,
R
R R
2U
F k ( R R0 ) .... 2
R
( R R0 ) ...
R R0
e2
e2
2
F 3 x R R0 ,
k~ 3,
R0 ~ a1
R0
R0
me2
Изменение энергии колебаний ядер того же
порядка, что и энергия колебаний
8. Энергия молекулы
Изменение энергии колебаний ядер E тогоже порядка, что и энергия колебаний E
1/ 2
e
k
E ~
3
MЯ
M Я R0
2
1/ 2
me
6
MP
3 8
1/ 2
em
me m
2
2
MP
M
Изменение энергии колебаний ядер E
порядка энергии 1-го Боровского уровня с
множителем корня из отношения масс
электрона и протона
1/ 2
4
3/ 2
4
E
me m
2
M
4
~
9. Энергия молекулы
Изменение вращательной энергии Er попорядку величины совпадает c энергией
вращения молекулы Er
2 J ( J 1)
2
2 m 2 e 4 me4 m
~
Er
4 2
2
2
M
2 M Я R M P R0 M
Изменение энергии вращения молекулы Er
порядка энергии 1-го Боровского уровня с
множителем отношения масс электрона и
4
протона
me m
Er
~
M
2
Отношения изменений энергии:
электронной оболочки / энергии колебаний /
энергии вращения молекулы : Ee : E : Er =
10. Энергия молекулы
Изменение вращательной энергии Er попорядку величины совпадает c энергией
вращения молекулы Er
2 J ( J 1)
2
2 m 2 e 4 me4 m
~
Er
4 2
2
2
M
2 M Я R M P R0 M
Изменение энергии вращения молекулы Er
порядка энергии 1-го Боровского уровня с
множителем отношения масс электрона и
4
протона
me m
Er
~
M
2
Отношения изменений энергии:
электронной оболочки / энергии колебаний /
энергии вращения молекулы : Ee : E : Er =
11. Энергия молекулы
Отношения изменений энергии:электронной оболочки / энергии колебаний /
энергии вращения молекулы :
Ee : E : Er =
1/ 2
Ee : E : Er
m
M
m m
1: :
M M
4
5
5 10 10
Ee E
E r !!
12. Энергия молекулы
Оценка частот вращательных переходовEr = ħ r
Дипольный переход (ротационный) с
изменением квантового числа J по правилу
отбора на 1, J = 1
E r
J 1 J J J 1
r
2
2 MR0
m 2 e 4 1 me4 m
J
4 2
2
MR0
M
M
B J;
B
MR02
J
13. Энергия молекулы
Оценка частот вращательных переходовEr = ħ r
1,08 10
13
1
r
J
~ 10 сек
2
24
8 2
MR0
1,67 10 (10 )
27
2 с
6,28 3 1010
2
~
10
см
13
r
10
r ~ BJ .
Частоты вращательных переходов в далекой
инфракрасной области спектра.
Вращательные спектральные линии на равном
расстоянии интервалы малы ~ 1013 по
сравнению с другими спектральными сериями
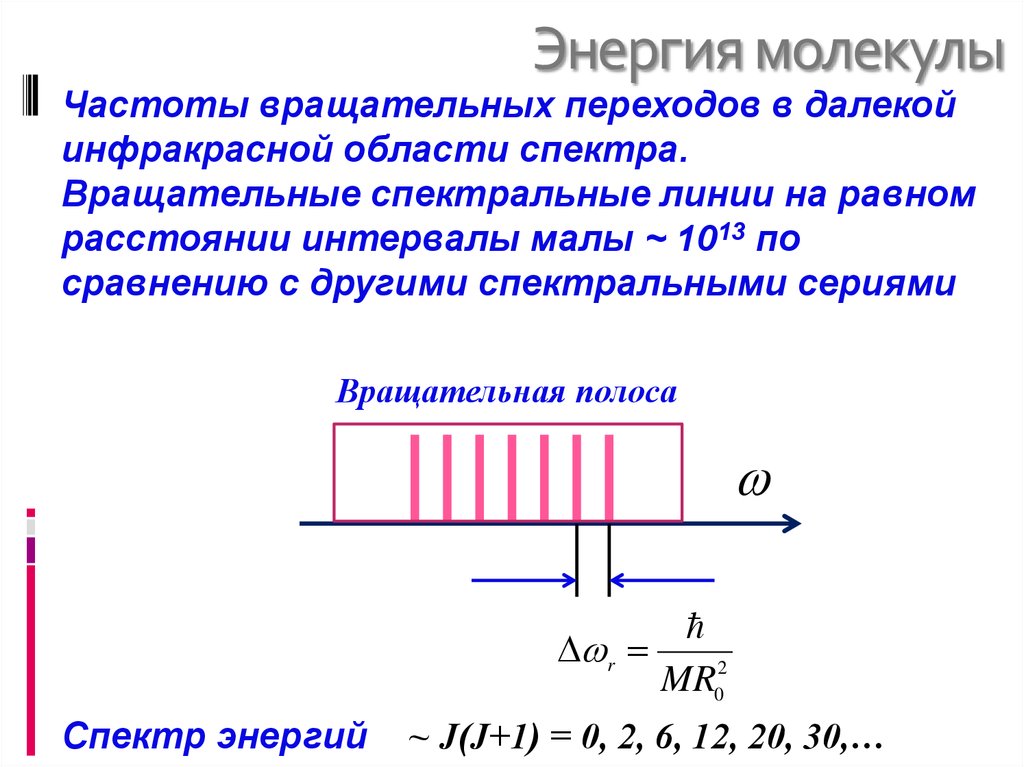
14. Энергия молекулы
Частоты вращательных переходов в далекойинфракрасной области спектра.
Вращательные спектральные линии на равном
расстоянии интервалы малы ~ 1013 по
сравнению с другими спектральными сериями
Вращательная полоса
r
MR02
Спектр энергий
~ J(J+1) = 0, 2, 6, 12, 20, 30,…
15. Энергия молекулы
Колебательно - вращательные переходы.Добавляется энергия колебаний ядер к
вращательным энергиям.
1
E n , n 1
2
E E r
r
r B J
1/ 2
M
~ r ~ 1015 сек 1 ,
~ 10 5 см
m
Полоса частот при переходах между
фиксированными колебательными уровнями и
различными вращательными лежит в ближней
инфракрасной области ~ 1015 1/сек.
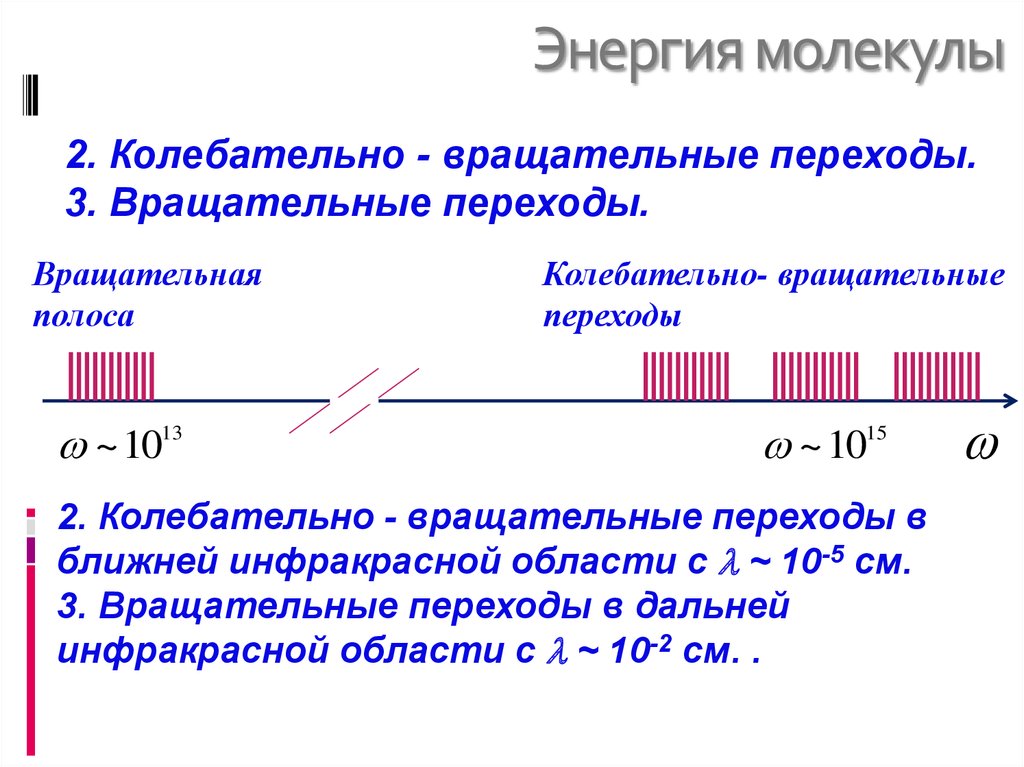
16. Энергия молекулы
2. Колебательно - вращательные переходы.3. Вращательные переходы.
Вращательная
полоса
~ 1013
Колебательно- вращательные
переходы
~ 1015
2. Колебательно - вращательные переходы в
ближней инфракрасной области с ~ 10-5 см.
3. Вращательные переходы в дальней
инфракрасной области с ~ 10-2 см. .
17. Энергия молекулы
2. Ангармонические колебательныепереходы.
А. Возникают «обертоны» малой
интенсивности с частотами 2 , 3 , 4
,…
B. Расстояния между соседними
квантовыми уровнями неодинаковы E
const. В случае идеальной, симметричной
параболы уровни энергии эквидистантны
E = const. Плотность уровней энергии
растет по мере приближения к нулевой
асимптоте – энергии свободного,
несвязанного состояния.
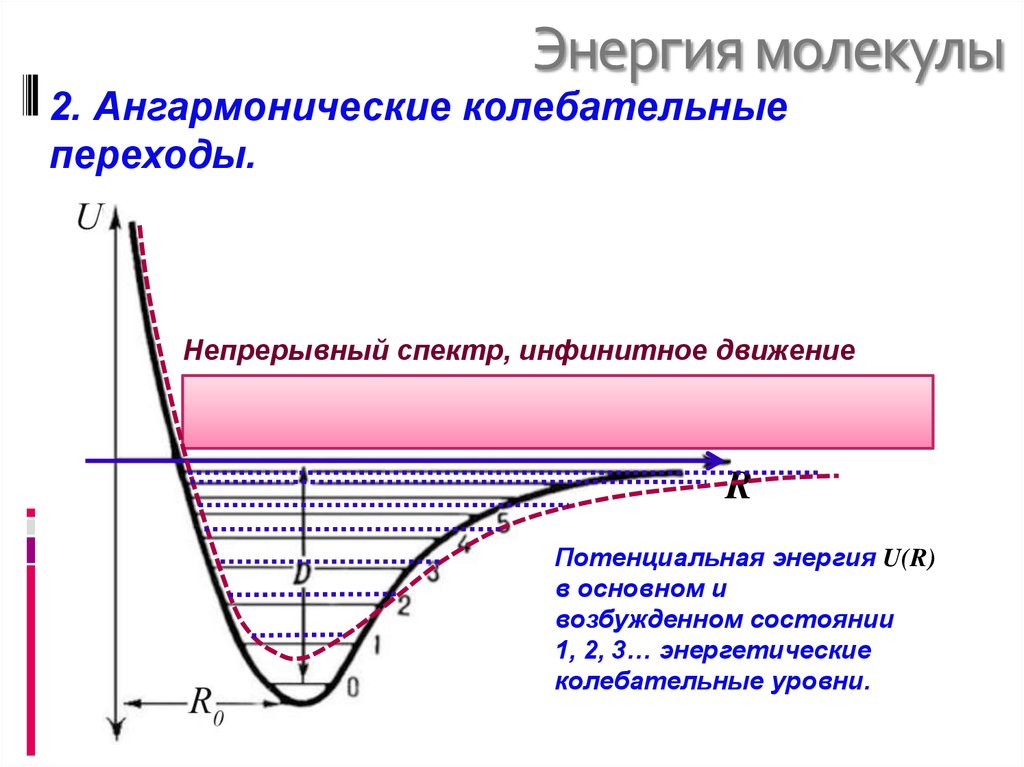
18. Энергия молекулы
2. Ангармонические колебательныепереходы.
Непрерывный спектр, инфинитное движение
R
Потенциальная энергия U(R)
молекулы в зависимости
от межатомного расстояния R
R0 – равновесное расстояние
D – энергия диссоциации
1, 2, 3… энергетические
колебательные уровни.
19. Электронно-колебательные спектры.
20. Электронно – колебательные спектры
При изменении электронной конфигурации(состояния электронной оболочки)
меняются:
1. вибрационные частоты не равны
частота перехода в возбужденном состоянии
не равна частоте перехода в основном
[невозбужденном]состоянии)
2. ротационная постоянная возбужденного
состояния отличается от ротационной
константы основного состояния B B
3. не работает правило отбора для
осциллятора n = 1
21. Энергия молекулы
2. Ангармонические колебательныепереходы.
Непрерывный спектр, инфинитное движение
R
Потенциальная энергия U(R)
в основном и
возбужденном состоянии
1, 2, 3… энергетические
колебательные уровни.
22. Электронно – колебательные спектры
Электронно – колебательные3
спектры
2
1
E e
0
0
3
2
1
0
E e
Уточненные правила
отбора для
вращательного
квантового числа
J 1
J J
J 1
1
1
E
( n ) ( n ) 0
2
2
B J ( J 1) B J ( J 1)
23. Электронно- колебательные спектры
Классификация линий по вращательномуквантовому числу при одинаковости
электронных и колебательных переходов.
Электронно – колебательная полоса
состоит из 3-х ветвей
1. R J J 1
2. Q J J
3. P J J 1
24. Электронно- колебательные спектры
1. R J J 12. Q J J
3. P J J 1
1.
J J 1, 0 B J ( J 1) B ( J 1) J
B B J B B J
2
0
0 ( B B ) J ( J 1)
2.
J J ,
3.
J J 1, 0 2 B B 3B J B B J 2
25. Электронно- колебательные спектры
Основной вклад в частоту перехода отизменения энергии электронной оболочки
Ee
,
Ee M
~
m
Ee
E
1/ 2
E
Электронно – колебательные полосы лежат
в оптической и ближней ультрафиолетовой
области спектра.
Для всех линий частота пропорциональна
квадрату вращательного квантового числа J.
Плотность спектральных линий нарастает
при малых J
26. Электронно- колебательные спектры
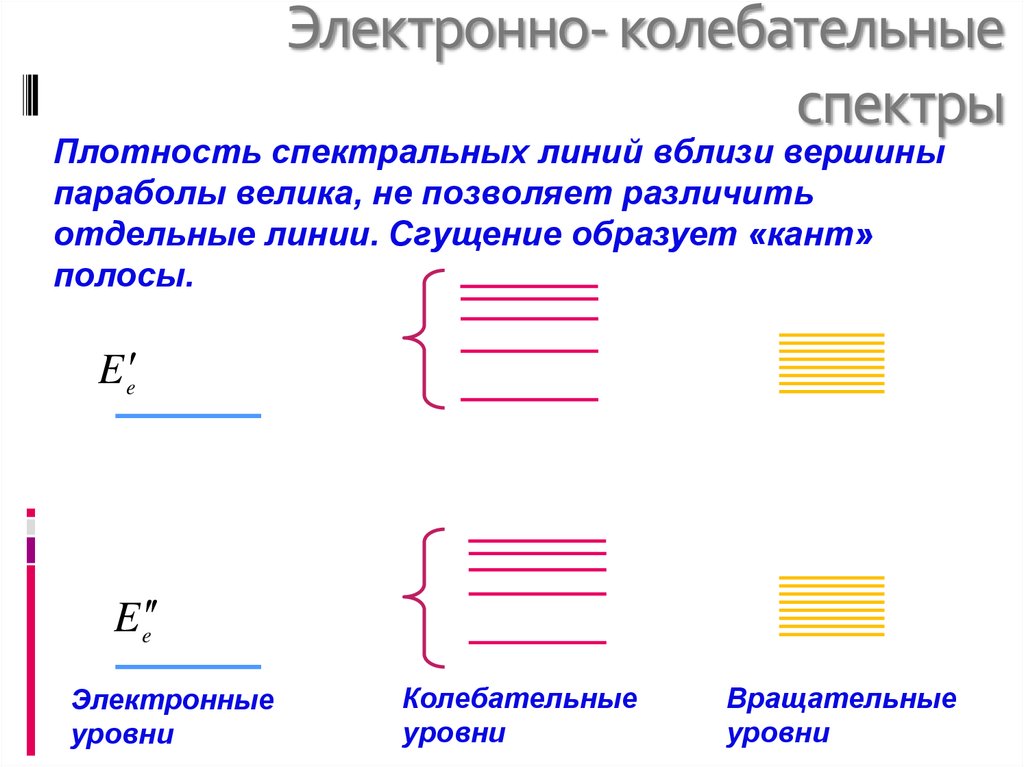
Плотность спектральных линий вблизи вершиныпараболы велика, не позволяет различить
отдельные линии. Сгущение образует «кант»
полосы.
E e
E e
Электронные
уровни
Колебательные
уровни
Вращательные
уровни
27. Электронно- колебательные спектры
28. Комбинационное рассеяние.
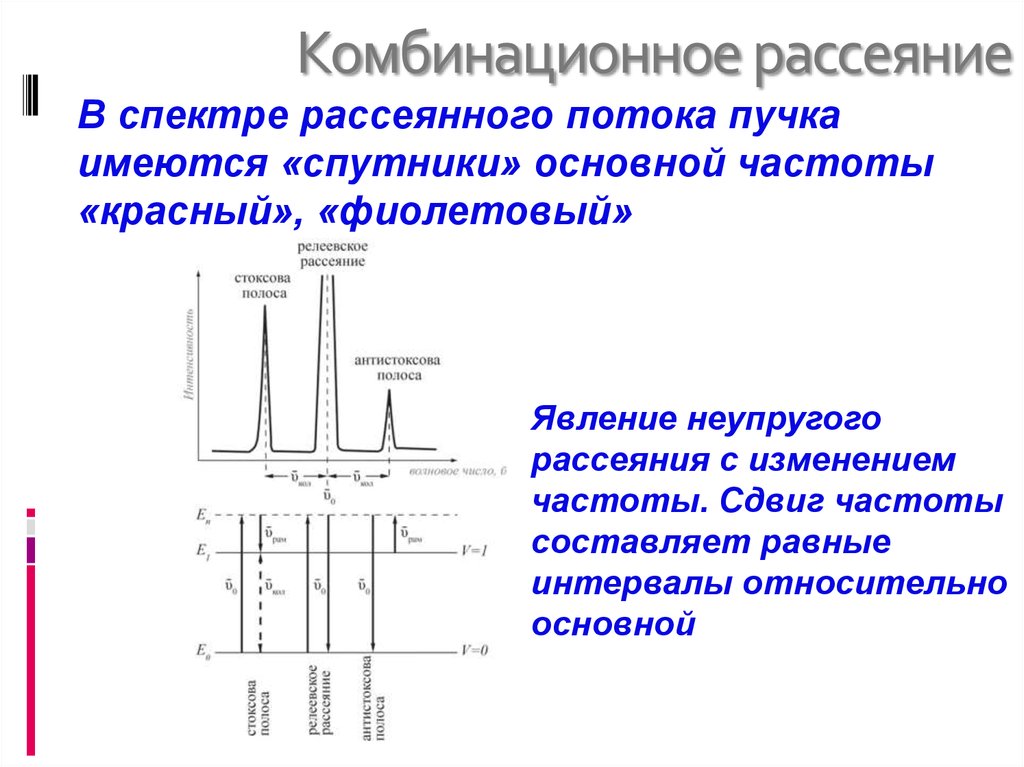
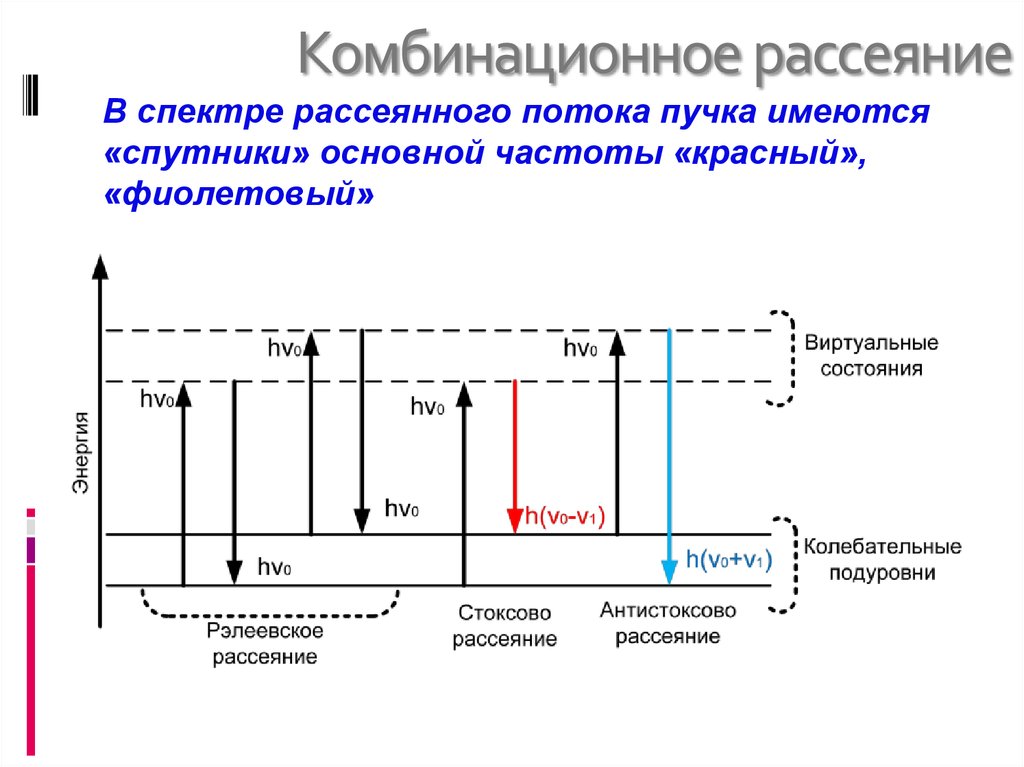
29. Комбинационное рассеяние
В спектре рассеянного потока пучкаимеются «спутники» основной частоты
«красный», «фиолетовый»
Явление неупругого
рассеяния с изменением
частоты. Сдвиг частоты
составляет равные
интервалы относительно
основной
30. Комбинационное рассеяние
В спектре рассеянного потока пучка имеются«спутники» основной частоты «красный»,
«фиолетовый»
31. Комбинационное рассеяние
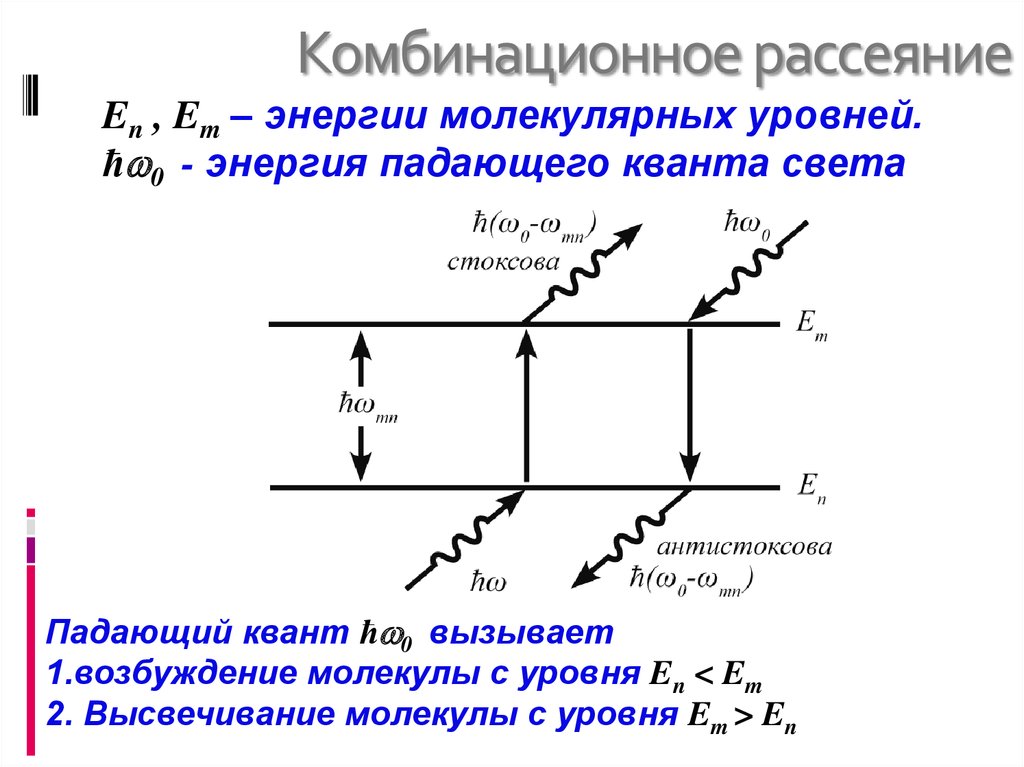
En , Em – энергии молекулярных уровней.ħ 0 - энергия падающего кванта света
Падающий квант ħ 0 вызывает
1.возбуждение молекулы с уровня En < Em
2. Высвечивание молекулы с уровня Em > En
32. Комбинационное рассеяние
En , Em – энергии молекулярных уровней.ħ 0 - энергия падающего кванта света
1 0 ( Em En ),
1 0 ( Em En ),
0 - в оптическом диапазоне.
1 0 mn
2 0 mn
Интенсивности линий комбинационного рассеяния
существенно меньше интенсивности основной.
«Фиолетовый» спутник имеет интенсивность
пропорциональную:
I ~e
Em En
kT
33. Интернет ресурс
http//:edu.ci.nsu.ruКурс лекций
Задачник


























 physics
physics








