Similar presentations:
Колебательная энергия и колебательные спектры двухатомных молекул. Лекция 12
1. Лекция 12
Колебательная энергия и колебательныеспектры
двухатомных
молекул.
Приближение
гармонического
и
ангармонического
осцилляторов.
Колебательно-вращательные состояния
и спектры двухатомных молекул
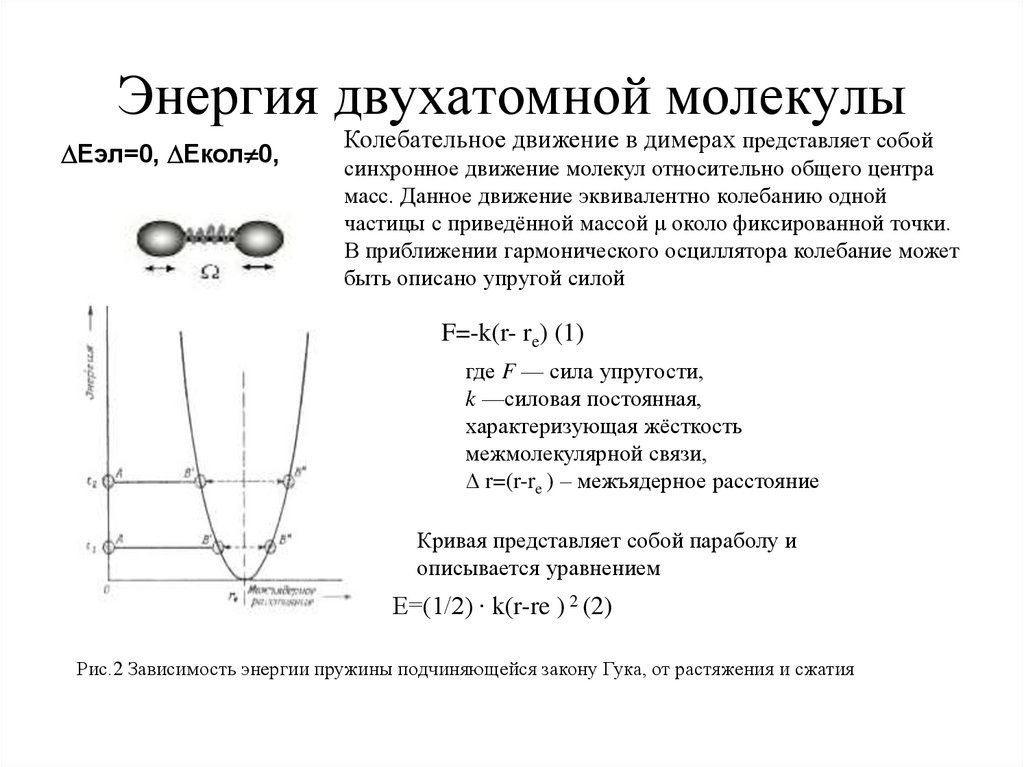
2. Энергия двухатомной молекулы
Еэл=0, Екол 0,Колебательное движение в димерах представляет собой
синхронное движение молекул относительно общего центра
масс. Данное движение эквивалентно колебанию одной
частицы с приведённой массой μ около фиксированной точки.
В приближении гармонического осциллятора колебание может
быть описано упругой силой
F=-k(r- re) (1)
где F — сила упругости,
k —силовая постоянная,
характеризующая жёсткость
межмолекулярной связи,
∆ r=(r-re ) – межъядерное расстояние
Кривая представляет собой параболу и
описывается уравнением
Е=(1/2) ∙ k(r-re ) 2 (2)
Рис.2 Зависимость энергии пружины подчиняющейся закону Гука, от растяжения и сжатия
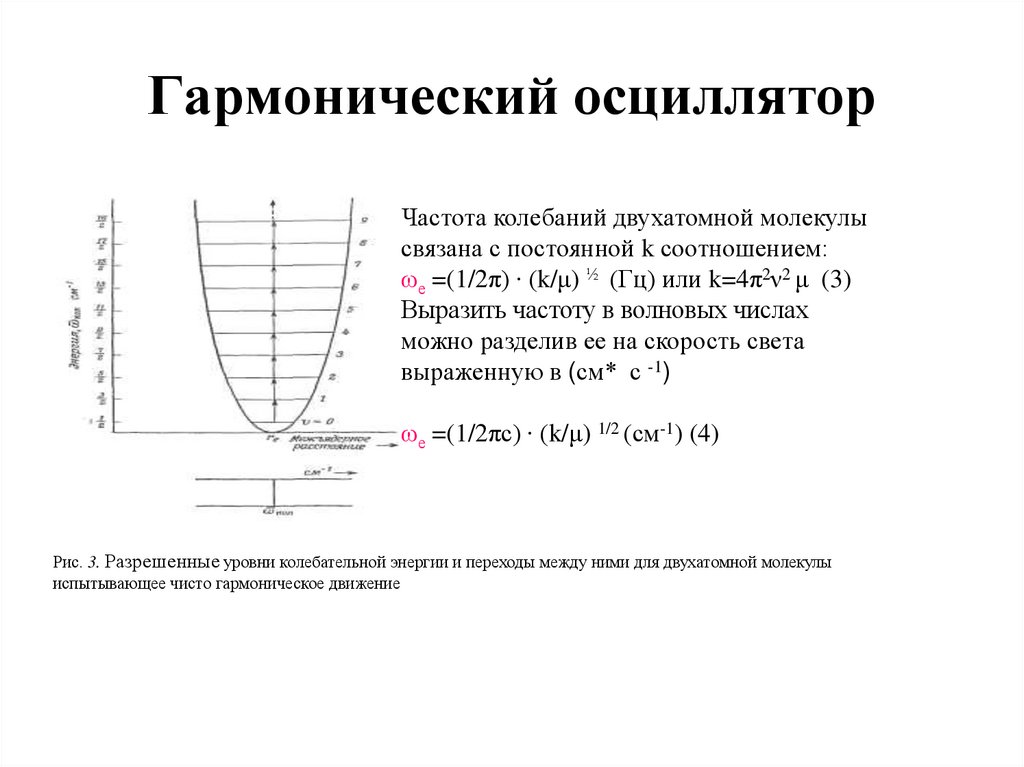
3. Гармонический осциллятор
Частота колебаний двухатомной молекулысвязана с постоянной k соотношением:
ωе =(1/2π) ∙ (k/μ) ½ (Гц) или k=4π2ν2 μ (3)
Выразить частоту в волновых числах
можно разделив ее на скорость света
выраженную в (см* с -1)
ωе =(1/2πc) ∙ (k/μ) 1/2 (см-1) (4)
Рис. 3. Разрешенные уровни колебательной энергии и переходы между ними для двухатомной молекулы
испытывающее чисто гармоническое движение
4.
Решение уравнения Шредингера для гармонического осциллятора имеет вид:
Е кол =(v+1/2) ∙ (h/2π) ∙ (k/μ) 1/2 (5)
В квантовой теории, которая описывает образование спектра,
колебательная энергия Екол квантуется, т.е. должна принимать только
определенные значения:
Екол =( +1/2)hωе (6)
где =0,1,2,..., - колебательное квантовое число, а ωе = (1/ 2π)(k/μ) 1/2
- собственная частота: т.е. Екол представлена системой равноотстоящих
энергетических уровней. Из выражения (6) следует, что энергия
гармонического осциллятора может принимать только дискретные значения,
равные 0,5 h ωе ; 1,5 h ωе ; 2,5 h ωе и т.д..
В соответствие с правилами отбора: = 1, спектр гармонического
осциллятора представляет одну линию с частотой ωе .
Наименьшее значение колебательной энергии, соответствующее v=0,
называется нулевой энергией (Е 0 ):Если =0, то
Е0 =1/2hωе, (7)
Величина 1/2hωе называется нулевой энергией; она зависит только от
классической колебательной частоты и, следовательно, только от силы
химической связи и масс атомов. Наличие нулевой энергии является
отражением основного различия между квантовомеханическим и
классическим описаниями молекулярных колебании. Согласно классической
механике, молекула вполне может перестать колебаться вообще, в то время
как квантовая механика настаивает на том, что какие-то колебания всегда
должны иметь место. Существование нулевых колебаний убедительно
подтверждено экспериментами.
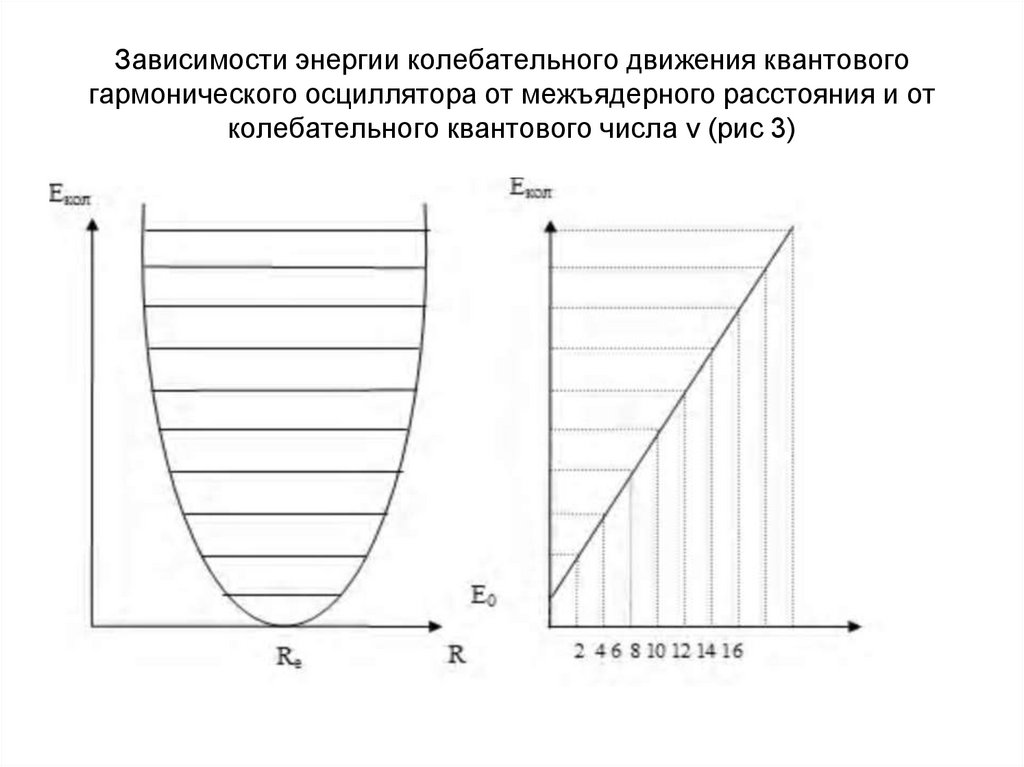
5. Зависимости энергии колебательного движения квантового гармонического осциллятора от межъядерного расстояния и от
колебательного квантового числа v (рис 3)6.
• Разность двух соседних энергетических состояний у гармоническогоосциллятора постоянна и равна
• ∆ E кол =E кол (v+1)-E кол (v)=h ωе . (8)
• Частота поглощения или излучения, соответствующая переходу с
одного колебательного уровня на другой:
• ν кол = ∆ E кол /h. (9)
• Сравнение энергии колебательного движения со средней энергией
поступательного движения молекул показывает, что при тепловом
равновесии вещества подавляющее число молекул находится на
нулевом колебательном уровне (v=0) или, как говорят, в основном
состоянии. Отсюда следует, что с заметной вероятностью
осуществляются только переходы (с v=0 на v=1), при которых
колебательное число изменяется на ±1. Поэтому ν кол = ωе.
• Следовательно, для гармонического осциллятора характерно
следующее свойство: гармонический осциллятор поглощает или
излучают кванты энергии такой же частоты, с которой он сам
колеблется.
7. Ангармонический осциллятор
• Колебания димеров близки к гармоническим при малыхамплитудах (рис.4). Если же димер заметно отклоняется
от положения равновесия, то колебания перестают быть
гармоническими в силу различной зависимости сил
отталкивания и притяжения от межмолекулярного
расстояния. По этой причине амплитуда колебания
димера, соответствующая сближению молекул в димерах,
меньше амплитуды, соответствующей удалению их друг
от друга. В этом случае закон Гука F=k(r-r e ) не
выполняется и зависимость Eкол перестает быть параболой
(рис.4).
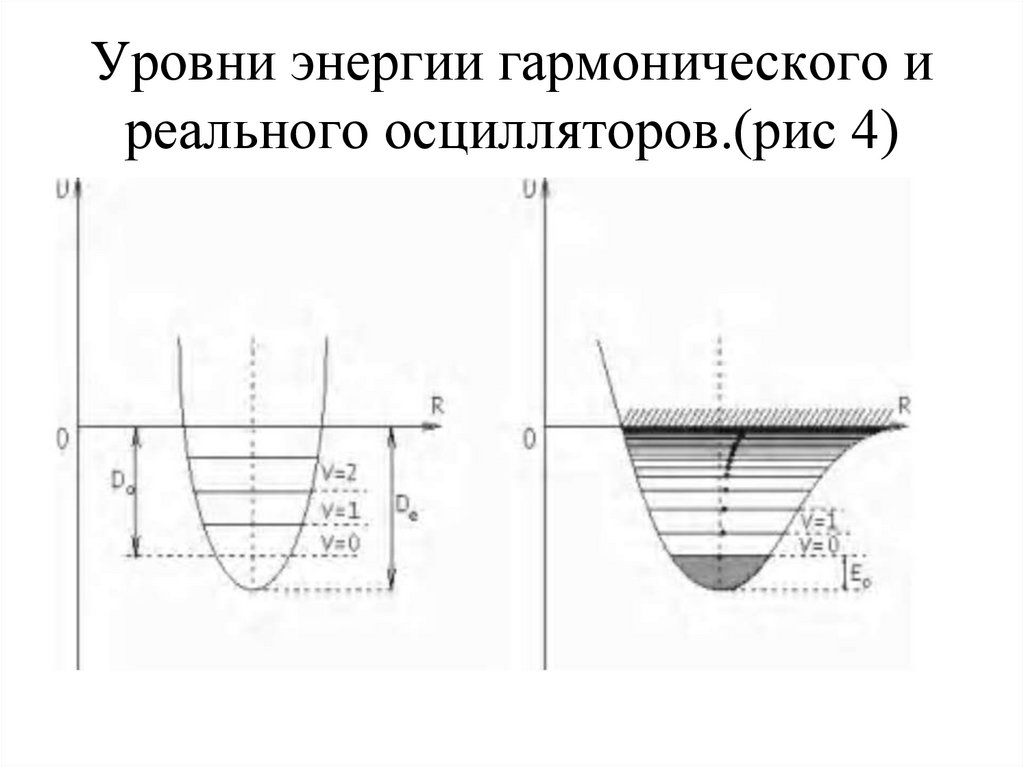
8. Уровни энергии гармонического и реального осцилляторов.(рис 4)
9. Ангармонический осциллятор
Зависимость Eкол удачно описывается эмпирическойфункцией Морзе
Е=Dе [1-eхр (a(r-re))]2
(10)
De
Рис. 5. Кривая Морзе: энергия
двухатомной молекулы, испытывающей
ангармонические растяжения и сжатия
где а — постоянная, характерная для данной
молекулы,
De- энергия диссоциации
De=hcωe/4xe
a=(8π2cµωexe/h)1/2
ωexe-коэффициент ангармоничности колебания См-1,
м-1
xe-коэффициент
ангармоничности
колебания
(величина безразмерная),значение которой для
валентных колебаний всегда мало и положительно
(≈+0,01); следовательно, с ростом колебательные
уровни все более тесно сближаются друг с другом.
Первые несколько уровней изображены на рис. 6.
10.
Решение уравнения Шредингера после подстановки в неговыражения (10), дает решение:
Е кол (v) =(v+1/2)hсω е -(v+1/2) 2 hсω е х е . (11)
xе=hωe/4De
( 12)
Максимальное значение колебательного квантового числа
vmax=(1-xe)/2xe
( 13)
Максимальная энергия колебательного движения
-энергия диссоциации De отсчитываемая от минимума
потенциальной кривой
Рис. 6 Разрешенные уровни колебательной
энергии и некоторые переходы между
ними для двухатомной молекулы,
совершающейангармонические колебания.
( 14)
Еv, max=hcωe/4xe=De
Для перевода молекулы с нулевого на
максимальный колебательный квантовый
уровень v max необходима энергия :
D0= Еv, max- Еv,0= hcωe/4xe (1-xe)2 (15)
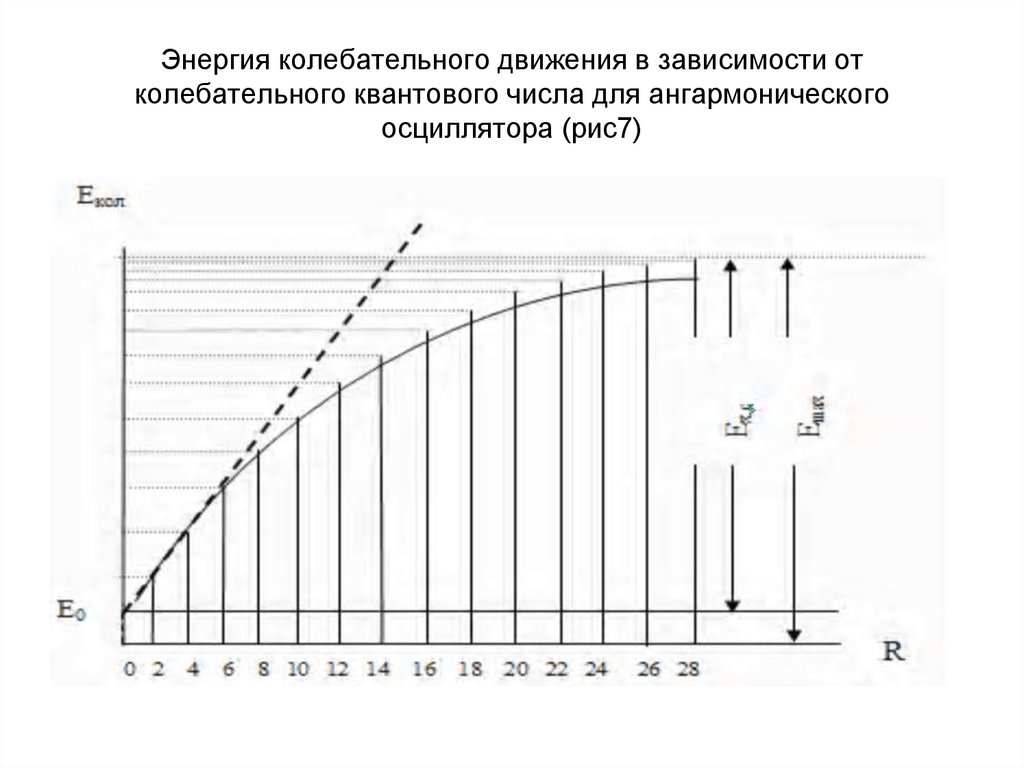
11. Энергия колебательного движения в зависимости от колебательного квантового числа для ангармонического осциллятора (рис7)
12. Ангармонический осциллятор
• Колебательная энергия гармоническогоосциллятора может принимать
неограниченно большое значение, так как
никаких ограничений, кроме дискретности, на
величину v не накладывается.
Колебательная энергия ангармонического
осциллятора при определенном значении
колебательного числа (v=v max ) достигает
значения максимального значения Е max ,
соответствующего энергии диссоциации
димера.
13. Ангармонический осциллятор
Ангармонический осциллятор
Энергия химической связи:
Ехим.св.= (Еv, max- Еv)Na
(16)
Определим изменение энергии колебательного движения, соответствующие
переходам с v=0 на v=1, 2, 3 (рис.6) и приравняем это изменение ( ∆ Е) к энергии
кванта поглощенного излучения (hωс):
∆ Е=hωс=(v+1/2)hω ес -(v+1/2) 2 hω есх е –(1/2)hω ес+(1/4)hω есх е , (17)
где v – колебательное квантовое число уровня, на который происходит переход
молекулы с нулевого уровня при поглощении кванта энергии. Из (17) следует:
ω=vω е [1-(v+1)х е ]. (18)
Для значений v=1, 2, 3, получаем систему уравнений:
ω=ωе(1-2 х е ),
(19)
ω 1 =2ω е (1-3 х е ),
ω 2 =3ω е (1-4 х е ), где ω - основная частота (волновое число) полосы
поглощения, соответствующая переходу с нулевого квантового уровня (v=0) на
первый колебательный уровень (v=1). Основной эта частота называется потому,
что вероятность перехода с уровня v=0 на уровень с v=1 максимальна.
Вероятности перехода с v=0 на v=2 (первый обертон) и с v=0 на v=3 (второй
обертон) значительно меньше, поэтому интенсивности спектральных линий,
соответствующие этим переходам, намного меньше интенсивности основной
частоты.
Правило отбора для ангармонического осциллятора
14. Условное изображение линий в спектре ангармонического осциллятора Рис.8.
На рис.8 схематически изображен колебательный спектр димера как рядсходящихся дискретных линий, переходящий в непрерывный спектр. Таким
образом, пока энергия возбуждения димера меньше Emax, димер может
воспринимать лишь определенные кванты энергии, т.е. он способен
поглощать излучение только такой частоты, которая соответствует одной из
линий спектра (рис.4). При энергии возбуждения больше Emax димер
диссоциирует на отдельные молекулы, а последние, находясь в свободном
состоянии, могут воспринимать любое количество энергии.









 physics
physics








