Колебательно– вращательные спектры двухатомных молекул. Классическая теория

1. Лекция 8. Колебательно– вращательные спектры двухатомных молекул. Классическая теория

Колебания
1
U ke q 2
2
2
p
1
Для колебаний двухатомной молекулы полная энергия: H E
ke q 2
2 2
H
H
q
,
Уравнения движения в форме Гамильтона: p
p
q
Потенциальная энергия U как функция приращения q:
После дифференцирования: q
ke
q 0, общее решение: q q0 cos( 2 t )
2 2
Подстановка дает: q 0 4 cos( 2 t )
откуда
1 ke
2
ke
q0 cos( 2 t ) 0,

2. Вращение

Функция Гамильтона и вращательная энергия:
2E
,
Ie
Угловая скорость и момент:
Угол Эйлера изменяется с частотой:
P2 1
H E
I e 2
2I e 2
P 2I e E
t 0 2 r t 0
Дипольный момент
Разложение в ряд:
1 2 2
z e ( ) e q ( 2 ) e q ...
q
2 q
1 2 2
1 2 2
e ( 2 ) e q0 ( ) e q0 cos(2 t ) ( 2 ) e q0 cos(2 2 t 2 )...
4 q
q
4 q
Если учесть классическое вращение,
1 2 2
1
x [ e ( 2 ) e q0 ] cos(2 r t 0 ) ( ) e q0 {cos[2 ( r )t 0 ]
4 q
2 q
cos[2 ( r )t 0 ]} ...

3. Испускание и поглощение

В спектрах испускания и поглощения могут проявляться частоты
r , r , r , ...
если выполняются условия:
1 2 2
e ( 2 ) e q0 0,
4 q
( )e 0
q
Комбинационное рассеяние
По аналогии
где
0
x представится в виде ряда Фурье, содержащего члены с частотам
0 , 0 2 r , 0 ( 2 r ), ...
– частота релеевского рассеяния,
0 2 r
– частота, соответствующая вращательному КР,
0 ( 2 r ) – частота, соответствующая колебательно–вращательному КР.

4. Квантовая механика

p2
Оператор кинетической энергии: Tv
2
Потенциальная энергия колебаний – E
el
h2 d 2
,
Tv 2
2
8 dq
Ee U (q ) .
Гармоническое приближение
1
h ke
1
1
U k e q 2 , откуда E
(v ) = h (v )
2
2
2
2
1. Наинизшее значение энергии
h ke 1 1
h
2 2 2
2. Колебательные уровни эквидистантны: E E v 1 E v h
В этом случае
r v re
1
1
3h
1
Среднее значения обратного квадрата: 2 2
(
v
) ...
4
2
r
re 2 re k e
E

5.

Ангармоническое приближение
U (q ) De (1 e q ) 2
Потенциал Морзе:
где q r re , De E ( ) E ( re ) ,
el
el
ke
2 De
После подстановки в уравнение Шредингера:
или
где
h 2 De
1 h 2 2
1
Ev
( v ) 2 (v ) 2
2
2 8
2
1
1
Ev hc[ e (v ) e xe (v ) 2 ]
2
2
2 De
1 k e класс
h 2
e
,
e xe 2
2 c
2 c
с
8
1
1 2
В виде терма:
Gv e (v ) e xe (v ) при этом e xe e .
2
2
Разность соседних термов: G 1 G (v 1) G (v ) e 2 e xe (v 1)
v
2
e2
Энергия диссоциации:
De hc
,
D0 De E0
4 e xe
1
1 2
1 3
В общем случае: E v hc[ e (v ) e xe (v ) e y e (v ) ...
2
2
2

6. Колебательно- вращательные состояния

В приближении ”жесткий ротатор – гармонический осциллятор”:
Ev , J
1
G(v) F ( J ) hc[ e (v ) BJ ( J 1)]
2
В приближении ”нежесткий ротатор – ангармонический осциллятор”:
Ev , J
1
1 2
G(v) F ( J ) hc[ e (v ) e xe (v ) Bv J ( J 1) Dv J 2 ( J 1) 2 ]
2
2
Возможны переходы, для которых
R2 0

7.

Колебательно- вращательные переходы
Правила отбора: e 0, (
) e 0 , откуда
q
Волновые числа линий:
E 'v, J E ' 'v , J
hc
v v' v' ' 1, 2, 3...
J J ' J ' ' 1
G (v' ) G (v' ' ) Bv ' J ' ( J ' 1) Bv '' J ' ' ( J ' ' 1)
Для фиксированных колебательных уровней: v 'v '' Bv ' J ' ( J ' 1) Bv '' J ' ' ( J ' ' 1)
R ветвь , J ' J ' ' 1 , ( J ' ' J ) :
R ( J ) v 'v '' Bv ' ( J 1)( J 2) Bv '' J ( J 1)
v 'v '' 2 Bv ' (3Bv ' Bv '' ) J ( Bv ' Bv '' ) J 2
J 0,1,2,3...
P ветвь , J ' J ' ' 1 , ( J ' ' J ) :
P ( J ) v 'v '' Bv ' ( J 1) J Bv '' J ( J 1)
v 'v '' ( Bv ' Bv '' ) J ( Bv ' Bv '' ) J 2
J 1,2,3...

8.

Определение молекулярных постоянных из спектра
v01 = G (1) G (0) e 2 e xe ,
v02 = G (2) G (0) 2 e 6 e xe ,
Для колебательного перехода 0-1
для 0-2
e , e xe
откуда
Комбинационные соотношения:
v ( J 1) P ( J 1)
v (J ) P (J )
Bv ' R
или Bv '' R
1
1
4( J )
4( J )
2
2
Равновесное значение:
1
Bv Be (v )
2
Для HCl
10 2885,85 см , e 2989,1 см , e x e 51,69 см ,
-1
-1
-1
-1
-1
B0 10,42 см , B1 10,12 см .

9. Колебательно-вращательные спектры комбинационного рассеяния

Вращательные спектры:
Правило отбора
E'r E' 'r
0
hc
J ' J ' ' 2,
( J ) 0 [6B0 4B0 ]
Колебательно–вращательные спектры:
0 [G(v' ) G(v' ' ) Fv ' ( J ' ) Fv" ( J " )]
Приближенно:
0 [G(v' ) G(v' ' )]
Наиболее интенсивны в спектры КР переходы 0-1 (стоксовый) и 1-0
(антистоксовый) , например:
0 [G(1) G(0)] 0 G1 / 2
Все двухатомные молекулы дают чисто вращательные или колебательно–
вращательные спектры КР

10.

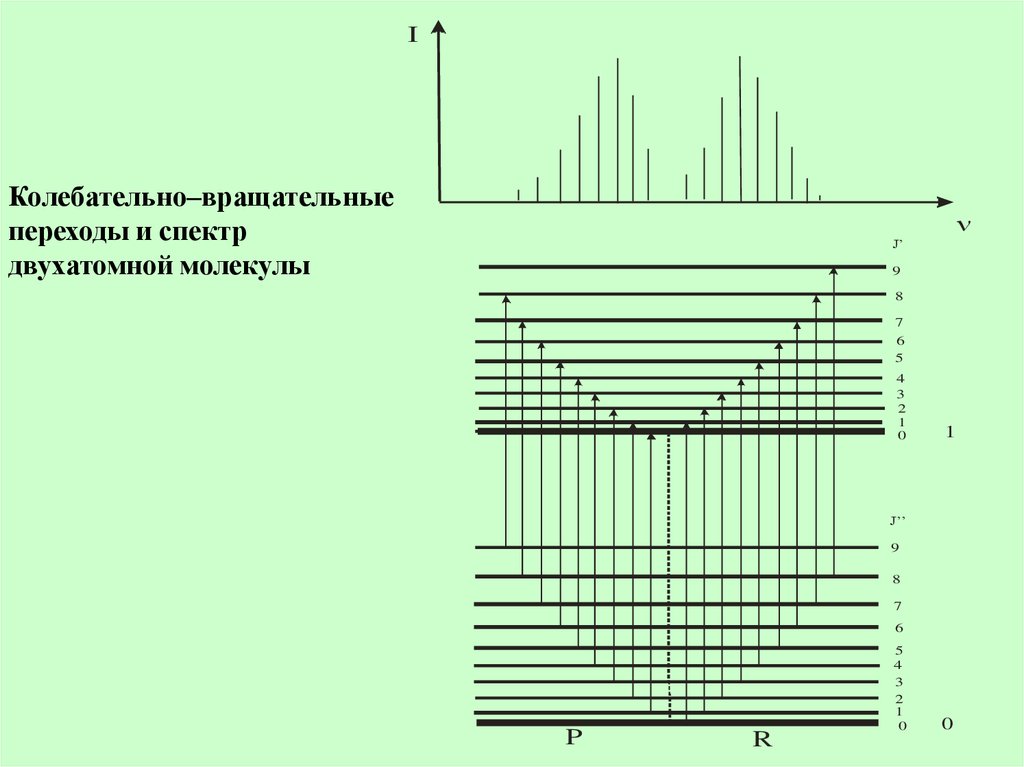
I
Колебательно–вращательные
переходы и спектр
двухатомной молекулы
J’
9
8
7
6
5
4
3
2
1
0
1
J’’
9
8
7
6
P
R
5
4
3
2
1
0
0

11.

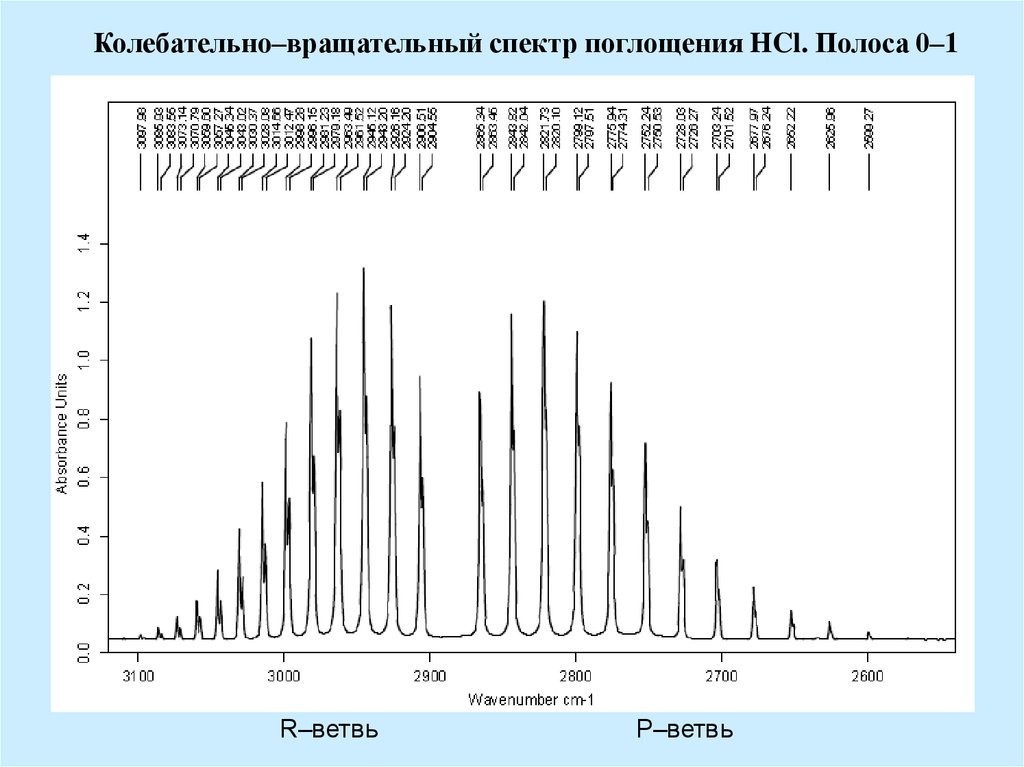
Колебательно–вращательный спектр поглощения HCl. Полоса 0–1
R–ветвь
Р–ветвь