Классификация электронных состояний двухатомных молекул

1. Классификация электронных состояний двухатомных молекул

Квадрат суммарного вектора L момента количества движения всех электронов
молекулы:
2
h
L2 = 2 L(L 1)
4
где L – соответствующее квантовое число.
Проекции орбитального момента количества движения на линию, соединяющую ядра
молекулы:
M x y M L
h
2
M L - квантовое число проекции орбитального момента:
M L L, ( L 1),... 1, 0, 1... ( L 1), L . но свойства определяются M L .
0, 1, 2, 3...
соответствуют символам
, , , ...

2. Спин, компонеты мультиплета

2
h
Квадрат вектора суммарного спина всех электронов S 2 : S2 =
S ( S 1)
2
4
h
Проекция суммарного вектора на межъядерную ось:
S x y
2
где - квантовое число проекции суммарного спина:
S , ( S 1),... 1,0, 1... ( S 1), S
Совокупность 2S 1 состояний – мультиплет. Энергия компонента
мультиплета:
E E 0 A
1
2
1
2
1
2
Например, для состояния 2 ( 1, S , , ):
E
1
2
E0
1
A
2
E
1
2
E0
1
A.
2
Квантовое число суммарной проекцией орбитального и спинового моментов:
1 3
2 2
И компоненты дублета будут обозначаться как 2 3 / 2 и 2 1 / 2 .
, в примере
1
1
1 1
2 2

3.

Свойства симметрии электронных волновых функций
Невырожденные: или .
Вырожденные: ( , , ... , для которых 0 ) – и
Если есть центр инверсии, то g , g или u , u .
Последовательность электронных состояний – X , A, B, C...
Электронно-колебательно вращательные спектры
Если
E ' hcTe' + hcG ' (v' ) + hcFv'' ( J ' ) ,
E ' ' hcTe'' + hcG ' ' (v' ' ) + hcFv'''' ( J ' ' ) ,
Te' Te'' G ' (v' ) G ' ' (v' ' ) Fv'' ( J ' ) Fv'''' ( J ' ' ) .
Без учета вращения для фиксированных электронных состояний
e','' G ' (v' ) G ' ' (v' ' ) ,
тогда совокупность наблюдаемых переходов:
то:
1
2
1
2
v ',v '' = e','' G ' (v' ) G ' ' (v' ' ) = e','' + [ e' (v' ) ' e x' e (v' ) 2 ] 1
1
[ e'' (v' ' ) ' ' e x' ' e (v' ' ) 2 ] .
2
2

4.

Таблица Деландра
v''
0
1
2
3
0
00
01
02
03
1
10
...
...
...
2
20
...
...
...
3
30
...
...
...
v'

5.

Серии переходов в
электронно–колебательных
спектрах
Система уравнений для поперечной серии:
v ',0'' = e','' G ' (v' ) G ' ' (0)
v',1'' = e','' G ' (v' ) G ' ' (1)
…………………………….
Вычитая, получаем:
v ',0'' - v',1'' = G ' ' (1) G ' ' (0) = G1''/ 2 = e'' 2 e'' xe''
v',1'' - v ', 2'' = G ' ' (2) G ' ' (1) = G3'' / 2 = e'' 4 e'' xe''
………………………………………………………
Продольная и поперечная
серии

6.

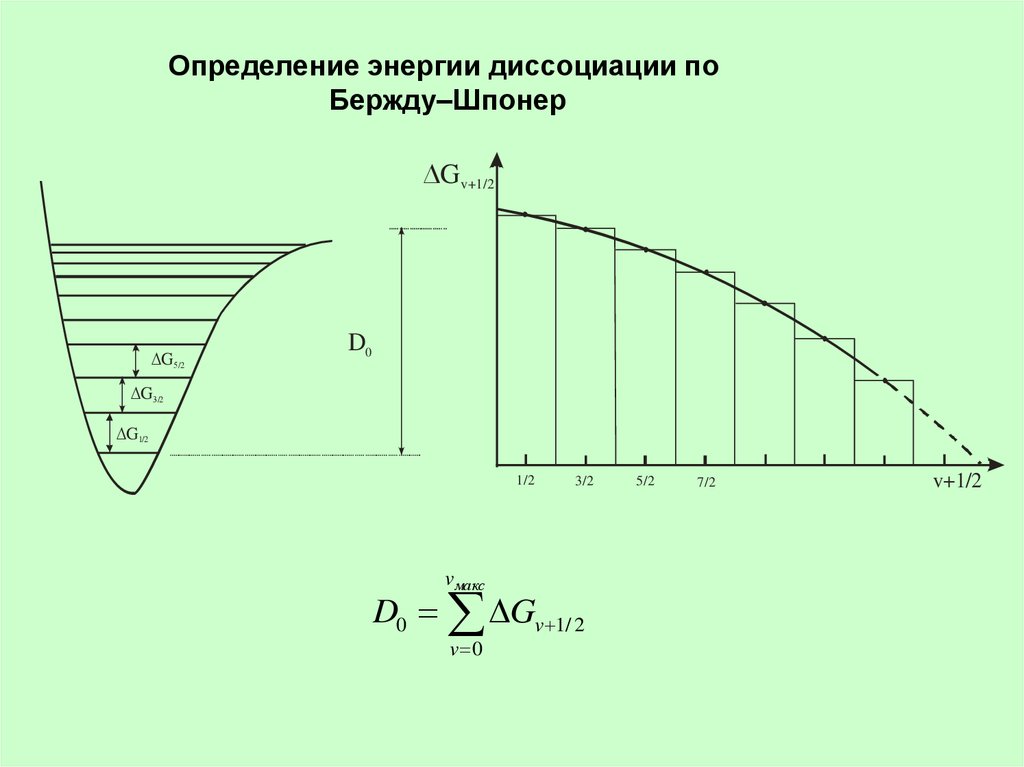
1/2
Определениепо
энергии диссоциации
Определение энергии диссоциации
по экспериментальным данным
Бержду–Шпонер
3/2
5/2
7/2
v+1/2
Gv+1/2
G5/2
D0
G3/2
G1/2
1/2
3/2
5/2
7/2
v+1/2
v макс
D0 Gv 1/ 2
v 0
G5/2
D0

7. Интенсивности колебательных переходов. Принцип Франка-Кондона

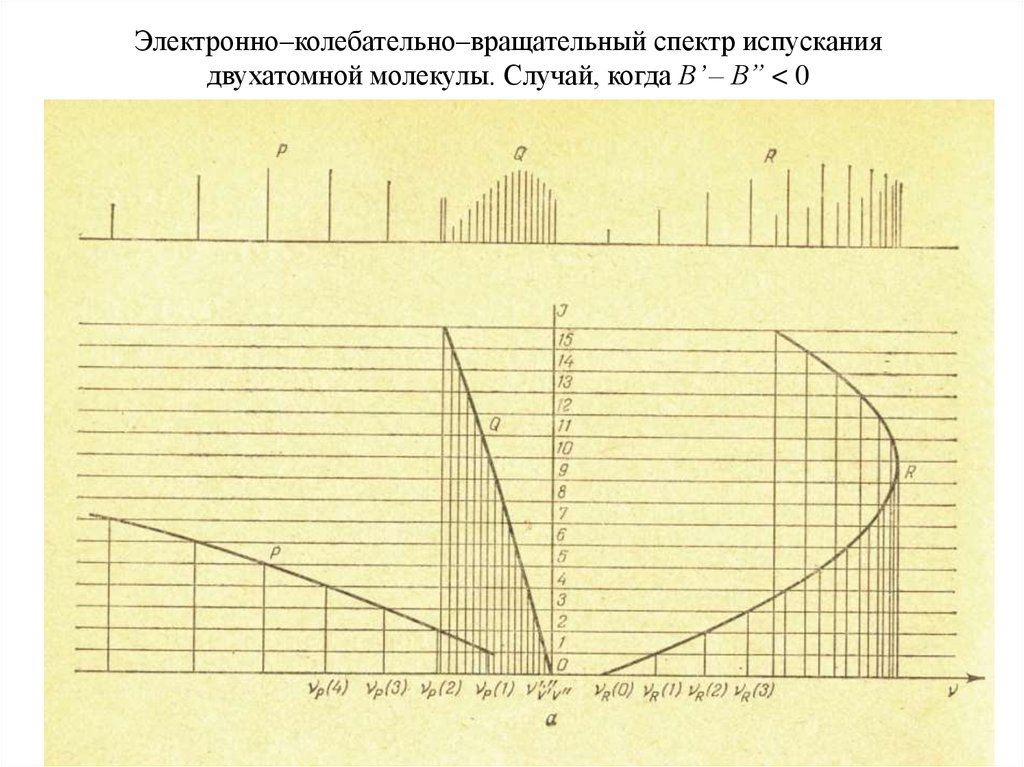
8. Электронно–колебательно–вращательный спектр испускания двухатомной молекулы. Случай, когда B’ – B” < 0

Электронно–колебательно–вращательный спектр испускания
двухатомной молекулы. Случай, когда B’ – B” < 0

9. Электронно–колебательно–вращательный спектр испускания двухатомной молекулы. Случай, когда B’ – B” > 0

Электронно–колебательно–вращательный спектр испускания
двухатомной молекулы. Случай, когда B’ – B” > 0