Similar presentations:
Строение вещества. РГР «Расчёт энергии связи и энергии диссоциации двухатомных молекул спектроскопическим методом»
1.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
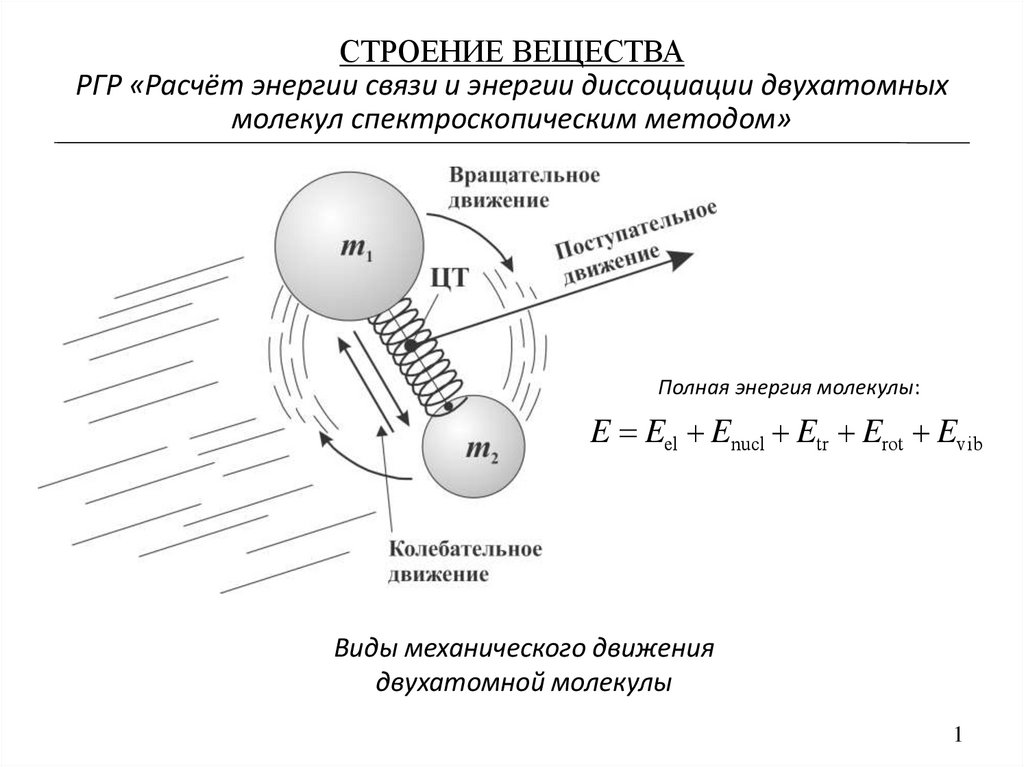
Полная энергия молекулы:
E Eel Enucl Etr Erot Evib
Виды механического движения
двухатомной молекулы
1
2.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
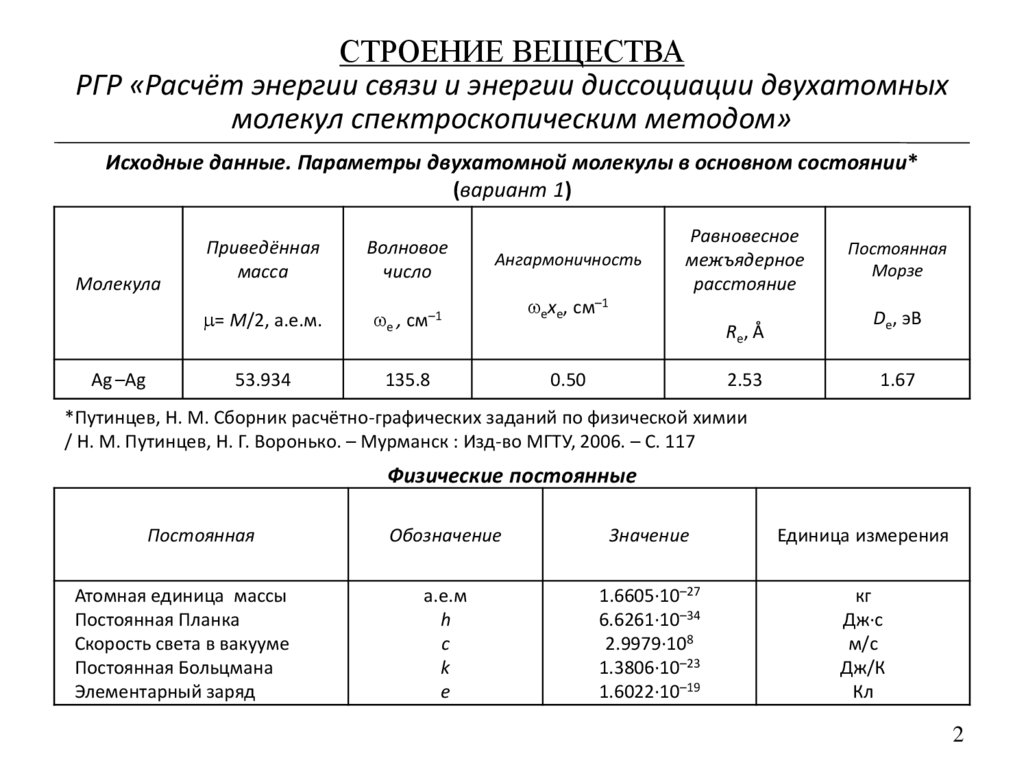
Исходные данные. Параметры двухатомной молекулы в основном состоянии*
(вариант 1)
Молекула
Аg –Ag
Приведённая
масса
Волновое
число
= M/2, а.е.м.
e , см–1
53.934
135.8
Ангармоничность
eхe, см–1
Равновесное
межъядерное
расстояние
R e, Å
0.50
2.53
Постоянная
Морзе
De, эВ
1.67
*Путинцев, Н. М. Сборник расчётно-графических заданий по физической химии
/ Н. М. Путинцев, Н. Г. Воронько. – Мурманск : Изд-во МГТУ, 2006. – C. 117
Физические постоянные
Постоянная
Атомная единица массы
Постоянная Планка
Скорость света в вакууме
Постоянная Больцмана
Элементарный заряд
Обозначение
Значение
Единица измерения
а.е.м
h
с
k
e
1.6605·10–27
6.6261·10–34
2.9979·108
1.3806·10–23
1.6022·10–19
кг
Дж·с
м/с
Дж/К
Кл
2
3.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
1. Определите приведенную массу осциллятора исследуемой частицы.
M Ag M Ag
M Ag
1 а.е.м.
1 а.е.м.
M Ag M Ag
2
107.868
1.6605 10 27 кг 53.934 1.6605 10 27 кг 89.557 10 27 кг
2
2. Найдите величину момента инерции димера.
2
I R 89.557 10
2
e
27
кг 2.53 A 10 10 м 573.25 10 47 кг м 2
3. Рассчитайте значения вращательных постоянных молекулы Вe и Вe .
2
h2
6.626 10 34 Дж с
Be 2 2
9.700 10 25 Дж
47
2
8 I 8 573.25 10 кг м
h
6.626 10 34 Дж с
Be 2
9.766 м 1
4 Ic 4 2 573.25 10 47 кг м 2 2.998 108 м
с
3
4.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
4. Найдите значения энергии молекулы на первых 10-ти вращательных уровнях ротатора
(вращательных квантовых чисел j = 1, 2, …, 10).
Erot j Be j j 1
Erot 1 Be 1 1 1 9.700 10 25 Дж 2 0.194 10 23 Дж
j
1
2
3
4
5
0.194
0.582
1.16
1.94
2.91
j
6
7
8
9
10
Erot(j), Дж·10–23
4.07
5.43
6.98
8.73
10.67
Erot(j), Дж·10–23
4
5.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
5. Найдите значения частот ( rot и rot), соответствующих переходу с квантового уровня
j = 0 на уровень j = 1, 2, …, 10.
rot j j Be j j
rot j j rot j j c
rot 0 1 Be 0 1 9.766 м 1
rot 0 1 9.766 м 1 2.998 108
м
29.28 108 c 1
с
j → j
rot (j → j ), м–1
rot (j → j ), с–1·108
0→1
9.766
29.28
0→2
19.53
58.56
0→3
29.30
87.84
0→4
39.06
117.1
0→5
48.83
146.4
0→6
58.60
175.7
0→7
68.36
205.0
0→8
78.13
234.2
0→9
87.89
263.5
0 → 10
97.66
292.8
5
6.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
6. Найдите значения энергии вращательного движения, исходя из принципа равномерного
распределения энергии по степеням свободы, при температурах 100 и 300 К
(Erot = irotkT/2).
Сравните значения Еrot, полученные из квантово-механических и классических
представлений.
Для определения вращения линейной молекулы требуется знать 2 координаты (irot = 2).
Erot
2kT
kT
2
Дж
100 K 138.1 10 23 Дж
К
Дж
Erot 300 K 1.381 10 23
300 K 414.3 10 23 Дж
К
Erot 100 K 1.381 10 23
Значения Еrot, полученные из квантово-механических представлений (Слайд 4),
на 1 – 3 порядка меньше значений Еrot, полученных из классических представлений.
6
7.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
7. Используя исходные данные найдите величину коэффициента ангармоничности
осциллятора xe и максимальное значение колебательного квантового числа vmax.
e xe 0.50 см 1
xe
3.682 10 3
1
e 135.8 см
1 xe 1 3.682 10 3
v max
135.3 135
3
2 xe
2 3.682 10
8. По собственным частотам колебаний атомов в молекуле ( е и е) и коэффициентам
ангармоничности хе определите длину волны и частоты и , соответствующие
переходам с v0 на v = 1 (основной тон), с v0 на v = 2 (первый обертон),
с v0 на v = 3 (второй обертон) при неизменном электронном состоянии.
Собственная частота колебаний атомов в молекуле (волновое число):
e 135.8 см 1 135.8 10 2 м 1
e e c 135.8 10 2 м 1 2.998 108
м
407.1 1010 с 1
с
7
8.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
8.1. Основной тон (0 → 1):
e 1 2 xe 135.8 10 2 м 1 1 2 3.682 10 3 1.348 10 4 м 1
с 1.348 104 м 1 2.998 108
м
4.041 1012 с 1
с
1
1
7.418 10 5 м
4
1
1.348 10 м
2 1
3
4
1
8.2. Первый обертон (0 → 2): 1 2 e 1 3xe 2 135.8 10 м 1 3 3.682 10 2.686 10 м
1 1с 2.686 10 4 м 1 2.998 108
1
8.3. Второй обертон (0 → 3):
м
8.053 1012 с 1
с
1
1
3.723 10 5 м
4
1
1 2.686 10 м
2 2с 4.014 10 4 м 1 2.998 108
м
12.03 1012 с 1
с
2 3 e 1 4 xe 3 135.8 10 2 м 1 1 4 3.682 10 3 4.014 10 4 м 1
2
1
1
2.491 10 5 м
4
1
2 4.014 10 м
8
9.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
9. Установите участок спектра (инфракрасный, видимый или ультрафиолетовый),
в котором расположены полосы поглощения этих переходов.
Области длин волн различных участков электромагнитного спектра*
*Стромберг А.Г. Физическая химия / А.Г. Стромберг, Д.П. Семченко. – М : Высшая школа, 2001. – C. 46
Полосы поглощения расположены в инфракрасной области электромагнитного спектра
(колебательно-вращательный вид спектра)
9
10.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
10. Определите энергию колебаний молекулы на различных колебательных уровнях,
начиная с колебательных квантовых чисел v 0 и до v = vmax
(если vmax будет большим, то достаточно определить Evib при v = 0, 1, 5, ... , vmax – 1, vmax,
чтобы на графике было около 10 точек). Результат вычислений занести в таблицу.
2
1
1
Evib v v h e v h e xe
2
2
1
Evib 0 0 6.626 10 34 Дж с 407.1 1010 с 1
2
2
1
0 6.626 10 34 Дж с 407.1 1010 с 1 3.682 10 3 1.346 10 21 Дж
2
v
0
1
5
10
30
50
Evib(v), Дж·10–21
1.346
4.024
14.54
27.23
73.03
110.9
v
70
90
110
134 = vmax– 1
135 = vmax
Evib(v), Дж·10–21
140.8
162.8
176.8
183.1
183.2
10
11.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
11. Определите величины постоянных и De потенциала Морзе.
Значение запишите в виде числа в десятой степени.
8 2 e xe
8 2 89.557 10 27 кг 407.1 1010 с 1 3.682 10 3
1.265 1010 м 1
34
h
6.626 10 Дж с
h e 6.626 10 34 Дж с 407.1 1010 с 1
De
183.2 10 21 Дж
3
4 xe
4 3.682 10
12. Сравните значения энергии колебательных переходов (с v 0 на v 1 и с vmax– 1 на v max)
и сделайте вывод о характере зависимости Еvib(v)= f(v).
Evib 0 1 4.024 1.346 10 21 2.678 10 21 Дж
Evib 134 135 183.2 183.1 10 21 0.1 10 21 Дж
Вследствие ангармоничности колебательные уровни энергии с увеличением
колебательного квантового числа v и приближением к границе диссоциации молекулы
(соответствующей бесконечно большому расстоянию между атомами) постепенно
сближаются между собой (сходятся).
Еvib(v) при увеличении v уменьшается. Химическая связь между атомами разрушается.
11
12.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
13. Сравните значения энергии колебательных переходов (с v 0 на v 1 и с vmax– 1 на v max)
с энергией вращательных переходов и с энергией kT при 100 и 300К.
Evib 0 1 4.024 1.346 10 21 2.678 10 21 Дж
Evib 134 135 183.2 183.1 10 21 0.1 10 21 Дж
Erot 1 2 0.582 0.194 10 23 0.388 10 23 0.004 10 21 Дж
Erot 9 10 10.67 8.73 10 23 1.94 10 23 0.194 10 21 Дж
Еvib(0→1) на 1 – 3 порядка превышает Еrot.
Еvib(134→135) сопоставима с Еrot(9→10).
Erot 100 K 1.381 10 21 Дж
Erot 300 K 4.143 10 21 Дж
Еvib(0→1) сопоставима с Еrot(100К) и Еrot(300К).
12
13.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
14. Сравните значение постоянной Морзе Dе с максимальным значением колебательной
энергии Еvib(vmax).
Evib v max 135 De 183.2 10 21 Дж
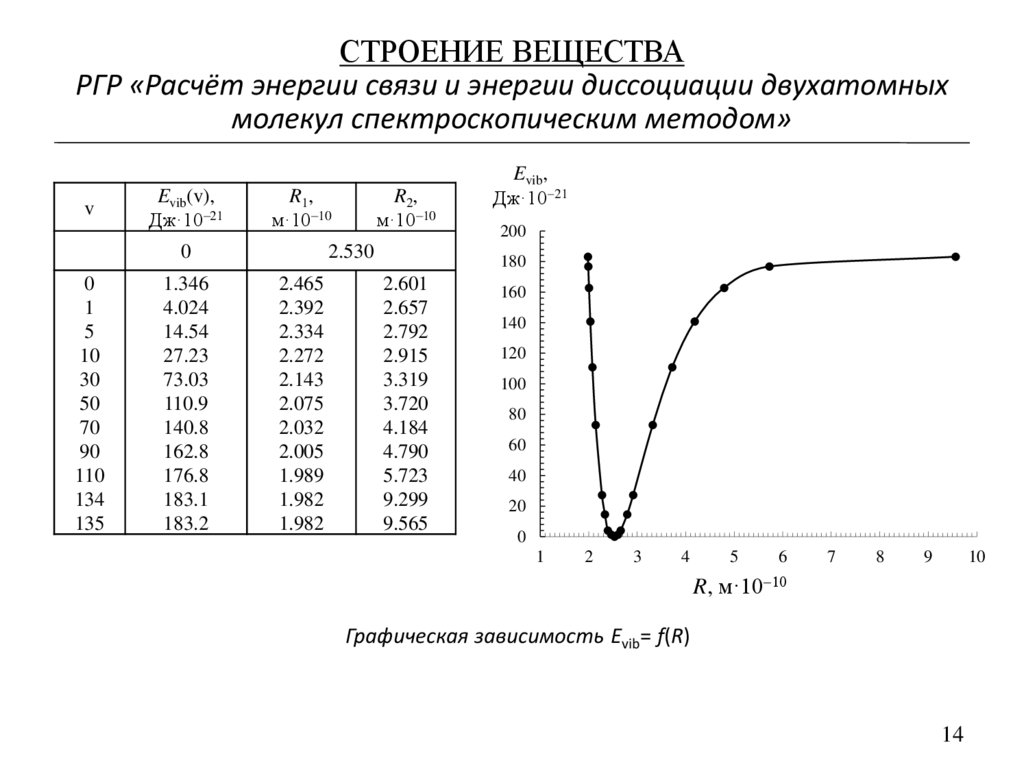
15. Постройте график зависимости Evib= f(R).
Для этого определите значения амплитуды колебания димера R1 и R2.
E 1 2
E 1 2
ln 1 vib
ln 1 vib
De
De
R1 Re
R2 Re
Равновесное состояние: Evib = 0 → R1 = R2 = Re = 2.53·10–10 м
v = 0:
1.346 1 2
ln 1
183.2
2.465 10 10 м
R1 2.53 10 10 м
10 1
1.265 10 м
1.346 1 2
ln 1
183.2
2.601 10 10 м
R2 2.53 10 10 м
10 1
1.265 10 м
13
14.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
v
Evib(v),
Дж·10–21
R1,
м·10–10
0
0
1
5
10
30
50
70
90
110
134
135
1.346
4.024
14.54
27.23
73.03
110.9
140.8
162.8
176.8
183.1
183.2
R2,
м·10–10
2.530
2.465
2.392
2.334
2.272
2.143
2.075
2.032
2.005
1.989
1.982
1.982
Evib,
Дж·10 21
200
180
2.601
2.657
2.792
2.915
3.319
3.720
4.184
4.790
5.723
9.299
9.565
160
140
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
9
10
R, м·10 10
Графическая зависимость Evib= f(R)
14
15.
СТРОЕНИЕ ВЕЩЕСТВАРГР «Расчёт энергии связи и энергии диссоциации двухатомных
молекул спектроскопическим методом»
16. Постройте графики зависимостей Erot= f(j) и Evib= f(v).
Erot,
Дж·10 23
12
10
8
6
4
2
0
1
2
3
4
5
6
7
8
9
10 11 12
Evib,
Дж·10 21
200
180
160
140
120
100
80
60
40
20
0
0
20
40
60
80
100
120
j
Графическая зависимость Erot= f(j)
140
v
Графическая зависимость Evib= f(v)
17. Найдите относительную погрешность метода расчёта энергии связи (в %).
Deрасч Deспр
183.2 10 21 Дж 1.67эВ 160.2 10 21 Кл
100%
100% 31.5%
Deспр
1.67эВ 160.2 10 21 Кл
15












 physics
physics








