Similar presentations:
Многомерная линейная регрессия
1. Многомерная линейная регрессия
Тема 10-1Многомерная линейная
регрессия
Рябева Е.В.
2015
2.
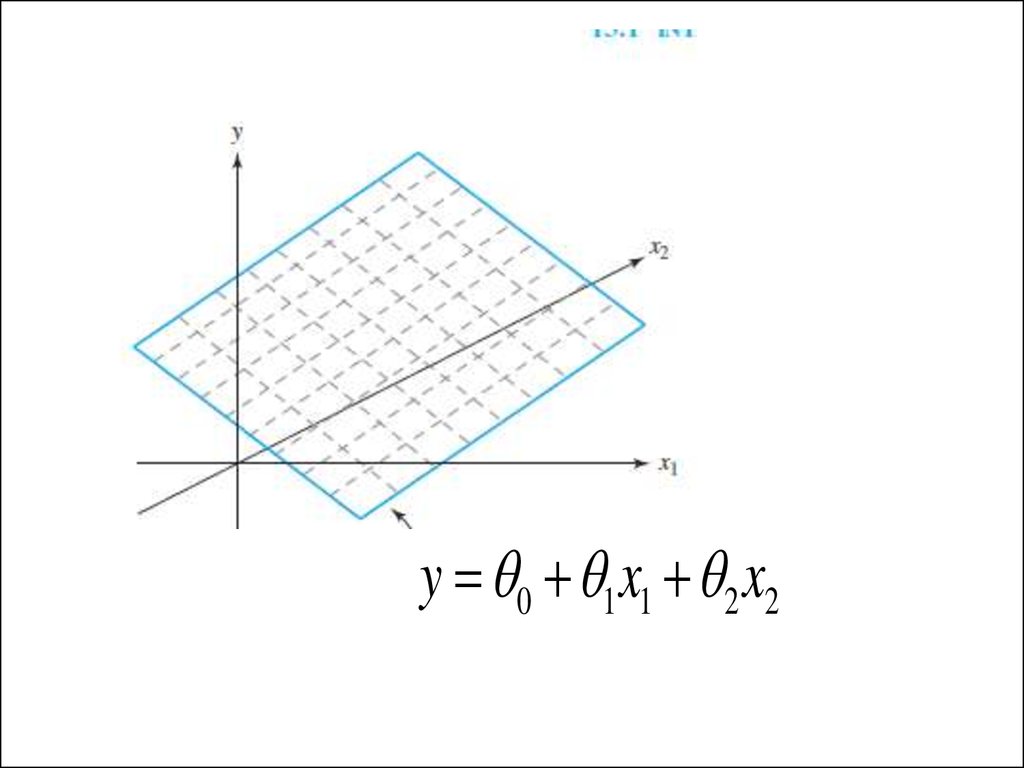
y 0 1 x1 2 x23. Линейная зависимость от нескольких переменных.
yi xi1 1 xi2 2 ... xir r in-число проведенных экспериментов,
Параметров может быть несколько: 1, 2,…, r. r-число
параметров в общем случае может быть произвольно
xi – известные величины (факторы), определяющие i-тый номер эксперим
Имеем линейную зависимость y от параметров θ
1
y1
; y ;
y
r
n
T
Перейдем к
матричной форме
написания
уравнения. Введем
обозначения
1
n
4.
• Запишем систему линейных уравненийв матричном виде
5.
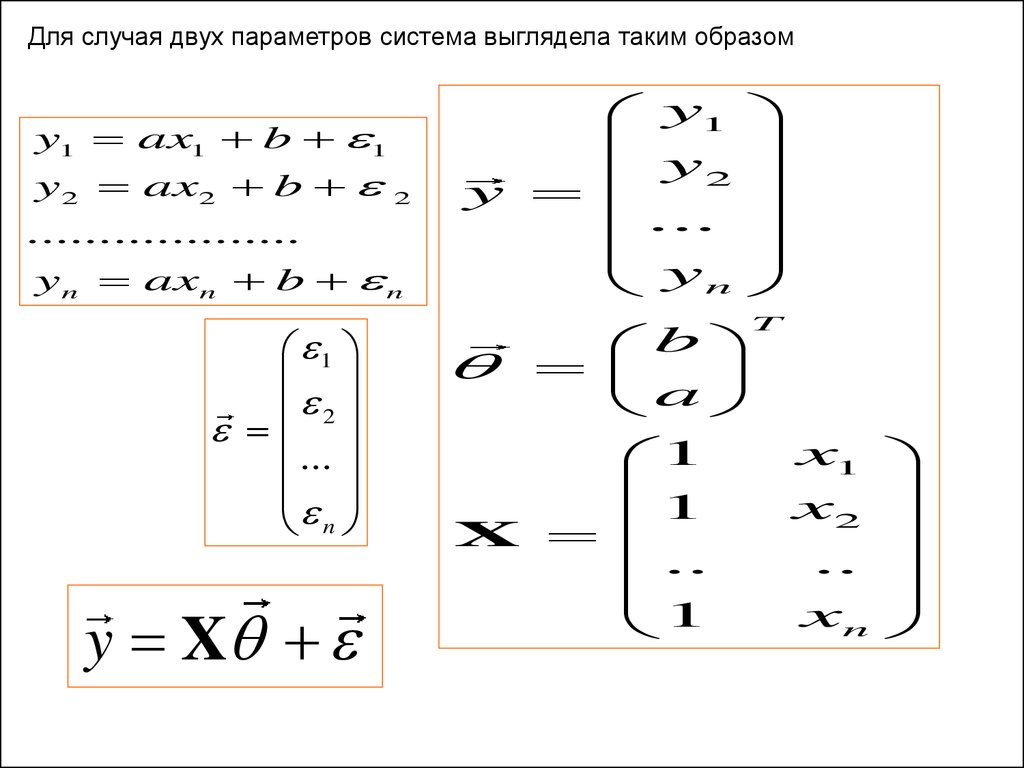
Для случая двух параметров система выглядела таким образомy1 ax1 b 1
y 2 ax2 b
2
...................
y n axn b n
1
2
...
n
y X
y1
y
2
y
...
yn
b
a
1
1
X
..
1
T
x1
x2
..
xn
6.
Для случая r параметров системаy1 x11 1 x12 2 ... x1r r 1
y2 x21 1 x22 2 ... x2 r r 2
..................................................
yn xn1 1 xn 2 2 ... xnr r n
1
2
...
n
y X
y1
y
y 2
...
yn
1
...
r
x11
X
x
n1
T
x1r
xnr
7.
y X 0Эту систему уравнений надо решить относительно , используя
метод максимального правдоподобия и тот факт, что погрешности
измерений yi с дисперсиями i подчиняются нормальному
распределению, т.е.:
2
2
( yi i )
i
1
1
f ( yi )
exp
exp 2
2
2 i
2 i
2 i
i
8.
Функция правдоподобия для n измерений имеет вид:2
n
1
1
i
L f ( yi ) (2 ) ( i ) exp 2
i 1
i 1
2 i 1 i
n
n
2
n
Логарифмическая функция правдоподобия
2
n
n
1
n
l ln L ln 2 ln i 1 i2
2
i 1
2 i 1 i
Это выражение достигает максимума, когда последнее слагаемое будет
минимально.Условие МНК
T
( yi xi )2
Q
min
2
i
i 1
i 1
n
2
i
2
i
n
Как записать i, используя введённые матричные обозначения
T
y x 0 y x i yi xi
Введём вектор-столбец
xi ( xi1 , xi2 ...xir )
9.
матрица ошибок.12
2
0 2
C y Cε
0
0
n2
Обратная ей матрица называется весовой:
gi
1
i2
g1
G y = Gε
0
1
0 12
gn
0
0
1
n2
С учётом введённых обозначений для Gy можно переписать
T
i2
Q 2 G y min
i 1 i
n
или
Q ( y X ) Gy ( y X ) min
T
10.
Для получения min необходимо образовать частные производные Q поi и приравнять их к 0.
T
xT
Q
0 ; i=1...r
i
T
T
T
Q
T
Gy
G y x G y G y x x T G y x T G y 2x T G y
2x TG y ( y x ) 0
x T G y y x T G y x
Для получения искомой оценки параметра
необходимо подействовать оператором
(x Gy x) x Gy y
T
-1
T
T
(x Gy x)
-1
Оценка параметров θ МНК
линейный случай
11.
Оценка дисперсии оценок параметровДисперсия элементов вектора оценок (ковариационная
матрица оценок параметров) то же может быть записана в
векторном виде
var( ) C y 2 (X T X) -1
Дисперсию y можно оценить как и двухмерном случае суммой квадратов
отклонений от выровненной (рассчитанной) поверхности
n
r
1
S
( yi ( xij j ))
n r 1 i 1
j 1
2
y
2
2
y
диагональные
элементы этой
матрицы- дисперсии
оценок
S i C i,i
2
12.
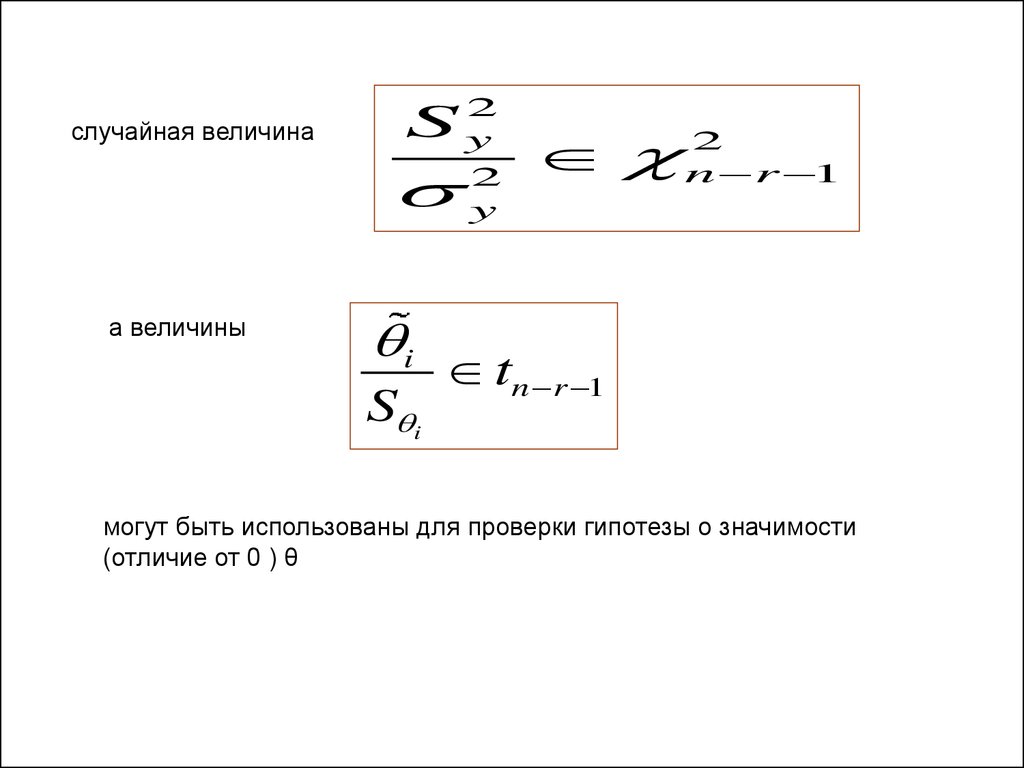
случайная величина2
Sy
а величины
i
S i
2
y
n2 r 1
tn r 1
могут быть использованы для проверки гипотезы о значимости
(отличие от 0 ) θ
13. Пример 10-4 на многомерный МНК- потребление –производство –градус-дней
Пример 10-4на многомерный МНКпотребление –производство –
градус-дней
14.
15.
16.
( x Gy x) x Gy yT
1 T
Рассмотрим применение этой оценка к простым случаям
Случай простой линейной регрессии
Зависимость от двух параметров θ0 и θ1 и одной переменной х
y= θ0 + θ1x
Пусть произвели только 2 измерения
y1 x11 1 0
y2 x12 1 0
Можно представить задание в матричной форме:
x11
x
x12
1
1
y1
( 0 , 1 )
y
y2 Решение для
простой линейной
регрессии в
матричном виде
x10 1
x20 1
x x xT y
T
1
17.
Оценить для прямых неравноточных измерений.В этом случае: yi = + i i = 1,…n.
( x Gy x) x Gy y
1 T
T
; x0 0 ;
1
1
x
1
g1
Gy
gn
gi
1
i2
1
y1
1 n
n
g
g
1
1
1
1,1...1
1,1...1
gi g i yi
gn
g n i 1 i 1
yn
1














 mathematics
mathematics








