Абсолютные и относительные показатели (величины)

1.

ЛЕКЦИЯ
Дисциплина «ПРАВОВАЯ СТАТИСТИКА»
Тема № 4-1:
«Абсолютные и относительные
показатели, средние величины»
Кафедра Управления и информационно-технического
обеспечения деятельности УИС
ОЗЁРСКИЙ СЕРГЕЙ ВЛАДИМИРОВИЧ, к.ф.-м.н., доцент
САМАРА 2014

2. План лекции

1.
Абсолютные и относительные
показатели (величины).
2.
Средние величины.

3. Статистические показатели

Статистический показатель – это
количественная характеристика социальноэкономического явления или процесса,
вычисленная с учётом их качественных
характеристик
В отличие от признака статистический
показатель, чаще всего, получается
путем расчета

4.

Статистические показатели в зависимости от
способа их вычисления подразделяются на:
Абсолютные –
•Это суммарные обобщающие
показатель, характеризующие
размеры изучаемых явлений в
конкретных условиях места и
времени.
•Это исходная, первичная,
самая общая форма
выражения СП; числа, взятые
из таблиц без преобразований.
•Это именованные величины,
выраженные через единицы
измерения
Относительные –
•Представляют собой
производные обобщающие
показатели, получаемые в
результате деления одних
абсолютных показателей на
другие.
•Позволяют провести сравнение
различных показателей.
•Как правило, измеряются в
безразмерных коэффициентах
или процентах.

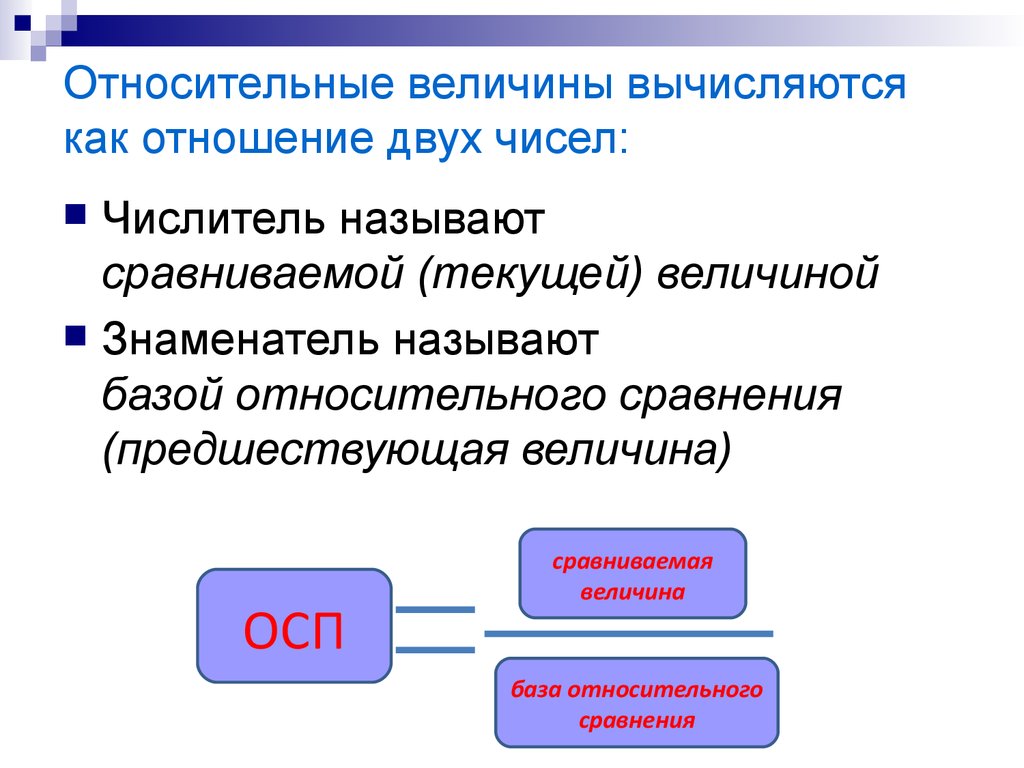
5. Относительные величины вычисляются как отношение двух чисел:

Числитель называют
сравниваемой (текущей) величиной
Знаменатель называют
базой относительного сравнения
(предшествующая величина)
сравниваемая
величина
ОСП
база относительного
сравнения

6. Средние величины

Средняя величина – это обобщающий показатель,
характеризующий значение признака, вокруг которого
концентрируются наблюдения.
Различают следующие средние величины:
Структурные средние величины
(медиана, мода и др.)
Аналитические средние величины
(средняя степенная)

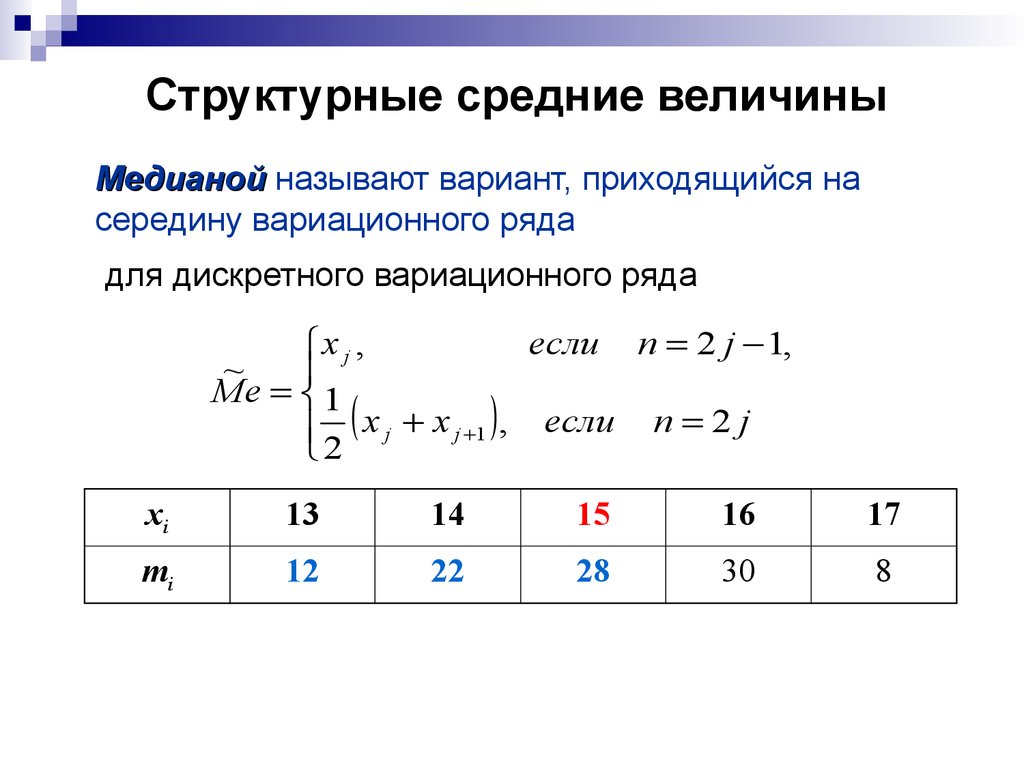
7. Структурные средние величины

Медианой называют вариант, приходящийся на
середину вариационного ряда
для дискретного вариационного ряда
если n 2 j 1,
x j ,
~
Me 1
x j x j 1 , если n 2 j
2
xi
13
14
15
16
17
mi
12
22
28
30
8

8. Структурные средние величины

для интервального вариационного ряда
~
Me xmin
iMe 1
1 k
mi mi
2
i 1
d i 1
;
mMe
где d xmax xmin
- ширина медианного интервала
xi
100-120
120-140
140-160
160-180
mi
9
16
11
4

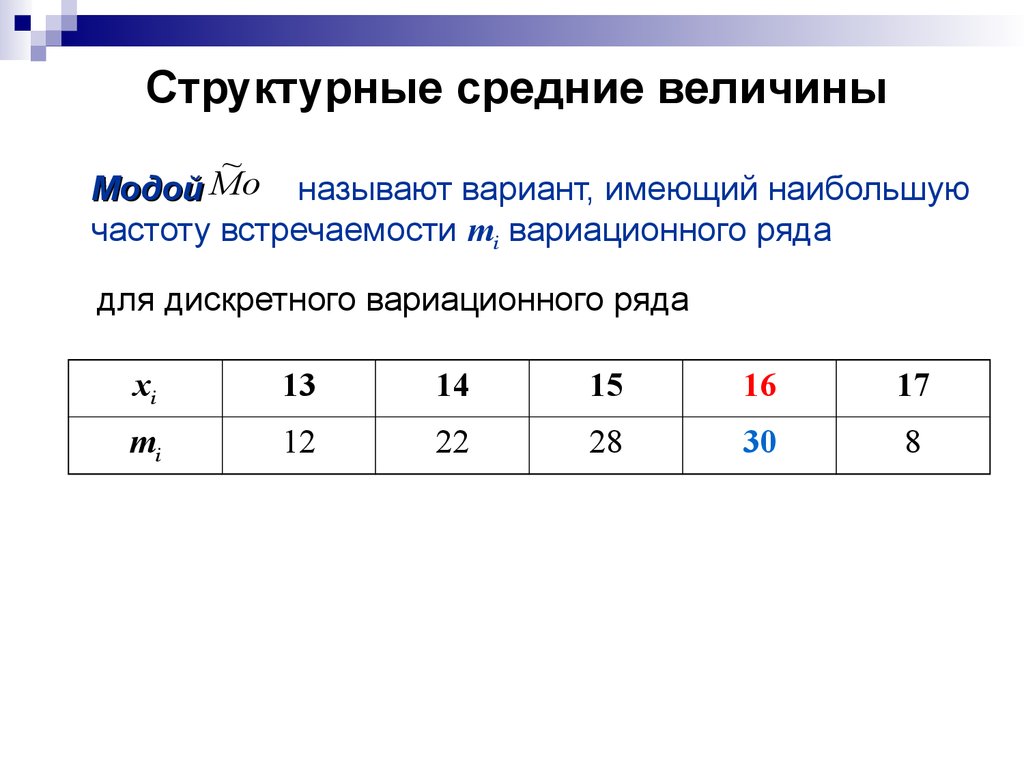
9. Структурные средние величины

~
Модой Mo называют вариант, имеющий наибольшую
частоту встречаемости mi вариационного ряда
для дискретного вариационного ряда
xi
13
14
15
16
17
mi
12
22
28
30
8

10. Структурные средние величины

для интервального вариационного ряда
~
Mo xmin d
где
mMo mMo 1
;
mMo mMo 1 mMo mMo 1
d xmax xmin
- ширина модального интервала
xi
100-120
120-140
140-160
160-180
mi
9
16
11
4

11. Аналитические средние величины

Средняя степенная
1
x1 x2 xn
;
x
n
= 1 – средняя арифметическая;
= -1 – средняя гармоническая;
= 0 – средняя геометрическая;
= 2 – средняя квадратическая.

12. Аналитические средние величины

Средняя арифметическая величина
n
x1 x2 xn
x
n
x
i
i 1
;
n
Средняя арифметическая взвешенная
k
x1m1 x2 m2 xk mk
x
m1 m2 mk
xm
i 1
k
i
i
m
i 1
i
;

13. Аналитические средние величины

Средняя геометрическая величина
g n x1 x2 xn n
n
x ;
i
i 1
Средняя геометрическая взвешенная
g x x x
n
m1
1
m2
2
mk
k
n
k
x
i 1
mi
i
;

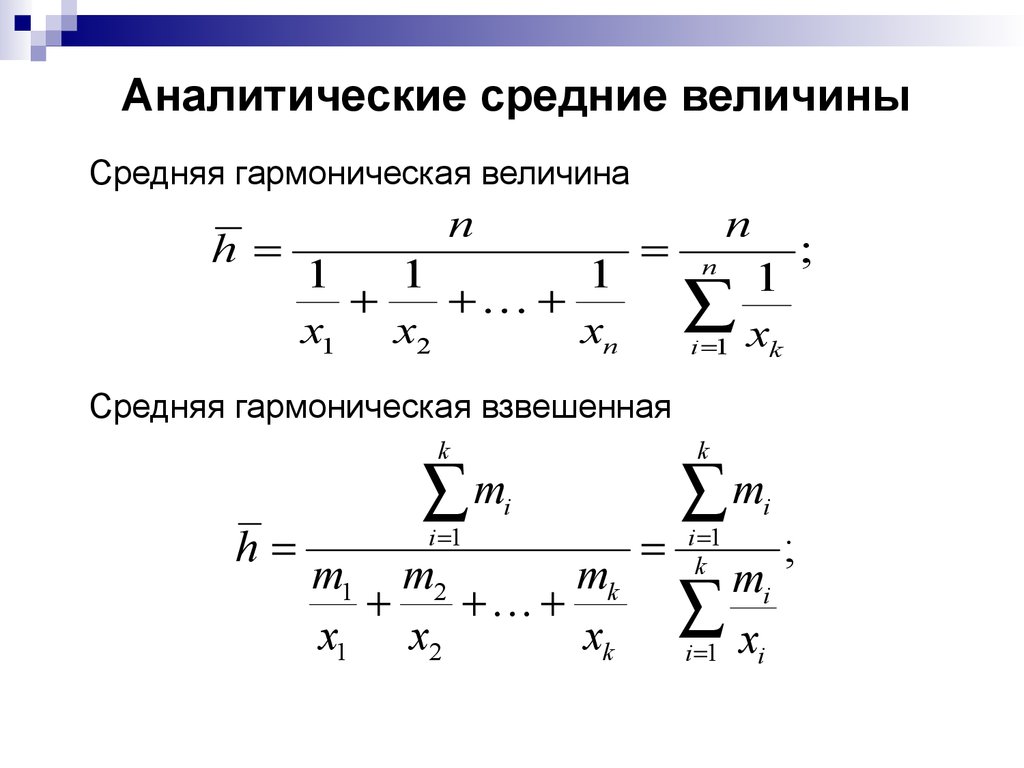
14. Аналитические средние величины

Средняя гармоническая величина
h
n
1
1
1
x1 x2
xn
n
;
n
1
i 1 xk
Средняя гармоническая взвешенная
k
h
m
i 1
i
m1 m2
mk
x1 x2
xk
k
m
i 1
k
i
mi
i 1 xi
;

15. Аналитические средние величины

Средняя квадратическая величина
n
s
2
x
i
x12 x22 xn2
n
i 1
n
Средняя квадратическая взвешенная
k
s
x12 m1 x22 m2 xk2 mk
m1 m2 mk
2
x
i mi
i 1
k
m
i 1
i
;
;

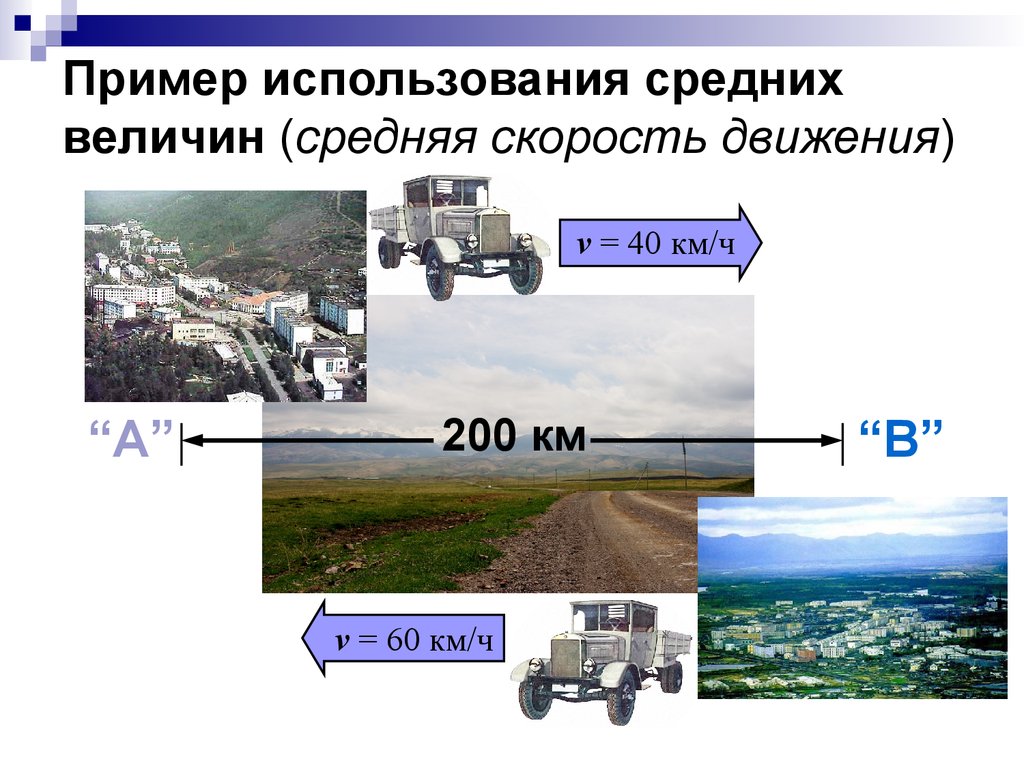
16. Пример использования средних величин (средняя скорость движения)

v = 40 км/ч
“A”
200 км
v = 60 км/ч
“B”

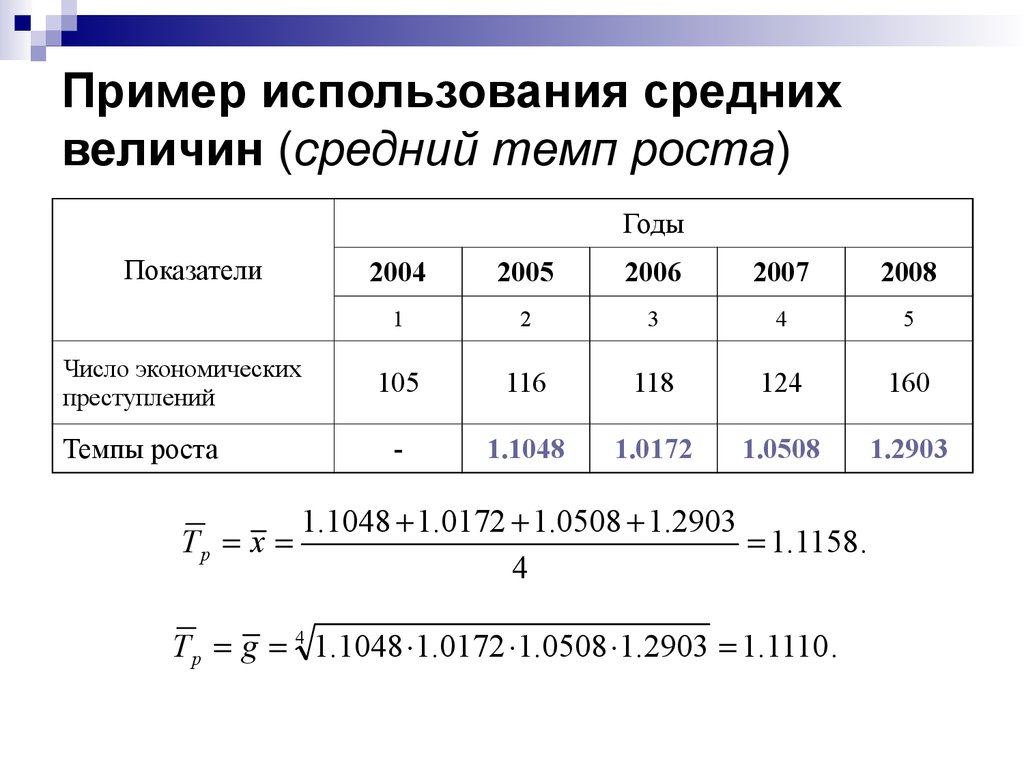
17. Пример использования средних величин (средний темп роста)

Годы
Показатели
Число экономических
преступлений
Темпы роста
2004
2005
2006
2007
2008
1
2
3
4
5
105
116
118
124
160
-
1.1048
1.0172
1.0508
1.2903
1.1048 1.0172 1.0508 1.2903
Tp x
1.1158 .
4
T p g 4 1.1048 1.0172 1.0508 1.2903 1.1110 .

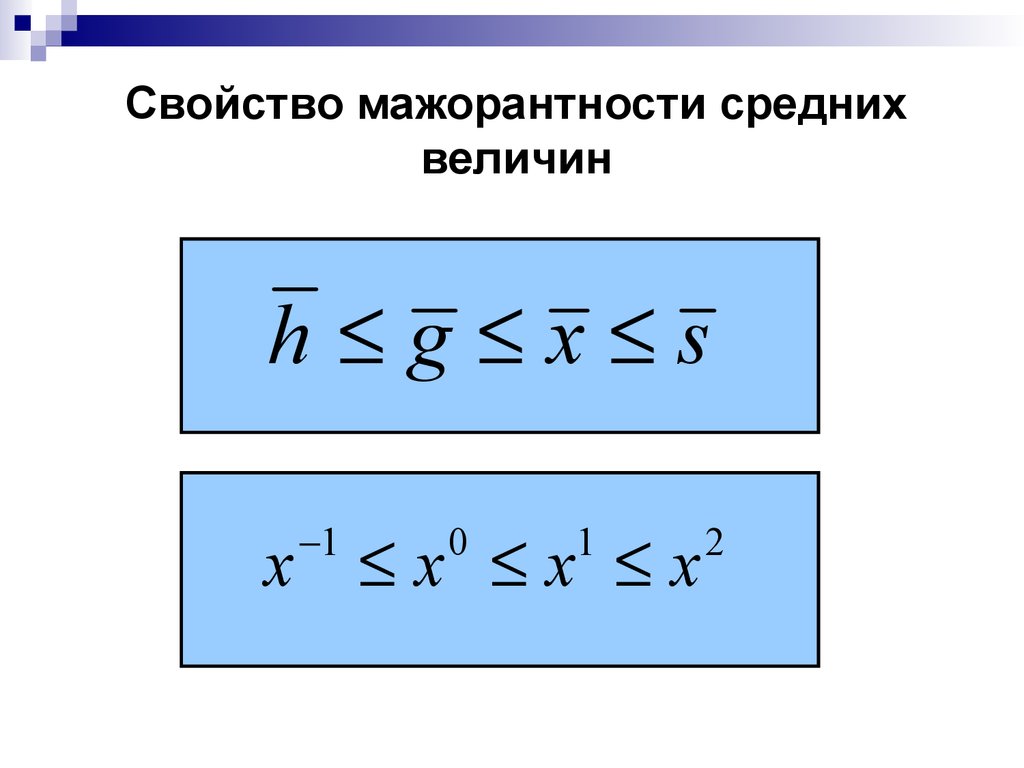
18. Свойство мажорантности средних величин

h g x s
1
x x x x
0
1
2

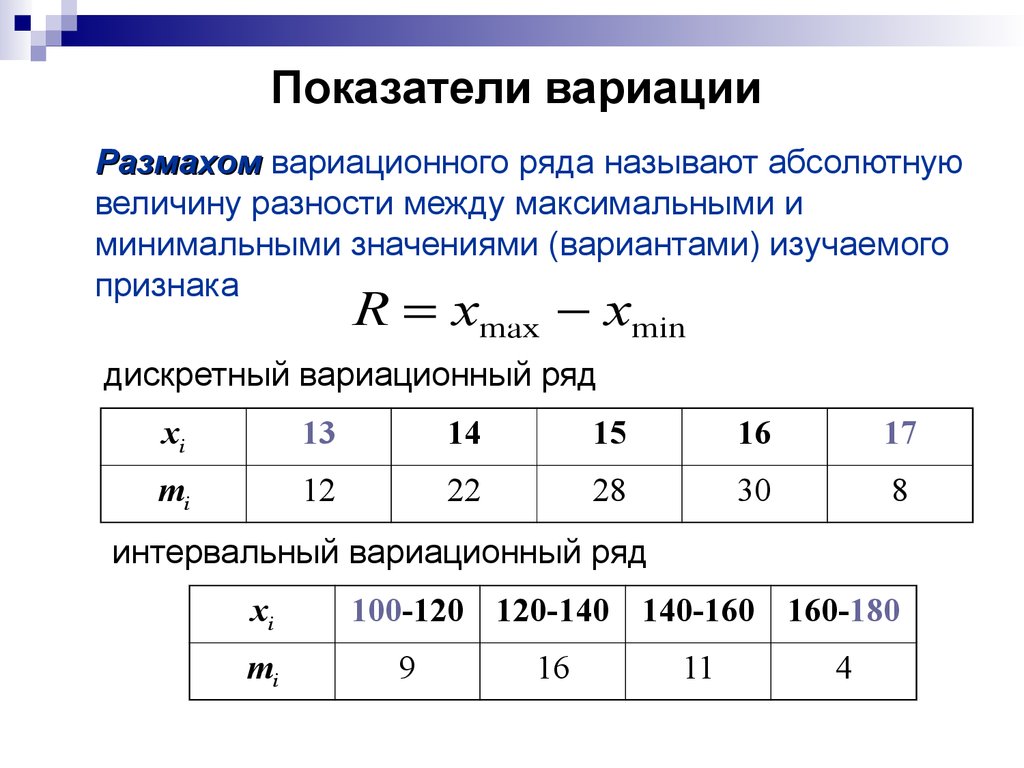
19. Показатели вариации

Размахом вариационного ряда называют абсолютную
величину разности между максимальными и
минимальными значениями (вариантами) изучаемого
признака
R xmax xmin
дискретный вариационный ряд
xi
13
14
15
16
17
mi
12
22
28
30
8
интервальный вариационный ряд
xi
mi
100-120 120-140 140-160 160-180
9
16
11
4

20. Показатели вариации

Средним линейным отклонением вариационного
ряда называют среднюю арифметическую абсолютных
величин отклонений вариантов от их средней
арифметической
k
x1 x m1 x2 x m2 xk x mk
d
m1 m2 mk
x xm
i 1
i
i
k
m
i 1
i

21. Показатели вариации

Дисперсией вариационного ряда называют
среднюю арифметическую квадратов отклонений
вариантов от их средней арифметической
k
s
2
x1 x
2
m1 x2 x m2 xk x mk
m1 m2 mk
2
учитывая, что
wi
2
mi
k
m
i 1
2
x
x
mi
i
i 1
k
m
i 1
, получим:
i
i
k
s x1 x w1 x2 x w2 xk x wk xi x wi
2
2
2
2
i 1
2

22. Показатели вариации

Среднее квадратическое отклонение:
k
s
s2
x
i 1
x mi
2
i
k
m
i 1
i
Коэффициент вариации:
s
100%
x
x 0 .
.

23. Понятие генеральной и выборочной совокупности

Совокупность всех мысленно возможных
объектов того или иного вида, над которыми
проводятся наблюдения с целью получения
конкретных значений определённой случайной
величины, или совокупность результатов всех
мыслимых наблюдений, проводимых при
неизменных условиях над одной из случайных
величин, связанных с данным видом объектов,
называют генеральной совокупностью.

24. Понятие генеральной и выборочной совокупности

Часть отобранных объектов из генеральной
совокупности (результаты наблюдений над
ограниченным числом объектов из этой
совокупности) называется выборочной
совокупностью или просто выборкой.

25. Способы отбора статистических данных

Собственно случайный отбор, при котором объекты
выбираются путём жеребьевки.
Механический отбор, при котором генеральную
совокупность «механически» делят на столько групп, сколько
объектов должно войти в выборку, а из каждой группы
выбирают один объект.
Cерийный отбор, при котором объекты отбираются из
генеральной совокупности не по одному, а сериями, которые
подвергаются сплошному обследованию.
Типический (районированный) отбор, при котором
объекты отбираются не из всей генеральной совокупности, а
из каждой ее типической (однородной) части.

26. Основные характеристики генеральной и выборочной совокупности

Генеральная
совокупность
Выборочная
совокупность
Объём совокупности
N
n
Кол. единиц, обладающих
заданным признаком
M
m
Характеристика
Доля единиц, обладающих
заданным признаком
Среднее значение
Дисперсия
Среднее квадратическое
отклонение
2
х
х
p
M
N
W
x
xi
N
xi
~
x
n
(х
i
x)2
N
(х
i
x)2
N
2
~
х
m
n
(х
~х
~
x )2
i
n
(х
i
~
x )2
n

27. Основные характеристики генеральной и выборочной совокупности

Характеристика
Дисперсия доли
Среднее квадратическое
отклонение доли
Генеральная
совокупность
p2 pq
p
pq
Выборочная
совокупность
W2 W (1 W )
W W (1 W )

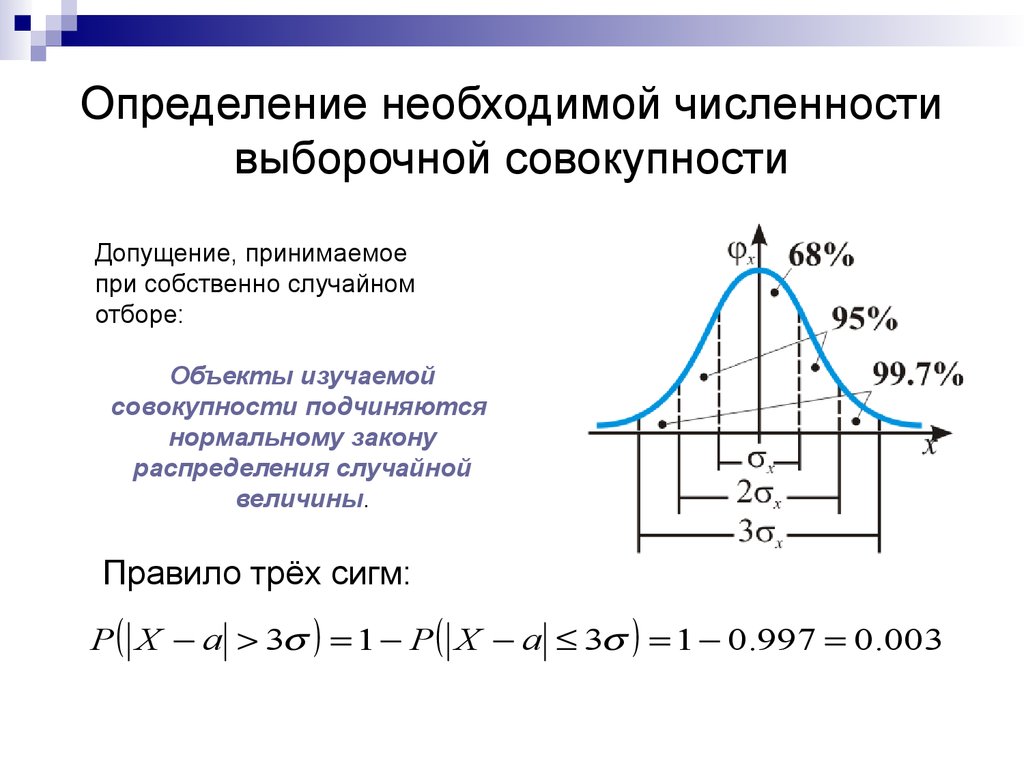
28. Определение необходимой численности выборочной совокупности

Допущение, принимаемое
при собственно случайном
отборе:
Объекты изучаемой
совокупности подчиняются
нормальному закону
распределения случайной
величины.
Правило трёх сигм:
P X a 3 1 P X a 3 1 0.997 0.003

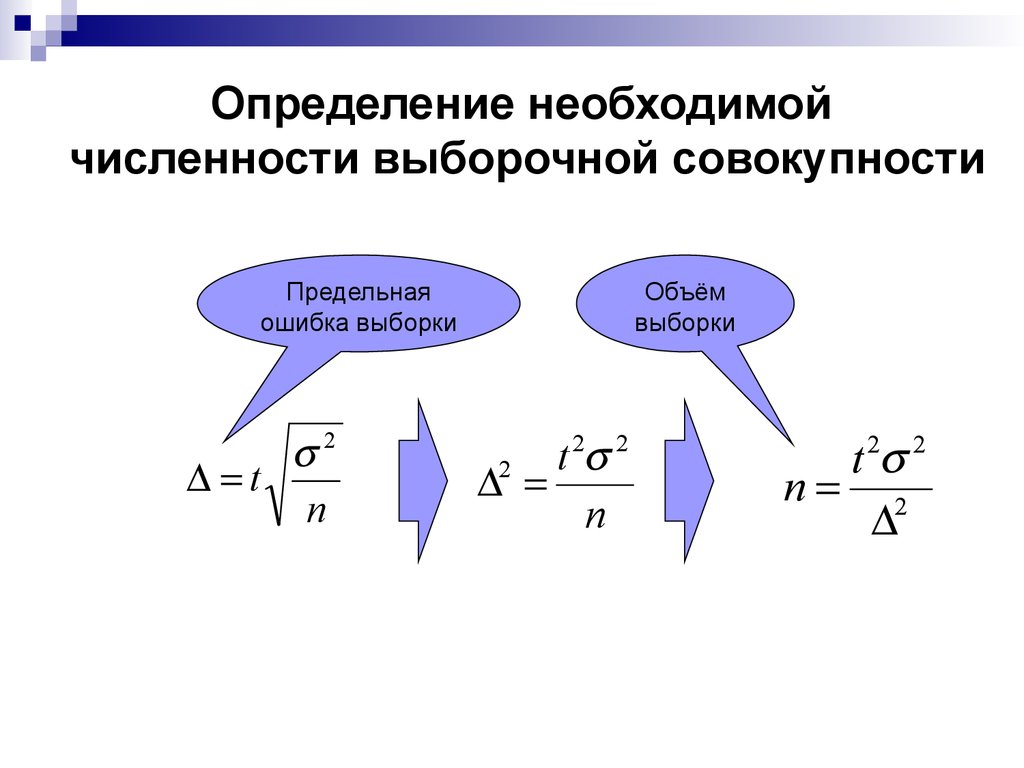
29. Определение необходимой численности выборочной совокупности

Предельная
ошибка выборки
2
t
n
Объём
выборки
2 2
t
2
n
t
n 2
2
2

30. Определение необходимой численности выборочной совокупности

Пример. Для определения среднего возраста 50 тыс.
человек, совершивших экономические преступления в
России, необходимо провести выборочное
обследование методом механического отбора. При
проведении предыдущего подобного обследования
2
величина дисперсии составила ~x = 75. Определите
необходимую численность выборки, чтобы с
вероятностью 0.997 предельная ошибка выборки не
превышала бы x 2.5 года.

31. Определение необходимой численности выборочной совокупности

Решение. Для данной численности N = 50 000 чел.
и величины доверительной вероятности = 0.997,
имеем t = 3. Используя формулу для определения
необходимой численности выборки, получаем:
t
3 75
nx 2
108.
2
x
2.5
2
2
~
x
2
Ответ. Необходимая численность выборки составляет
108 чел.