63_Стереометрия_многогранники_Пирамида

1.

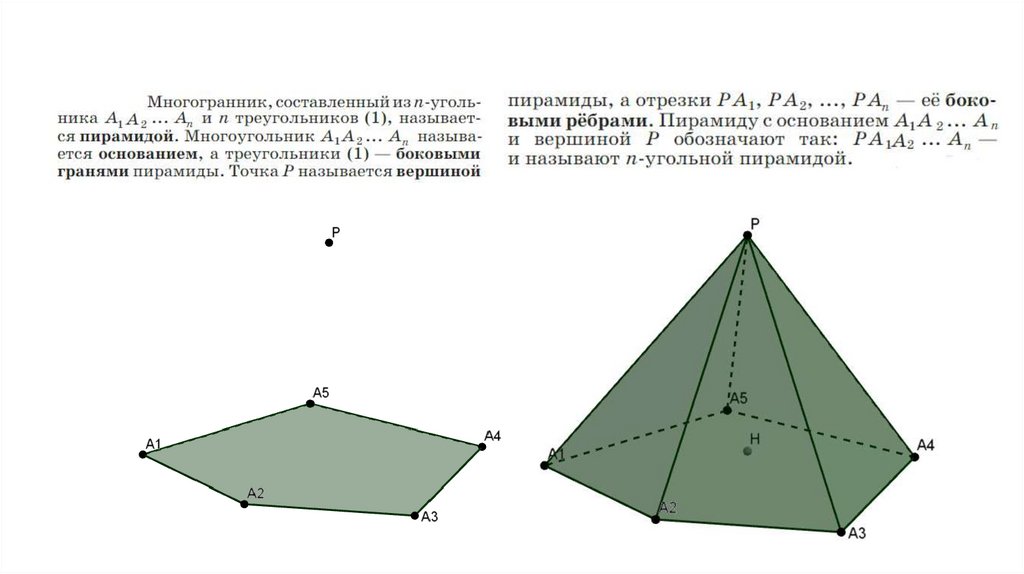
ПИРАМИДА

2.

3.

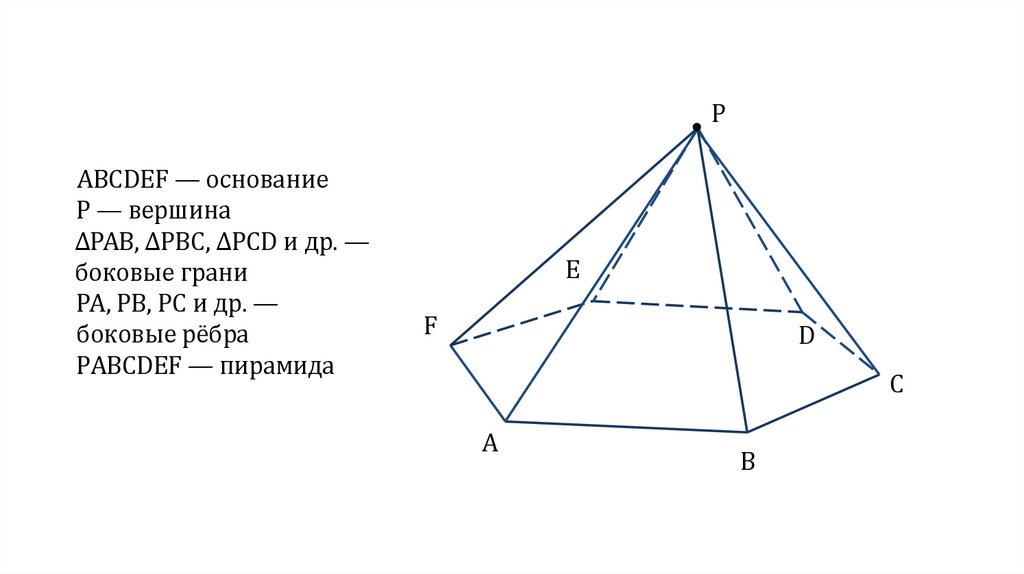
P
ABCDEF — основание
Р — вершина
∆РАВ, ∆РВС, ∆РСD и др. —
боковые грани
РА, РВ, РС и др. —
боковые рёбра
РABCDEF — пирамида
E
F
D
С
А
В

4.

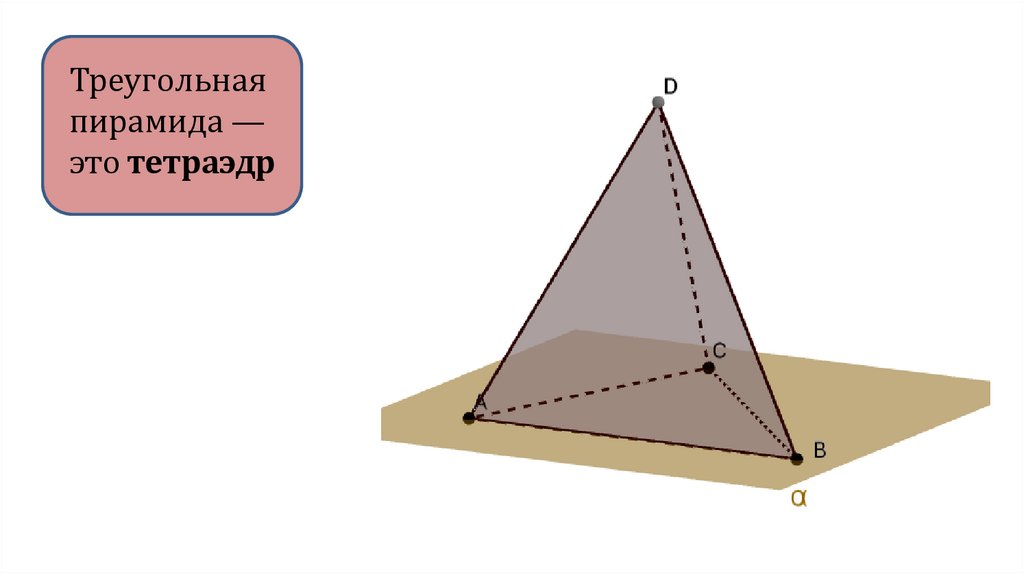
Треугольная
пирамида —
это тетраэдр

5.

6.

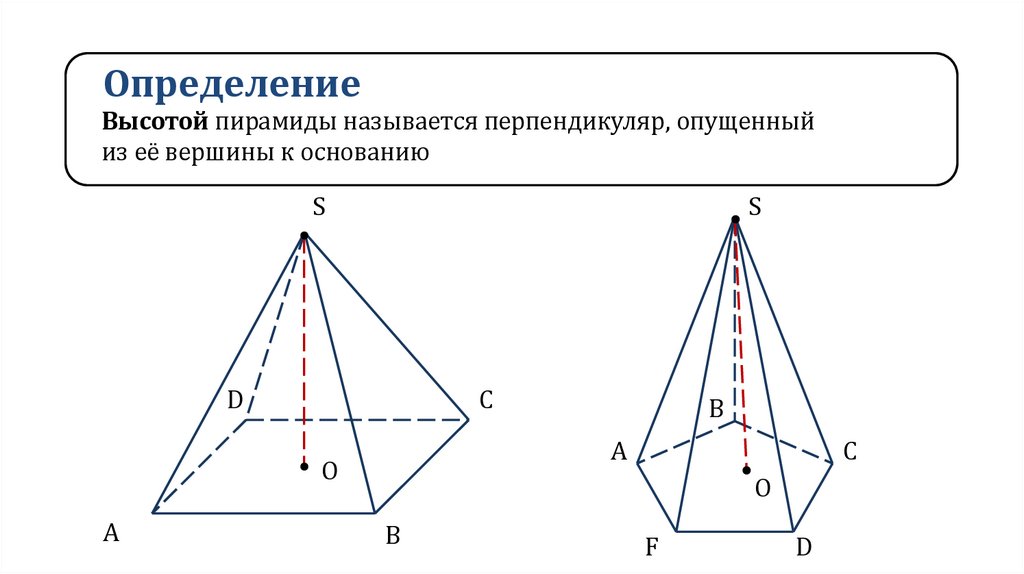
Определение
Высотой пирамиды называется перпендикуляр, опущенный
из её вершины к основанию
S
S
D
С
А
O
А
В
С
O
В
F
D

7.

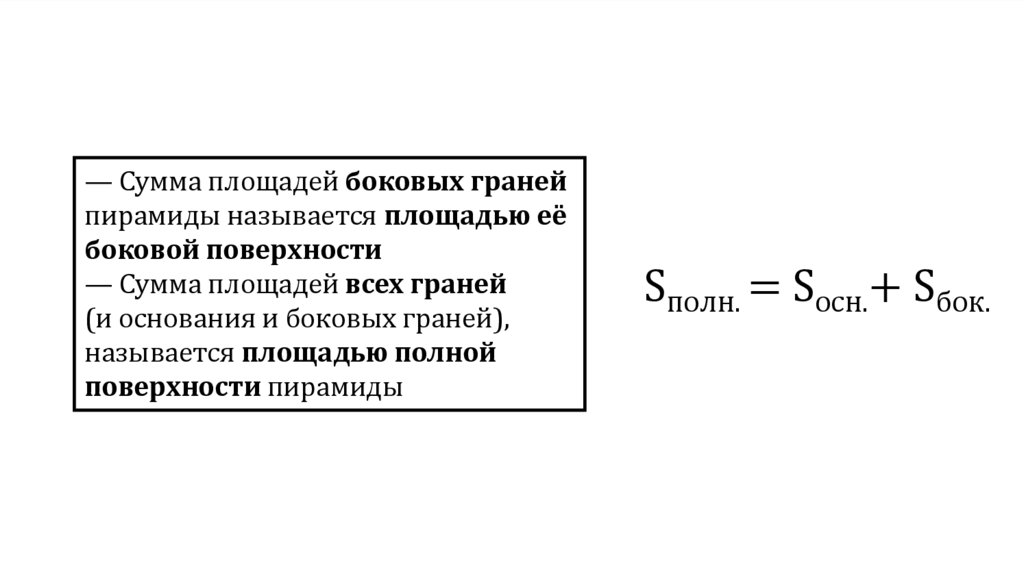
— Сумма площадей боковых граней
пирамиды называется площадью её
боковой поверхности
— Сумма площадей всех граней
(и основания и боковых граней),
называется площадью полной
поверхности пирамиды
Sполн. = Sосн.+ Sбок.

8.

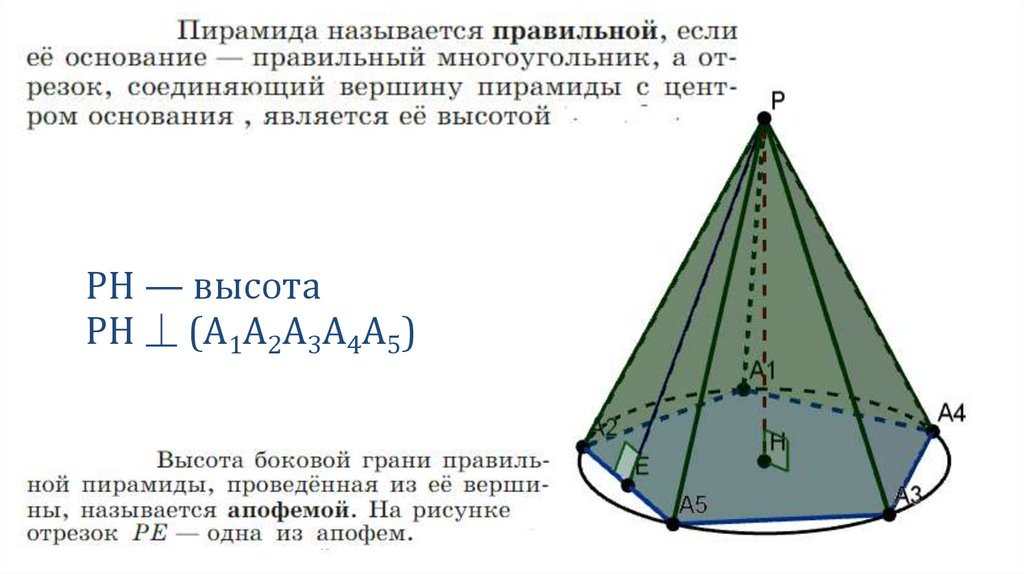
PH — высота
PH ⏊ (A1A2A3A4A5)

9.

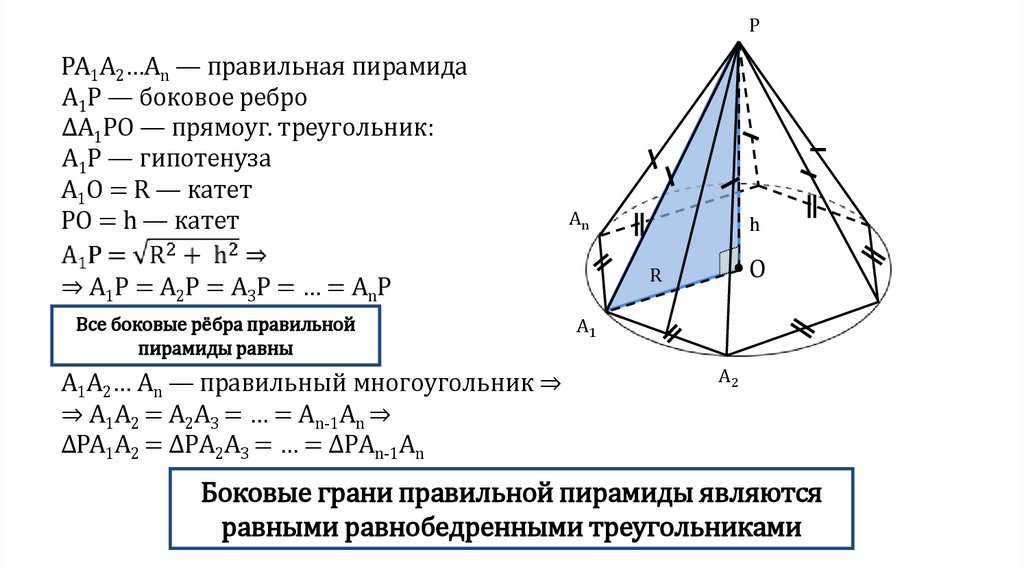
P
PA1A2…An — правильная пирамида
А1Р — боковое ребро
ΔА1РО — прямоуг. треугольник:
А1Р — гипотенуза
А1О = R — катет
РO = h — катет
An
A1A2… An — правильный многоугольник ⇒
⇒ A1A2 = А2А3 = … = Аn-1An ⇒
ΔPA1A2 = ΔPА2А3 = … = ΔPАn-1An
О
R
⇒ A1P = A2P = A3P = … = AnP
Все боковые рёбра правильной
пирамиды равны
h
A1
A2
Боковые грани правильной пирамиды являются
равными равнобедренными треугольниками

10.

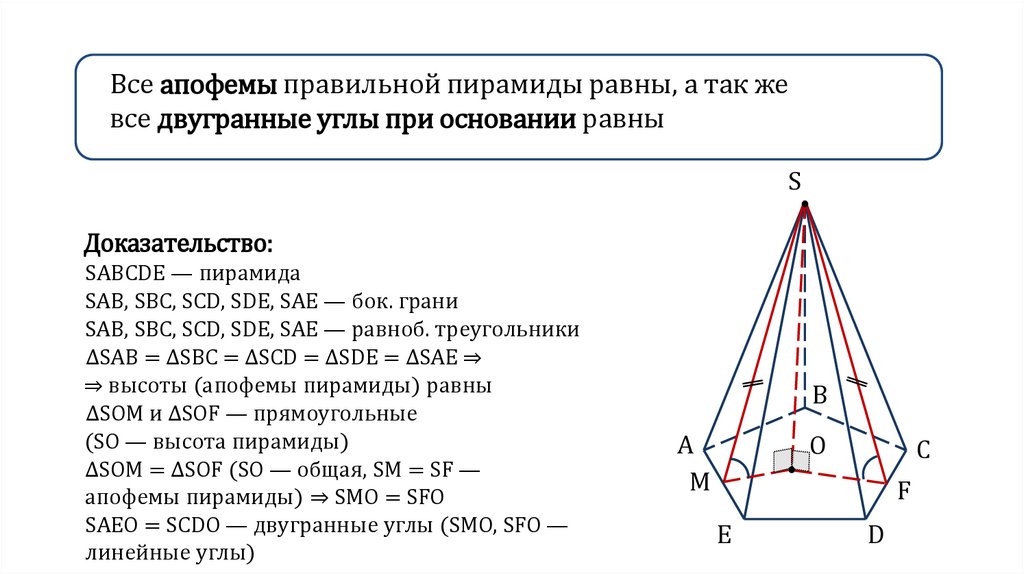
Все апофемы правильной пирамиды равны, а так же
все двугранные углы при основании равны
S
Доказательство:
SABCDE — пирамида
SAB, SBC, SCD, SDE, SAE — бок. грани
SAB, SBC, SCD, SDE, SAE — равноб. треугольники
ΔSAB = ΔSBC = ΔSCD = ΔSDE = ΔSAE ⇒
⇒ высоты (апофемы пирамиды) равны
ΔSОМ и ΔSОF — прямоугольные
(SO — высота пирамиды)
ΔSОМ = ΔSОF (SO — общая, SM = SF —
апофемы пирамиды) ⇒ SMO = SFO
SAEO = SCDO — двугранные углы (SMO, SFO —
линейные углы)
В
А
M
O
С
F
E
D

11.

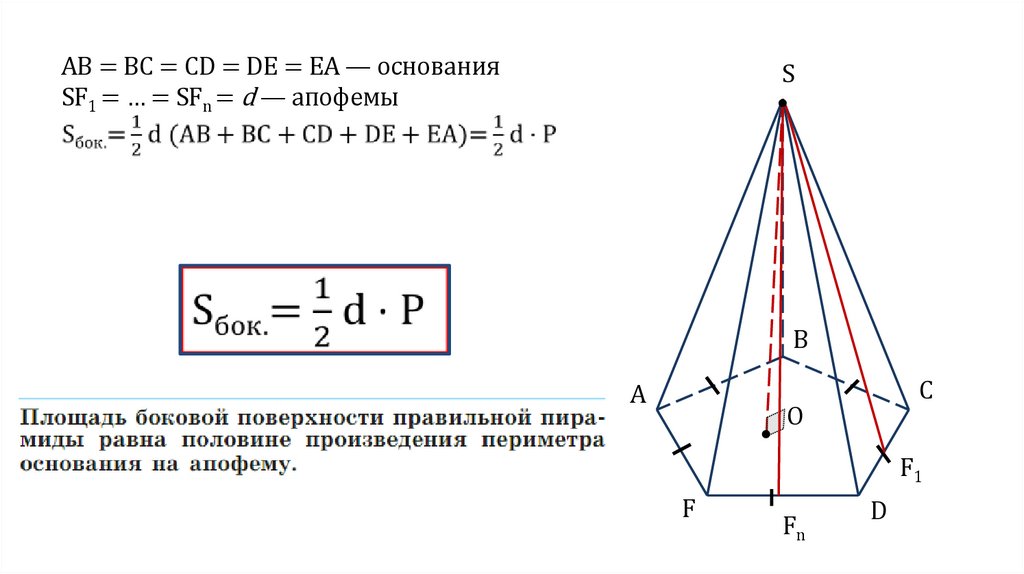
АВ = ВС = CD = DE = EA — основания
SF1 = … = SFn = d — апофемы
S
В
А
С
O
F1
F
Fn
D

12.

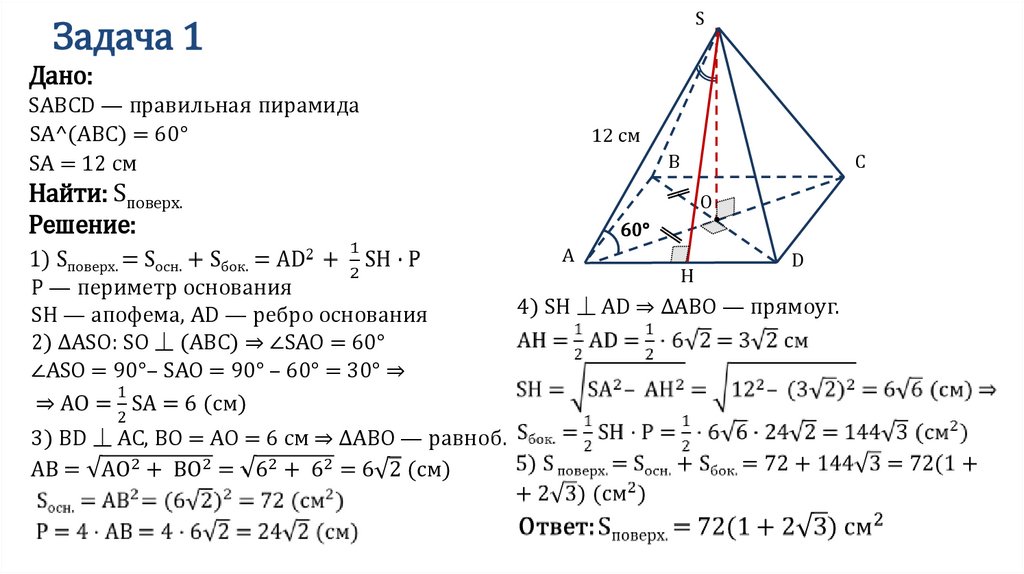
S
Задача 1
Дано:
SABCD — правильная пирамида
SA^(ABC) = 60°
SA = 12 см
12 см
B
Найти: Sповерх.
Решение:
C
O
60°
A
P — периметр основания
SH — апофема, AD — ребро основания
2) ∆ASO: SO ⏊ (ABC) ⇒ ∠SAO = 60°
∠ASO = 90°– SAO = 90° – 60° = 30° ⇒
3) BD ⏊ AC, BO = AO = 6 см ⇒ ∆ABO — равноб.
H
D
4) SH ⏊ AD ⇒ ∆ABO — прямоуг.