Similar presentations:
Призма. Пирамида
1. Определение призмы, пирамиды.
2.
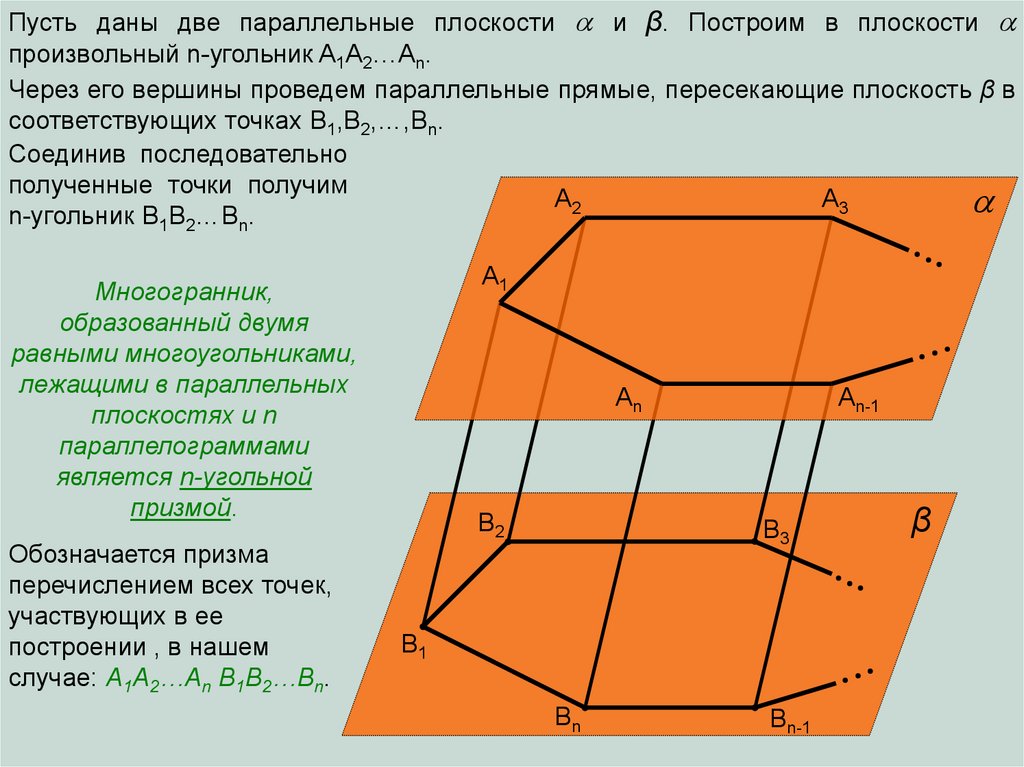
Пусть даны две параллельные плоскости и β. Построим в плоскостипроизвольный n-угольник A1A2…An.
Через его вершины проведем параллельные прямые, пересекающие плоскость β в
соответствующих точках В1,В2,…,Вn.
Соединив последовательно
полученные точки получим
A2
A3
n-угольник B1B2…Bn.
A1
Многогранник,
образованный двумя
равными многоугольниками,
лежащими в параллельных
плоскостях и n
параллелограммами
является n-угольной
призмой.
Обозначается призма
перечислением всех точек,
участвующих в ее
построении , в нашем
случае: A1A2…An B1B2…Bn.
An
B2
An-1
B3
B1
Bn
Bn-1
β
3.
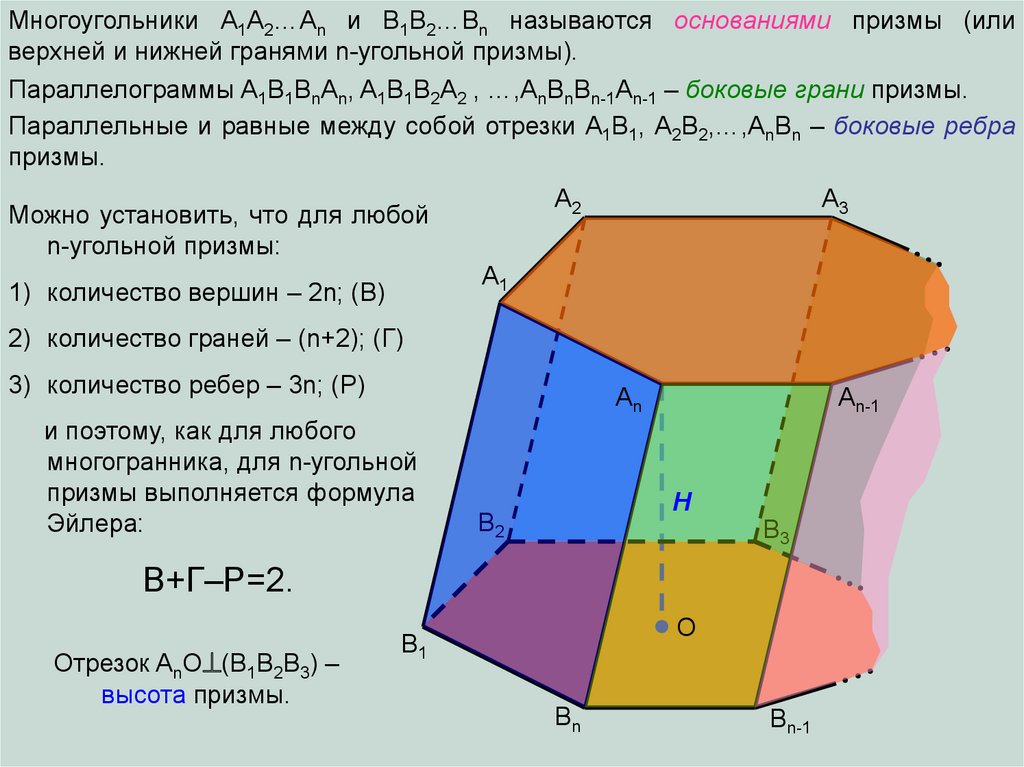
Многоугольники A1A2…An и В1В2…Вn называются основаниями призмы (иливерхней и нижней гранями n-угольной призмы).
Параллелограммы A1B1BnAn, A1B1B2A2 , …,AnBnBn-1An-1 – боковые грани призмы.
Параллельные и равные между собой отрезки A1B1, A2B2,…,AnBn – боковые ребра
призмы.
A2
Можно установить, что для любой
n-угольной призмы:
A3
A1
1) количество вершин – 2n; (В)
2) количество граней – (n+2); (Г)
3) количество ребер – 3n; (Р)
An
и поэтому, как для любого
многогранника, для n-угольной
призмы выполняется формула
Эйлера:
An-1
H
B2
B3
В+Г–Р=2.
Отрезок AnO (B1B2B3) –
высота призмы.
O
B1
Bn
Bn-1
4.
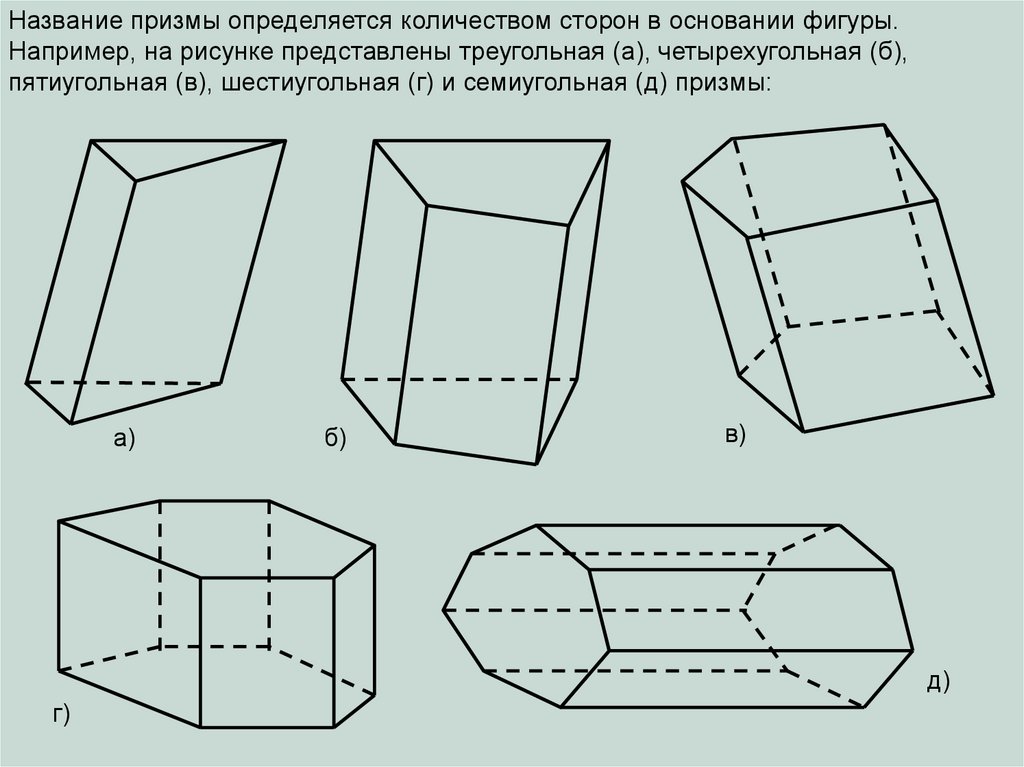
Название призмы определяется количеством сторон в основании фигуры.Например, на рисунке представлены треугольная (а), четырехугольная (б),
пятиугольная (в), шестиугольная (г) и семиугольная (д) призмы:
а)
б)
в)
д)
г)
5.
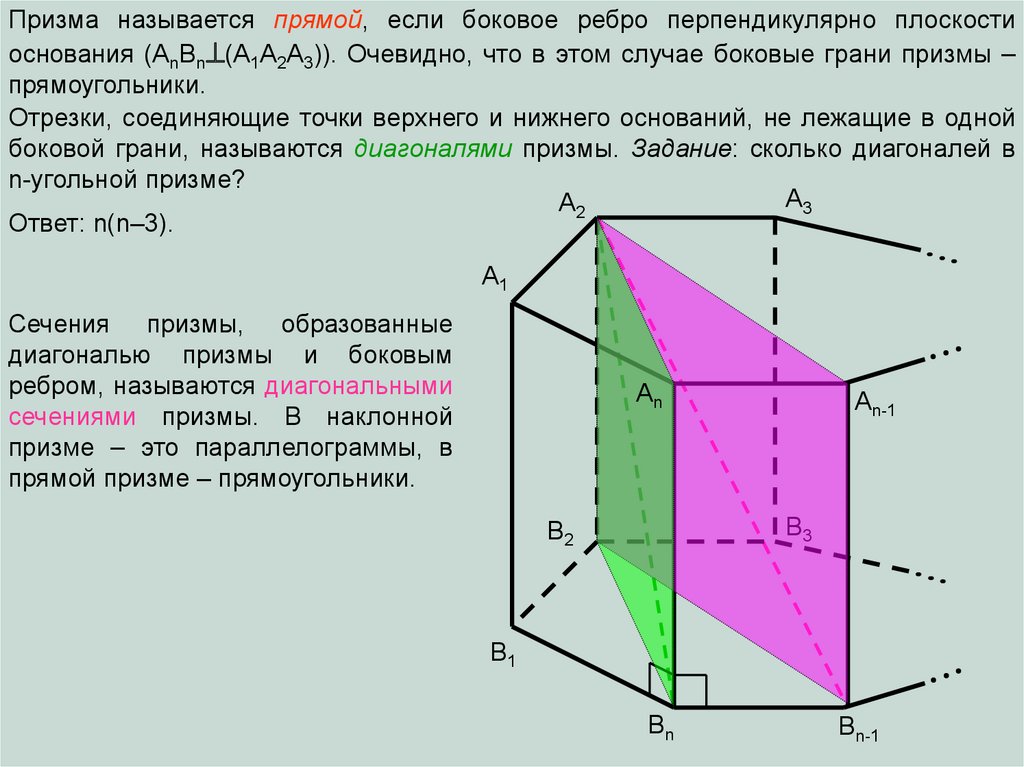
Призма называется прямой, если боковое ребро перпендикулярно плоскостиоснования (AnBn (A1A2A3)). Очевидно, что в этом случае боковые грани призмы –
прямоугольники.
Отрезки, соединяющие точки верхнего и нижнего оснований, не лежащие в одной
боковой грани, называются диагоналями призмы. Задание: сколько диагоналей в
n-угольной призме?
A3
A2
Ответ: n(n–3).
A1
Сечения призмы, образованные
диагональю призмы и боковым
ребром, называются диагональными
сечениями призмы. В наклонной
призме – это параллелограммы, в
прямой призме – прямоугольники.
An
An-1
B3
B2
B1
Bn
Bn-1
6.
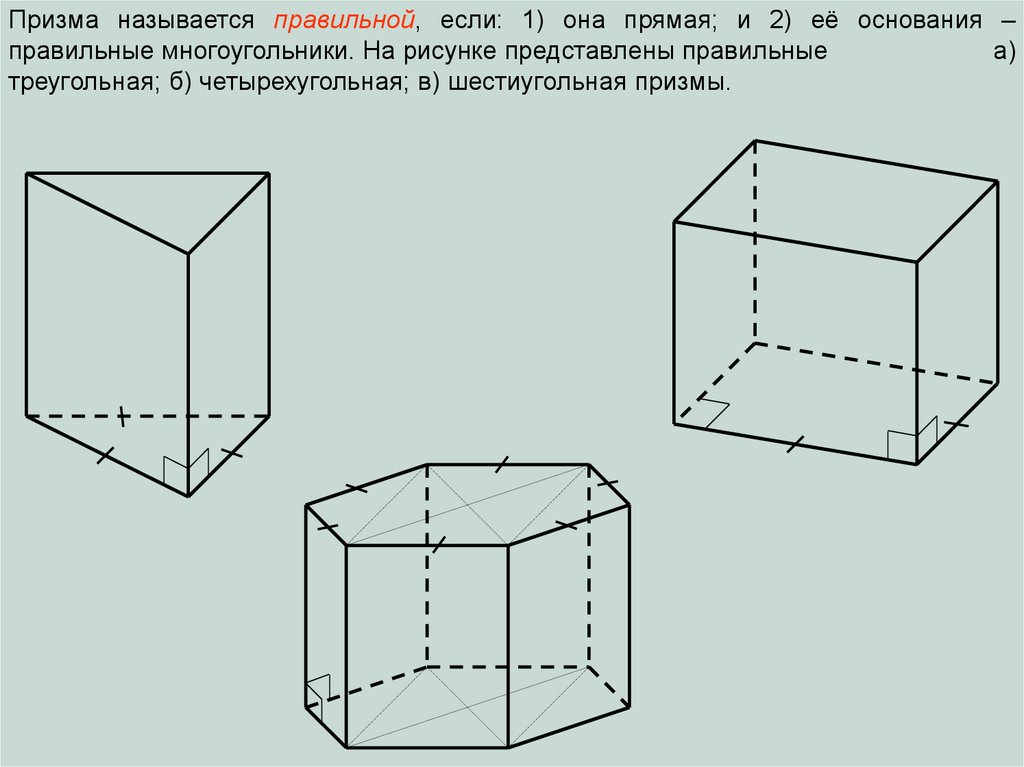
Призма называется правильной, если: 1) она прямая; и 2) её основания –правильные многоугольники. На рисунке представлены правильные
а)
треугольная; б) четырехугольная; в) шестиугольная призмы.
7.
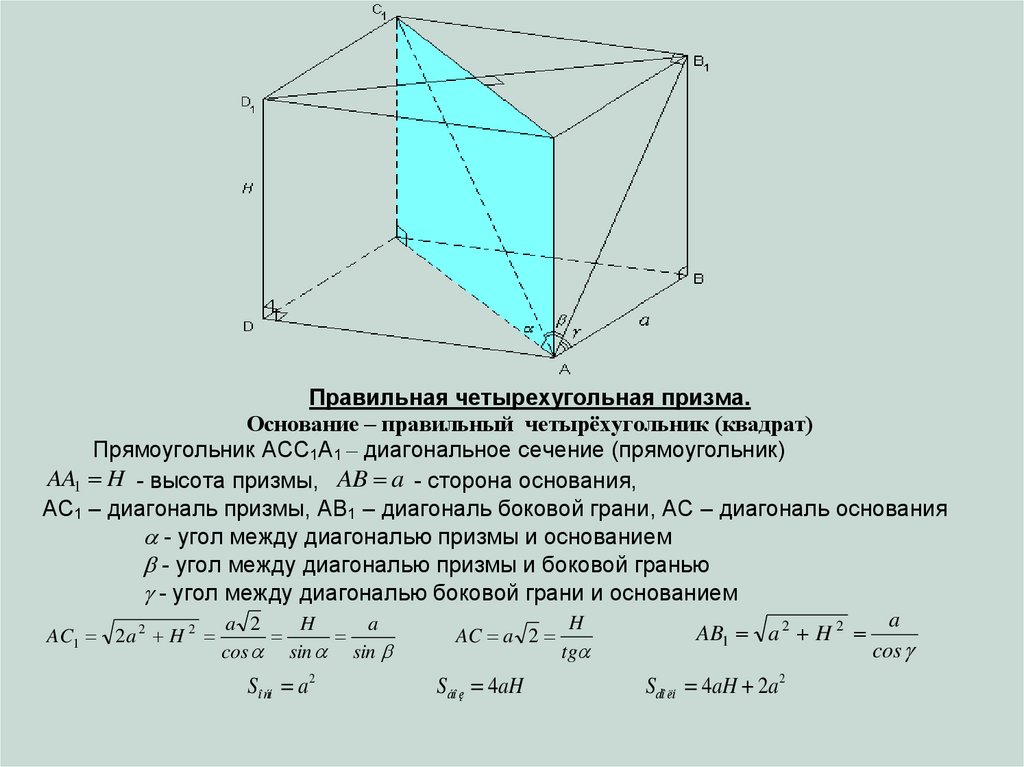
Правильная четырехугольная призма.Основание – правильный четырёхугольник (квадрат)
Прямоугольник ACC1A1 – диагональное сечение (прямоугольник)
AA1 H - высота призмы, AB a - сторона основания,
AC1 – диагональ призмы, AB1 – диагональ боковой грани, AC – диагональ основания
- угол между диагональю призмы и основанием
- угол между диагональю призмы и боковой гранью
- угол между диагональю боковой грани и основанием
a
H
a 2
H
a
AB1 a 2 H 2
AC a 2
AC1 2a 2 H 2
cos
tg
cos sin sin
Sî ńí a 2
Sáî ę 4aH
Sďî ëí 4aH 2a 2
8.
Правильная треугольная призма.Основание – правильный (равносторонний) треугольник
Прямоугольник MCC1M1 – медианное сечение
AA1 H - высота призмы, AB a - сторона основания,
CM - высота основания A 60 0 ACM BCM 30 0
S осн
S бок 3aH
a2 3
4
S полн 3aH
CM
a2 3
2
a 3
2
V S осн H
9.
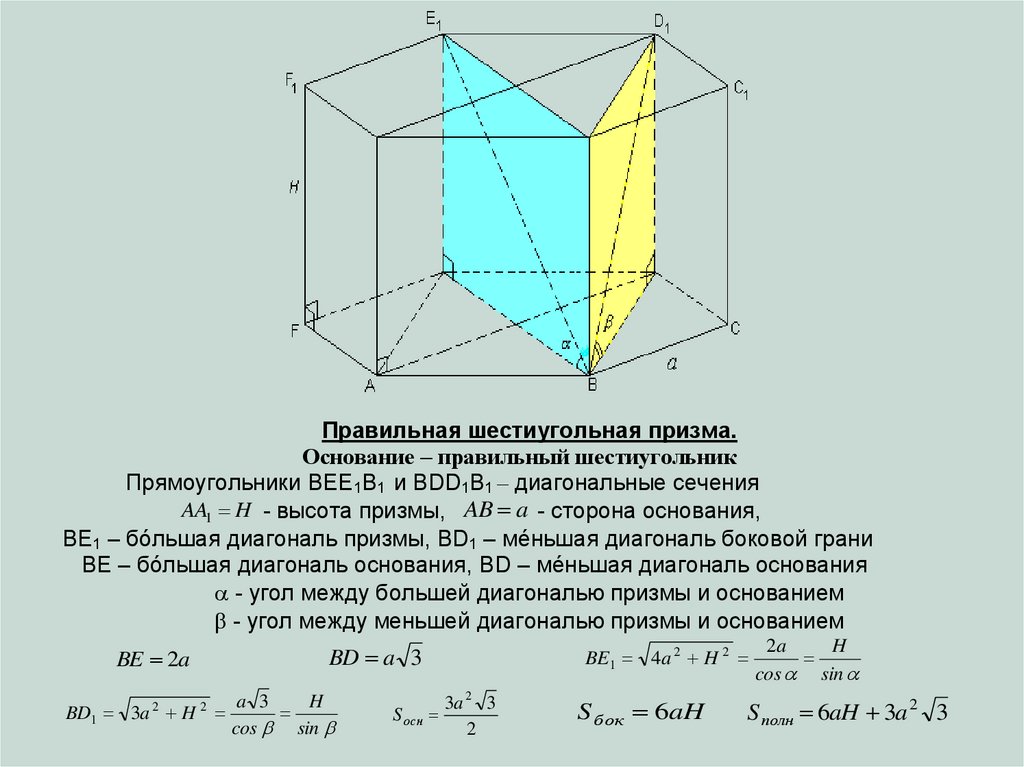
Правильная шестиугольная призма.Основание – правильный шестиугольник
Прямоугольники BEE1B1 и BDD1B1 – диагональные сечения
AA1 H - высота призмы, AB a - сторона основания,
BE1 – бóльшая диагональ призмы, BD1 – мéньшая диагональ боковой грани
BE – бóльшая диагональ основания, BD – мéньшая диагональ основания
- угол между большей диагональю призмы и основанием
- угол между меньшей диагональю призмы и основанием
BD a 3
BE 2a
BD1 3a H
2
2
a 3
H
cos sin
S осн
BE1 4a 2 H 2
3a 2 3
2
S бок 6aH
2a
H
cos sin
S полн 6aH 3a 2 3
10.
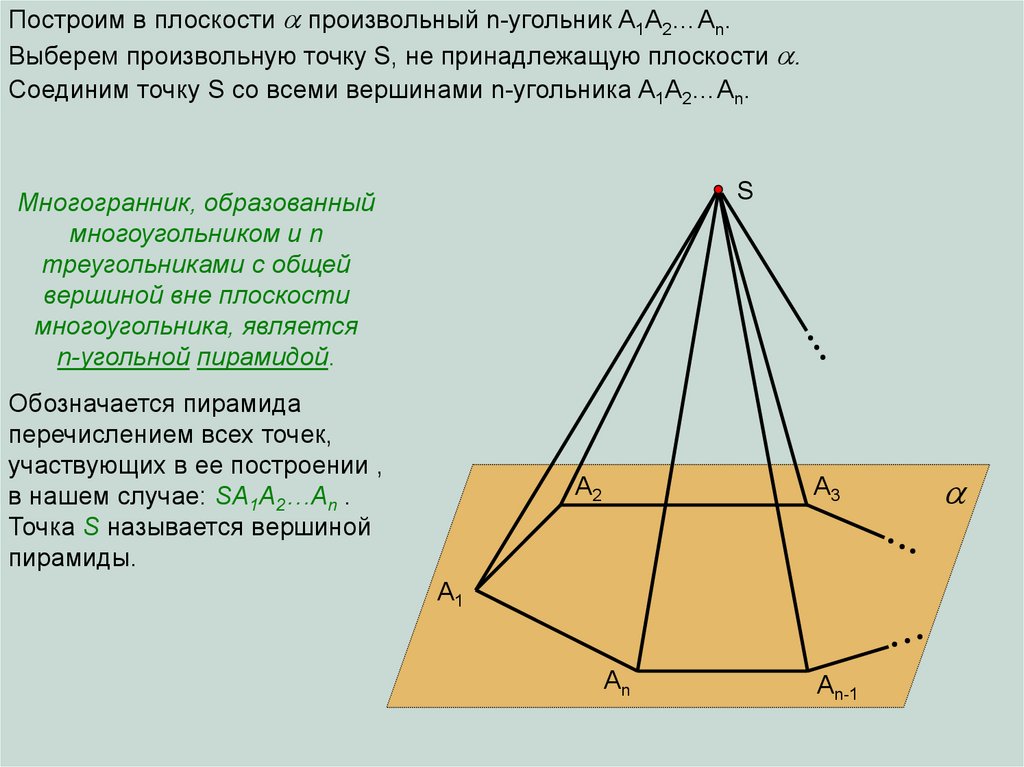
Построим в плоскости произвольный n-угольник A1A2…An.Выберем произвольную точку S, не принадлежащую плоскости .
Соединим точку S со всеми вершинами n-угольника A1A2…An.
S
Многогранник, образованный
многоугольником и n
треугольниками с общей
вершиной вне плоскости
многоугольника, является
n-угольной пирамидой.
Обозначается пирамида
перечислением всех точек,
участвующих в ее построении ,
в нашем случае: SA1A2…An .
Точка S называется вершиной
пирамиды.
A2
A3
A1
An
An-1
11.
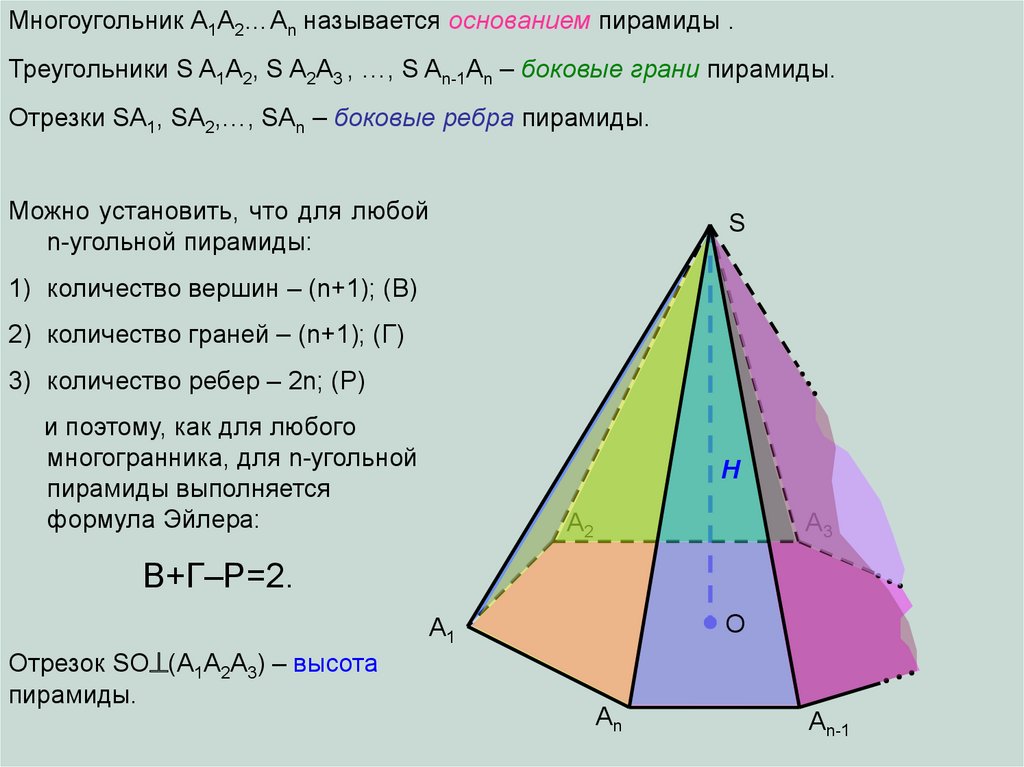
Многоугольник A1A2…An называется основанием пирамиды .Треугольники S A1A2, S A2A3 , …, S An-1An – боковые грани пирамиды.
Отрезки SA1, SA2,…, SAn – боковые ребра пирамиды.
Можно установить, что для любой
n-угольной пирамиды:
S
1) количество вершин – (n+1); (В)
2) количество граней – (n+1); (Г)
3) количество ребер – 2n; (Р)
и поэтому, как для любого
многогранника, для n-угольной
пирамиды выполняется
формула Эйлера:
H
A2
A3
В+Г–Р=2.
Отрезок SO (A1A2A3) – высота
пирамиды.
O
A1
An
An-1
12.
SH
l
A
R
a
2
M
r
O
a
2
C
N
B
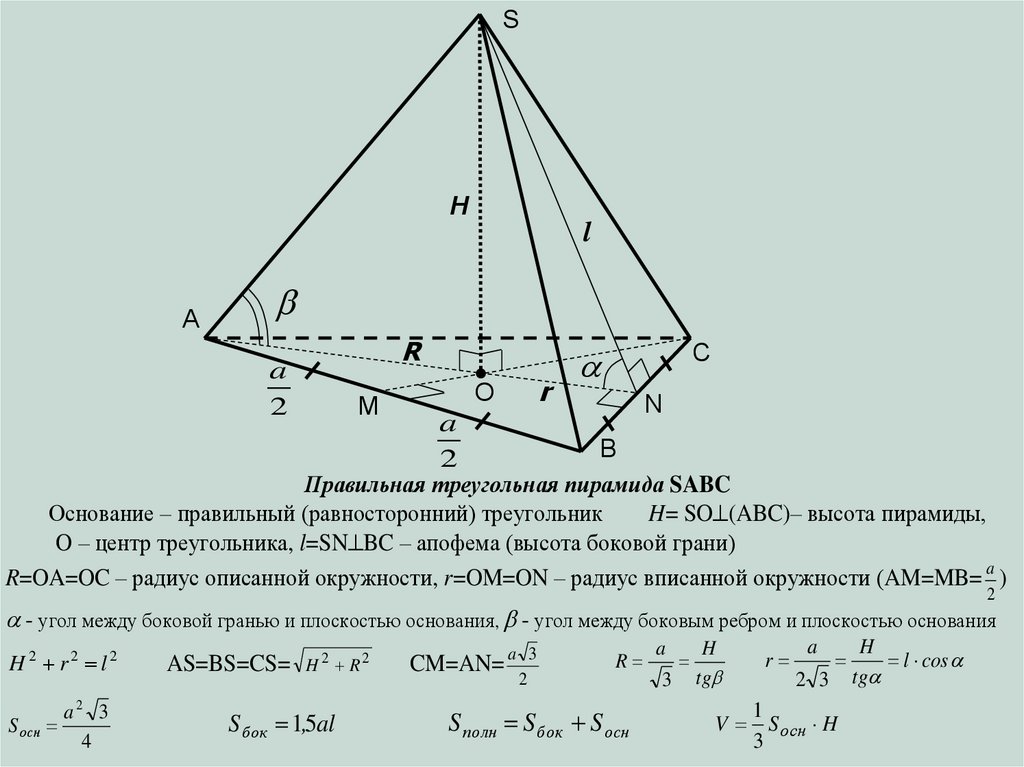
Правильная треугольная пирамида SABC
Основание – правильный (равносторонний) треугольник
H= SO (ABC)– высота пирамиды,
O – центр треугольника, l=SN BC – апофема (высота боковой грани)
R=OA=OC – радиус описанной окружности, r=OM=ON – радиус вписанной окружности (AM=MB= a )
2
- угол между боковой гранью и плоскостью основания, - угол между боковым ребром и плоскостью основания
H 2 r2 l2
S осн
a2 3
4
AS=BS=CS=
H 2 R2
S бок 1,5al
CM=AN= a
3
R
2
S полн S бок S осн
a
3
H
tg
r
a
2 3
1
V S осн H
3
H
l cos
tg
13.
SD
l
H
C
R
O
a
r
M
A
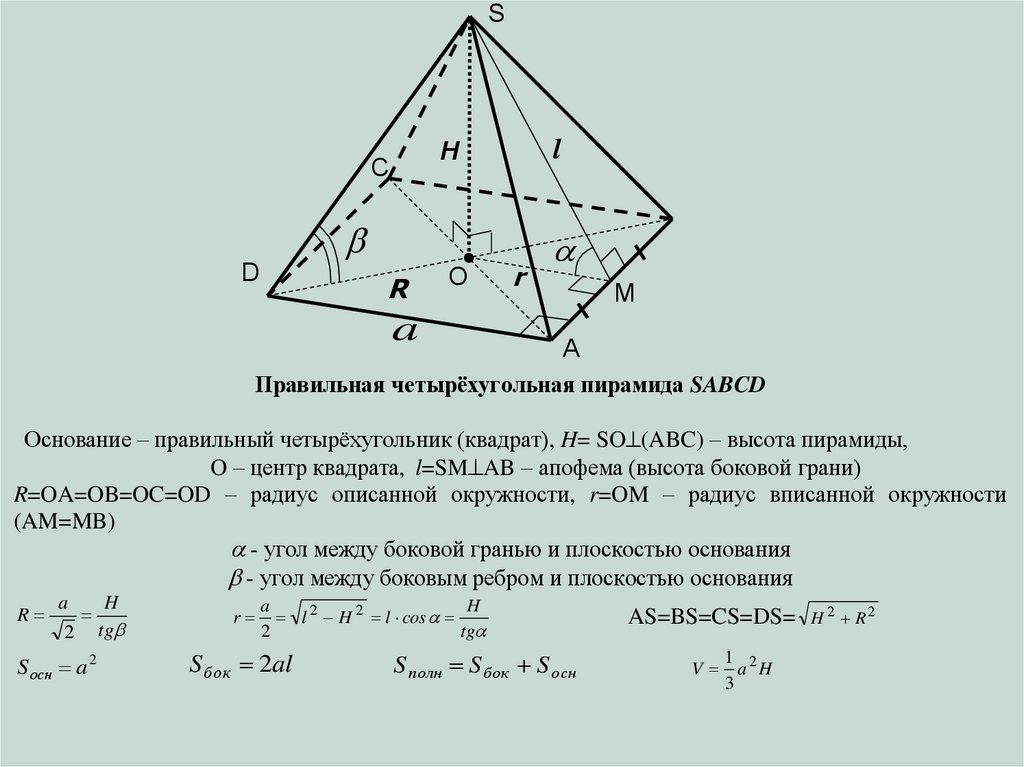
Правильная четырёхугольная пирамида SABCD
Основание – правильный четырёхугольник (квадрат), H= SO (ABC) – высота пирамиды,
O – центр квадрата, l=SM AB – апофема (высота боковой грани)
R=OA=OB=OC=OD – радиус описанной окружности, r=OM – радиус вписанной окружности
(AM=MB)
- угол между боковой гранью и плоскостью основания
- угол между боковым ребром и плоскостью основания
R
a
2
S осн a 2
H
tg
r
a
H
l 2 H 2 l cos
2
tg
S бок 2al
S полн S бок S осн
AS=BS=CS=DS=
1
V a2H
3
H 2 R2
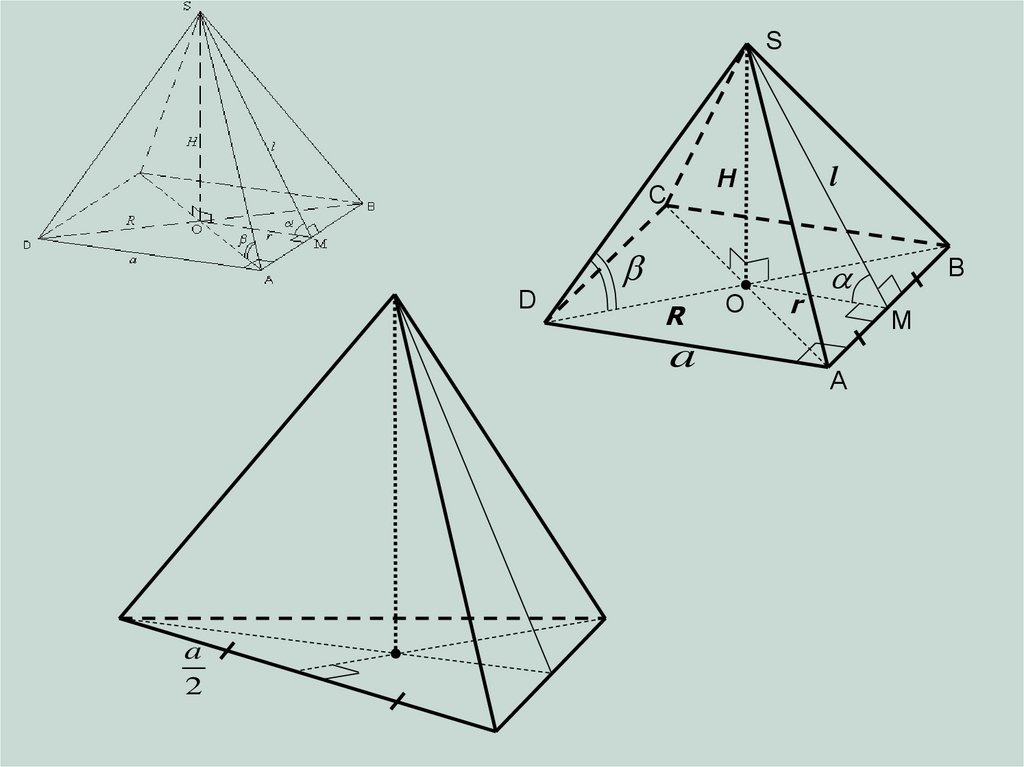
14.
SD
R
a
a
2
l
H
C
O
r
B
M
A


 mathematics
mathematics








