РядыРасп

1. Ряды распределения

2.

Ряд распределения –это упорядоченное
распределение единиц изучаемой совокупности на
группы по определенному варьирующему признаку
Ряд распределения
атрибутивный
вариационный
интервальный
равноинтервальный
дискретный
неравноинтервальный

3. Атрибутивные ряды распределения

это ряды распределения, построенные по
качественным признакам, т. е. признакам, не
имеющим числового выражения.
Они характеризуют состав совокупности по
тем или иным существенным признакам.
Взятые за несколько периодов эти данные
позволяют исследовать изменение
структуры.
Примером атрибутивного ряда
распределения может служить
распределение студентов группы по полу.

4. ряды распределения состоят из двух элементов: вариантов (Х) и частот(f)

• Числовые значения количественного признака в вариационном
ряду распределения называются вариантами. Они могут быть
положительными и отрицательными (прибыль и убыток),
абсолютными и относительными.
• Частоты — это численности отдельных вариантов или каждой
группы вариационного рада, т. е. это числа, показывающие, как
часто встречаются те или иные варианты в ряду распределения.
Сумма всех частот называется объемом совокупности.
• Частости — это частоты, выраженные в виде относительных
величин (долях единиц или процентах). Сумма частостей равна
единице или 100%. Замена частот частостями позволяет
сопоставлять вариационные рады с разным числом наблюдений.
• Вариационные ряды в зависимости от характера вариации
подразделяются на дискретные и интервальные. Дискретные
вариационные ряды основаны на дискретных (прерывных)
признаках, имеющих только целые значения (например,
тарифный разряд рабочих, число детей в семье); интервальные
— на непрерывных признаках (имеющих любые значения, в том
числе и дробные).

5. Интервальный вариационный ряд распределения с равными интервалами

• Величина интервала
(округляется до
точности данных наблюдения)
h
R
k
где R=xmax xmin размах вариации (разность
между максимальным и минимальным значениями
признака);
K – число групп, на которые нужно разбить
совокупность.
k= 1+3.322* lg N ,
где
N – численность единиц
в совокупности.

6. Формирование групп

• Х min+ h (от ** до ***) – 1 группа
• Верхняя граница + h (от ** до ***) – 2
группа
• и т.д.

7.

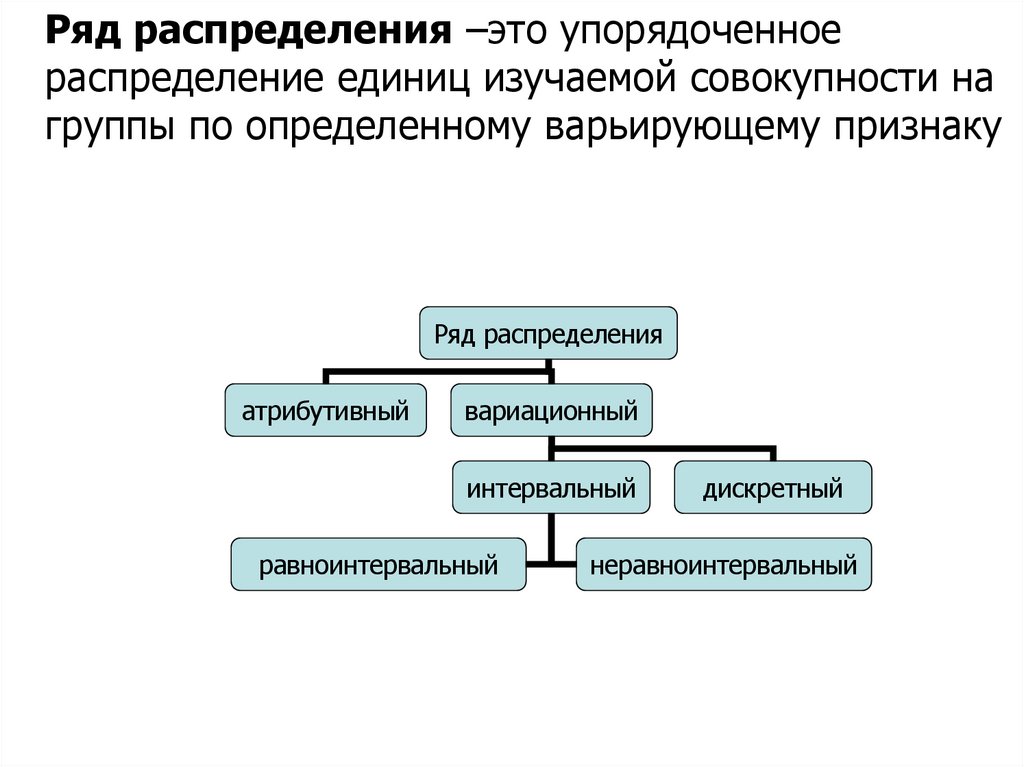
ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЯ
ИНТЕРВАЛЬНЫХ ВАРИАЦИОННЫХ
РЯДОВ РАСПРЕДЕЛЕНИЯ
ГИСТОГРАММА РАСПРЕДЕЛЕНИЯ
f
12
10
8
6
4
2
0
Мо
3
6
9
12
15
х

8.

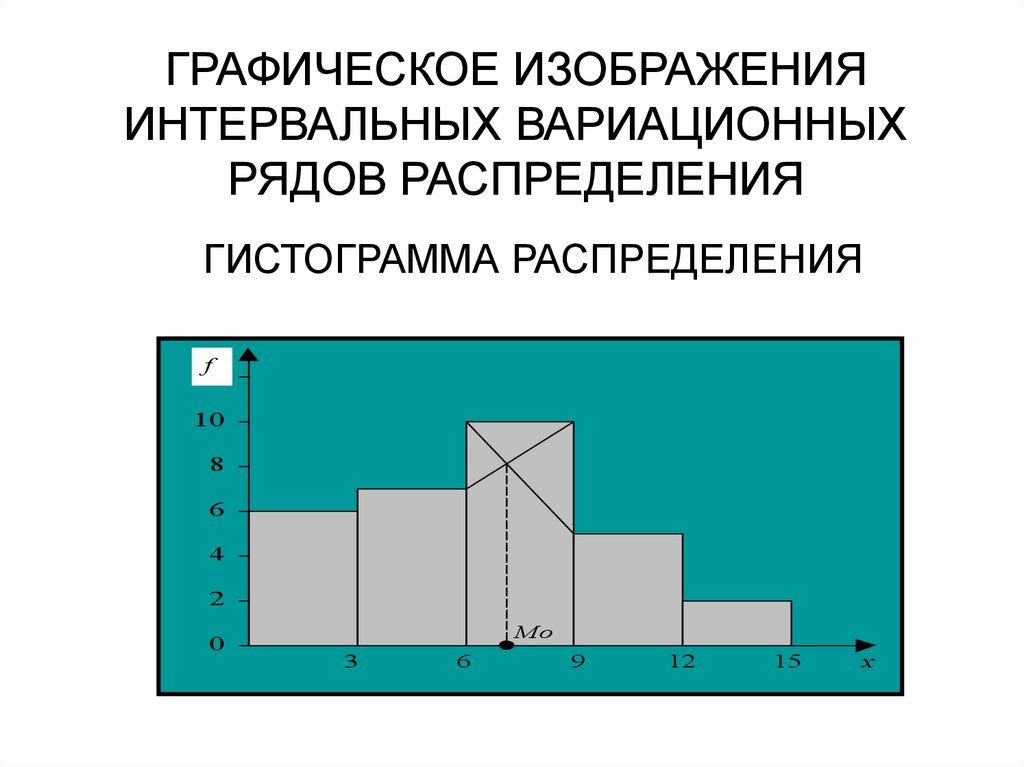
ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЯ
ДИСКРЕТНЫХ ВАРИАЦИОННЫХ РЯДОВ
РАСПРЕДЕЛЕНИЯ
ПОЛИГОН РАСПРЕДЕЛЕНИЯ
f
12
10
8
6
4
2
Mo
0
1,5
4,5
7,5
10,5
13,5
х

9.

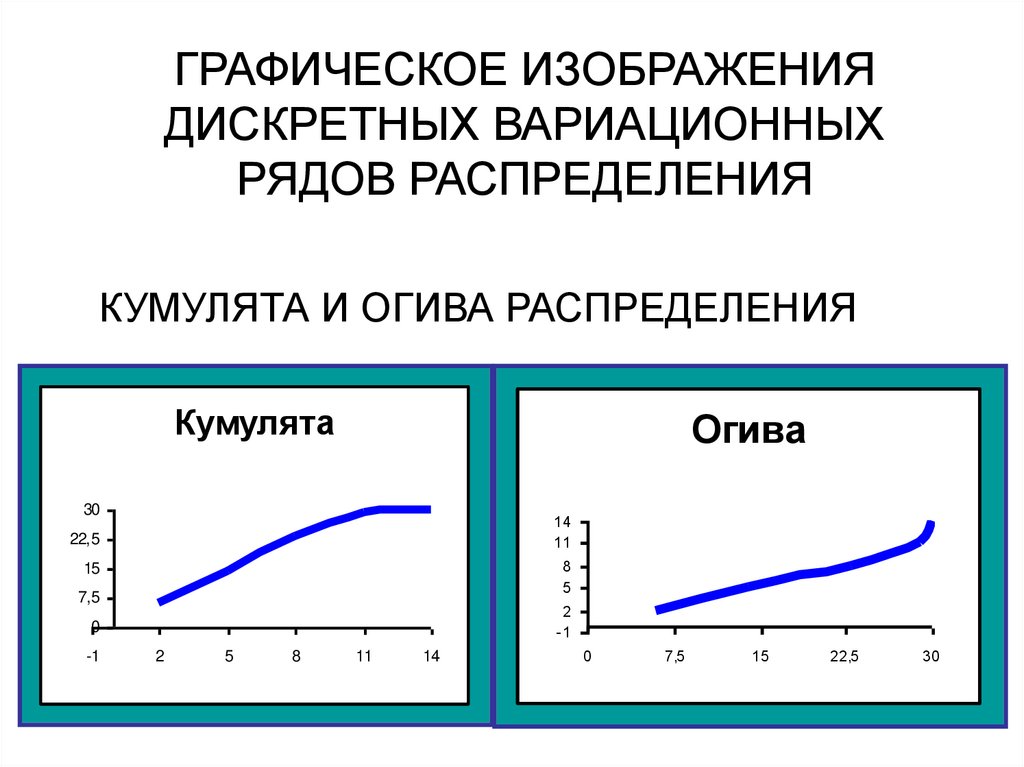
ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЯ
ДИСКРЕТНЫХ ВАРИАЦИОННЫХ
РЯДОВ РАСПРЕДЕЛЕНИЯ
КУМУЛЯТА И ОГИВА РАСПРЕДЕЛЕНИЯ
Кумулята
Огива
30
14
11
22,5
8
5
15
7,5
2
-1
0
-1
2
5
8
11
14
0
7,5
15
22,5
30

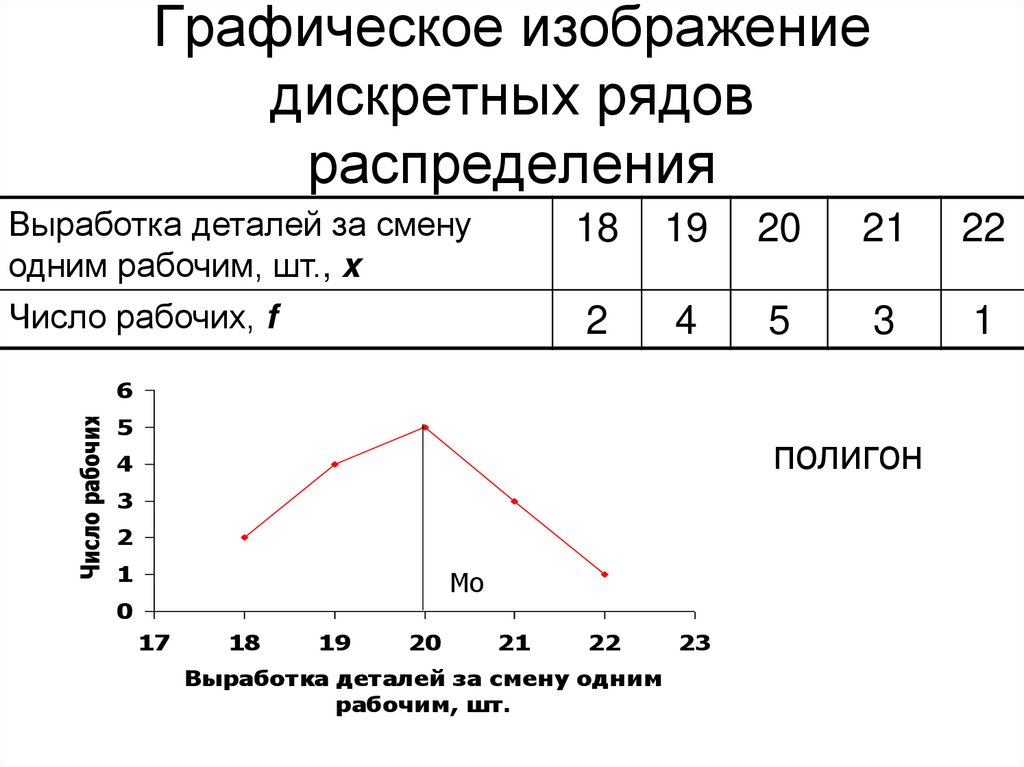
10. Графическое изображение дискретных рядов распределения

Выработка деталей за смену
одним рабочим, шт., x
Число рабочих, f
18
19
20
21
22
2
4
5
3
1
Число рабочих
6
5
полигон
4
3
2
1
Мо
0
17
18
19
20
21
22
Выработка деталей за смену одним
рабочим, шт.
23

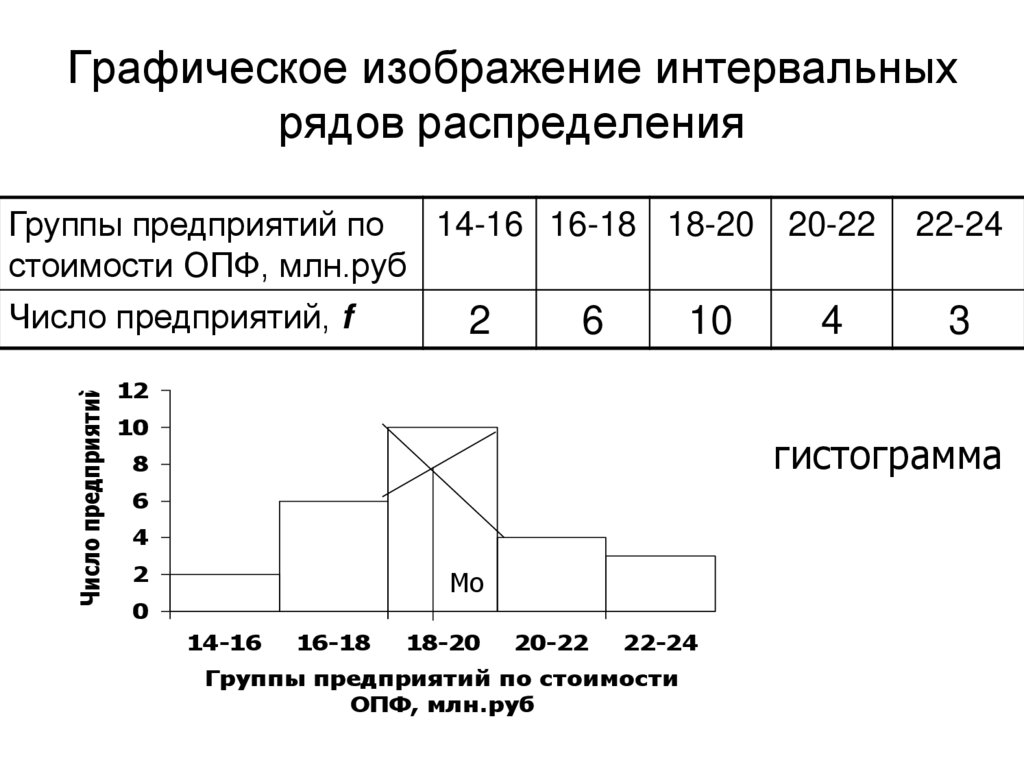
11. Графическое изображение интервальных рядов распределения

Число предприятий
Группы предприятий по
14-16 16-18 18-20 20-22
стоимости ОПФ, млн.руб
Число предприятий, f
2
6
10
4
22-24
3
12
10
гистограмма
8
6
4
2
Мо
0
14-16
16-18
18-20
20-22
22-24
Группы предприятий по стоимости
ОПФ, млн.руб

12. СТРУКТУРНЫЕ СРЕДНИЕ

• Мода (Мо)– это значение признака,
повторяющееся в совокупности с наибольшей
частотой, т.е. отражает наиболее часто
распространенный вариант значения признака.
Поэтому графически мода изображается на
полигоне или гистограмме.
• Медиана (Ме)– это значение признака,
приходящееся на середину ранжированной
совокупности. Поэтому графически медиана
изображается на кумуляте или огиве. Для
определения медианного значения признака
находят номер медианной единицы ряда, n 1
N Me
используя формулу:
2
где n – объем совокупности.

13. МОДА

M o x M o hM o
f M o f M o 1
( f M o f M o 1 ) ( f M o f M o 1 )
где хмо – нижняя граница модального интервала,
hМо –величина модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, предшествующего
модальному,
fМо+1 – частота интервала, следующего за
модальным.

14. МЕДИАНА

M е x M е hM е
1
2
f
S M e 1
f Mе
где хМе – нижняя граница медианного
интервала,
hМе –величина медианного интервала,
fМе – частота медианного интервала,
SМе-1 – накопленная частота интервала,
предшествующего медианному

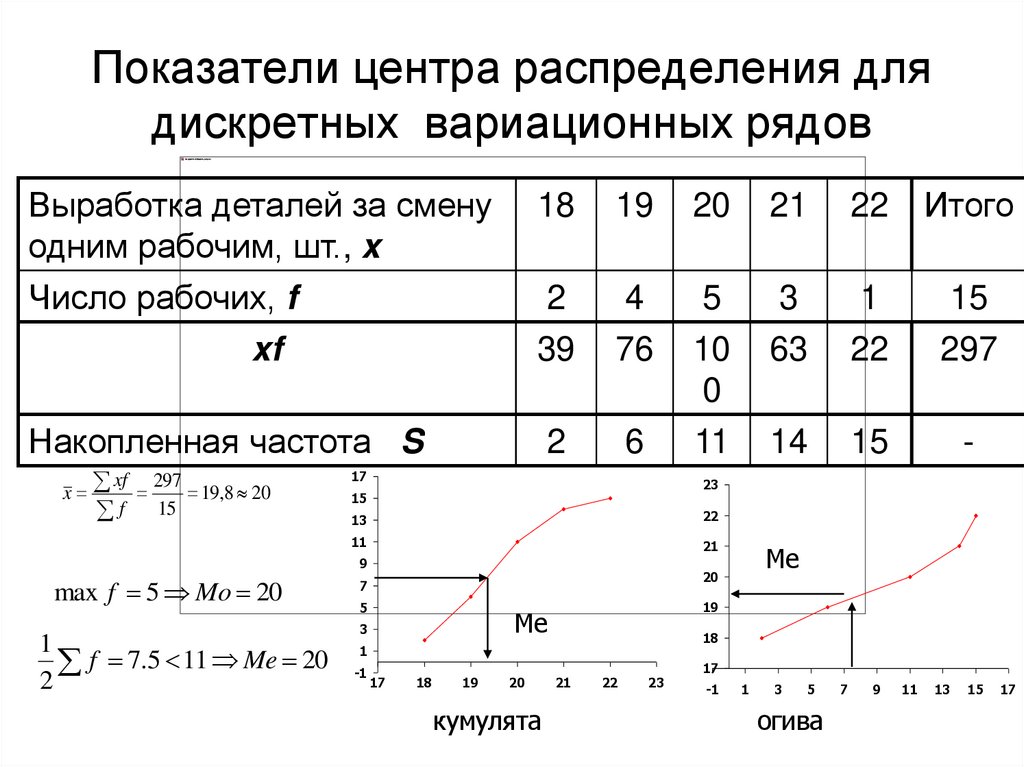
15. Показатели центра распределения для дискретных вариационных рядов

Выработка деталей за смену
одним рабочим, шт., x
Число рабочих, f
xf
18
19
20
21
22
Итого
2
39
4
76
3
63
1
22
15
297
Накопленная частота S
2
6
5
10
0
11
14
15
-
x
xf 297 19,8 20
f 15
17
23
15
13
22
11
21
9
max f 5 Mo 20
1
f 7.5 11 Me 20
2
7
5
19
Me
3
18
1
-1
Me
20
17
18
19
20
кумулята
21
22
23
17
-1
1
3
5
огива
7
9
11
13
15
17

16. Выводы по показателям центра распределения:

• Х: В среднем один рабочий за смену
производит 20 деталей
• Мо: Большинство рабочих за смену
производит 20 деталей
• Ме: Первые 7 рабочих за смену
производят не более 20 деталей, а
последние 7 рабочих за смену
производят не менее 20 деталей.

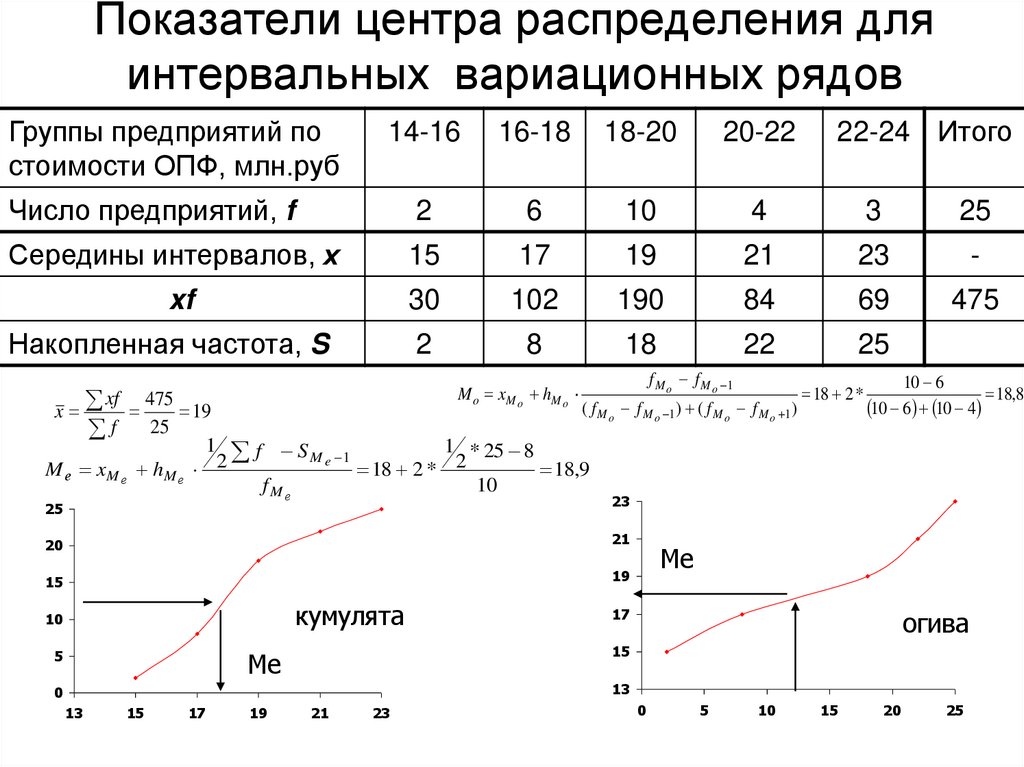
17. Показатели центра распределения для интервальных вариационных рядов

Группы предприятий по
стоимости ОПФ, млн.руб
22-24 Итого
14-16
16-18
18-20
20-22
Число предприятий, f
2
6
10
4
3
25
Середины интервалов, х
15
17
19
21
23
-
xf
30
102
190
84
69
475
Накопленная частота, S
2
8
18
22
25
M o xM o hM o
xf 475 19
x
f 25
f M o f M o 1
( f M o f M o 1 ) ( f M o f M o 1 )
1 f S M 1
1 * 25 8
e
2
M е xM е hM е
18 2 * 2
18,9
fM е
10
23
20
21
15
19
25
кумулята
10
5
18 2 *
10 6
18,8
10 6 10 4
Me
17
огива
15
Me
13
0
13
15
17
19
21
23
0
5
10
15
20
25

18. Выводы по показателям центра распределения:

• Х: В среднем основные фонды на предприятии
стоят 19 млн.руб.
• Мо: На большинстве предприятий основные
фонды стоят 18,8 млн.руб.
• Ме: На первых 12 предприятиях основные
фонды стоят не более 18,9 млн.руб., а на
последних 12 предприятиях основные фонды
стоят не менее 18,9 млн.руб.. 13-ое предприятие
имеет основные фонды на сумму 18,9 млн.руб.

19. Показатели вариации

• Вариация – это различие
(колеблемость) значений
анализируемого признака в
один и тот же момент времени.

20. Показатели вариации

Абсолютные:
• Размах вариации
Относительные:
• Коэффициент осцилляции
R xmax xmin
KR
• Среднее линейное
отклонение
d
x x
d
n
x x f
f
R
*100%
x
• Относительное линейное
отклонение
d
Kd
x
*100%
• Коэффициент вариации
KV
• Дисперсия
D
x x х х
x
*100%
2
2
2
2
n
x x f х х
D
f
2
2
2
• Среднеквадратичное
отклонение
D
2
колеблемость :
Слабая
<10%
Умеренная
10-25
Сильная
>25
Однородность совокупности -33%
• Коэффициент асимметрии
As
x Mo
*100%

21. Алгоритм расчета среднеквадратического отклонения:

–находим среднюю арифметическую ряда (х );
–находим отклонение каждой варианты от средней арифметической
( хi х);
–возводим каждое отклонение в квадрат ( хi х)2;
–умножаем каждый квадрат отклонений на соответствующий вес
(
)2хfi i; х
–суммируем все произведения (хi х )2fi;
–делим сумму произведений на сумму частот и получаем дисперсию
x x f
i
f
2
2
;
–извлекаем квадратный корень из частного и получаем
среднеквадратическое отклонение
xi x f
f
2

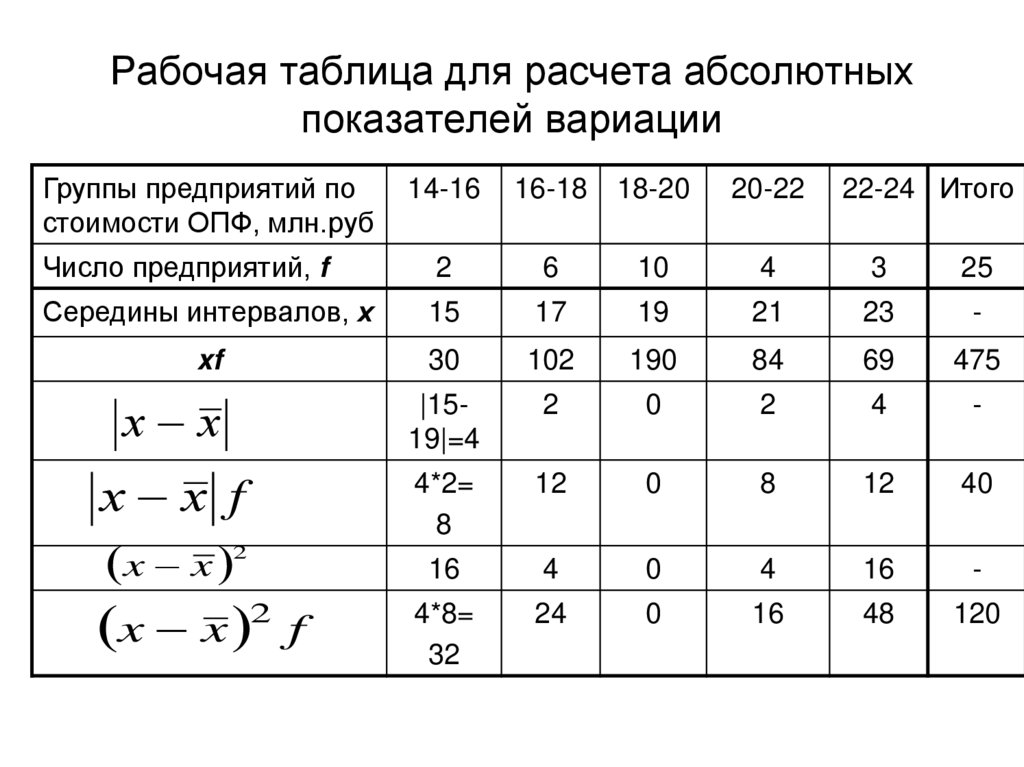
22. Рабочая таблица для расчета абсолютных показателей вариации

Группы предприятий по
стоимости ОПФ, млн.руб
22-24 Итого
14-16
16-18
18-20
20-22
Число предприятий, f
2
6
10
4
3
25
Середины интервалов, х
15
17
19
21
23
-
xf
30
102
190
84
69
475
х х
|1519|=4
2
0
2
4
-
х х f
x x 2
4*2=
8
12
0
8
12
40
16
4
0
4
16
-
x x 2 f
4*8=
32
24
0
16
48
120

23. Показатели вариации

Абсолютные:
• Размах вариации
R xmax xmin 24 14 10
• Среднее линейное
отклонение
x x f 40
d
1,6
f
25
Относительные:
• Коэффициент осцилляции
KR
R
10
* 100% * 100% 53%
x
19
• Относительное линейное
отклонение
Kd
d
1,6
* 100%
* 100% 8,4%
x
19
2,19
* 100% 11,5%
19
• Дисперсия
x x 2 f 2 2 120
D
х х
4,8 • Коэффициент вариации
25
f
• Среднеквадратичное
отклонение
D 4,8 2,19
KV
x
* 100%

24. Выводы по показателям вариации:

• R: стоимость основных фондов колеблется в
пределах от 14 до 24 млн.руб.
• КR: крайние значения составляют от средней
стоимости основных фондов 53%
• d: средневзвешенное отклонение от средней
стоимости основных фондов в ту и другую сторону
составляет 1.6 млн.руб.
• Kd: средневзвешенное отклонение от средней
стоимости основных фондов составляет 8,4% от
средней стоимости основных фондов.

25. Выводы по наиболее важным показателям вариации:

σ=2.19: квадрат отклонений стоимости
основных фондов от средней стоимости
основных фондов в ту и другую сторону
составляет 2,19 млн.руб.
• V=11.5%
1. 10 < 11.5 < 25 Значит изменение стоимости
основных фондов умеренное
2. 11.5 < 33 Значит совокупность однородная

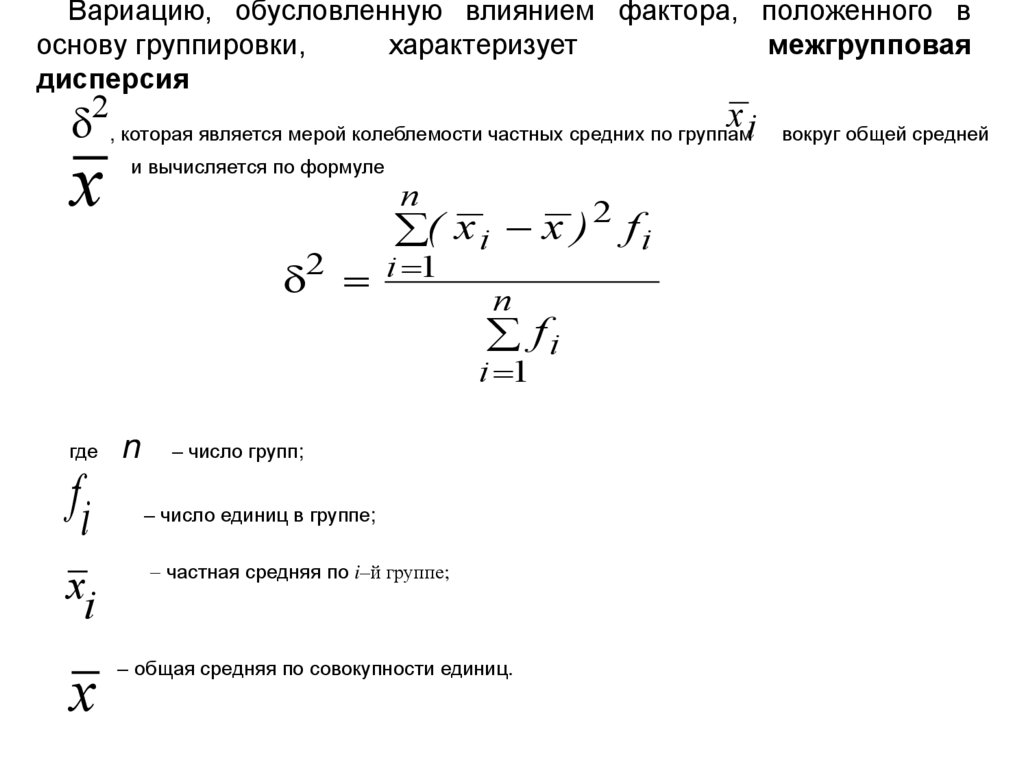
26.

Вариацию, обусловленную влиянием фактора, положенного в
основу группировки,
характеризует
межгрупповая
дисперсия
2
x i вокруг общей средней
, которая является мерой колеблемости частных средних по группам
x
и вычисляется по формуле
n
2
( x i x ) f i
2 i 1
n
fi
i 1
где
fi
xi
x
n
– число групп;
– число единиц в группе;
частная средняя по i–й группе;
– общая средняя по совокупности единиц.

27.

Вариацию, обусловленную влиянием прочих
факторов,
характеризует в каждой группе внутригрупповая
дисперсия 2
i
k
.
( x ij x i )
j 1
2
i
.
k
2

28.

По совокупности в целом вариация значений признака
под влиянием прочих факторов характеризуется
средней из внутригрупповых дисперсий.
k
n
( x ij x i )
j 1 i 1
2
n
или
n
.
2
2
in
i
n
2

29.

Общая дисперсия,
характеризует вариацию признака под
действием всех факторов
n
2
2
( x i x ) f i
i
1
D( x )
n
fi
i 1
,
2
2
x x
2

30. ПРАВИЛО СЛОЖЕНИЯ ДИСПЕРСИЙ

• общая дисперсия равна сумме средней
из внутригрупповых и межгрупповой
дисперсии:
2
2
2
i i

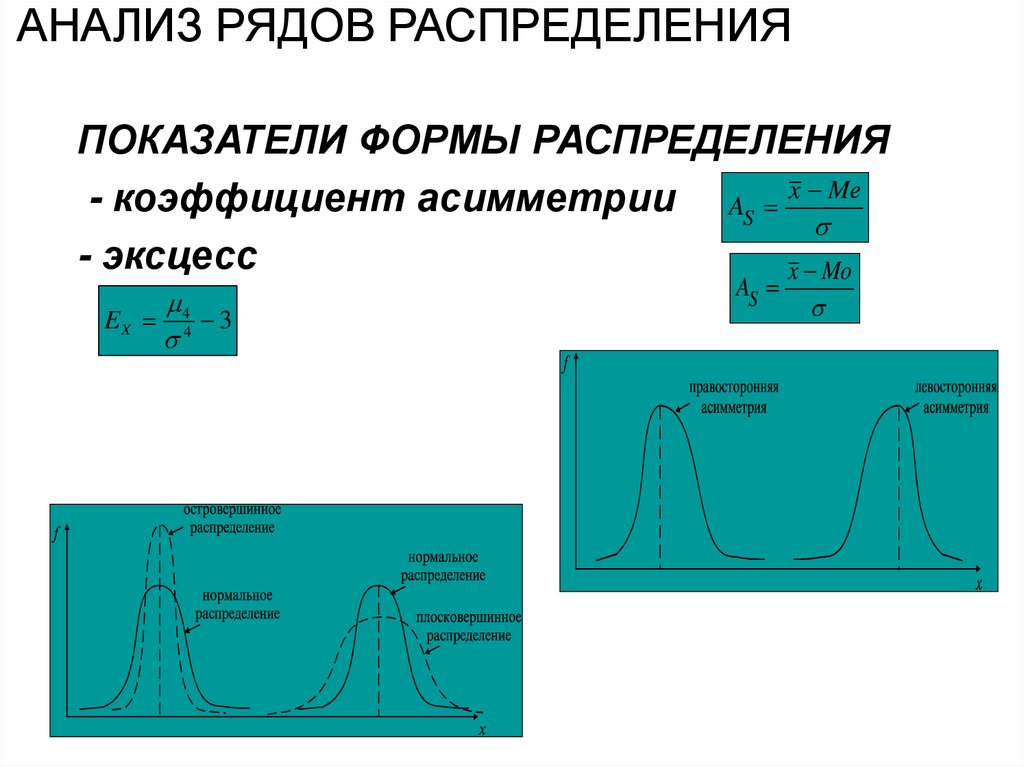
31.

АНАЛИЗ РЯДОВ РАСПРЕДЕЛЕНИЯ
ПОКАЗАТЕЛИ ФОРМЫ РАСПРЕДЕЛЕНИЯ
- коэффициент асимметрии AS x Mе
- эксцесс
x Mo
E X 44 3
AS

32. Коэффициент асимметрии

• Если As >0, то распределение
имеет правостороннюю
асимметрию
• Если As < 0, то распределение
имеет левостороннюю
асимметрию.
• Если As =0, то распределение
симметричное ( х = Мо = Ме).

33. Эксцесс

4
EX
3
4
где
4 центральный момент четвертого порядка
( x x ) 4 f
4= f
Моментом распределения называется средняя
арифметическая отклонений индивидуальных
значений признака от определенной исходной
величины
• Если < 0, то распределение плосковершинное
• Если > 0 , то распределение островершинное
• Если = 0 , то нормальное распределение

34.

Коэффициент асимметрии
Группы предприятий по
стоимости ОПФ, млн.руб
22-24 Итого
14-16
16-18
18-20
20-22
Число предприятий, f
2
6
10
4
3
25
Середины интервалов, х
15
17
19
21
23
-
xf
30
102
190
84
69
475
xf 475 19
x
f 25
M o xM o hM o
As
x Mo
f M o f M o 1
( f M o f M o 1 ) ( f M o f M o 1 )
* 100 %
18 2 *
10 6
18,8
10 6 10 4
19 18,8
* 100 %
2,19
Т.к. As >0, то распределение имеет правостороннюю
асимметрию

35.

АНАЛИЗ РЯДОВ РАСПРЕДЕЛЕНИЯ
ПОКАЗАТЕЛИ РЯДА РАСПРЕДЕЛЕНИЯ
• ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ:
ПОКАЗАТЕЛИ СТРУКТУРЫ РАСПРЕДЕЛЕНИЯ
- СРЕДНЯЯ ВЕЛИЧИНА
• ПОКАЗАТЕЛИ ВАРИАЦИИ
• ПОКАЗАТЕЛИ ФОРМЫ РАСПРЕДЕЛЕНИЯ
-

36. РАВНОМЕРНОСТЬ И РИТМИЧНОСТЬ

37. Анализ сроков и объемов поставки

• Равномерность поставки – это поступление
товара равными партиями через равные
промежутки времени (ρ=1-V).
• Ритмичность поставки – это соблюдение
сроков и объемов поставки, оговоренных
контрактом с учетом сезонных и цикличных
особенностей производства, продажи или
потребления (Каритм).

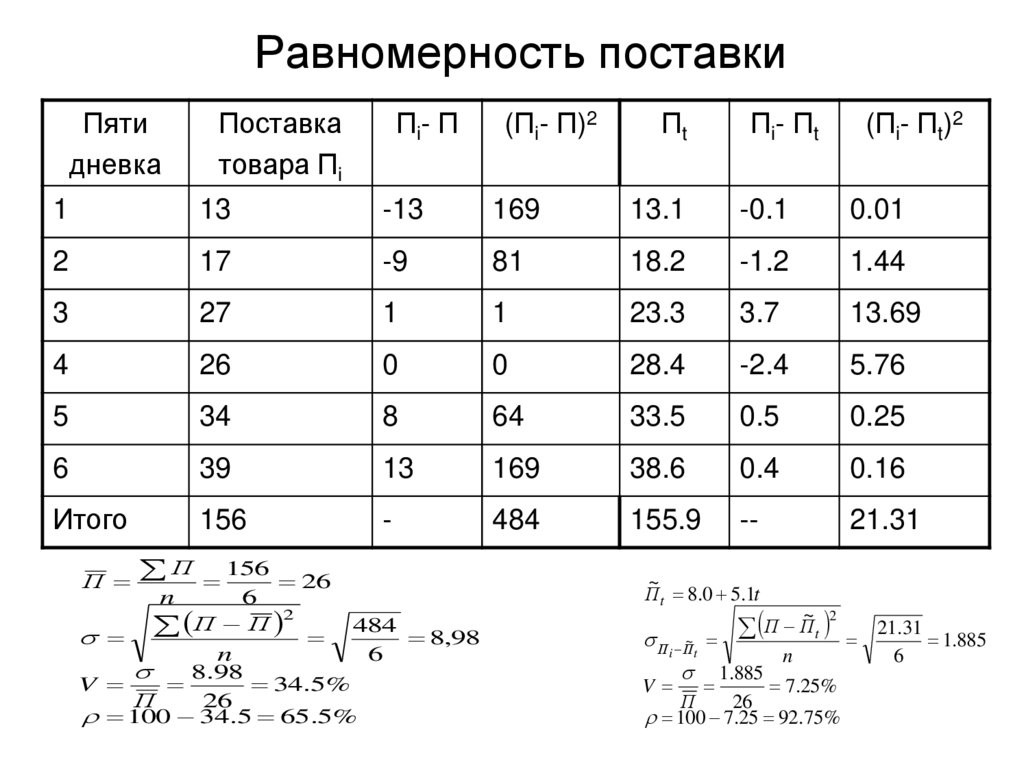
38. Равномерность поставки

Пяти
дневка
Поставка
товара Пi
Пi- П
(Пi- П)2
1
13
-13
169
2
17
-9
3
27
4
Пi- Пt
(Пi- Пt)2
13.1
-0.1
0.01
81
18.2
-1.2
1.44
1
1
23.3
3.7
13.69
26
0
0
28.4
-2.4
5.76
5
34
8
64
33.5
0.5
0.25
6
39
13
169
38.6
0.4
0.16
Итого
156
-
484
155.9
--
21.31
П
П 156 26
n
6
2
П П
484
8,98
n
6
8.98
V
34.5%
П
26
100 34.5 65.5%
Пt
~
П t 8.0 5.1t
П П~
П П t
~
2
n
1.885
V
7.25%
П
26
100 7.25 92.75%
i
t
21.31
1.885
6

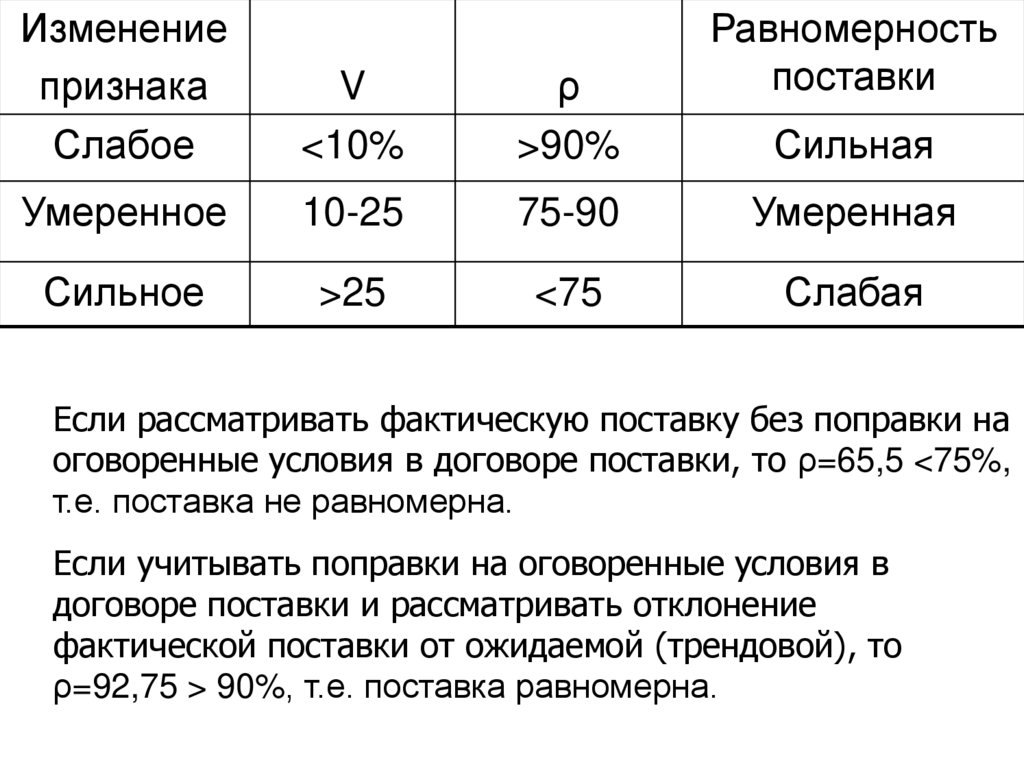
39.

Изменение
признака
Слабое
Равномерность
поставки
V
<10%
ρ
>90%
Умеренное
10-25
75-90
Умеренная
Сильное
>25
<75
Слабая
Сильная
Если рассматривать фактическую поставку без поправки на
оговоренные условия в договоре поставки, то ρ=65,5 <75%,
т.е. поставка не равномерна.
Если учитывать поправки на оговоренные условия в
договоре поставки и рассматривать отклонение
фактической поставки от ожидаемой (трендовой), то
ρ=92,75 > 90%, т.е. поставка равномерна.

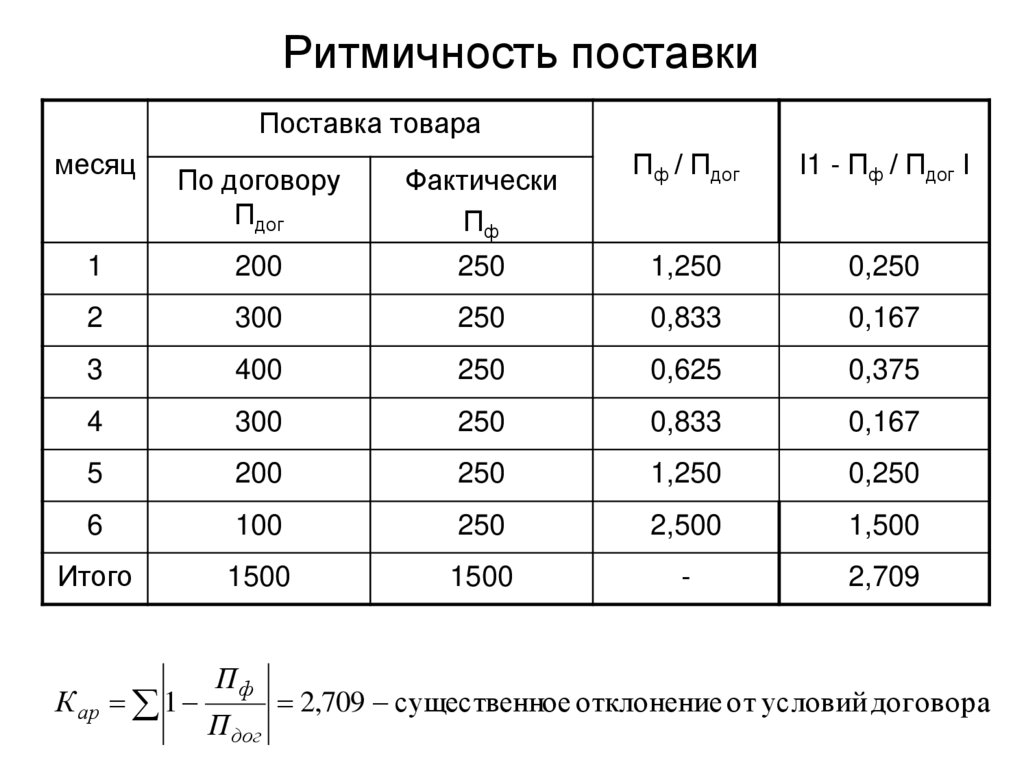
40. Ритмичность поставки

Поставка товара
месяц
Пф / Пдог
І1 - Пф / Пдог І
250
1,250
0,250
300
250
0,833
0,167
3
400
250
0,625
0,375
4
300
250
0,833
0,167
5
200
250
1,250
0,250
6
100
250
2,500
1,500
Итого
1500
1500
-
2,709
По договору
Пдог
Фактически
Пф
1
200
2
К ар 1
Пф
П дог
2,709 существенное отклонение от условий договора