Similar presentations:
Показатели вариации и анализ частотных распределений
1. Показатели вариации и анализ частотных распределений
2.
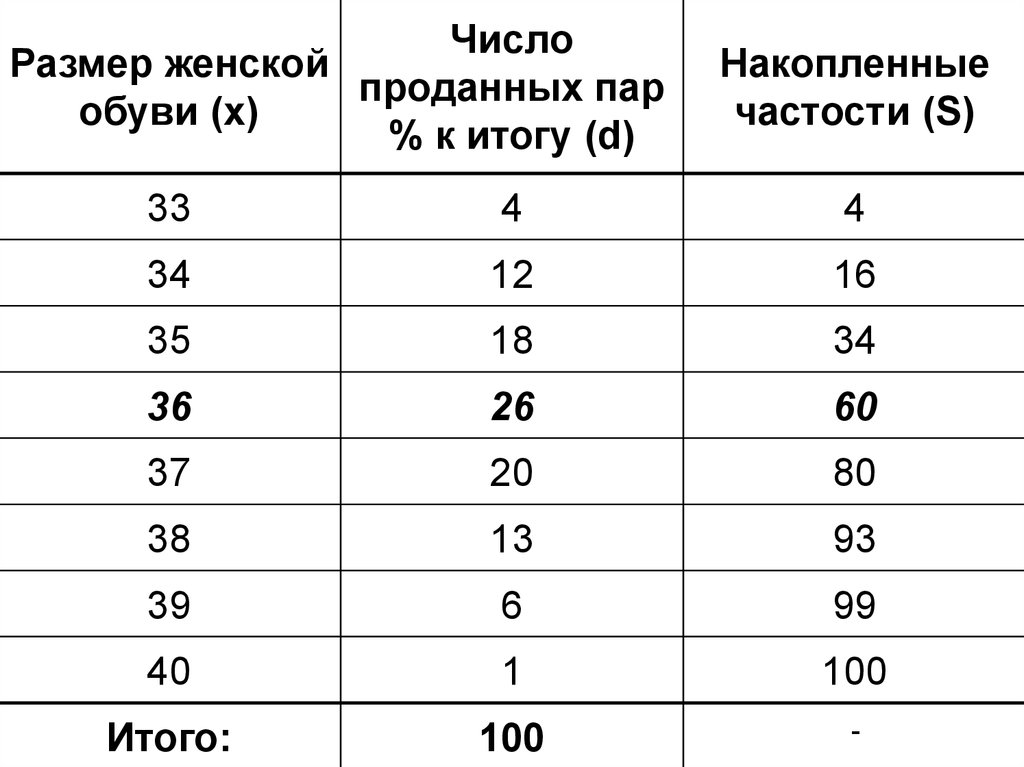
ЧислоРазмер женской
проданных пар
обуви (x)
% к итогу (d)
Накопленные
частости (S)
33
4
4
34
12
16
35
18
34
36
26
60
37
20
80
38
13
93
39
6
99
40
1
100
Итого:
100
-
3.
fMO fMO 1Mo x 0 i
( fMO fMO 1) ( fMO fMO 1)
Где:
x0 и i
FMo
FMo-1
FMo+1
– соответственно нижняя
граница и величина модального
интервала
частоты (частости)
модального, предмодального и
послемодального интервалов
–
4.
НакоплеСередина
нная
интервала
частота
(x’)
(S)
Ставка по
кредиту,
% (х)
Число
банков
(f)
До 14
20
20
13
260
14-16
30
50
15
450
16-18
25
75
17
425
18-20
15
90
19
285
20 и более
10
100
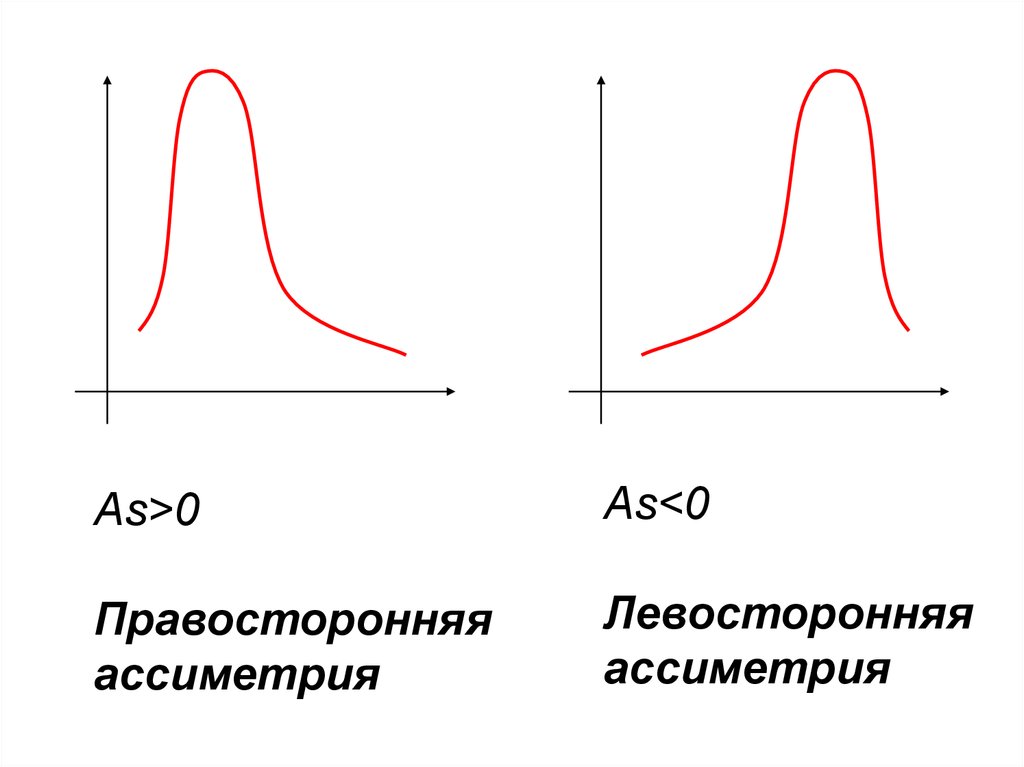
21
210
Итого
100
-
-
1630
x’f
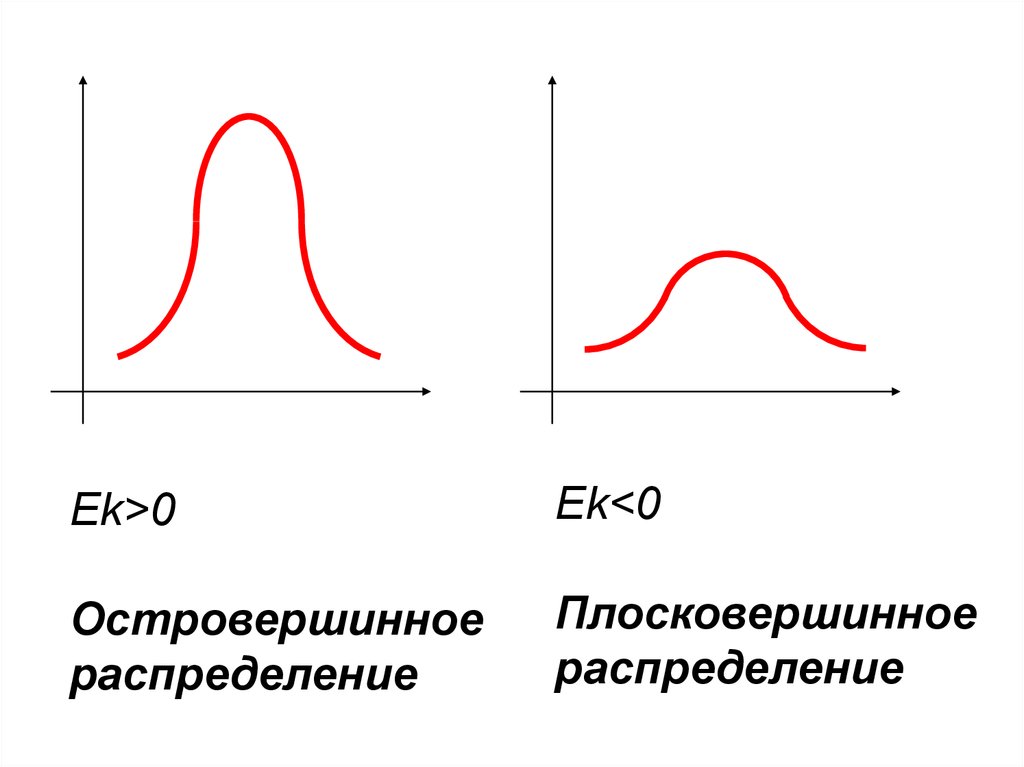
5.
14-16% - модальный интервалШирина интервала
Нижняя граница
Частота
i=2
x0=14
fMo=30
Предмодальная частота
fMo-1=20
Послемодальная частота
fMo+1=25
30 20
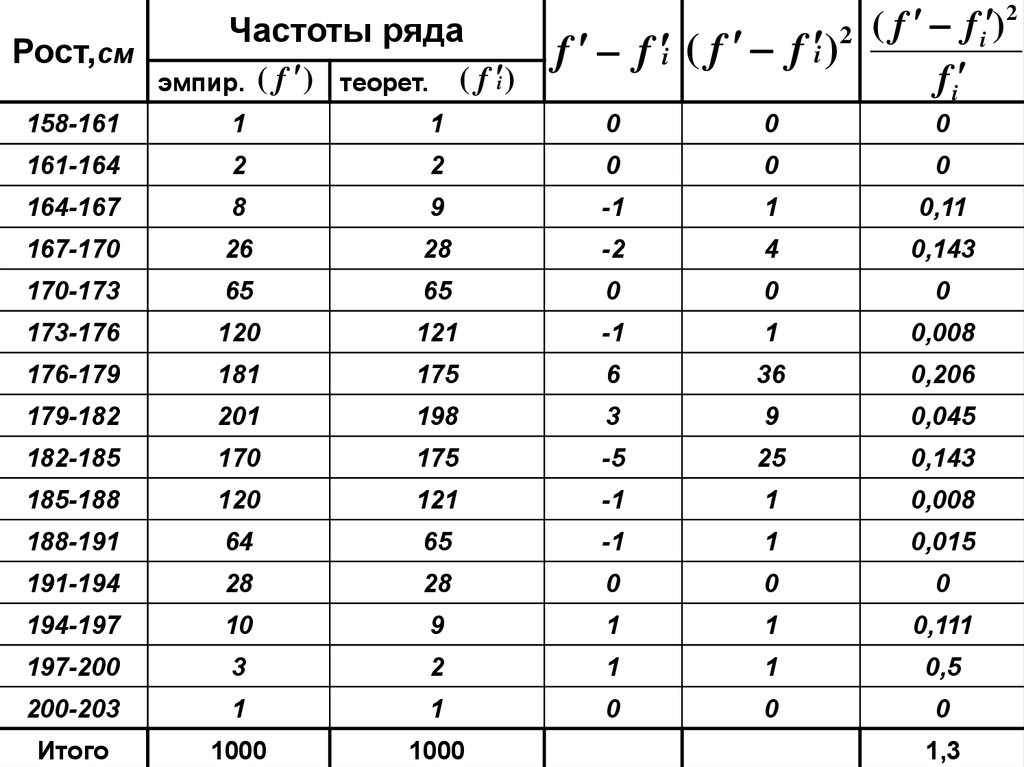
Mo 14 2
15,3%
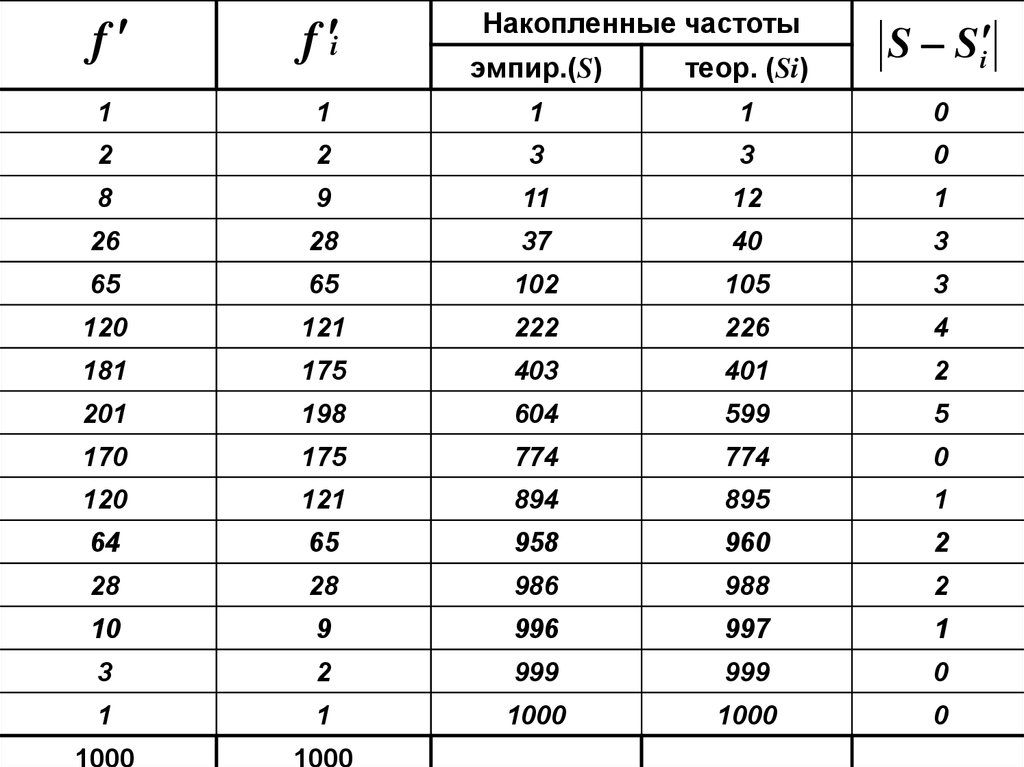
( 30 20) ( 30 25)
6.
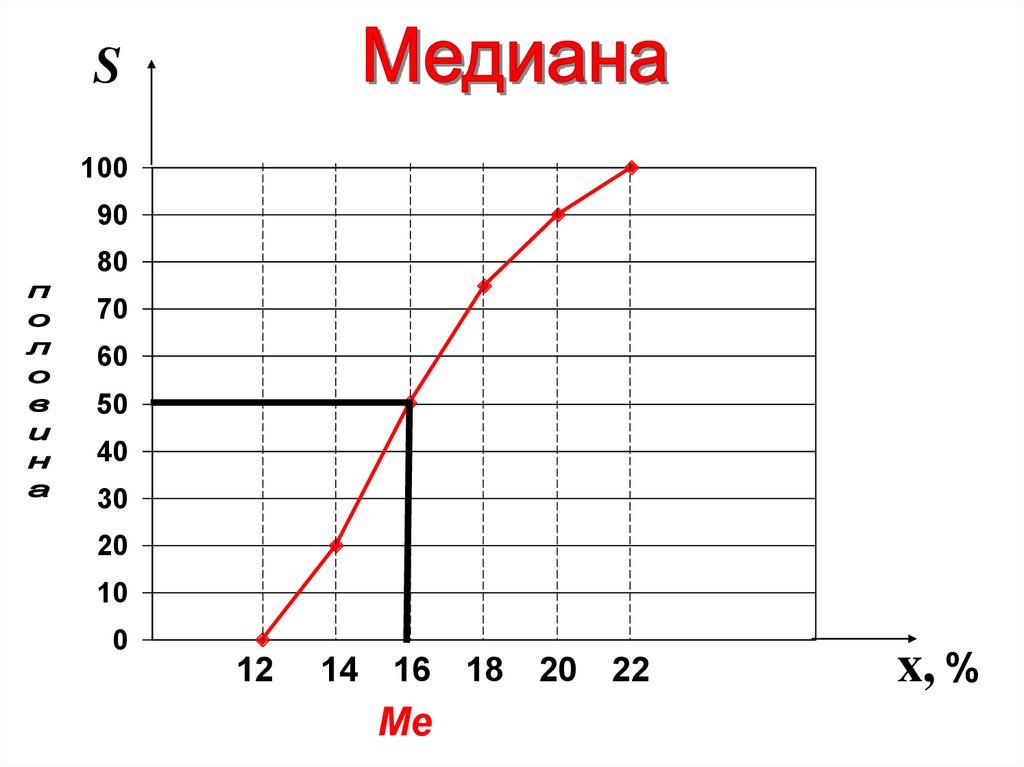
Me xm 1xm xm 1
Me
2
7.
1) 11 рабочих, имеющих тарифный разряд:5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5
Ранжирование по разряду:
2, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6
5ый разряд - центральный и медианный
8.
2) Если ранжированный ряд включает12 рабочих:
2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6
4 5
Me
4,5
2
разряда
9.
№п/п
1
2
3
4
… 50
51 … 99
100
Усл.
100 104 104 107 … 162 164 … 200 50000
ед.
Средний доход = 600-700 усл. ед.
Медиана = 163 усл. ед.
10.
n 1№Me
2
Где n – число единиц совокупности
100 1
№Me
50,5
2
11.
m1
f
i
S
Me
1
2 1
Me x 0 i
fMe
x0 и i
fMe
SMe-1
– соответственно нижняя граница и
величина медианного интервала
– частота медианного интервала
– накопленная частота предмедианного
интервала
12.
100 1№Me
50,5%
2
Интервал
16-18
50 50
Me 16 2
16%
25
13.
3( x Me ) x Mo1630
x
16,3%
100
3(16,3 16) 16,3 15,3
14.
f35
Самый высокий
30
25
20
15
10
5
0
12
14
16
Mo
18
20
22
x, %
15.
S100
90
80
70
60
50
40
30
20
10
0
12
14
16
Me
18
20
22
x, %
16.
R x max x min17.
nd
m
xi x
1
n
x xf
i
d
i
1
m
f
i
1
18.
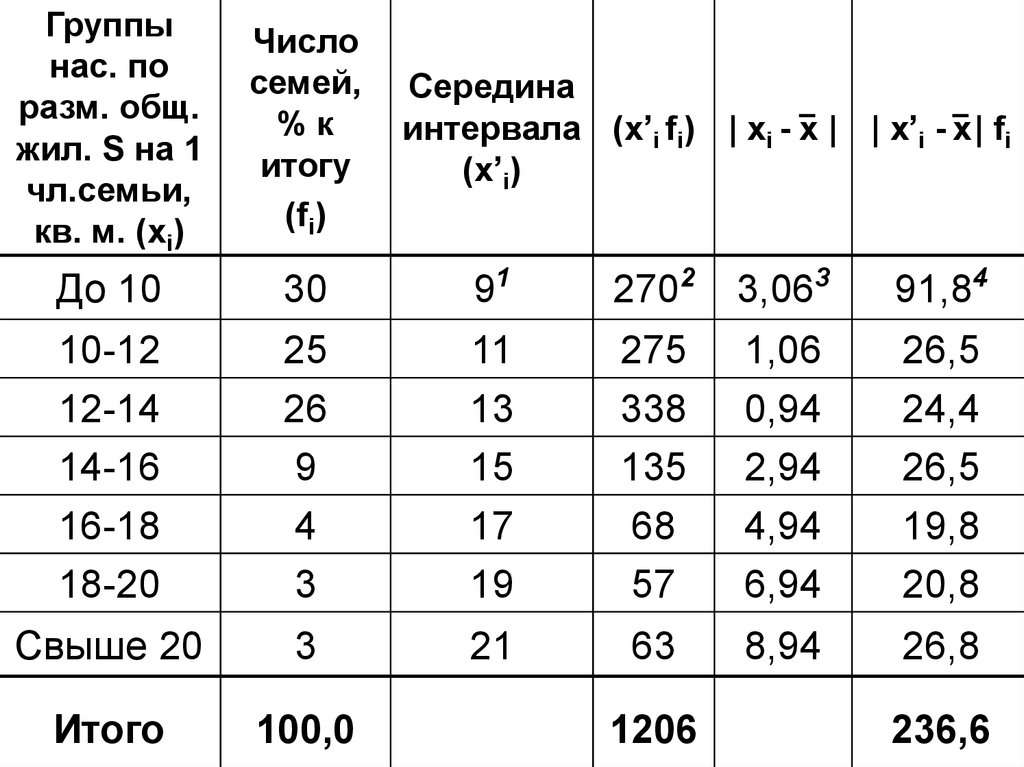
Группынас. по
разм. общ.
жил. S на 1
чл.семьи,
кв. м. (хi)
Число
семей,
%к
итогу
(fi)
До 10
30
91
2702
3,063
91,84
10-12
12-14
14-16
16-18
18-20
25
26
9
4
3
11
13
15
17
19
275
338
135
68
57
1,06
0,94
2,94
4,94
6,94
26,5
24,4
26,5
19,8
20,8
Свыше 20
3
21
63
8,94
26,8
Итого
100,0
Середина
интервала (х’i fi) | хi - x | | х’i - x | fi
(х’i)
1206
236,6
19.
1) Найдем середину интервалов (x’i)До 10
8 10
9
2
20.
2) Определим произведения значенийсередины интервалов (x’i ) на
соответствующие им веса
30 9 270
Рассчитаем среднюю величину по формуле
средней арифметической взвешенной
xf
x
f
i i
i
1206
2
12,06 м
100
21.
3) Найдем абсолютные отклонениясередины интервалов, принятых в качестве
вариантов признака (xi) от средней
величины (х)
9 12,06 3,06
22.
4) Вычислим произведения отклонений|х’i - х| на их веса (fi)
3,06 30 91,8
Сумму произведений делим на сумму весов
236,6
2
d
2,366м
100
Отклонение от средней
в целом небольшое
23.
x d 12,06 2,366 9,694м2
Отличие от
средней
Совокупность в отношении признака
однородна, средняя - типична
24.
x xn
2
2
1
n
x x f
n
2
i
2
1
m
f
i
1
25.
nx x
k
2
i
i
i 1
n
x x
2
i 1
k
f
i
i 1
fi
26.
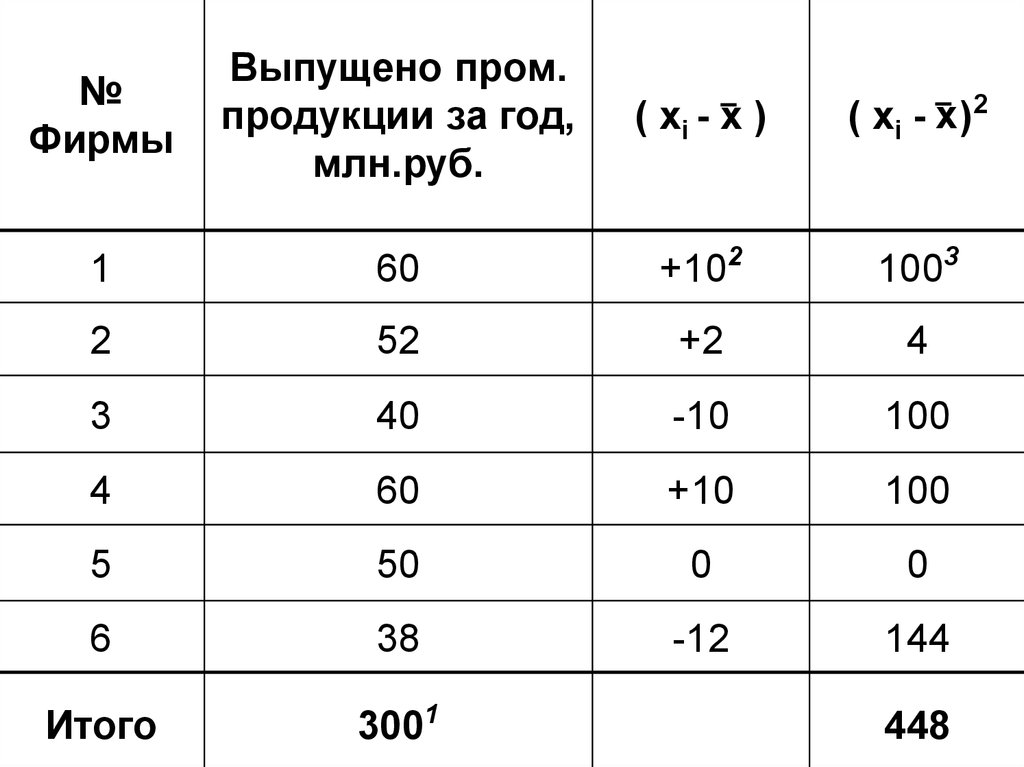
№Фирмы
Выпущено пром.
продукции за год,
млн.руб.
( хi - x )
( х i - x )2
1
60
+102
1003
2
52
+2
4
3
40
-10
100
4
60
+10
100
5
50
0
0
6
38
-12
144
Итого
3001
448
27.
1) Определим среднюю величину поисходным данным по формуле средней
арифметической простой (невзвешенной)
x
х
i
n
300
50 м лн. руб.
6
28.
2) Найдем отклонения60 50 10
3) Возведем отклонения во 2ую степень
10 100
2
4) Разделив сумму отклонений на число
единиц совокупности, получим дисперсию:
448
74,67
6
2
29.
5) Извлечем из дисперсии корень 2ойстепени, получим среднее
квадратическое отклонение
74,67 8,64 млн. рублей
Степень вариации невелика,
совокупность однородна
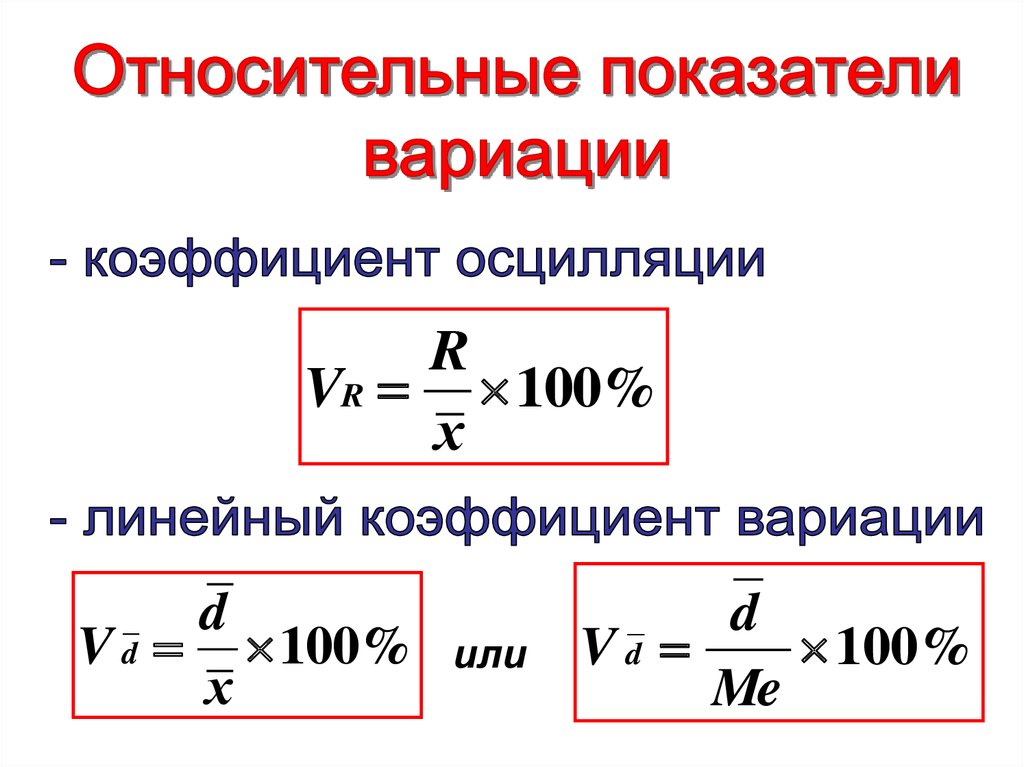
30.
RVR 100%
х
d
V d 100%
х
или
d
Vd
100%
Me
31.
Vx
100%
Совокупность считается однородной, если
коэффициент вариации не превышает 33 %
32.
2xi A
fi
k
2
2
2
i 1
k
x
A
k
fi
k
i 1
xi A
1 k fi
x
k A
m
fi
m
1
33.
22
Серед.
x
'
i
A
x' i A
x' i A x' i A
fi
fi
интерв. х’I - А
k k
k
k
(хi)
Рост
(х)
Колво
(fi)
158-161
1
159,5
-21
-7
-7
49
49
161-164
2
162,5
-18
-6
-12
36
72
164-167
8
165,5
-15
-5
-40
25
200
167-170
26
168,5
-12
-4
-104
16
416
170-173
65
171,5
-9
-3
-195
9
585
173-176
120
174,5
-6
-2
-240
4
480
176-179
181
177,5
-3
-1
-181
1
181
179-182
201
180,5
0
0
0
0
0
182-185
170
183,5
3
1
170
1
170
185-188
120
186,5
6
2
240
4
480
188-191
64
189,5
9
3
192
9
576
191-194
28
192,5
12
4
112
16
448
194-197
10
195,5
15
5
50
25
250
197-200
3
198,5
18
6
18
36
108
200-203
1
201,5
21
7
7
49
49
Итого
1000
10*
4064**
34.
A =180,5 – середина (x’i )k =3 – шаг интервала
xi A
1 k fi
*x
k A
m
fi
m
1
10
3 180,5 180,53см
1000
35.
2x' i A
fi
2
k
2
2
1
* *
k x A
m
fi
m
1
4064 2
2
3 (180,53 180,5) 36,5751
1000
36,5751 6,05см
2
Отклонение от
ср-й
36.
обладающих данным признакомm
p
n
q – доля единиц в совокупности,
p q 1
p – доля единиц в совокупности,
не обладающих данным признаком
1p 0 p
x
p
p q
Среднее значение
альтернативного признака
37.
1 p2
2
p (0 p) q q p p q
pq
p q
p q
2
2
2
pq
Дисперсия альтернативного признака
Предельное значение
2 0,25 при p 0,5
38.
Из них продукция:Партия
Готовая
продукция
Годная
Бракованная
1
1200
800
400
2
1000
840
160
3
1100
1000
100
39.
*Средний % годной продукции800 840 1000
2640
p
0,8 или 80%
1200 1000 1100 3300
*Средний % браковой продукции
q 1 0,8 0,2 или 20%
*Дисперсия удельного веса годной продукции
pq 0,8 0,2 0,16
2
40.
*Среднее квадратическое отклонениеудельного веса годной продукции
pq 0,16 0,4
*Коэффициент вариации удельного веса
годной продукции в общем выпуске продукции
0,4
V
100% 50%
x p 0,8
41.
kx x n
2
i
2
o
i 1
k
n
i
i 1
i
42.
kx x n
2
j
2
x
o
j 1
k
n
j
j 1
j
k – число групп
nj – число единиц в
j-ой группе
xj – частная средняя
по j-ой группе
xo – общая средняя по
совокупности единиц
43.
njx
ij
2
j
xj
i 1
nj
2
44.
k2
j 1
k
2
j
nj
n
j 1
j
45.
o2
2
2
46.
2o
2
2
47.
2o
2
Изменяется от 0 до 1
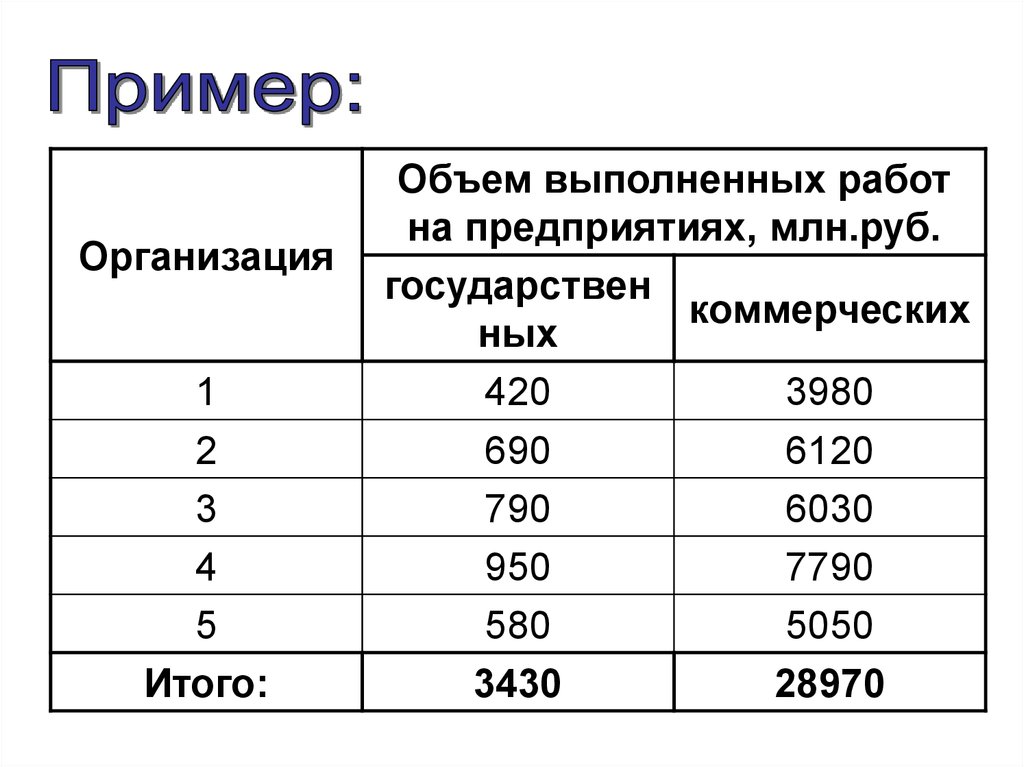
48.
Организация1
2
3
4
5
Итого:
Объем выполненных работ
на предприятиях, млн.руб.
государствен
коммерческих
ных
420
3980
690
6120
790
6030
950
7790
580
5050
3430
28970
49.
1) Определим общую среднюю:хo
x
n
i
i
3430 28970
5 5
32400
3240 млн . руб .
10
50.
2) Определим среднюю по каждой группе:3430
х1
686 млн . руб .
5
28970
х2
5794млн . руб .
5
51.
3) Рассчитаем внутригрупповые дисперсии:12
2
x
i
x
1
n1
(420 686) 2 (690 686) 2 (790 686) 2
5
(950 686) 2 (580 686) 2
5
162520
32504
5
52.
3) Рассчитаем внутригрупповые дисперсии:2
2
x x
i
1
2
n1
(3980 5794) 2 (6120 5794) 2 (6030 5794) 2
5
(7790 5794) 2 (5050 5794) 2
5
7990120
1598024
5
53.
4) Рассчитаем общую дисперсию:02
2
x
i
x
0
n0
(420 3240) 2 (690 3240) 2 (790 3240) 2
10
(950 3240) 2 (580 3240) 2 ( 3980 3240) 2
10
(6120 3240) 2 (6030 3240) 2 (7790 3240) 2
10
(5050 3240) 2
73381800
7338180
10
10
54.
5) Рассчитаем среднюю извнутригрупповых дисперсий:
2
1598024 5 32504 5
815264
10
55.
6) Рассчитаем межгрупповуюдисперсию:
2
(686 3240) 2 5 (5794 3240) 2 5
6522916
10
56.
7) Найдем общую дисперсию поприему сложения дисперсий
815264 6522916 7338180
2
0
57.
8) Рассчитаем коэффициент детерминации6522916
0,889или88,9%
7338180
2
9) Определим эмпирическое корреляционное
отношение
0,889 0,94
58.
Pi (1 Pi )2
Pi
Pi – доля изучаемого признака в
отдельных группах
59.
P (1 P )nn
i
2
Pi
i
i
i
i
i
Pi (1 Pi )
60.
( Pi P ) ni2
2
Pi
i
n
Pn
p
n
i i
i
i
i
i
ni – численность
единиц в отдельных
группах
i
P – доля изучаемого
признака во всей
совокупности
61.
P (1 P )2
P
62.
ЦехУдельный вес
основ. рабочих,
%, Pi
Численность
рабочих,
чел., n
1
80
100
2
75
200
3
95
150
Итого:
450
63.
1) Определяем долю изучаемого признака всовокупности в целом
0,80 100 0,75 200 0,90 150
P
0,81
450
2) Определяем общую дисперсию доли
0,81 (1 0,81) 0,154
2
P
64.
3) Определяем внутригрупповые дисперсии2
P1
0,8 (1 0,8) 0,16
2
P2
0,75 (1 0,75) 0,19
2
P3
0,9 (1 0,9) 0,09
4) Вычисляем среднюю из внутригрупповых
дисперсий
0,16 100 0,19 200 0,09 150
0,15
450
2
Pi
65.
5) Определяем межгрупповую дисперсиюPi2
(0,8 0,81) 2 100 (0,75 0,81) 2 200 (0,9 0,81) 2 150
450
Pi2 0,004
Проверка :
0,154 0,15 0,004
66.
Q1 xQ1 iQ 3 xQ 3 i
1
f S
4
Q1 1
fQ1
3
f S
4
fQ 3
Q3 1
67.
xQ1 – нижняя граница интервала,содержащего нижний квартиль (интервал
определяется по накопленной частоте, 1ой
превышающей 25%)
xQ3 – нижняя граница интервала,
содержащего верхний квартиль (интервал
определяется по накопленной частоте, 1ой
превышающей 75%)
i – величина интервала
68.
SQ1-1 – накопленная частота интервала,предшествующего интервалу,
содержащему нижний квартиль
SQ3-1 – накопленная частота интервала,
предшествующего интервалу, содержащему
верхний квартиль
fQ1 – частота интервала, содержащего
нижний квартиль
fQ3 – частота интервала, содержащего
верхний квартиль
69.
Группы банков посрокам
Число банков, Накопленная
функционирования,
% к итогу
частота, S
лет, х
1-2
10
10
2-3
15
25
3-4
21
46
4-5
25
71
5-6
12
83
6-7
7
90
7-8
5
95
Свыше 8
5
100
Итого:
100
70.
100 1N Q1
25,3
4
100 1
NQ3
3 75,8
4
3 Q1 4
5 Q3 6
100 25
4
Q1 3 1
3года
21
100 3 71
4
Q3 5 1
5,3года
12
71.
1 f S d 1 1d1 xd 1 i 10
f d1
d 2 xd 2 i
d 9 xd 9 i
2
f S
10
d 2 1
fd 2
9
f S
10
fd 9
d 9 1
72.
100 1N d1
10,1
10
100 1
Nd 9
9 90,9
10
100 10
10
2 d1 3 d1 2 1
2года
15
100 9 90
10
7 d9 8 d9 7 1
7 лет
5
73.
SPn L ( ) (i )
f
74.
Pn – обозначение n-ого перцентиляL – нижняя граница интервала
S – число оценок, необходимое, чтобы
попасть в точку на горизонтальной оси,
которая соответствует данному
перцентилю
i – расстояние от нижней границы L до
верхней границы L+1 (шаг интервала)
f – число оценок, расположенных в
интервале от L до L+1
75.
170,34
50
34% оценок в распределении
ниже оценки студента
Иванова
1
0,02
50
2% от всех оценок
распределения составляет
оценка студента Иванова
34 2 : 2 35
Перцентильный ранг
оценки студента Иванова
76.
77.
Q11
Q 3 Q1
Q3
KV
Q1
Q3 Q2
1
Q3
V KV 1,5
в большинстве случаев
78.
d9Kd
d1
Не совсем точен: сопоставляется
min и max величины
79.
x maxKФ
x min
1
xj
n j
1
xS
n S
x
x
j
j
S
S
80.
Xjj
– сумма значений признака 10% самых
крупных единиц в совокупности
n – число единиц совокупности
самых крупных и мелких
s
Xs
– сумма значений признака 10%
самых мелких единиц в совокупности
81.
Капитал, млн.руб.:1) 6,9
6) 3,7
11)10,9
16)8,1
2) 9,3
7) 5,1
12)7,2
17)2,1
3) 1,3
8) 2,9
13)3,2
18)4,3
4) 6,0
9) 1,4
14)8,9
19)4,5
5) 13,4
10)1,6
15)1,2
20)11,5
82.
120 2ед.
10
10% самых крупных и
10% самых мелких
банков
(11,5 13,4) / 2 12,45
KФ
9,96 раза
(1,2 1,3) / 2
1,25
Уровень дифференциации
достаточно высок
83.
M k ( x A)k
( x A)
f
j
Mk
i
i
i
k
fi
84.
A 0x f
f
i
Mk ( xi 0)
k
k
i
i
j
j
85.
A xo (Производная величина)(x x )
f
i
Mk ( xi xo )
k
o
i
j
j
k
fi
86.
A x (Средняя арифметическая)( x x)
f
i
Mk ( xi xk )
k
i
j
j
k
fi
87.
ВидыПорядок
Начальные Центральные
x f
( x x)
M
x M
f
f
( x x)
x f
M
x M
f
f
x f
( x x)
M
x M
f
f
i
1-ый
i
i
i
1
j
j
i
2-ой
2
2
i
2
i
i
i
3-ий
3
i
3
i
j
4
x
i
fi
i
f
j
j
3
i
M2
j
2
(
x
i
A
)
fi
i
3
fi
j
M3
j
x4 M4
4
(
x
i
x
)
fi
i
f
j
j
f
j
j
i
j
4-ый M 4
i
j
j
3
fi
j
j
fi
j
i
2
( x A)
f
i
M1
j
j
2
fi
i
1
Условные
3
(
x
i
A
)
fi
i
f
j
j
M4
4
(
x
i
A
)
fi
i
f
j
j
88.
Asx Mo
ИЛИ
As
x Mе
89.
As>0As<0
Правосторонняя
ассиметрия
Левосторонняя
ассиметрия
90.
AsM3
3
Ассиметрия выше 0,5 считается
значительной, меньше 0,25 незначительной
91.
As6(n 1)
(n 1)( n 3)
92.
ASAs
3
Ассиметрия существенна и
распределение признака в
ген. совокупности
несимметрично
93.
РазмерСере
Число
кредита,
дина
банков
млн.руб
инт.
(f)
(x)
(x’)
X’i fi Х’i – X (Х’i – X)2 fi (Х’i – X)3 fi
1-6
6
3,5
21
-10
600
-6000
6-11
3
8,5
25,5
-5
75
-375
11-16
11
13,5 148,5
0
0
0
16-21
5
18,5
92,5
5
125
625
21-26
5
23,5 117,5
10
500
5000
Итого:
30
405,5
1300
-750
94.
xx
i
fi
M2
M3
2
fi
405
13,5
30
( x x )
i
2
fi
fi
750
25
30
fi
( x x )
i
fi
3
1300
43,33
30
95.
AsM3
3
25
25
0,09
3
(6,58)
284,89
Незначительная по величине
и отрицательная по
характеру ассиметрия
96.
EkM4
4
3
В нормальном распределении Ek=0
97.
Ek>0Ek<0
Островершинное
распределение
Плосковершинное
распределение
98.
Ek24n( n 2)( n 3)
2
( n 1) ( n 3)( n 5)
Где n – число наблюдений
99.
yt1
e
2
1 2
t
2
100.
y t – ордината кривой нормальногораспределения
x x
t
– стандартизированное отклонение
δ
e
и
– материальные постоянные
(= 2,7182 и 3,1415 соответственно)
x
– варианты вариационного ряда
x
– их средняя величина
– среднее квадратическое отклонение
101.
Крепость Число Сереодиночн. образ дина
нити, г
цов
инт.
(x’)
(x)
(f)
t
x– x
x x
δ
f (t )
1 12 t 2
e
2
fm
k f
f (t )
исчисл округ
ение ление
56-58
5
57
-7,66 2,473 0,018884
6,15
6
58-60
29
59
-5,66 1,83
0,07477
24,1
24
60-62
63
61
-3,66 1,18
0,19886
64,2
64
62-64
117
63
-1,66 0,54
0,34482
111,2
111
64-66
116
65
0,34
0,11
0,39654 127,9
128
66-68
102
67
2,34
0,75
0,30114
97,1
97
68-70
48
69
4,34
1,40
0,14973
48,3
48
70-72
14
71
6,34
2,04
0,04980
16,1
16
72-74
6
73
8,34
2,69
0,01071
3,5
4
Итого:
500
498,5
498
102.
1) x 64,66 г2) 3,1г
3)нормированное отклонение (t)
57 64,66 7,66
2,47
2,47
3,1
3,1
4)по приложению значения плотности
вероятности для нормированного
нормального закона распределения
2 500
6,1 0,01888
6
3,1
103.
fi130
120
110
100
90
80
70
60
50
40
30
20
10
0
эмпирические
теоретические
x
57
59
61
63
65
67
69
71
73
крепость
одиночной нити, г
104.
( fэ fm )fm
2
2
fэ и fm – эмпирические и теоретические
частоты соответственно
105.
Вероятность P ( ) определенияпо приложению:
2
P 0,5
– эмпирические и
теоретические
распределения близки
P 0,2;0,5 – совпадение
удовлетворительное
В остальных
случаях
– совпадение
недостаточное
106.
с2
2
– число степеней свободы
C<3 – различие несущественное
107.
Df
Условие:
Большое число
наблюдений (не<100)
D – max значение разности между накопленными
эмпирическими и теоретическими частотами
Ef – сумма эмпирических частот
108.
Рост,смЧастоты ряда
эмпир.
( f )
( f i )
теорет.
2
(
f
f
)
2
i
f f i ( f f i )
f i
158-161
1
1
0
0
0
161-164
2
2
0
0
0
164-167
8
9
-1
1
0,11
167-170
26
28
-2
4
0,143
170-173
65
65
0
0
0
173-176
120
121
-1
1
0,008
176-179
181
175
6
36
0,206
179-182
201
198
3
9
0,045
182-185
170
175
-5
25
0,143
185-188
120
121
-1
1
0,008
188-191
64
65
-1
1
0,015
191-194
28
28
0
0
0
194-197
10
9
1
1
0,111
197-200
3
2
1
1
0,5
200-203
1
1
0
0
0
Итого
1000
1000
1,3
109.
1,32
(Критерий согласия Пирсона)
1,3 (15 3) 10,7
с
2,19
4,899
2(15 3)
(Критерий согласия Романовского)
110.
ff i
1
Накопленные частоты
эмпир.(S)
теор. (Si)
S Si
1
1
1
0
2
2
3
3
0
8
9
11
12
1
26
28
37
40
3
65
65
102
105
3
120
121
222
226
4
181
175
403
401
2
201
198
604
599
5
170
175
774
774
0
120
121
894
895
1
64
65
958
960
2
28
28
986
988
2
10
9
996
997
1
3
2
999
999
0
1
1
1000
1000
0
1000
1000
111.
max разрыв = 55
0,158 0,2
1000
(Критерий согласия Колмогорова)
Распределение нормальное,
отклонения эмпирических частот от
теоретических случайные


























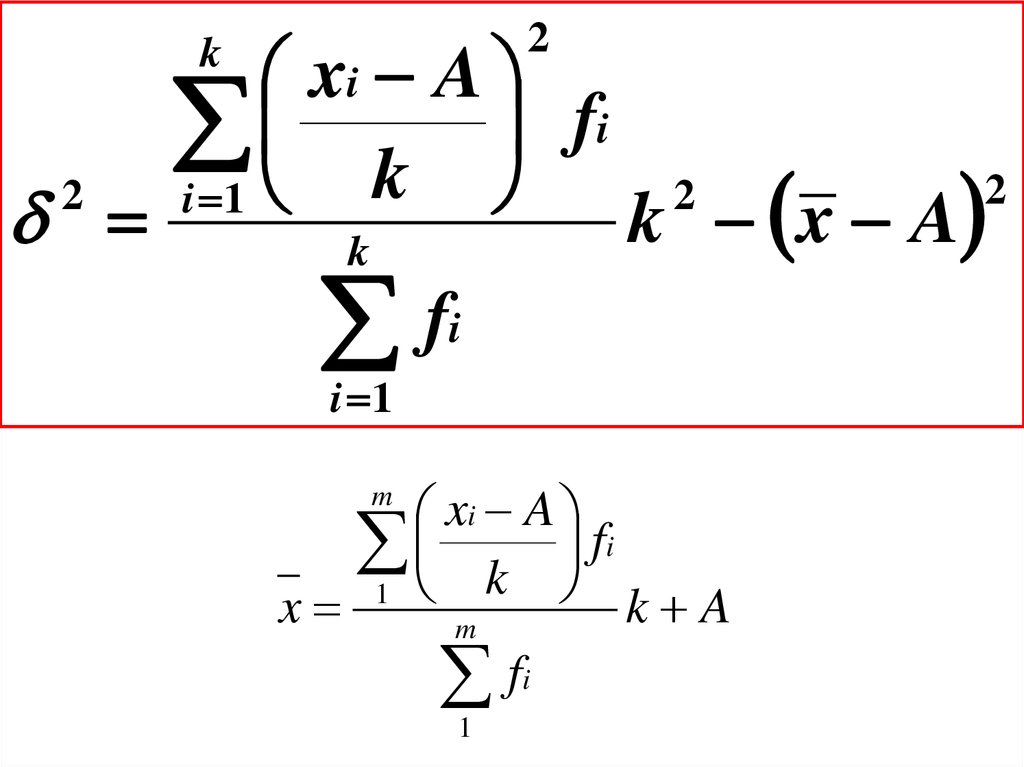






































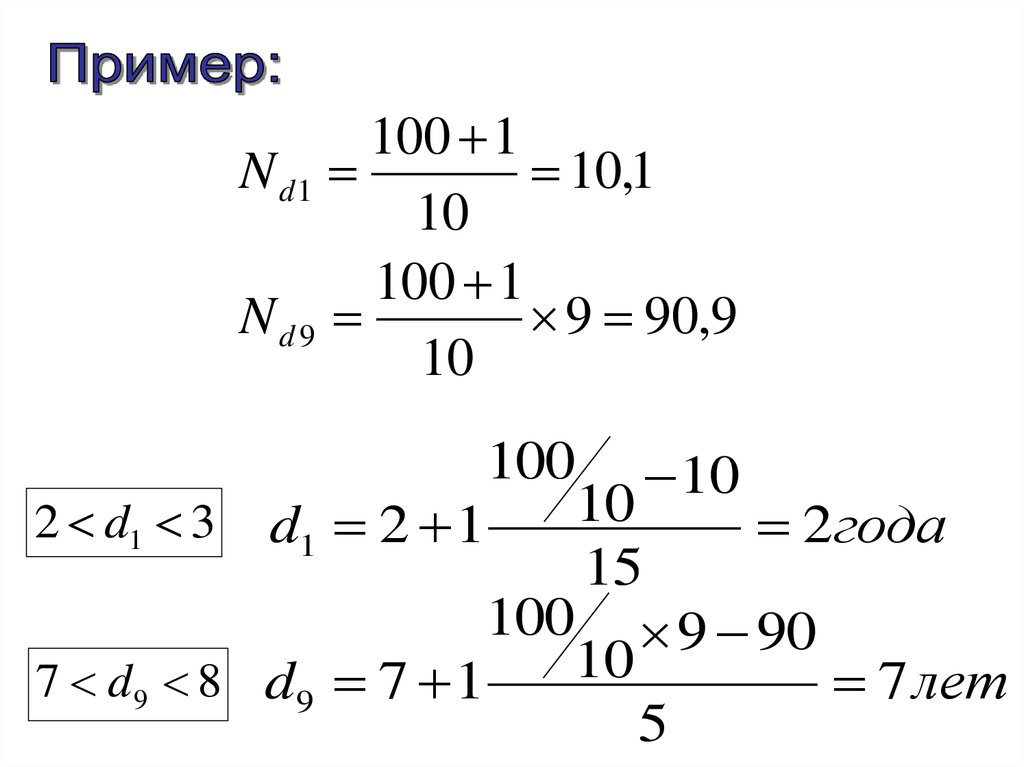




















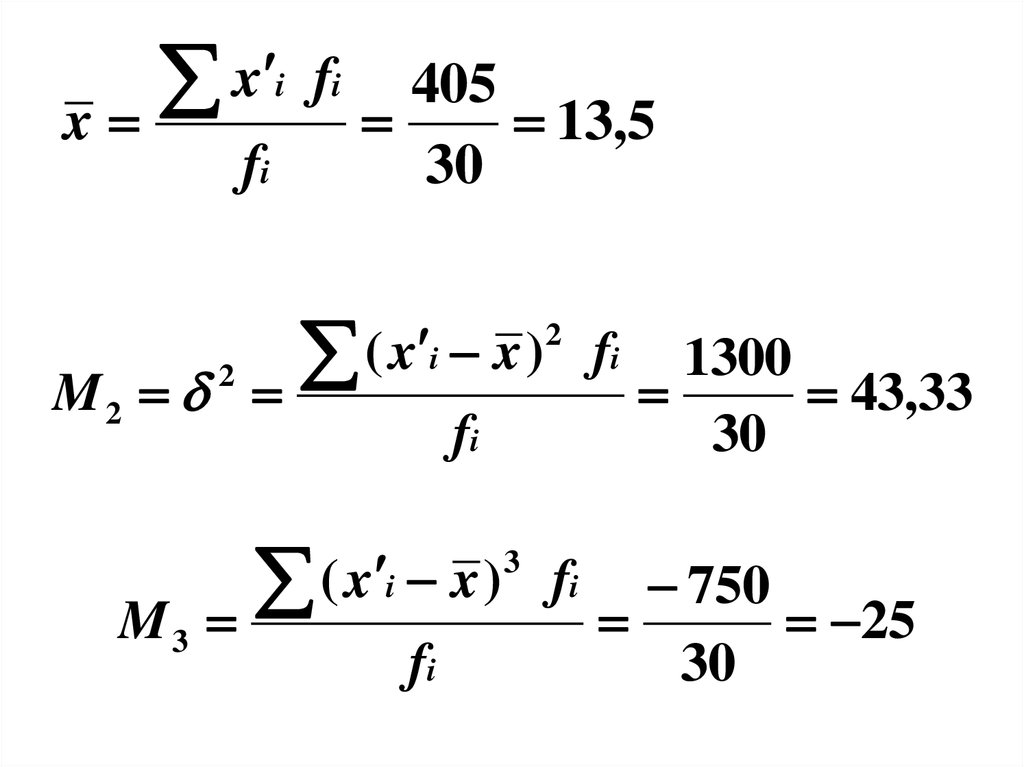














 mathematics
mathematics








