Similar presentations:
Показатели вариации
1. Показатели вариации
2. Содержание
1. Понятие и виды показателей вариации2. Правило сложения дисперсий
3. Особенности выборочного наблюдения
3.
Вариация признакаразличие в значениях признака у
отдельных единиц изучаемой
совокупности в статистике
(variatio – лат., изменение,
колеблемость, различие)
4.
Показатели вариацииАбсолютные
Относительные
5.
1. Абсолютные1.1. Размах вариации
R = xmax - xmin
Разность между
наибольшим и наименьшим
значениями варьирующего
признака
Показывает в каких
пределах колеблется
значение признака
НО: Улавливает только крайние отклонения, но не
отражает отклонений всех вариант в ряду.
6.
1.2. Среднеелинейное отклонение
Средняя арифметическая из
абсолютных значений
отклонений индивидуальных
значений варьирующего
признака от их средней
x x
d
x x f
d
f
i
n
i
i
НО: показатель не учитывает знаки отклонения
вариантов от средней
i
7.
1.3. ДисперсияСредний квадрат отклонений
значений вариантов от их
средней величины
xi x
2
2
n
x x * f
f
2
2
i
i
i
САМЫЙ ТОЧНЫЙ ПОКАЗАТЕЛЬ ВАРИАЦИИ
НО: дисперсия имеет квадрат размерности признака
8.
Свойства дисперсии1. Дисперсия постоянной величины равна нулю: D(а) = 0.
2. Дисперсия не меняется, если все варианты увеличить
(уменьшить) на одно и то же число: D(а + х) = Dх.
3. Если все варианты умножить на число а, дисперсия
увеличиться в а2 раз:
D(ах) = а2 Dх
Т.е. постоянный множитель выносится за знак дисперсии
возведенным в квадрат.
9.
Свойства дисперсии4. Свойство минимальности дисперсии: Дисперсия от
средней меньше, чем средний квадрат отклонений
индивидуальных значений признака от произвольной величины а
на величину (а - х )2.
Если У =
2
(
х
а
)
n
D У (а х )
, то
2
5. Дисперсия признака равна разности между средней из
квадратов индивидуальных значений признака и квадратом их
средней величины:
___
2
_
x (x)
2
10.
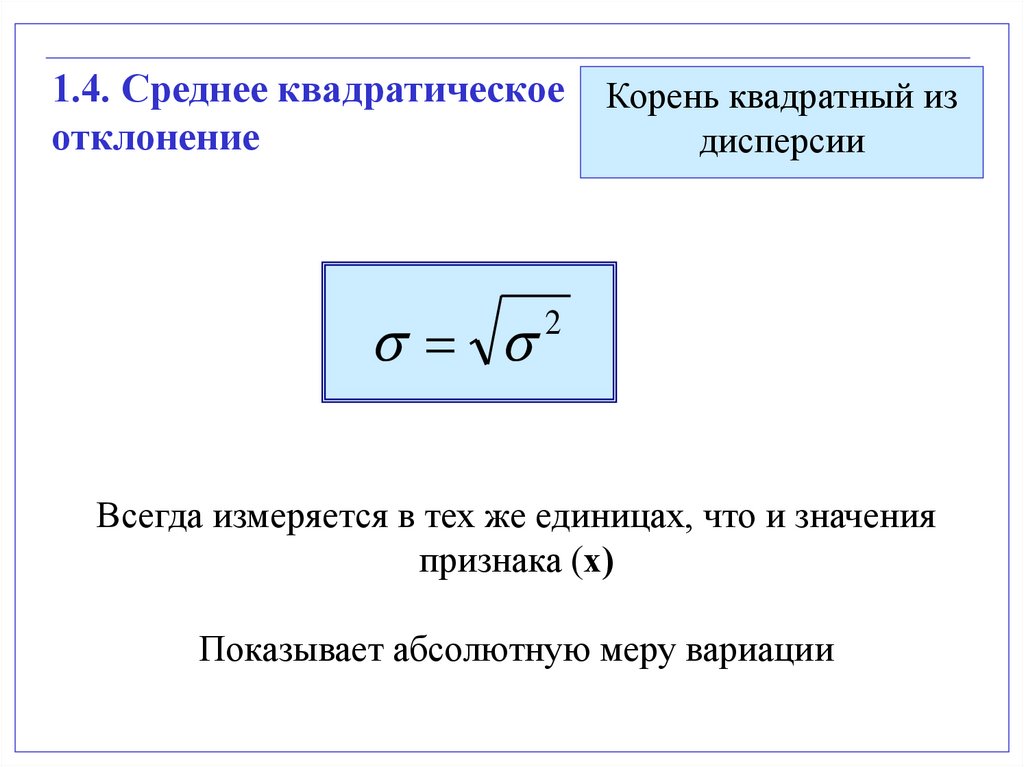
1.4. Среднее квадратическоеотклонение
Корень квадратный из
дисперсии
2
Всегда измеряется в тех же единицах, что и значения
признака (х)
Показывает абсолютную меру вариации
11.
2. Относительные2.1. Коэффициент
вариации
v 100
x
Отношение
среднеквадратического
отклонения к среднему
значению
На сколько процентов в среднем отклонялись
индивидуальные значения признака от среднего
Если коэффициент вариации не превышает 33%, то
совокупность считается однородной, и средняя,
рассчитанная для этой совокупности, является типичной
характеристикой этой совокупности
12.
Коэффициент вариации используется в экономическихрасчетах для оценки равномерности экономических
явлений, он выступает коэффициентом
неравномерности
Кравномерн = 100 -
Коэффициент вариации позволяет сравнивать степень
вариации признаков в разных совокупностях с
различающимися уровнями средних
13.
2.2. Линейный коэффициентвариации
2.3. Коэффициент осцилляции
d
Vd * 100
x
R
V R * 100
x
14.
Альтернативные признакитакие признаки, которыми одни
единицы изучаемой совокупности
обладают, а другие – нет, т.е. вариация
которых проявляется в том, что у
одних единиц они встречаются, а у
других отсутствуют
Например: наличие опыта работы у студентов, наличие
детей
15.
Обозначим:p+q=1
1 – наличие интересующего нас признака у единицы
совокупности;
0 – его отсутствие;
р – доля единиц, обладающих данным признаком;
q – доля единиц, не обладающих данным признаком
хf 1* р 0 * q
х
p
p q
f
Средняя и Дисперсия
x x * f (1 p) p (0 p) q q p p q pq(q p)
pq
p q
p q
p q
f
2
2
р
2
2
2
2
16.
Пример.На 10 000 человек населения района приходится 4500 мужчин
и 5500 женщин.
р = 4500 / 10000 = 0,45
q = 5500 / 10000 = 0,55
Дисперсия альтернативного признака:
pq 0,45 * 0,55 0,2475
2
р
Предельное значение дисперсии альтернативного признака
равно 0,25.
Оно получается при р = 0,5.
17.
1. Внутригрупповая дисперсияхарактеризует вариацию признака в каждой
группе под влиянием различных случайных
факторов, за исключением признака –
фактора, положенного в основание
группировки;
отражает случайную вариацию
ni
_
2
(
x
x
)
i i
i2 i 1
_
ni
x i - среднее значение признака в группе i,
ni - число единиц совокупности, попавших в группу i.
18.
Количество внутригрупповых дисперсий соответствуетколичеству групп, на которые разбита совокупность по
типическому признаку (т.е. по признаку-фактору).
Средняя из внутригрупповых дисперсия
i
2
i fi
i
f
i
i
i - дисперсия признака в i - группе,
f i - число единиц совокупности в i - группе.
19.
2. Межгрупповая дисперсияхарактеризует систематическую вариацию
результативного признака, обусловленную
влиянием признака-фактора, положенного в
основу группировки, т.е. отклонения
групповых средних от общей средней
_
_
( x x) f
f
2
i
i
_
х f
х
f
i
i
i
x_ i -
i
i
i
среднее значение признака в группе i,
x - общая средняя,
f i - число единиц совокупности в i - группе.
20.
3. Общая дисперсияхарактеризует вариацию, складывающуюся
под влиянием всех факторов
x x * f
f
2
2
i
i
i
_
x - общая средняя в изучаемой совокупности.
21.
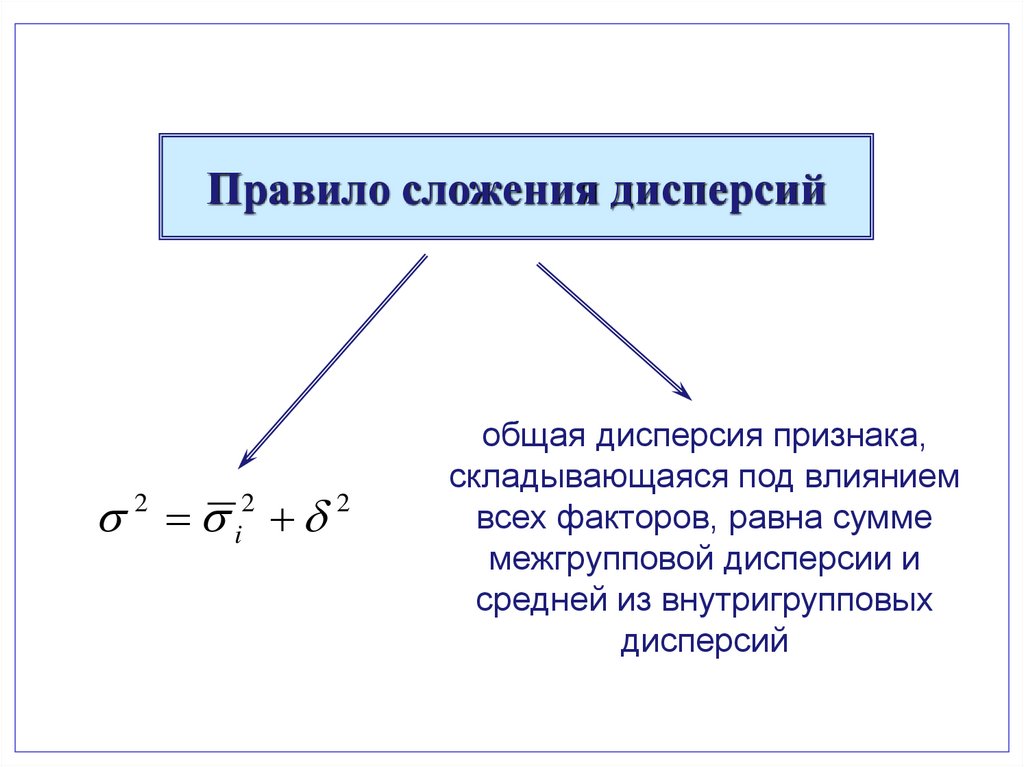
Правило сложения дисперсий2
2
i
2
общая дисперсия признака,
складывающаяся под влиянием
всех факторов, равна сумме
межгрупповой дисперсии и
средней из внутригрупповых
дисперсий
22.
Коэффициент детерминации –показывает удельный вес влияния факторного
признака в общей колеблемости изучаемого
явления
Эмпирическое корреляционное
отношение –
служит для оценки тесноты связи между
группировочным и результативным признаками
23.
= 0 – связь отсутствует (группировочный признак никак невлияет на образование общей вариации)
= 1 – связь функциональная (группировочный признак
целиком определяет вариацию изучаемого результативного
признака)
Чем ближе к 1, тем теснее, ближе к функциональной
зависимости связь между признаками
Для качественной оценки тесноты связи можно
воспользоваться соотношениями Чэддока:
Сила
связи
0,1 – 0,3
Слабая
0,3 – 0,5
Умеренная
0,5 – 0,7
Заметная
0,7 – 0,9
0,9 – 0,99
Тесная
Весьма
тесная
24.
Выборочное наблюдение –Наблюдение, при котором обследованию
подвергается часть единиц совокупности,
отобранных на основе научно разработанных
принципов, обеспечивающих получение
достоверных данных для характеристики
этой совокупности в целом
25.
Преимущества выборочного наблюдения передсплошным:
требуют значительно меньше сил, средств и времени,
чем сплошные,
позволяют достигнуть большей глубины и детальности
изучения вопроса при более высокой точности
регистрации фактов,
позволяют быстрее подводить итоги и более
тщательно организовать и провести наблюдение.
26.
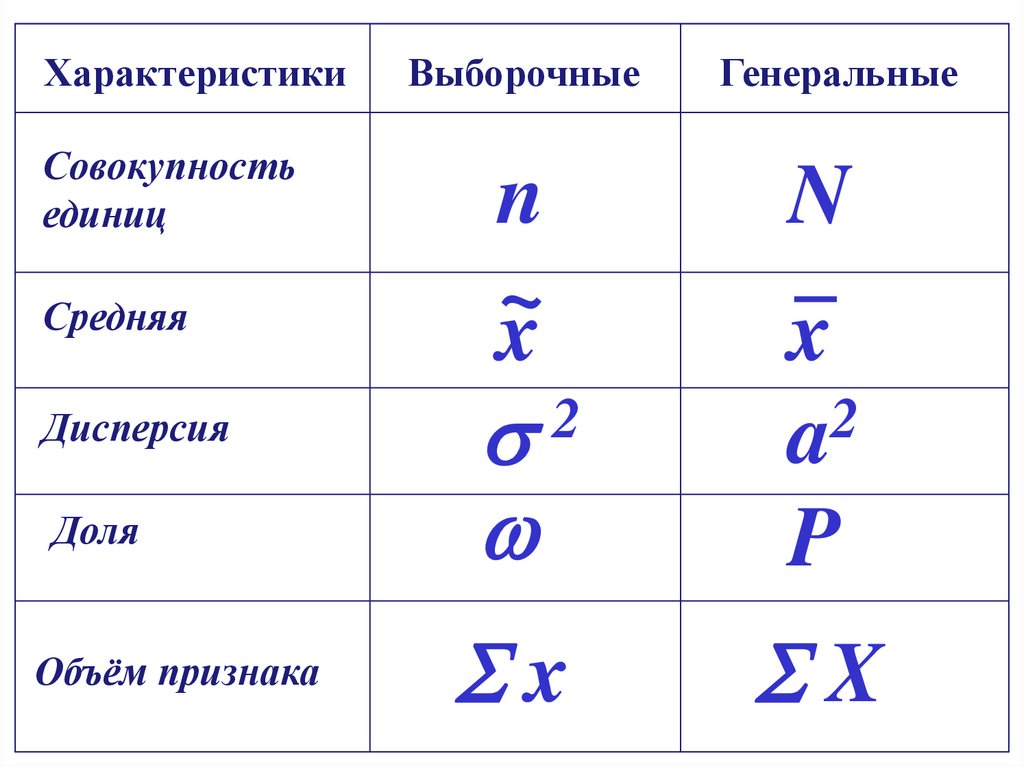
ХарактеристикиСовокупность
единиц
Выборочные
Генеральные
n
~
x
Доля
N
_
x
2
a
P
Объём признака
x
X
Средняя
Дисперсия
2
27.
Способы формирования выборочной совокупностиГрупповой отбор
Индивидуальный
отбор
в выборку
отбираются
отдельные единицы
в выборку попадают
качественно
однородные группы
или серии
изучаемых единиц
Комбинированный
отбор
28.
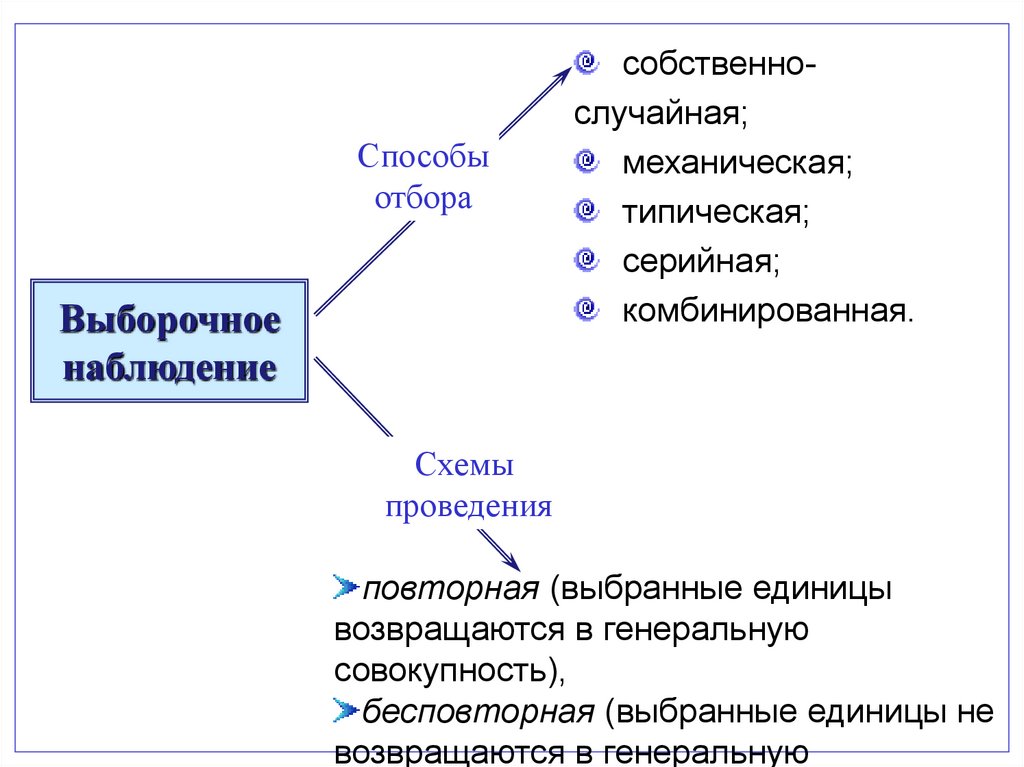
Способыотбора
Выборочное
наблюдение
собственнослучайная;
механическая;
типическая;
серийная;
комбинированная.
Схемы
проведения
повторная (выбранные единицы
возвращаются в генеральную
совокупность),
бесповторная (выбранные единицы не
возвращаются в генеральную
29.
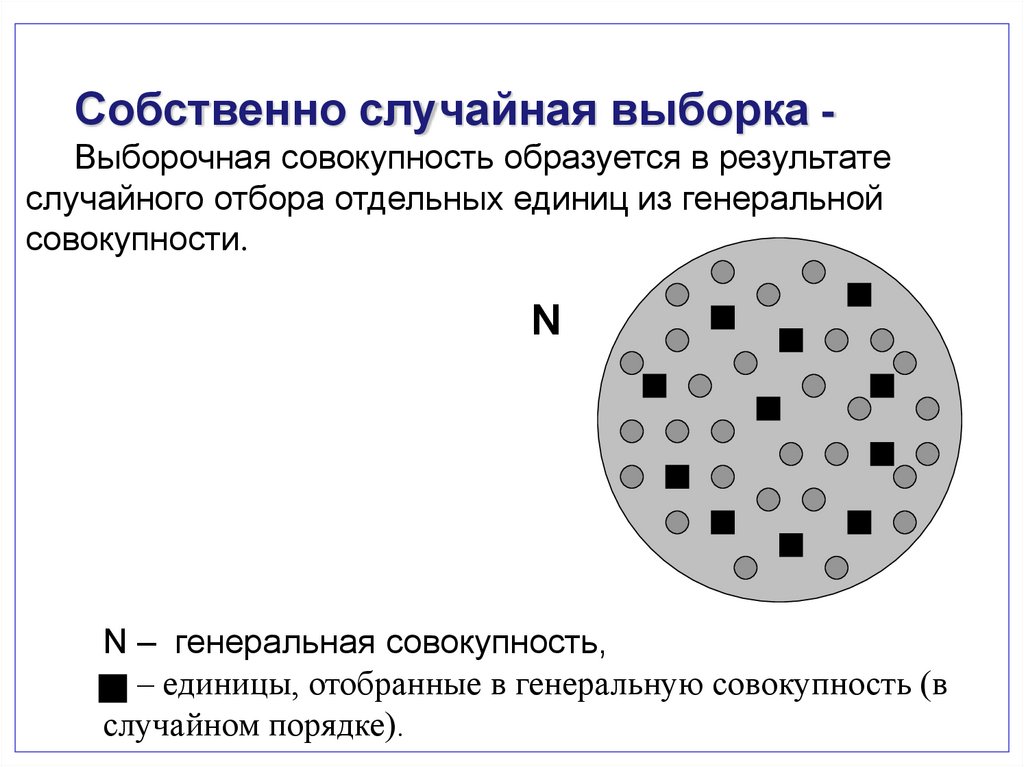
Собственно случайная выборка Выборочная совокупность образуется в результатеслучайного отбора отдельных единиц из генеральной
совокупности.
N
N – генеральная совокупность,
– единицы, отобранные в генеральную совокупность (в
случайном порядке).
30.
Механическая выборка Отбор единиц в выборочную совокупностьпроизводится из генеральной совокупности, разбитой на
равные интервалы. Размер интервала в генеральной
совокупности равен обратной величине доли выборки.
Например, при 2%-ой выборке отбирается каждая 50-я
единица (1:0,02).
Для обеспечения репрезентативности выборки все
единицы генеральной совокупности должны располагаться
в определенном порядке, т.е. должны быть упорядочены
по существенному, второстепенному или нейтральному
признаку.
1 группа
2 группа
1
2
3
4
5
6
7
8
9
10
31.
Типическая выборка Совокупность вначале расчленяется на однородныетипические группы, затем из каждой типической группы
собственно случайной или механической выборкой
производится индивидуальный отбор единиц
в выборочную совокупность
N
Серийная выборка Из генеральной совокупности отбираются не отдельные
единицы, а целые их серии (гнезда), внутри каждой из
попавшей в выборку серии обследуются все без
исключения единицы.
32.
Ошибка выборки определяетсянесколькими факторами:
1. размером выборки. Чем больше размер выборки
при прочих равных, тем меньше величина ошибки
выборки;
2. степенью варьирования изучаемого признака. При
одинаковом размере выборки ошибка выборки будет
меньше там, где изучаемый признак колеблется
(варьирует) в меньшей степени, т.е. совокупность более
однородна;
3. видом отбора – повторного или бесповторного. При
бесповторной выборке ошибка бесповторной выборки
меньше в (1 – n/N), где N – размер генеральной
совокупности, n – размер выборки;
4. надежности (уверенности), с которой хотим
33.
Утверждать, что выборочные характеристики будутотклоняться от генеральных на величину ошибки выборки,
можно не с абсолютной достоверностью, а лишь с
определенной степенью вероятности р.
Эта вероятность обуславливает появление в формулах
ошибки выборки множителя t, называемого
коэффициентом доверия.
Коэффициент
доверия
Вероятность
t=1
P = 0,683
t=2
P = 0,954
t=3
P = 0,997
34.
Формулы для расчета ошибки выборкиОшибки выборки
Метод отбора
для средней
повторный
t
для доли
wв 1 wв
t
n
2
n
wв 1 wв
2
n
n
t
1
бесповторный х t
1
N
N
n
n
35.
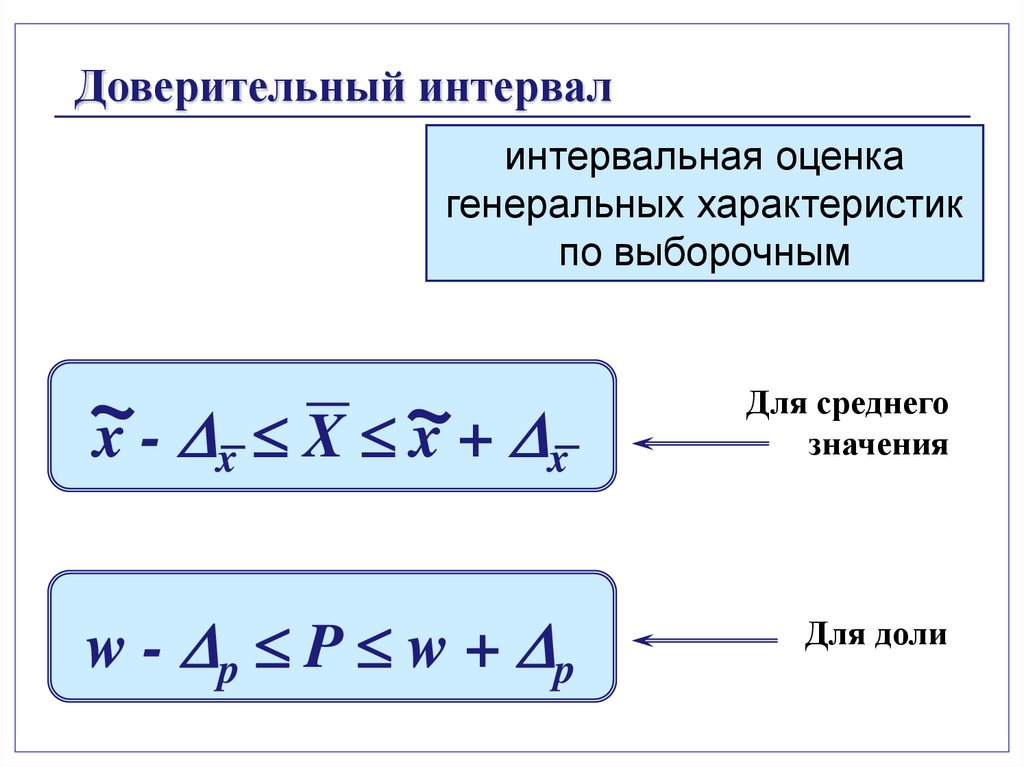
Доверительный интервалинтервальная оценка
генеральных характеристик
по выборочным
~x - x X ~x + x
Для среднего
значения
w - p P w + p
Для доли





























 mathematics
mathematics








