несобственный интеграл

1. Несобственные интегралы

b
Для существования
f ( x)dx
необходимы условия:
1) [a;b] – конечен, a
2) f(x) – ограничена (необходимое условие существования
определенного интеграла).
Несобственные интегралы – обобщение понятия определенного
интеграла на случай когда одно из этих условий не
выполнено.

2. 1. Несобственные интегралы I рода (по бесконечному промежутку)

Пусть y = f(x) непрерывна на [a;+ ).
y = f(x) непрерывна на [a;b], где b a .
b
существует
a
b
Имеем:
f ( x)dx.
f ( x)dx I (b) , D(I) = [a;+ ) .
a
ОПРЕДЕЛЕНИЕ. Несобственным интегралом I рода от
функции f(x) по промежутку [a;+ ) называется предел функции I(b) при b + .
Обозначают:
f ( x)dx
a

3.

Таким образом, по определению
b
f ( x)dx lim I (b) lim f ( x)dx
b
a
b
(1)
a
При этом, если предел в правой части формулы (1) существует
и конечен, то несобственный интеграл называют
сходящимся.
В противном случае (т.е. если предел не существует или равен
бесконечности)
несобственный
интеграл
называют
расходящимся.
Если y = f(x) непрерывна на (– ;b] , то аналогично определяется и обозначается несобственный интеграл I рода для
функции f(x) по промежутку (– ;b]:
b
b
a
f ( x)dx .
f ( x)dx alim

4.

Если y = f(x) непрерывна на ℝ , то несобственным интегралом
I рода для функции f(x) по промежутку (– ;+ ) называют
c
f ( x)dx f ( x)dx f ( x)dx ,
(2)
c
где c – любое число.
Несобственный интеграл от f(x) по промежутку (– ;+ )
называется сходящимся, если ОБА интеграла в правой части
формулы (2) сходятся.
В противном случае, несобственный интеграл по промежутку
(– ;+ ) называется расходящимся.
Будем рассматривать несобственные интегралы I рода по
промежутку [a;+ ). Для интегралов по промежутку (– ;b] и
(– ;+ ) все полученные результаты останутся справедливы.

5.

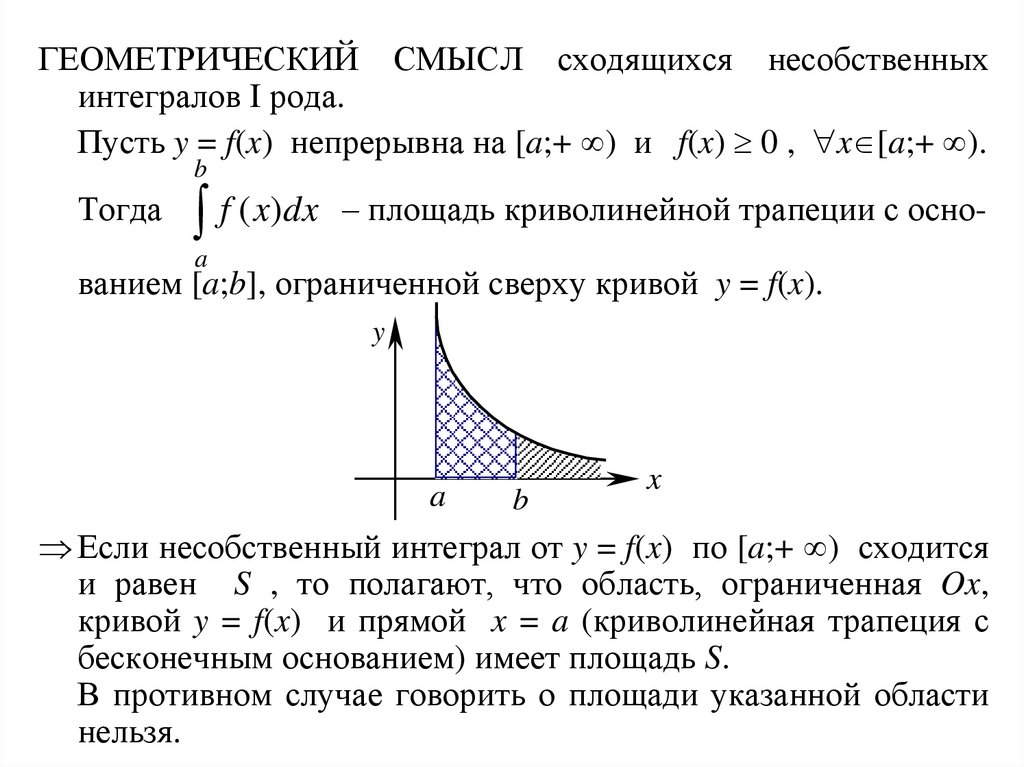
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ сходящихся несобственных
интегралов I рода.
Пусть y = f(x) непрерывна на [a;+ ) и f(x) 0 , x [a;+ ).
b
Тогда
f ( x)dx – площадь криволинейной трапеции с осноa
ванием [a;b], ограниченной сверху кривой y = f(x).
y
a
b
x
Если несобственный интеграл от y = f(x) по [a;+ ) сходится
и равен S , то полагают, что область, ограниченная Ox,
кривой y = f(x) и прямой x = a (криволинейная трапеция с
бесконечным основанием) имеет площадь S.
В противном случае говорить о площади указанной области
нельзя.

6.

На сходящиеся несобственные интегралы I рода переносятся
некоторые свойства определенных интегралов
(свойства 4, 5, 6, 7, 8).
Кроме того, для несобственных интегралов существует
обобщение формулы Ньютона – Лейбница.
Пусть F(x) – первообразная для f(x) на [a;+ ).
Тогда b [a;+ ) имеем
b
b
f ( x )dx F ( x ) a F (b) F (a )
a
b
lim f ( x)dx lim F (b) F (a)
b
a
b
f ( x)dx lim F (b) F (a)
a
b
(3)

7.

lim F (b) F (a) F ( x) a .
b
Обозначим
Тогда (3) примет вид:
f ( x)dx F ( x) a lim F ( x) F (a) .
a
x
(4)
Формулу (4) называют обобщением формулы Ньютона –
Лейбница для несобственных интегралов по промежутку
[a;+ ).
Аналогично для несобственных интегралов по промежутку
(– ;b] доказывается справедливость формулы
b
b
f ( x)dx F ( x) F (b) lim F ( x) .
x

8.

ПРИМЕРЫ. Вычислить несобственные
установить их расходимость:
1) cos xdx ;
0
0
dx
4)
;
2
4 x
xdx
7)
.
2
1 x
dx
2) n dx ;
x
a
(a 0)
0
5) e x dx ;
интегралы
3) e x dx ;
0
6) e x dx .
или

9. 2. Признаки сходимости несобственных интегралов I рода

ТЕОРЕМА 1 (первый признак сравнения).
Пусть f(x) и (x) непрерывны на [a;+ ) и
0 f(x) (x) , x [c; + ) (где c a).
Тогда:
1) если
( x)dx – сходится, то f ( x)dx тоже сходится,
a
причем
c
c
a
f ( x)dx ( x)dx ;
2) если
f ( x )dx – расходится, то
a
ходится.
( x)dx тоже расa

10.

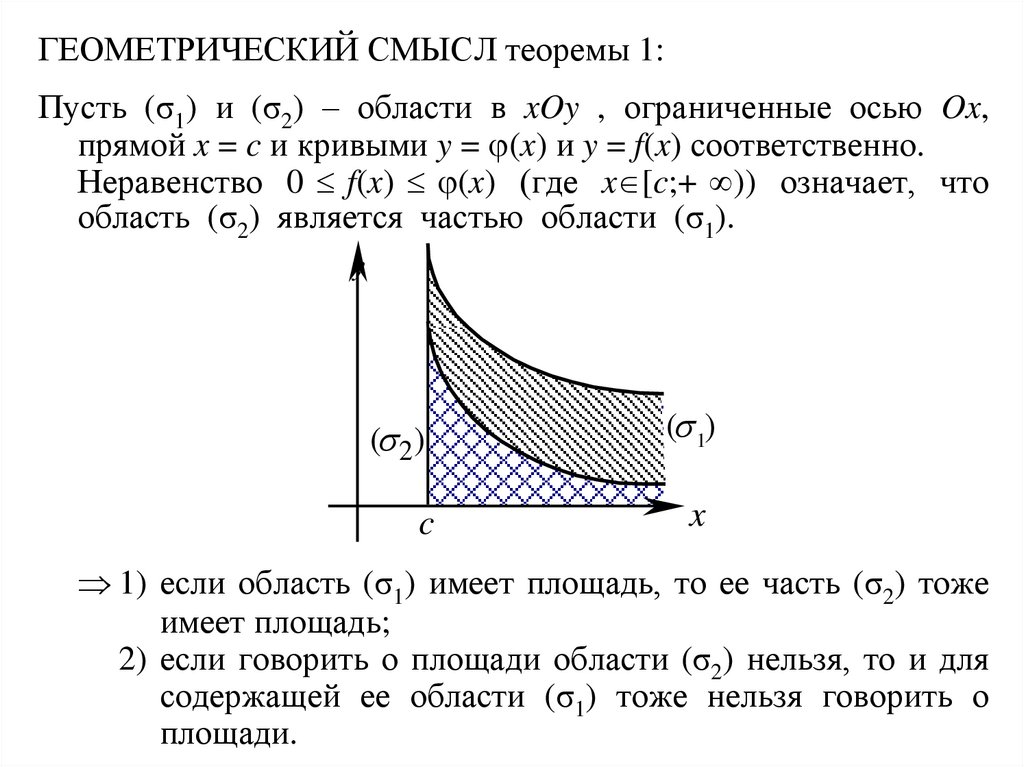
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ теоремы 1:
Пусть (σ1) и (σ2) – области в xOy , ограниченные осью Ox,
прямой x = c и кривыми y = (x) и y = f(x) соответственно.
Неравенство 0 f(x) (x) (где x [c;+ )) означает, что
область (σ2) является частью области (σ1).
y
( 2 )
( 1)
c
x
1) если область (σ1) имеет площадь, то ее часть (σ2) тоже
имеет площадь;
2) если говорить о площади области (σ2) нельзя, то и для
содержащей ее области (σ1) тоже нельзя говорить о
площади.

11.

ТЕОРЕМА 2 (второй признак сравнения)
Пусть f(x) и (x) непрерывны и неотрицательны на [a;+ ).
f ( x)
Если lim
h , где h – действительное число, отличное
x ( x)
от нуля, то интегралы
f ( x)dx
a
и
( x)dx
a
ведут себя одинаково относительно сходимости.

12.

Замечания.
1) Теорема 2 остается справедливой и в том случае, если f(x) и
(x) непрерывны и СОХРАНЯЮТ ЗНАК на [a;+ ).
2) При использовании теорем 1 и 2 в качестве «эталонных»
интегралов обычно используют следующие несобственные
интегралы:
сходится, при n 1,
dx
x n dx расходится при n 1.
a
(a 0)
e
0
x
сходится, при 0 ,
dx
расходится при 0.

13.

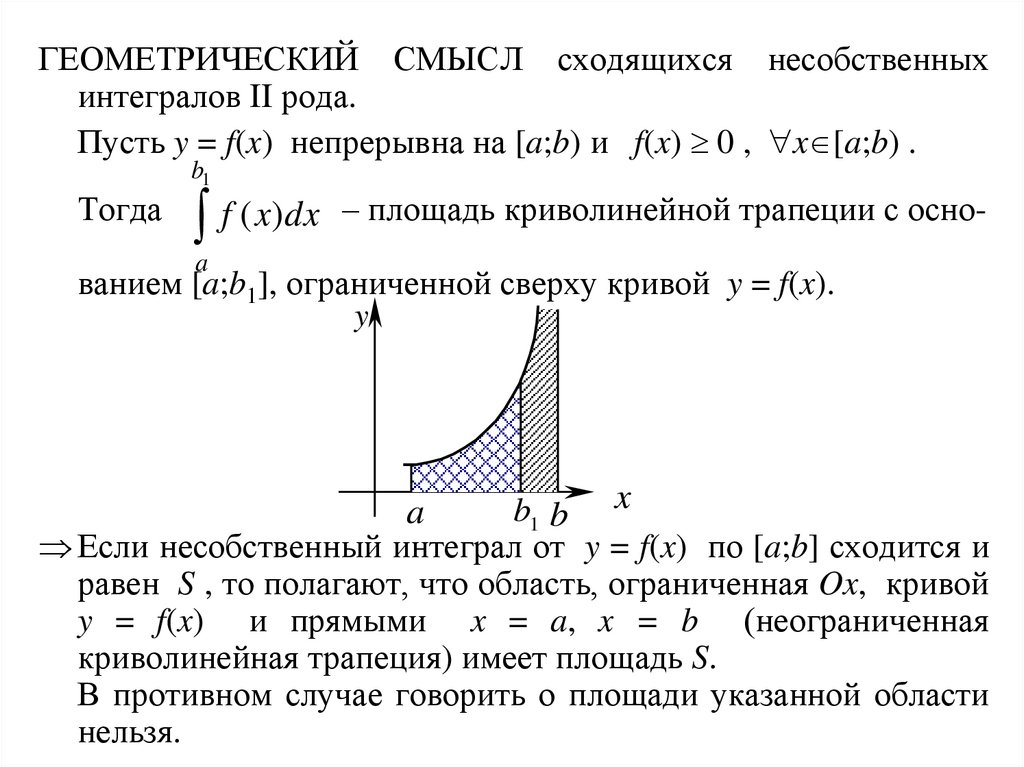
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ сходящихся несобственных
интегралов II рода.
Пусть y = f(x) непрерывна на [a;b) и f(x) 0 , x [a;b) .
b1
Тогда
– площадь криволинейной трапеции с осноf
(
x
)
dx
a
ванием [a;b1], ограниченной сверху кривой y = f(x).
y
b1 b x
a
Если несобственный интеграл от y = f(x) по [a;b] сходится и
равен S , то полагают, что область, ограниченная Ox, кривой
y = f(x) и прямыми x = a, x = b (неограниченная
криволинейная трапеция) имеет площадь S.
В противном случае говорить о площади указанной области
нельзя.