Определенный интеграл. Глава 2

1.

Математический анализ
Глава 2. Определенный интеграл
Лектор Ефремова О.Н.
2025 г.

2.

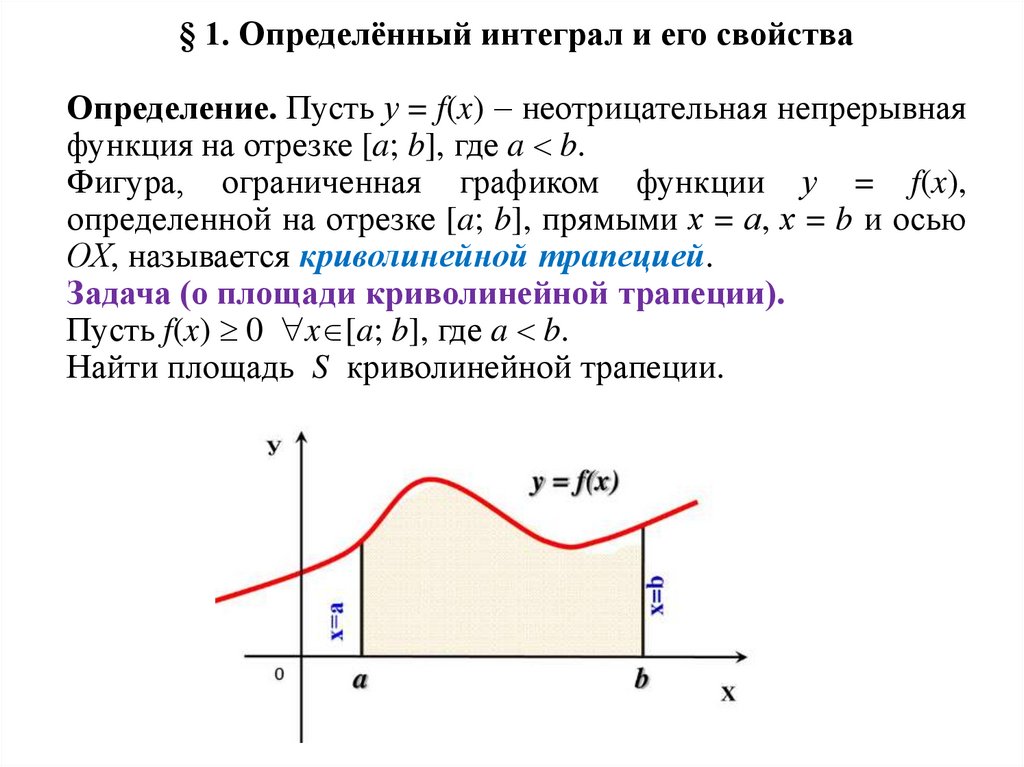
§ 1. Определённый интеграл и его свойства
Определение. Пусть у = f(x) неотрицательная непрерывная
функция на отрезке [a; b], где a b.
Фигура, ограниченная графиком функции у = f(x),
определенной на отрезке [a; b], прямыми х = а, х = b и осью
ОХ, называется криволинейной трапецией.
Задача (о площади криволинейной трапеции).
Пусть f(x) 0 x [a; b], где a b.
Найти площадь S криволинейной трапеции.

3.

Обозначим длину отрезка
[xi – 1; xi ] через xi = xi x i – 1.
На каждом i-том отрезке возьмем
произвольную точку i и
вычислим значение функции в
этой точке. Тогда площадь i-го
прямоугольника можно найти по
формуле Si = xi f( i ).
Площадь ступенчатой фигуры, составленной из
прямоугольников с основаниями xi и высотами f( i ), равна сумме
площадей всех прямоугольников.
Тогда площадь криволинейной трапеции S примерно равна
Пусть
max [ xi 1 ; xi ] . Тогда
1 i n

4. Определенный интеграл: определение и условие его существования

Пусть f(x) задана на отрезке [a; b].
Определение.
1. Разобьем отрезок [a; b] на n частей точками
x0 = a, x1, x2, … , xn = b,
где x0 < x1 < x2 < … < xn.
2. На каждом отрезке [xi–1; xi] (i = 1, 2, … , n) выберем произвольную точку i и найдем произведение
f( i) Δxi,
где Δxi = xi – xi–1 – длина отрезка [xi–1; xi].
n
Сумма
I n ( xi , i )
f ( i ) xi
i 1
называется интегральной суммой для функции f(x) на
отрезке [a; b].

5.

Пусть max [ xi 1 ; xi ] .
1 i n
Определение. Число I называется пределом интегральных
сумм In(xi, i)
при 0, если для любого > 0
существует > 0
такое, что для любого разбиения
отрезка [a; b], у которого < , при любом выборе точек i
выполняется неравенство
| In(xi, i) – I | < .
Определение. Если существует предел интегральных сумм
In(xi, i) при 0, то его называют определенным
интегралом от функции f(x) на отрезке [a; b] и
обозначают
.
Таким образом,

6.

Запись
читают: интеграл a от до b эф от икс дэ, икс.
Называют: [a; b] – промежуток интегрирования,
a и b – нижний и верхний предел интегрирования,
f(x) – подынтегральная функция,
f(x)dx – подынтегральное выражение,
x – переменная интегрирования.

7.

Определение. Функция f(x), для которой на отрезке
[a; b] существует определенный интеграл, называется
интегрируемой на этом отрезке.
Теорема (необходимое условие интегрируемости функции на
[a; b]).
Если функция f(x) интегрируема на отрезке [a; b], то она на
этом отрезке ограничена.
Теорема (достаточное условие интегрируемости функции на
[a; b]).
Для того, чтобы функция f(x) была интегрируема на [a; b],
достаточно чтобы выполнялось одно из условий:
1) f(x) непрерывна на [a; b];
2) f(x) монотонна на [a; b];
3) f(x) ограничена на [a; b] и имеет на [a; b] конечное число
точек разрыва.

8.

Замечание. В определении
полагали, что a < b.
♦ Если a > b , то
.
a
♦ Если a = b , то
определенного
f ( x)dx 0 .
a
интеграла

9. Свойства определенного интеграла

1. Геометрический смысл определенного интеграла.
Если f(x) – непрерывна на [a; b] и f(x) 0, x [a; b], то
b
f ( x)dx S ,
a
где S – площадь криволинейной трапеции с основанием [a; b]
и ограниченной сверху кривой y = f(x).
2. Физический смысл определенного интеграла.
Если функция v = f(t) задает скорость движущейся точки в
момент времени t, то
T2
v(t )dt
T1
определяет путь S, пройденный точкой за промежуток
времени [T1; T2].

10.

3.
4. Постоянный множитель k (k 0) можно выносить за знак
определенного интеграла, т.е.
5. Определенный интеграл от алгебраической суммы двух
(конечного числа) функций равен алгебраической сумме
интегралов от этих функций:

11.

6. Если отрезок интегрирования [a; b] разбит точкой c на две
части [a; c] и [c; b], то
7. Если f(x) > 0 (f(x) 0) x [a; b], то
8. Если f(x) (x) x [a; b], то
.

12.

9. Следствие свойств 8 и 3.
Если m и M – соответственно наименьшее и наибольшее
значения функции f(x) на отрезке [a; b], то
b
m(b a) f ( x)dx M (b a) .
a
a
f ( x)dx 0.
10. Если f(x) – нечётная функция, то
a
Если f(x) – чётная функция, то
a
a
a
0
f ( x)dx 2 f ( x)dx.

13.

11. Теорема о среднем.
Если функция f(x) непрерывна на [a; b], то в интервале (a; b)
найдется такая точка c, что справедливо равенство
.

14. §2. Вычисление определенного интеграла

1. Интеграл с переменным верхним пределом.
Определение. Пусть f(t) интегрируема
на [a; b]. Тогда f(t) интегрируема для
x [a; x], где a x b.
Функция
интегралом с переменным верхним пределом.
называется

15.

Теорема (о производной определенного интеграла по переменному верхнему пределу).
Производная интеграла от непрерывной функции по
переменному верхнему пределу существует и равна значению
подынтегральной функции в точке, равной верхнему пределу,
т.е.
Доказательство.

16.

2. Формула Ньютона-Лейбница
Теорема. Если функция y = f(x) непрерывна на отрезке [a; b] и
функция F(x) какая-либо первообразная для f(x) на [a; b],
то справедлива формула:
b
f (t )dt F (b) F (a) .
a
Доказательство
(1)

17.

Формула (1) называется формулой Ньютона – Лейбница.
Разность F(b) – F(a) принято сокращенно записывать в виде
b
F (b) F (a) F ( x) a .
Используя это обозначение, формулу (1) можно записать
b
в виде
a
b
f ( x)dx F ( x) a F (b) F (a) .

18. 2. Замена переменной в определенном интеграле

Теорема (о замене переменной в определенном интеграле).
Пусть функция f(x) непрерывна на отрезке [a; b].
Пусть функция x = (t) непрерывно дифференцируема на
отрезке [ ; ] и ( ) = а, ( ) = b.
Тогда справедлива формула
.
(2)
Формула (2) называется формулой замены переменной в
определенном интеграле.
Доказательство.

19.

Пример. Вычислить интеграл
Пример. Вычислить интеграл
.
.

20.

3. Формула интегрирование по частям в
определенном интеграле
Теорема 4.
Пусть функции u(x) и v(x) непрерывно дифференцируемы
на [a; b]. Тогда справедливо равенство
b
a
b
b
udv uv a
vdu .
(3)
a
Формула (3) называется формулой интегрирования по
частям в определенном интеграле.
Доказательство.
Пропустить 20 строк

21.

§3. Приложения определенного интеграла
1. Площадь плоской области
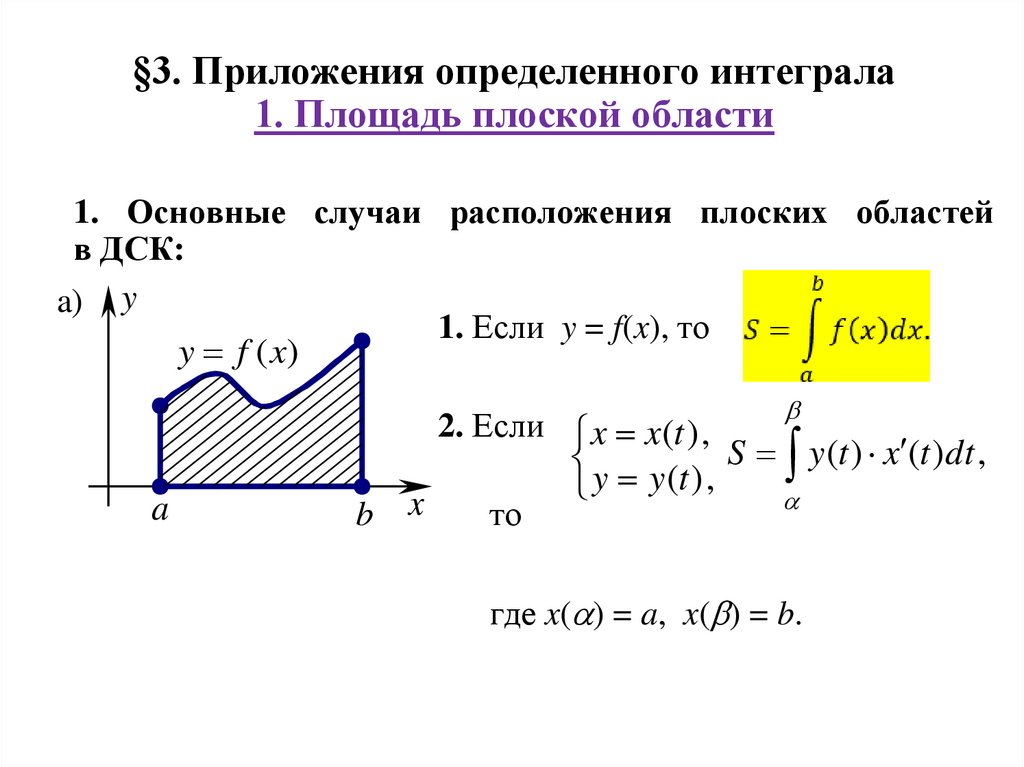
1. Основные случаи расположения плоских областей
в ДСК:
a) y
1. Если y = f(x), то
y f (x)
2. Если x x(t ) ,
S y (t ) x (t )dt ,
a
b
x
то
y y (t ) ,
где x( ) = a, x( ) = b.

22.

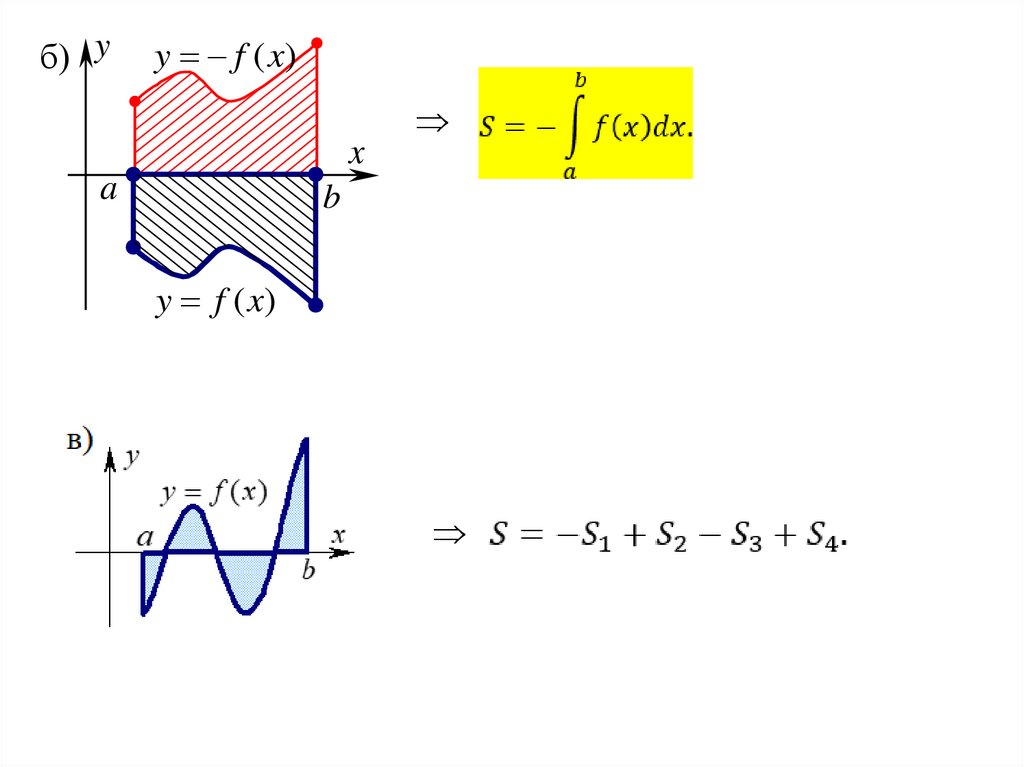
б) y
y f (x)
x
a
b
y f (x)

23.

в)
Пусть область D ограничена
графиками функций y = f1(x),
y = f2(x), прямыми x = a и x = b,
где a < b и f1(x) f2(x) x [a; b].
Тогда площадь области D можно найти по формуле:
Пропустить 20 строк

24. Декартова и полярная система координат

Декартова система координат (ДСК)
y
O – начало координат;
M
Ox, Oy – координатные оси.
y
(x, y) – координаты точки M;
x
x – абсцисса точки M ,
O x
y – ордината точки M .
Полярная система координат (ПСК)
O – полюс; OP – полярная ось.
y
(r, φ) – полярные координаты M .
M
r – полярный радиус точки M ;
r
φ – полярный угол точки M.
x
O
P
Пропустить 10 строк
Cвязь декартовых и полярных
координат:
x = rcosφ, y = rsinφ .

25.

Аналитический способ задания функции
1) у = f (x) (или F (x, y) = 0 )
уравнение функции, заданной явно
(неявно)
2) x = x(t),
y = y(t)
параметрические
уравнения кривой в ДСК
3) r = r (φ) (или ρ = ρ (φ) )
уравнение кривой в ПСК

26.

Аналитический способ задания функции
1) у = f (x) (или F (x, y) = 0 )
уравнение функции, заданной явно
(неявно)
2) x = x(t),
y = y(t)
параметрические
уравнения кривой в ДСК
3) r = r (φ) (или ρ = ρ (φ) )
уравнение кривой в ПСК
Декартов лист

27.

2. Плоская область в полярной системе координат.
Криволинейным сектором называется область, ограниченная двумя лучами = , = и кривой r = r( ), где .
r f ( )
O
x
Площадь криволинейного сектора в ПСК находится по
формуле:
Пропустить 0.5 страницы

28.

Площадь плоской фигуры
Область ограничена
линиями
1) y = f(x), x = a, x = b,
y=0
2) y = f₁(x), y = f₂(x),
x = a, x = b
3) x = x(t), y = y(t),
x(a) = α, x(b) = β
4) r = r(φ), φ₁ = α, φ₂ = β
Формула

29.

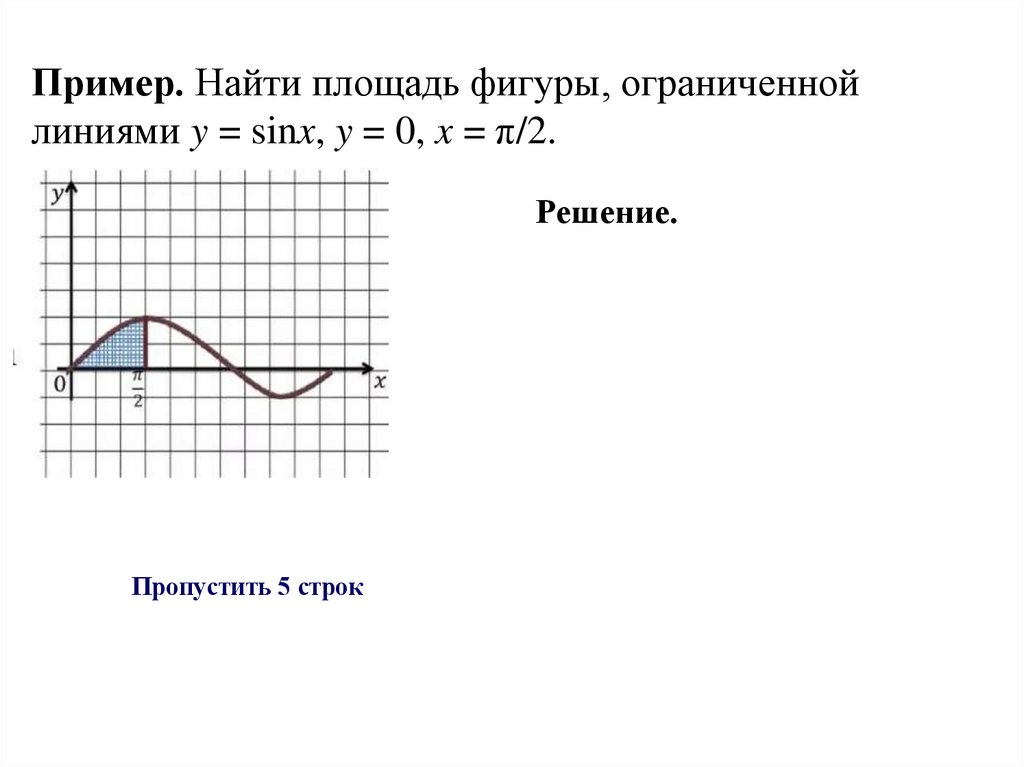
Пример. Найти площадь фигуры, ограниченной
линиями y = sinx, y = 0, x = π/2.
Решение.
Пропустить 5 строк

30.

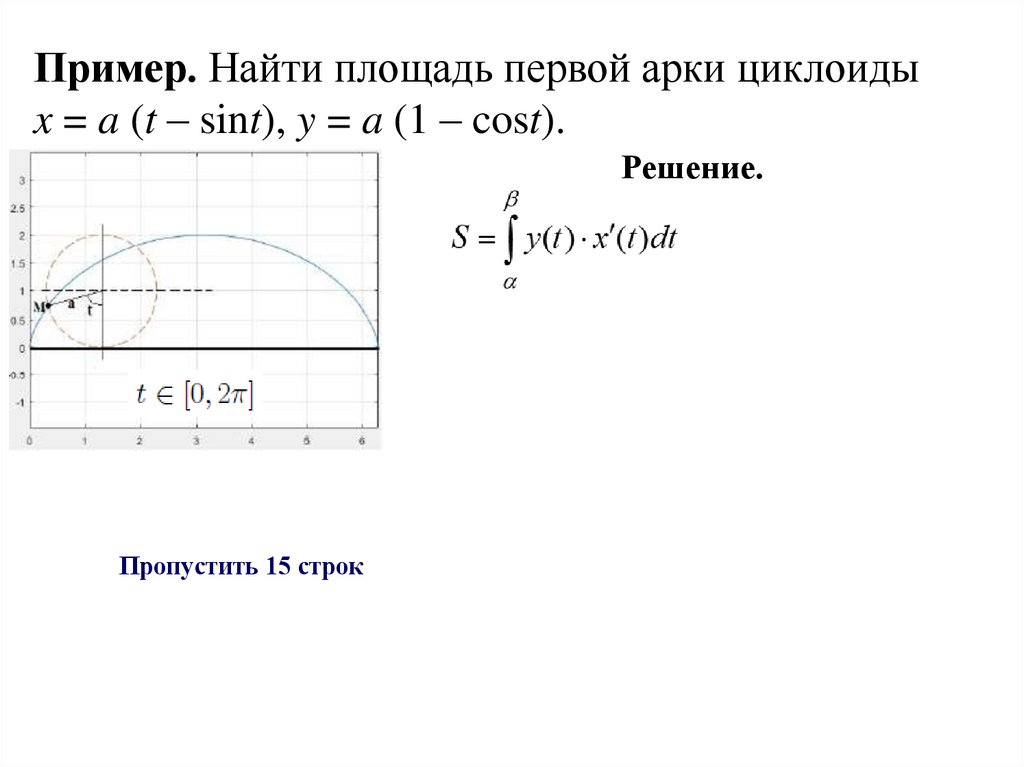
Пример. Найти площадь первой арки циклоиды
x = a (t – sint), y = a (1 – cost).
Решение.
Пропустить 15 строк

31.

Пропустить 20 строк

32. 2. Длина плоской кривой

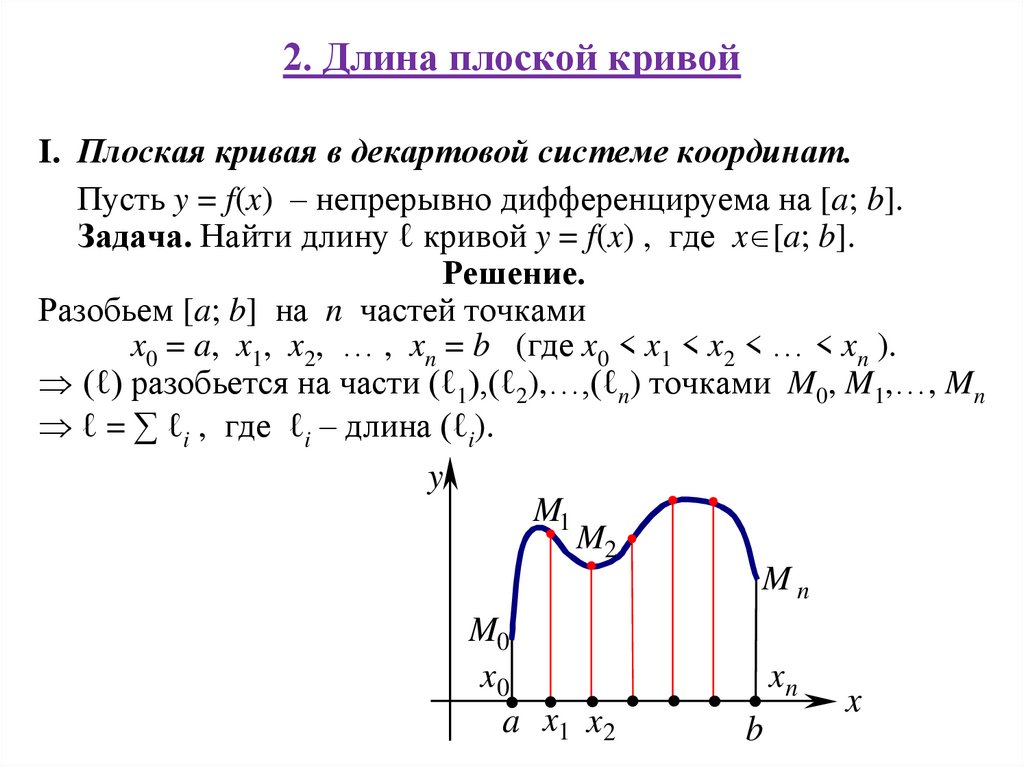
I. Плоская кривая в декартовой системе координат.
Пусть y = f(x) – непрерывно дифференцируема на [a; b].
Задача. Найти длину ℓ кривой y = f(x) , где x [a; b].
Решение.
Разобьем [a; b] на n частей точками
x0 = a, x1, x2, … , xn = b (где x0 < x1 < x2 < … < xn ).
(ℓ) разобьется на части (ℓ1),(ℓ2),…,(ℓn) точками M0, M1,…, Mn
ℓ = ∑ ℓi , где ℓi – длина (ℓi).
y
M1
M2
Mn
M0
x0
xn
x
a x1 x2
b

33.

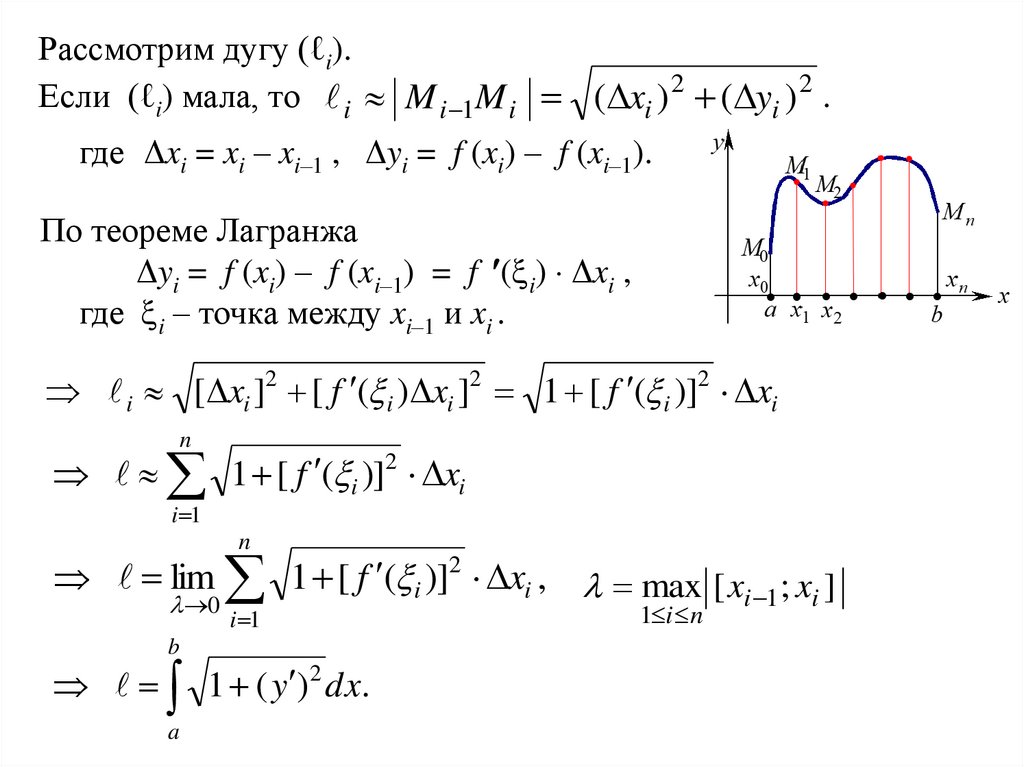
Рассмотрим дугу (ℓi).
Если (ℓi) мала, то i M i 1M i ( xi ) 2 ( yi ) 2 .
где Δxi = xi – xi–1 , Δyi = f (xi) – f (xi–1).
По теореме Лагранжа
Δyi = f (xi) – f (xi–1) = f ( i) Δxi ,
где i – точка между xi–1 и xi .
i [ xi ]2 [ f ( i ) xi ]2 1 [ f ( i )]2 xi
n
1 [ f ( i )]2 xi
i 1
n
lim 1 [ f ( i )]2 xi , max [ xi 1 ; xi ]
0
i 1
b
1 ( y ) 2 dx.
a
1 i n

34.

35.

II. Плоская кривая задана параметрическими уравнениями.
Пусть кривая (ℓ) не имеет самопересечений и задана параметрическими уравнениями: x (t ) ,
y (t ) ( t ) ,
где (t), (t) – непрерывно дифференцируемые на [ ; ].
Тогда
длину
кривой,
заданной
уравнениями [ ; ], находят по формуле
параметрическими
(4)

36.

37.

III. Плоская кривая задана в полярных координатах.
Пусть r = r( ) – непрерывно дифференцируема на [ ; ].
Задача. Найти длину кривой r = r( ), где [ ; ].
Решение.

38.

39.

Длина плоской кривой
1) пусть y = f(x) на
[a, b]
2) x = x(t), y = y(t)
на [ , ]
3) r = r(φ) на [ , ]
r 2 (r ) 2 d .

40.

Пример. Найти длину дуги кривой r = 1 + cosφ,
где 0 ≤ φ ≤ π/6.
Решение.
r 2 (r ) 2 d .
кардиоида
Пропустить 5 строк

41. 3. Вычисление объема тела

I. По площадям параллельных сечений.
Пусть (V) – замкнутое и ограниченная область в Oxyz (тело).
Пусть S(x) (a x b) – площадь любого сечения тела
плоскостью, перпендикулярной оси Ox.
b
Тогда объем тела (V) находят по формуле
V S ( x)dx.
a

42.

Доказательство.
1. Разобьем [a; b] на n частей точками
x0 = a , x1 , x2 , … , xn = b (где x0 < x1 < x2 < … < xn ).
Плоскости x = x0, x = x1, x = x2, … , x = xn разобьют (V) на
части (V1), (V2), … , (Vn).
Тогда V = ∑ Vi , где Vi – объем (Vi).
2. Рассмотрим (Vi).
xi 1
xi
x

43.

II. Объем тела вращения.
Пусть (V) – тело, которое получается в результате вращения
вокруг Ox криволинейной трапеции с основанием [a; b],
ограниченной y = f(x). y
B
A
y f ( x)
x
a
b
b
2
V
[
f
(
x
)]
dx.
Объем этого тела находят по формуле: x
a
Пропустить 15 строк

44. 4. Физические приложения определенного интеграла

1. Пройденный путь.
Пусть точка движется вдоль некоторой кривой со скоростью v(t)
Тогда путь S, пройденный точкой за время [T1; T2], равен
T2
S v(t )dt .
T1
2. Масса отрезка.
Пусть (x) – плотность распределения массы на отрезке [a; b].
b
Тогда масса отрезка равна
m ( x)dx.
a
3. Работа переменной силы.
Пусть под действием силы F̄ тело движется вдоль оси Ox из
точки x1 = a в точку x2 = b.
b
Если F = F(x) и F̄⇈Ox, то работа силы равна A F ( x)dx.
a

45. §4. Несобственные интегралы

Для существования
необходимы условия:
1) отрезок [a; b] – конечен,
2) функция f(x) – ограничена.
Несобственные интегралы – это обобщение понятия
определенного интеграла на случай, когда одно из этих условий
не выполняется.

46. 1. Несобственные интегралы I рода (по бесконечному промежутку)

Пусть y = f(x) непрерывна на [a; + ).
Тогда y = f(x) непрерывна на [a; b], где b a.
b
Следовательно, существует
b
Пусть
f ( x)dx.
a
f ( x)dx I (b) , D(I) = [a;+ ).
a
Определение. Несобственным интегралом I рода от функции
f(x) по промежутку [a; + ) называется предел функции I(b) при b + .
Обозначают:

47.

Таким образом, по определению
b
f ( x)dx b lim I (b) b lim f ( x)dx .
a
(5)
a
При этом, если предел в правой части формулы (5) существует
и конечен, то несобственный интеграл называют
сходящимся.
Если предел в правой части формулы (5) не существует или
равен бесконечности, то несобственный интеграл называют
расходящимся.
Если y = f(x) непрерывна на (– ; b], то аналогично определяется и обозначается несобственный интеграл I рода для
функции f(x) по промежутку (– ; b]:
b
b
a
f ( x)dx .
f ( x)dx alim

48.

Если y = f(x) непрерывна на ℝ, то несобственным интегралом
I рода для функции f(x) по промежутку (– ; + )
называют интеграл
c
f ( x)dx f ( x)dx f ( x)dx ,
(6)
c
где c – любое число.
Несобственный интеграл от f(x) по промежутку (– ; + )
называется сходящимся, если ОБА интеграла в правой части
формулы (6) сходятся.
В противном случае, несобственный интеграл по промежутку
(– ; + ) называется расходящимся.
Пропустить 15 строк

49.

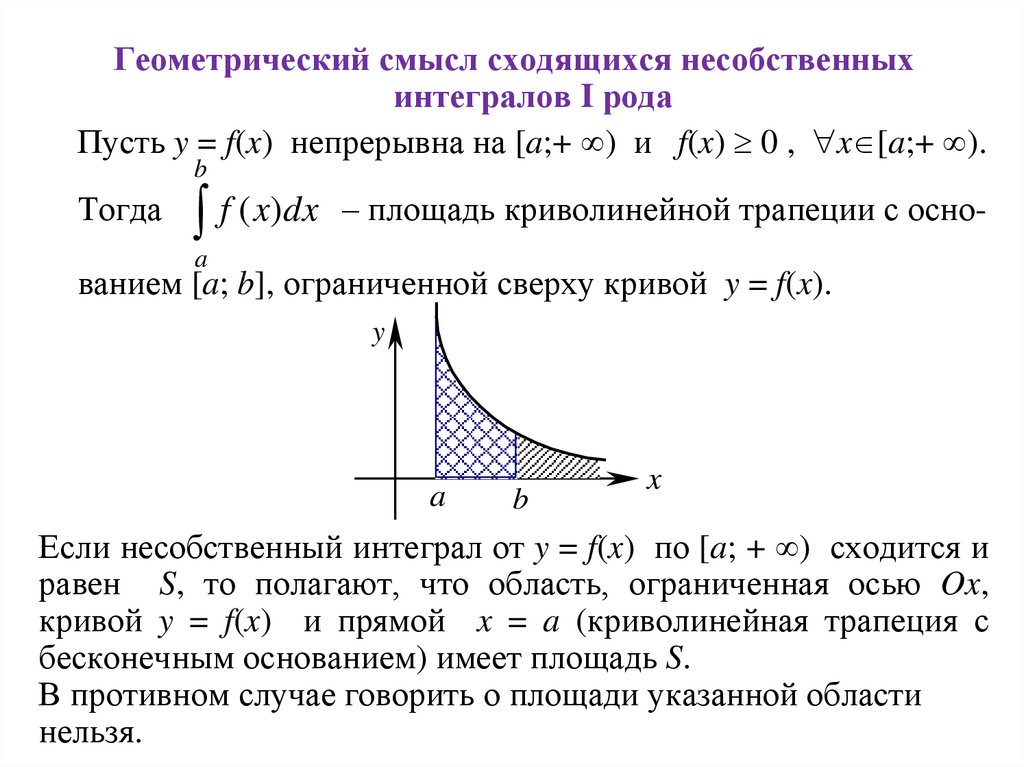
Геометрический смысл сходящихся несобственных
интегралов I рода
Пусть y = f(x) непрерывна на [a;+ ) и f(x) 0 , x [a;+ ).
b
Тогда
f ( x)dx – площадь криволинейной трапеции с осноa
ванием [a; b], ограниченной сверху кривой y = f(x).
y
a
b
x
Если несобственный интеграл от y = f(x) по [a; + ) сходится и
равен S, то полагают, что область, ограниченная осью Ox,
кривой y = f(x) и прямой x = a (криволинейная трапеция с
бесконечным основанием) имеет площадь S.
В противном случае говорить о площади указанной области
нельзя.

50.

У несобственных интегралов I рода сохраняются некоторые
свойства определенных интегралов (свойства 4, 5, 6, 7, 8).
Кроме того, для несобственных интегралов существует
обобщение формулы Ньютона – Лейбница.
Пусть F(x) – первообразная для f(x) на [a; + ).
Тогда b [a; + ) имеем
b
lim f ( x)dx lim F (b) F (a)
b
a
b
f ( x)dx b lim F (b) F (a)
a
(7)

51.

Обозначим
lim F (b) F (a) F ( x) a .
b
Тогда (7) примет вид:
f ( x)dx F ( x) a lim F ( x) F (a) .
a
x
(8)
Формулу (8) называют обобщением формулы Ньютона –
Лейбница для несобственных интегралов по промежутку
[a; + ).
Аналогично для несобственных интегралов по промежутку
(– ; b] доказывается справедливость формулы
b
b
f ( x)dx F ( x) F (b) lim F ( x) .
x

52. 2. Признаки сходимости несобственных интегралов I рода

Теорема 1 (первый признак сравнения).
Пусть f(x) и (x) непрерывны на [a; + ) и
0 f(x) (x) , x [c; + ) (где c a).
Тогда:
1) если
( x)dx – сходится, то f ( x)dx тоже сходится,
a
причем
2) если
ходится.
c
c
a
f ( x)dx ( x)dx ;
– расходится, то
тоже рас-

53.

Теорема 2 (второй признак сравнения)
Пусть f(x) и (x) непрерывны и неотрицательны на
[a; + ).
f ( x)
h , где h – действительное число, отличное
x ( x)
Если lim
от нуля, то интегралы
и
ведут себя одинаково относительно сходимости.

54.

Замечания.
1. Теорема 2 остается справедливой и в том случае, если f(x) и
(x) непрерывны и СОХРАНЯЮТ ЗНАК на [a; + ).
2. При использовании теорем 1 и 2 в качестве «эталонных»
интегралов обычно используют следующие несобственные
интегралы:
dx
x n dx
a
(a 0)
x
e
dx
0
Пропустить 15 строк
Пример. Исследовать на сходимость интегралы.
1)
1
dx
1 x 1 x2
3
;
xdx
2)
;
1 x
0
3) e
x2
dx .

55. 3. Несобственные интегралы II рода (от неограниченных функций)

Пусть y = f(x) непрерывна на [a; b) и lim
x b 0
f ( x ) ( )
y = f(x) непрерывна на [a; b1], где a b1 < b.
b1
существует
a
b1
Имеем:
f ( x)dx .
f ( x)dx I (b1) , D(I) = [a; b).
a
Определение. Несобственным интегралом II рода по
промежутку [a; b] от функции f(x), неограниченной в точке
b, называется предел функции I(b1) при b1 b – 0.
b
Обозначают:
f ( x)dx.
a

56.

Таким образом, по определению
b1
b
I (b1 ) lim f ( x)dx .
f ( x)dx b lim
b 0
b b 0
a
1
1
(9)
a
При этом, если предел в правой части формулы (9) существует
и конечен, то несобственный интеграл называют
сходящимся.
В противном случае (т.е. если предел не существует или равен
бесконечности)
несобственный
интеграл
называют
расходящимся.
Если y = f(x) непрерывна на (a; b] и lim
x a 0
f ( x ) ( ) ,
то аналогично определяется и обозначается несобственный
интеграл II рода по промежутку [a; b] от функции f(x),
неограниченной в точке a:
b
b
f ( x)dx a lima 0 f ( x)dx.
a
1
a1

57.

Если y = f(x) непрерывна на [a;b]\{c} и x = c – точка бесконечного разрыва функции, то несобственным интегралом
II рода от функции f(x) по промежутку [a;b] называют
b
c
b
f ( x)dx f ( x)dx f ( x)dx.
a
a
(10)
c
Несобственный интеграл по промежутку [a; b] от функции f(x),
неограниченной внутри этого отрезка, называется сходящимся, если ОБА интеграла в правой части формулы (10)
сходятся.
В противном случае, несобственный интеграл по промежутку
[a; b] называется расходящимся.
Будем рассматривать несобственные интегралы II рода по
промежутку [a; b] от функции, неограниченной в точке b. Для
других несобственных интегралов II рода все полученные
результаты останутся справедливы.

58.

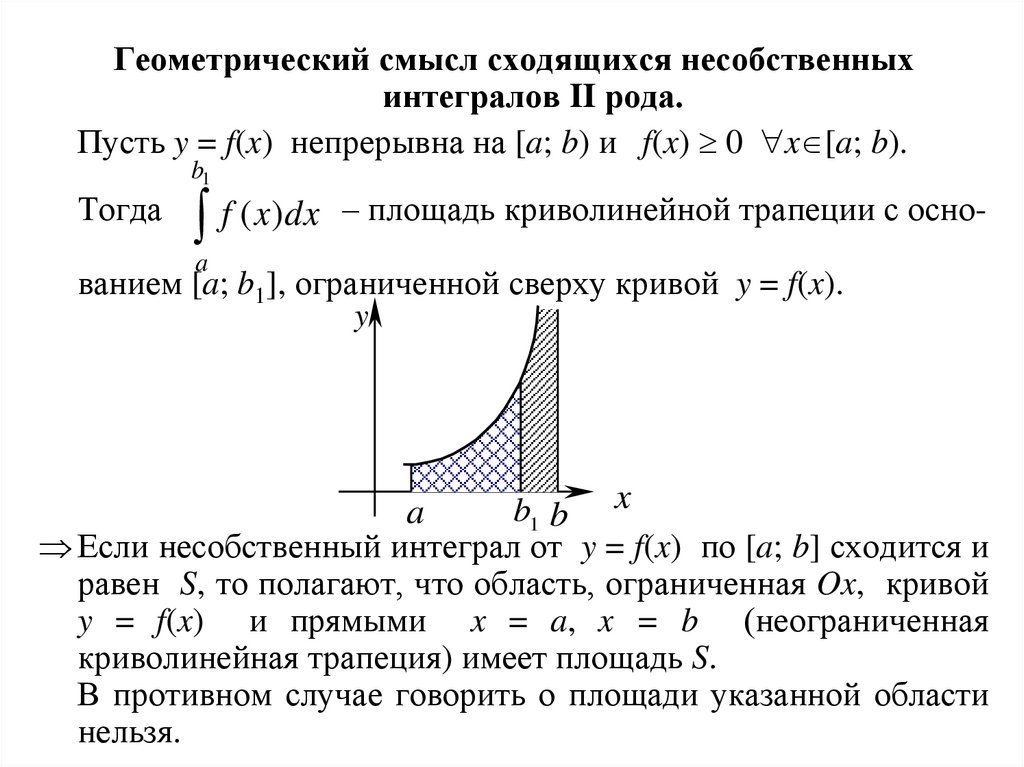
Геометрический смысл сходящихся несобственных
интегралов II рода.
Пусть y = f(x) непрерывна на [a; b) и f(x) 0 x [a; b).
b1
Тогда
– площадь криволинейной трапеции с осноf
(
x
)
dx
a
ванием [a; b1], ограниченной сверху кривой y = f(x).
y
b1 b x
a
Если несобственный интеграл от y = f(x) по [a; b] сходится и
равен S, то полагают, что область, ограниченная Ox, кривой
y = f(x) и прямыми x = a, x = b (неограниченная
криволинейная трапеция) имеет площадь S.
В противном случае говорить о площади указанной области
нельзя.

59.

У несобственных интегралов II рода сохраняются некоторые
свойства определенных интегралов (свойства 4, 5, 6, 7, 8).
Кроме того, для несобственных интегралов II рода также
существует обобщение формулы Ньютона – Лейбница.
Пусть F(x) – первообразная для f(x) на [a; b).
Тогда b1 [a; b) имеем
b1
1
f
(
x
)
dx
F
(
x
)
F (b1 ) F (a)
a
b
a
b1
f ( x)dx lim F (b1 ) F (a)
b b 0
b b 0
lim
1
b
1
a
f ( x)dx b limb 0 F (b1) F (a)
a
1
Пропустить 15 строк
(11)

60.

Ранее вводили обозначение
F (b 0) lim F (b1 ).
b1 b 0
b 0
lim F (b1 ) F (a) F (b 0) F (a) F ( x) a
b1 b 0
.
Тогда (11) примет вид:
b
a
b 0
f ( x)dx F ( x) a lim F ( x) F (a) .
x b 0
(12)
Формулу (12) называют обобщением формулы Ньютона –
Лейбница
для несобственных интегралов II рода от
функций, неограниченных в точке b.
Аналогично для несобственных интегралов II рода от функций,
неограниченных в точке a, доказывается справедливость
формулы
b
a
b
f ( x)dx F ( x) a 0 F (b) lim F ( x) .
x a 0