Геометрия (средняя линия треугольника)

1. Урок геометрии

8 класс

2.

Устная работа
1. Дан ∆ АВС, прямая XY параллельна
прямой AC.
Доказать, что угол 1 равен углу 2.
В
Х 1
А
2
Y
С

3.

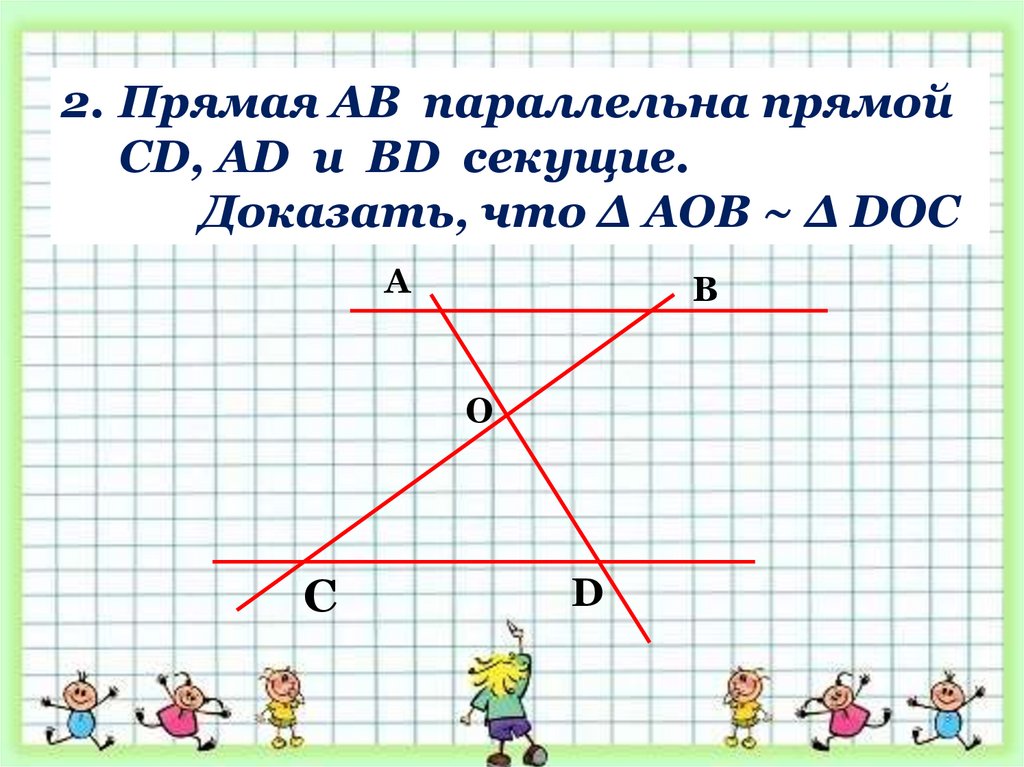
2. Прямая АВ параллельна прямой
CD, AD и BD секущие.
Доказать, что ∆ АОВ ~ ∆ DOС
A
B
O
C
D

4.

Тема урока:
Средняя линия
треугольника

5.

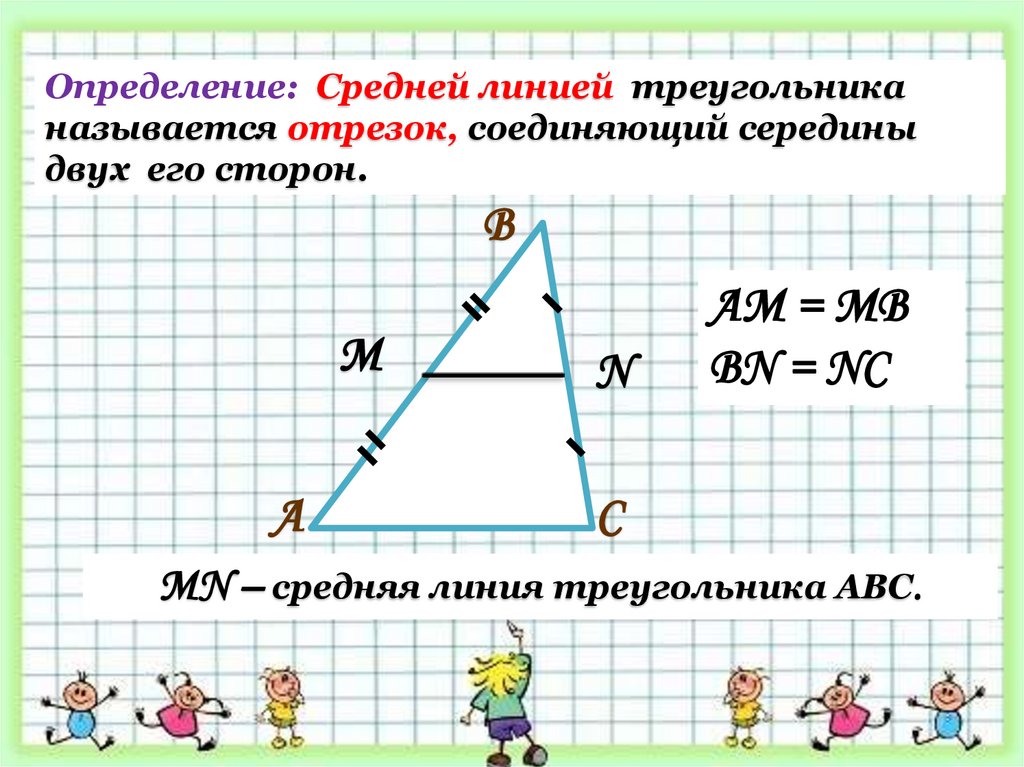
Определение: Средней линией треугольника
называется отрезок, соединяющий середины
двух его сторон.
В
М
А
N
AM = MB
BN = NC
С
МN – средняя линия треугольника АВС.

6. На каком рисунке изображена средняя линия треугольника ?

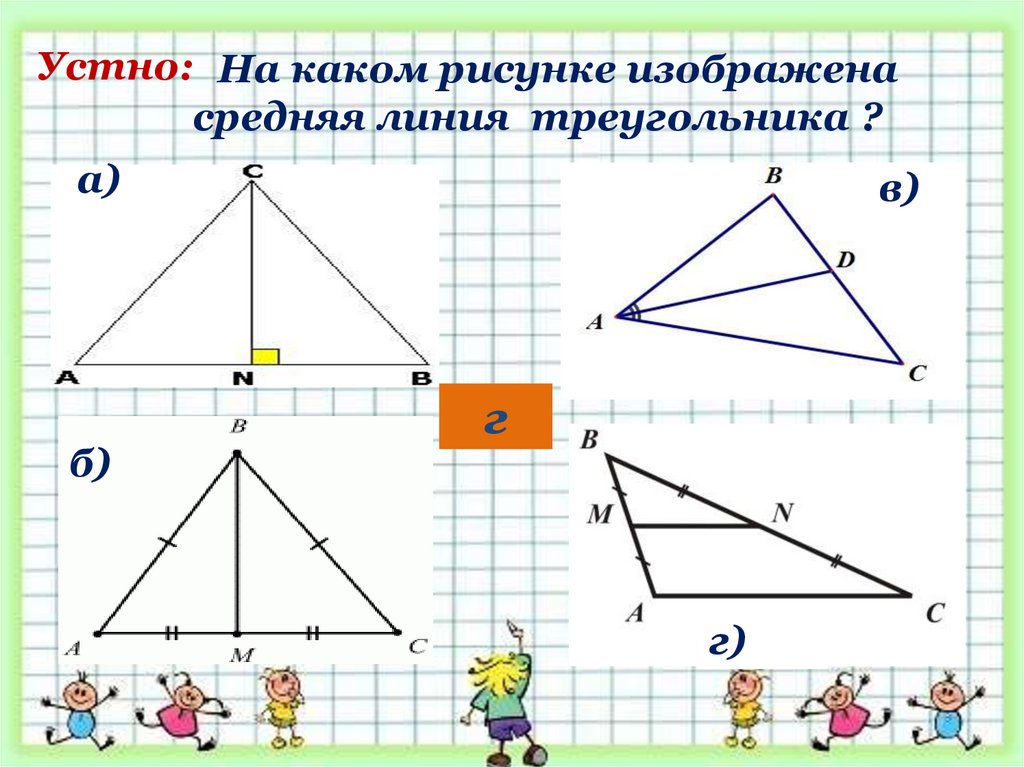
Устно: На каком рисунке изображена
средняя линия треугольника ?
а)
б)
в)
г
г)

7.

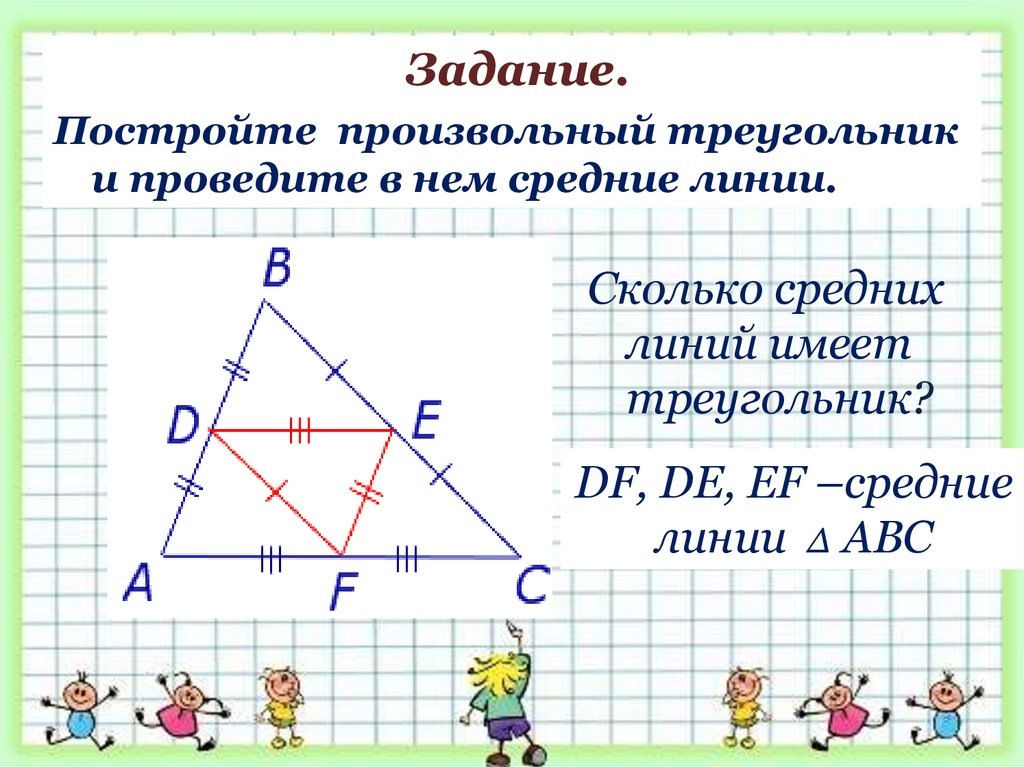
Задание.
Постройте произвольный треугольник
и проведите в нем средние линии.
Сколько средних
линий имеет
треугольник?
DF, DE, EF –средние
линии ∆ АВС

8.

Теорема: Средняя линия треугольника
параллельна одной из его сторон и равна
половине этой стороны.
Дано: ΔАВС, МN – средняя линия.
В
М
А
Доказать: МN || АС, МN =½ АС
Доказательство:
1. ΔАВС ~ ΔВМN,
т.к. ВМ:ВА = ВN:ВС=1:2
и угол В – общий.
N
2. Угол ВМN равен углу ВАС,
а они соответственные при
прямых МN и АС и секущей АВ.
Значит, МN || АС.
С
3. Т.к. ВМ:ВА =1:2,
то и МN:АС=1:2.

9.

Устно:
1. Сколько треугольников вы видите?
∆ADF, ∆ DBE, ∆ ECF,
∆ DEF, ∆ ABC
2. Есть ли равные
треугольники? Почему?
∆ADF= ∆ DBE= ∆ ECF= ∆ DEF
3. Сколько параллелограммов на рисунке?
ADEF, DBEF, ECFD

10.

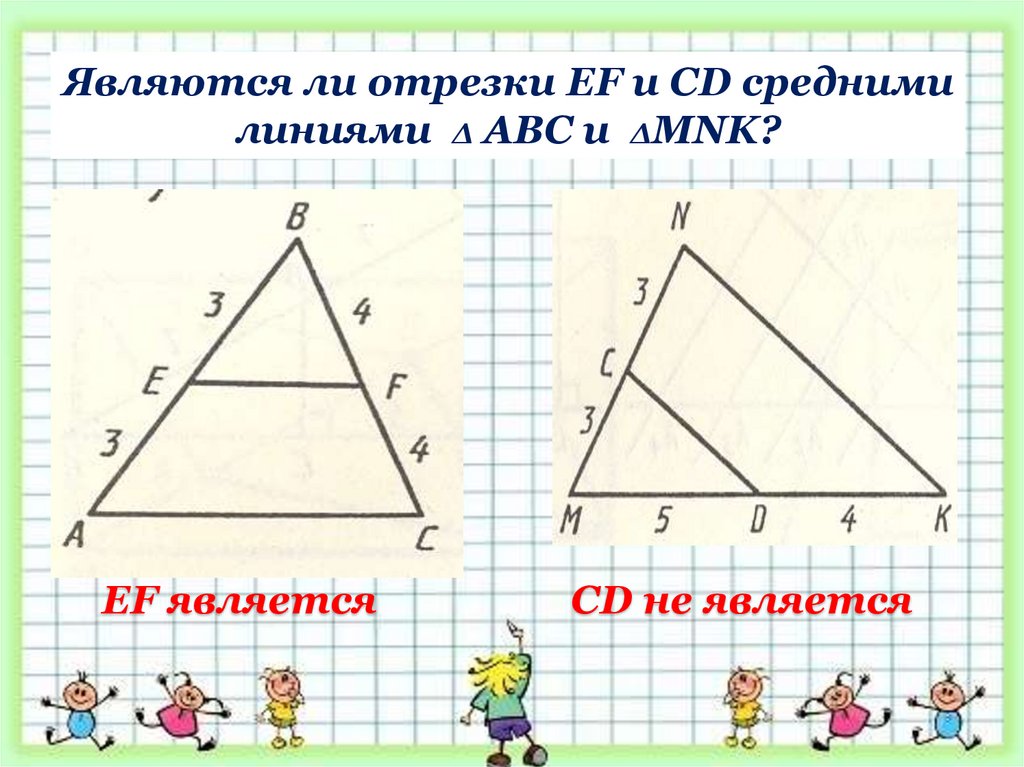
Являются ли отрезки EF и CD средними
линиями ∆ АВС и ∆MNK?
EF является
CD не является

11. Отрезок MN является средней линией треугольника …

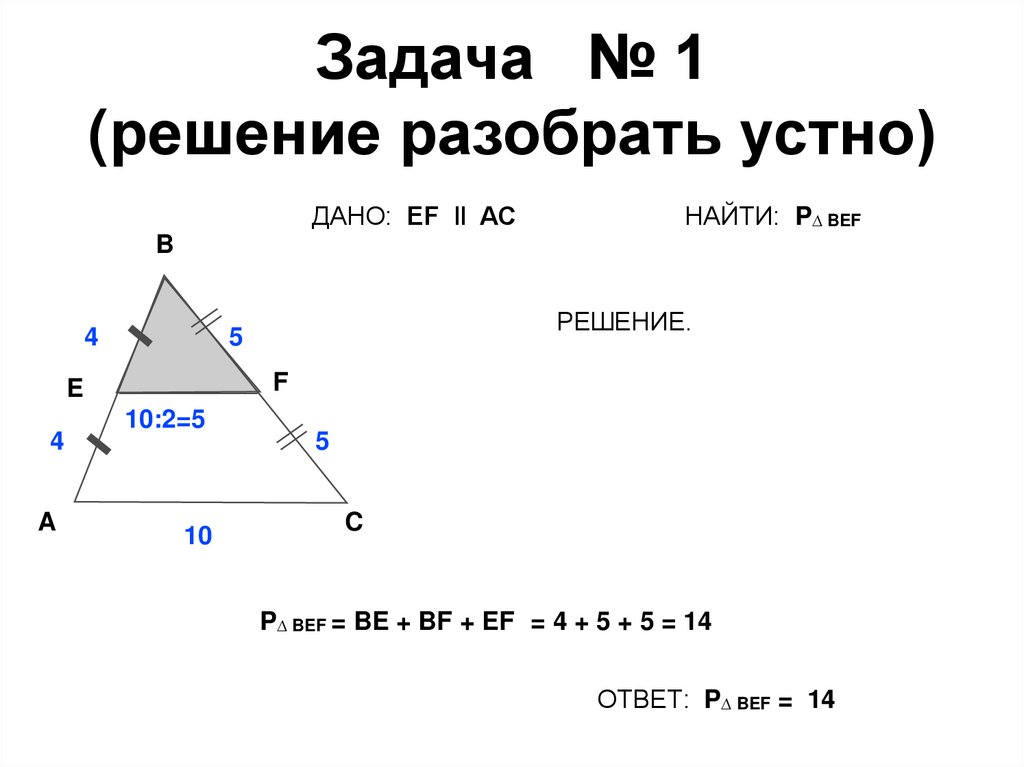
в)

12. Задача № 1 (решение разобрать устно)

ДАНО: EF ‖ AC
НАЙТИ: P∆ BEF
B
4
F
E
4
A
РЕШЕНИЕ.
5
10:2=5
10
5
C
P∆ BEF = BE + BF + EF = 4 + 5 + 5 = 14
ОТВЕТ: P∆ BEF = 14

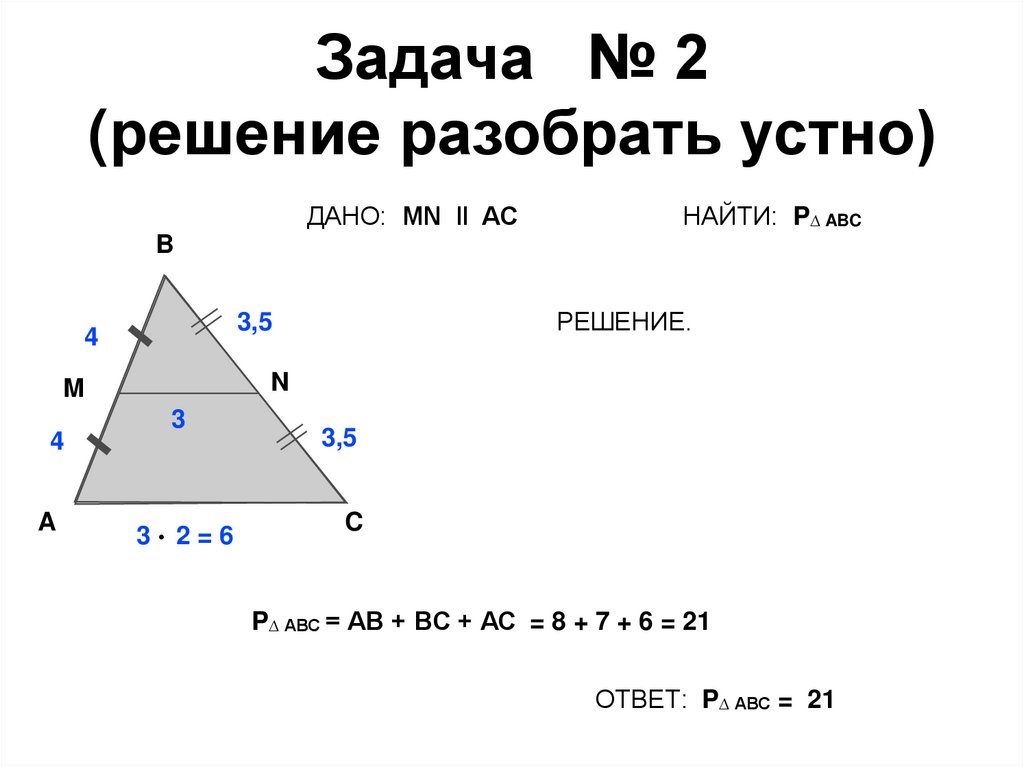
13. Задача № 2 (решение разобрать устно)

ДАНО: MN ‖ AC
НАЙТИ: P∆ ABC
B
N
M
4
A
РЕШЕНИЕ.
3,5
4
3
3• 2=6
3,5
C
P∆ АВС = АВ + BС + АС = 8 + 7 + 6 = 21
ОТВЕТ: P∆ АВС = 21

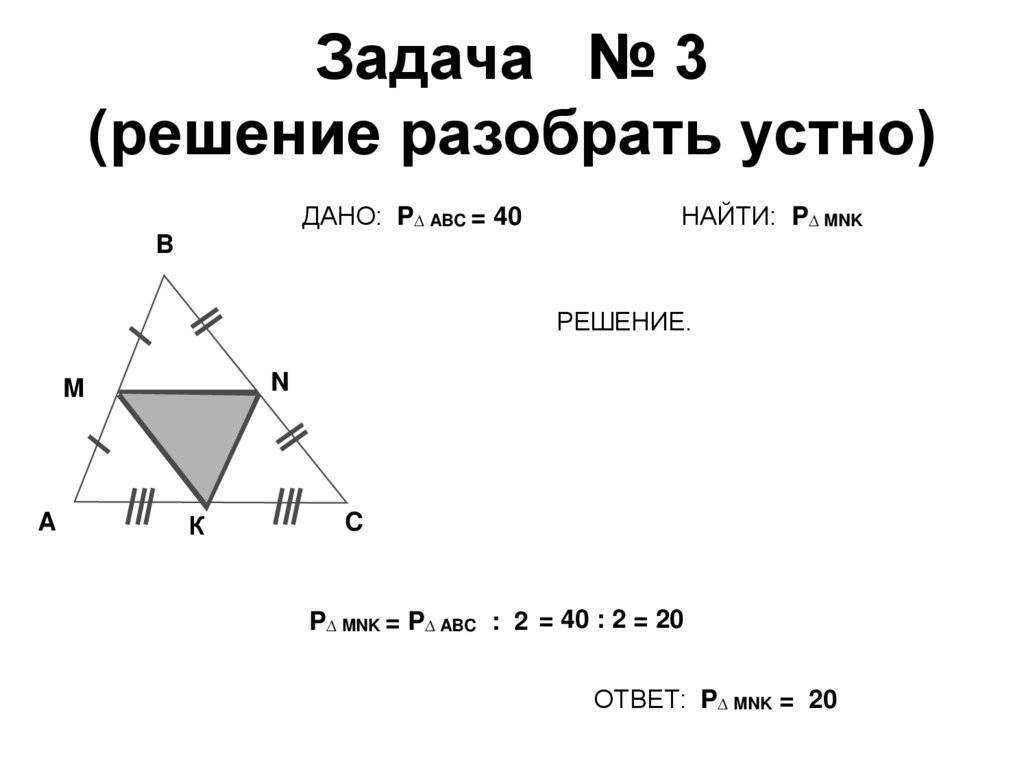
14. Задача № 3 (решение разобрать устно)

ДАНО: P∆ ABC = 40
НАЙТИ: P∆ MNK
B
РЕШЕНИЕ.
N
M
A
К
C
P∆ MNK = P∆ ABC : 2 = 40 : 2 = 20
ОТВЕТ: P∆ MNK = 20

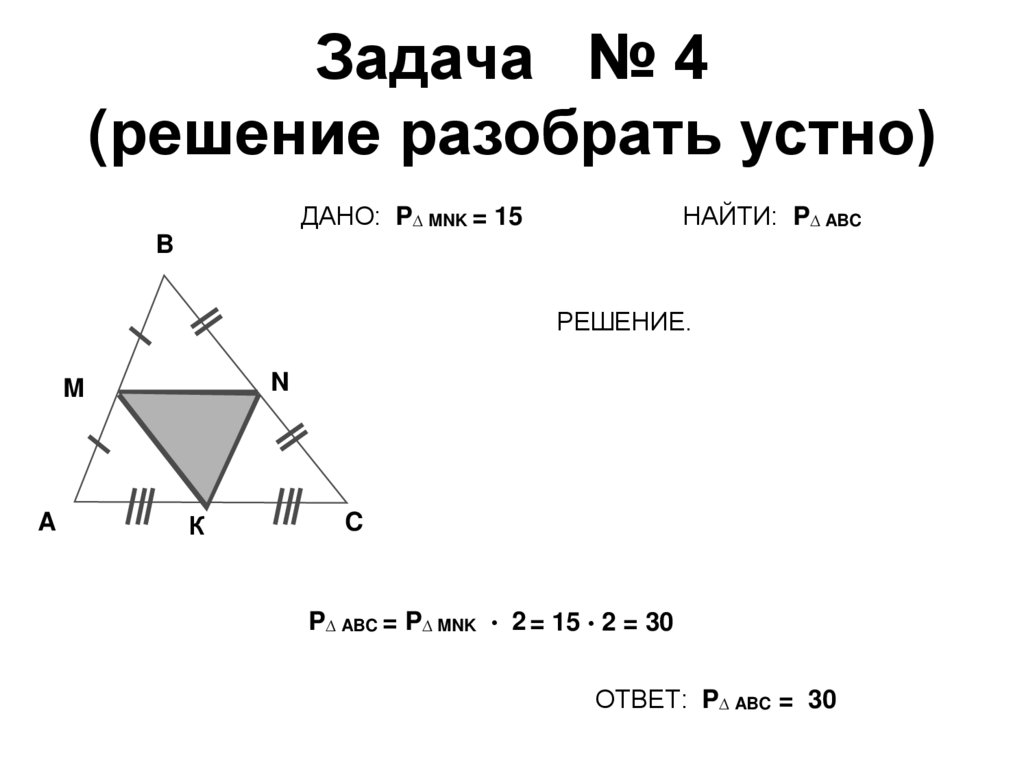
15. Задача № 4 (решение разобрать устно)

ДАНО: P∆ MNK = 15
НАЙТИ: P∆ ABC
B
РЕШЕНИЕ.
N
M
A
К
C
P∆ ABC = P∆ MNK • 2 = 15 • 2 = 30
ОТВЕТ: P∆ ABC = 30

16.

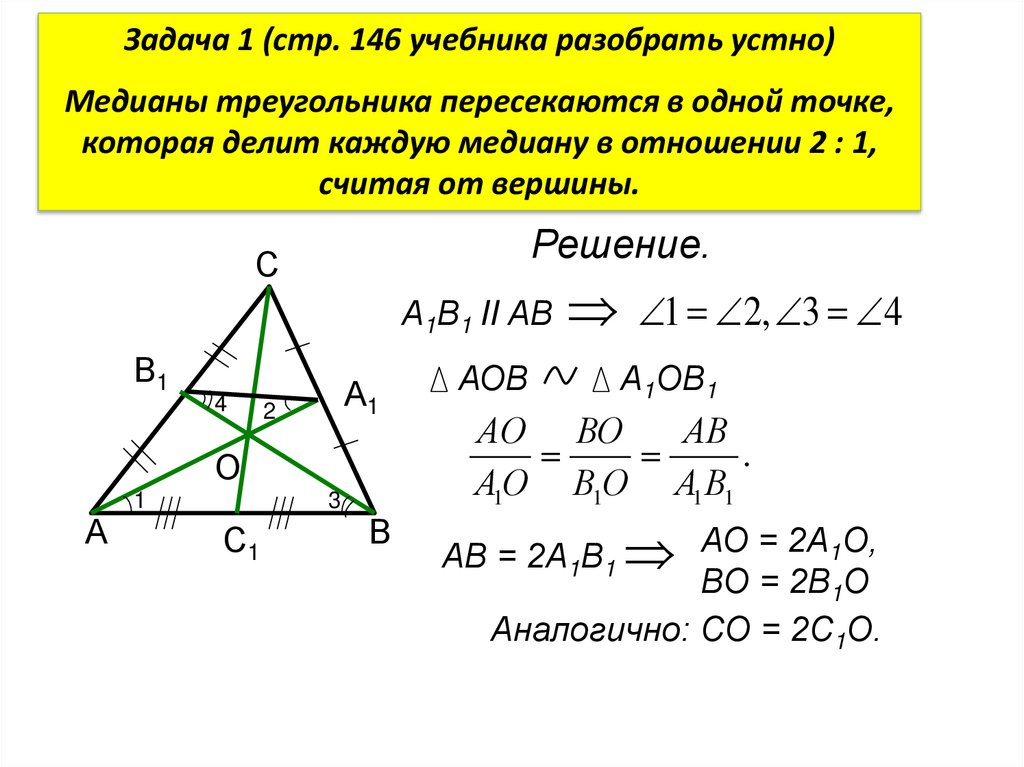
Задача 1 (стр. 146 учебника разобрать устно)
Медианы треугольника пересекаются в одной точке,
которая делит каждую медиану в отношении 2 : 1,
считая от вершины.
Решение.
С
В1
4
А1В1 II АВ 1 2, 3 4
А1
2
О
А
1
3
С1
В
АОВ
А1ОВ1
АО ВО
АВ
.
А1О В1О А1 В1
АВ = 2А1В1 АО = 2А1О,
ВО = 2В1О
Аналогично: СО = 2С1О.

17.

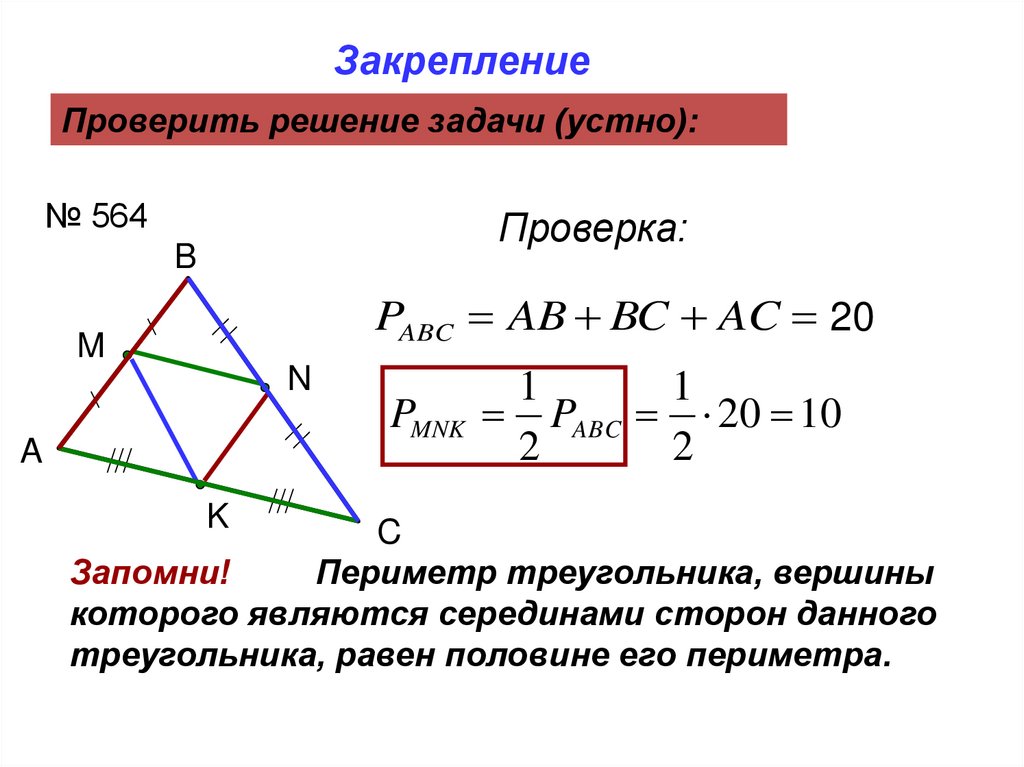
Закрепление
Проверить решение задачи (устно):
№ 564
Проверка:
B
PABC AB BC AC 20
M
N
A
K
1
1
PMNK PABC 20 10
2
2
C
Запомни!
Периметр треугольника, вершины
которого являются серединами сторон данного
треугольника, равен половине его периметра.

18.

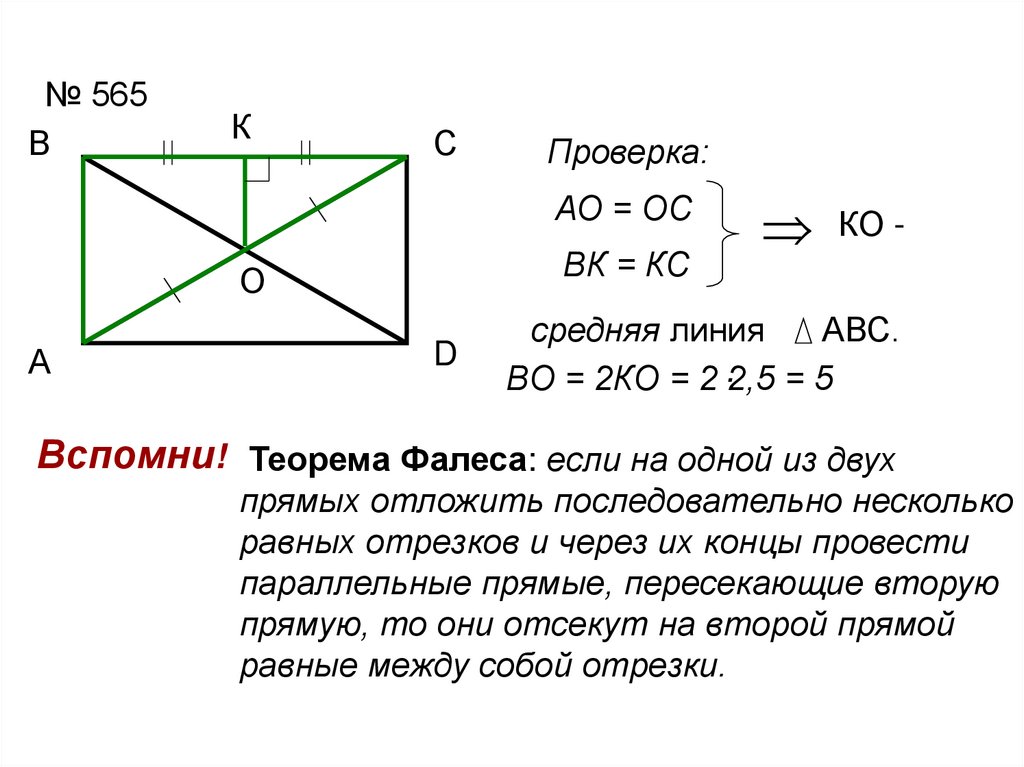
№ 565
В
К
С
Проверка:
АО = ОС
ВК = КС
О
А
D
КО -
средняя линия
АВС.
ВО = 2КО = 2 .2,5 = 5
Вспомни! Теорема Фалеса: если на одной из двух
прямых отложить последовательно несколько
равных отрезков и через их концы провести
параллельные прямые, пересекающие вторую
прямую, то они отсекут на второй прямой
равные между собой отрезки.

19.

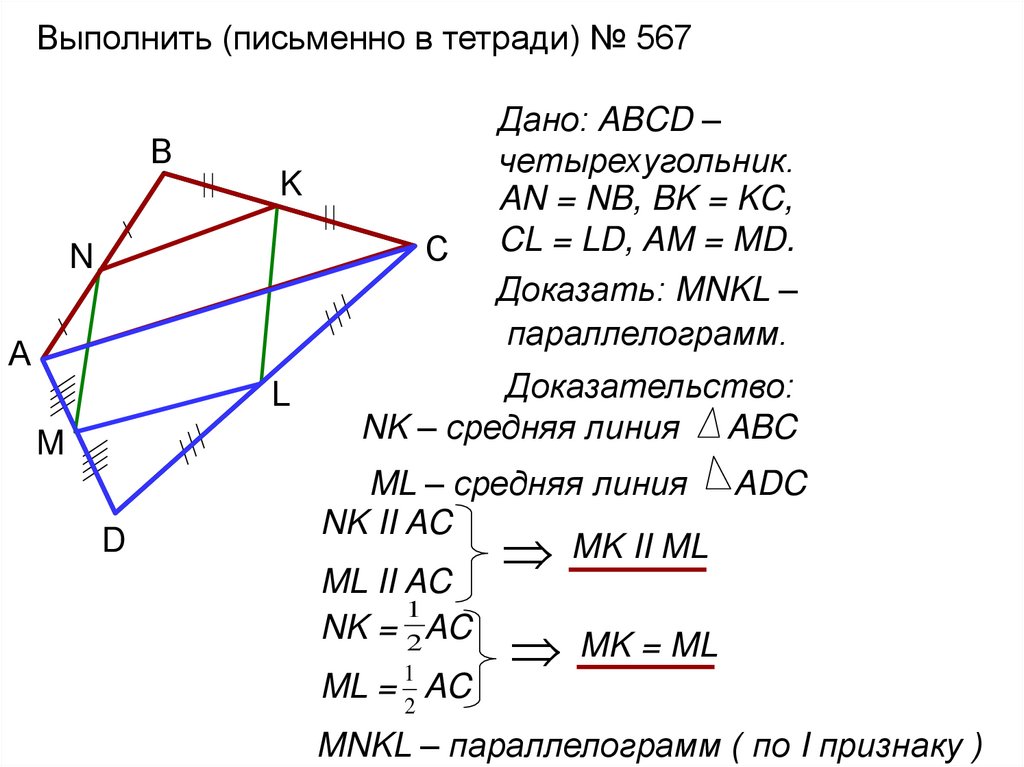
Выполнить (письменно в тетради) № 567
В
K
С
N
А
L
M
D
Дано: ABCD –
четырехугольник.
AN = NB, BK = KC,
CL = LD, AM = MD.
Доказать: MNKL –
параллелограмм.
Доказательство:
NK – средняя линия ABC
ML – средняя линия ADC
NK II AC
MK II ML
ML II AC
1
NK = 2 AC
MK = ML
1
ML = 2 AC
MNKL – параллелограмм ( по I признаку )

20.

Ответить на вопросы устно!
Какую часть от площади ∆АВС составляет
площадь каждого из треугольников?
B
1
4
N
M
A
C
K
Какую часть от периметра ∆АВС составляет
периметр каждого из треугольников? 1
2

21.

Итог урока (выучить!)
1.
Отрезок, соединяющий середины двух сторон
треугольника, называется средней линией
треугольника.
2.
Теорема: Средняя линия треугольника
параллельна одной из его сторон и равна
половине этой стороны.
3.
Медианы треугольника пересекаются в одной точке,
которая делит каждую медиану в отношении 2 : 1,
считая от вершины.