fcb3cd44cdc1449a9596e3cab716543a

1.

2.

Билет 1
1. Сформулируйте определение выпуклого многоугольника
(периметр, диагональ). Сформулируйте теорему о сумме
углов выпуклого многоугольника. Четырехугольник.
2. Точки M и N являются серединами сторон AB и BC
треугольника ABC соответственно. Отрезки AN и CM
пересекаются в точке O, AN=24, CM=15. Найдите AO.
3. В окружность вписан треугольник ABC так, что АВ диаметр окружности. Найдите углы треугольника, если
дуга ВС=134°.
4. В равнобедренной трапеции основания равны 4 и 8, а
один из углов между боковой стороной и основанием
равен 45°. Найдите площадь трапеции.

3.

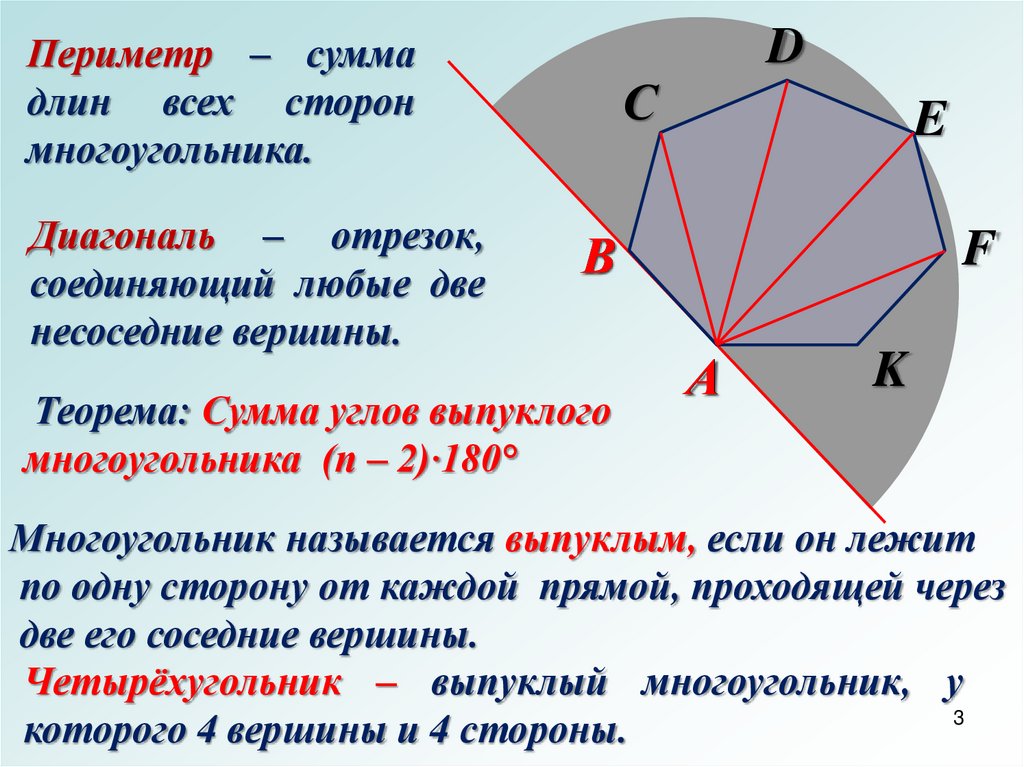
Периметр – сумма
длин всех сторон
многоугольника.
Диагональ – отрезок,
соединяющий любые две
несоседние вершины.
D
С
E
В
Теорема: Сумма углов выпуклого
многоугольника (п – 2)·180°
F
А
K
Многоугольник называется выпуклым, если он лежит
по одну сторону от каждой прямой, проходящей через
две его соседние вершины.
Четырёхугольник – выпуклый многоугольник, у
3
которого 4 вершины и 4 стороны.

4.

Билет № 9.
1. Подобные треугольники. Определение. Коэффициент подобия. Отношение
периметров и площадей подобных треугольников.
2. Окружность с центром в точке O описана около равнобедренного
треугольника ABC, в котором AB = BC и угол ABC = 32°.
Найдите величину угла. BOC. Ответ дайте в градусах.
3. Найдите площадь прямоугольной трапеции АВСD, у которой
основания АВ и CD равны 12 и 20, а больший угол равен 135°.
3
4. В треугольнике АВС ∠С = 90°, cos В = 5, АВ = 45. Найдите АС.

5.

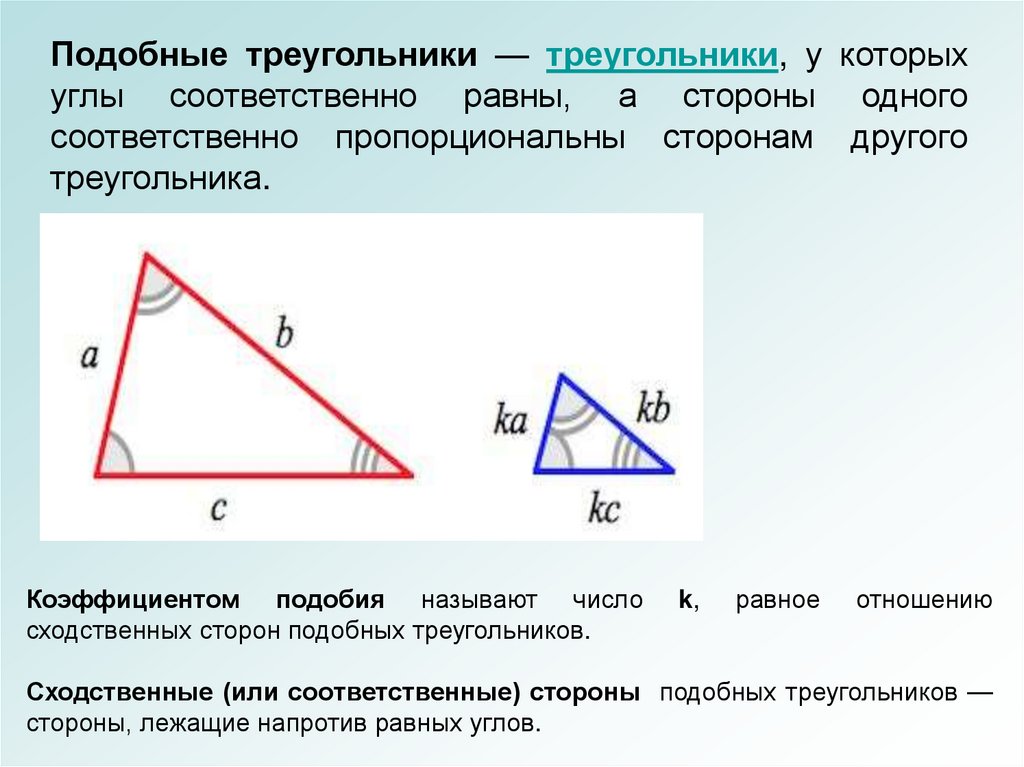
Подобные треугольники — треугольники, у которых
углы соответственно равны, а стороны одного
соответственно пропорциональны сторонам другого
треугольника.
Коэффициентом подобия называют число
сходственных сторон подобных треугольников.
k,
равное
отношению
Сходственные (или соответственные) стороны подобных треугольников —
стороны, лежащие напротив равных углов.

6.

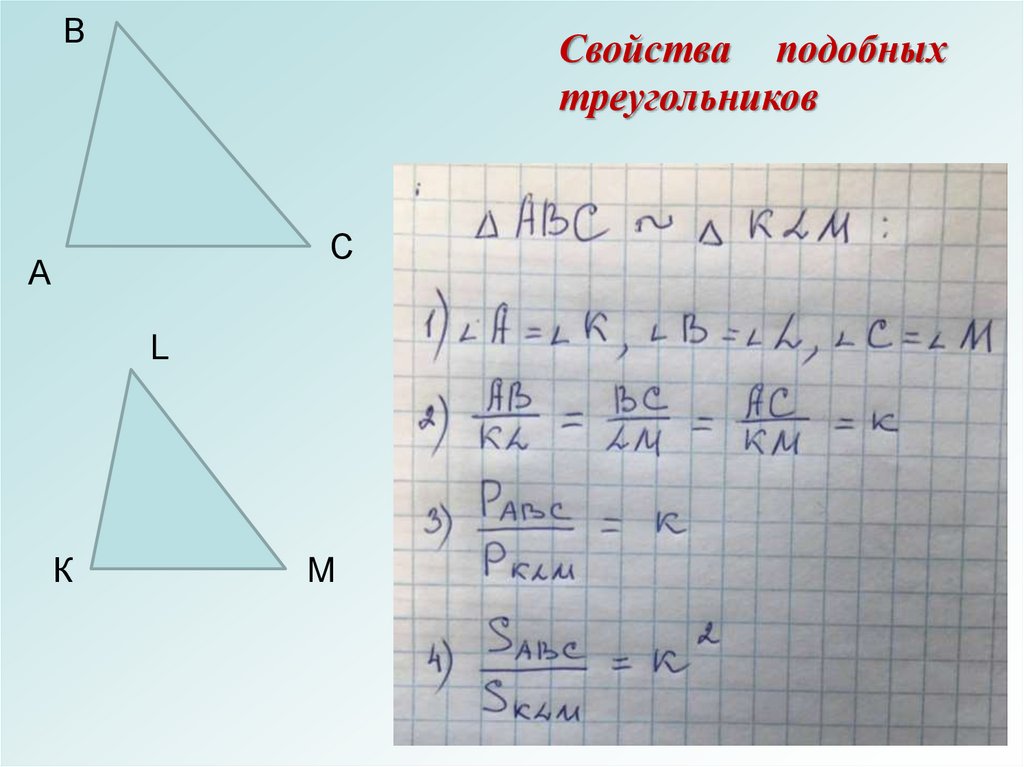
В
Свойства подобных
треугольников
С
А
L
К
M