Презентация_по_геометрии_для_10_класса_по_теме_Перпендикуляр_и_наклонная

1.

2. Урок №1

Расстояние от точки
до плоскости

3.

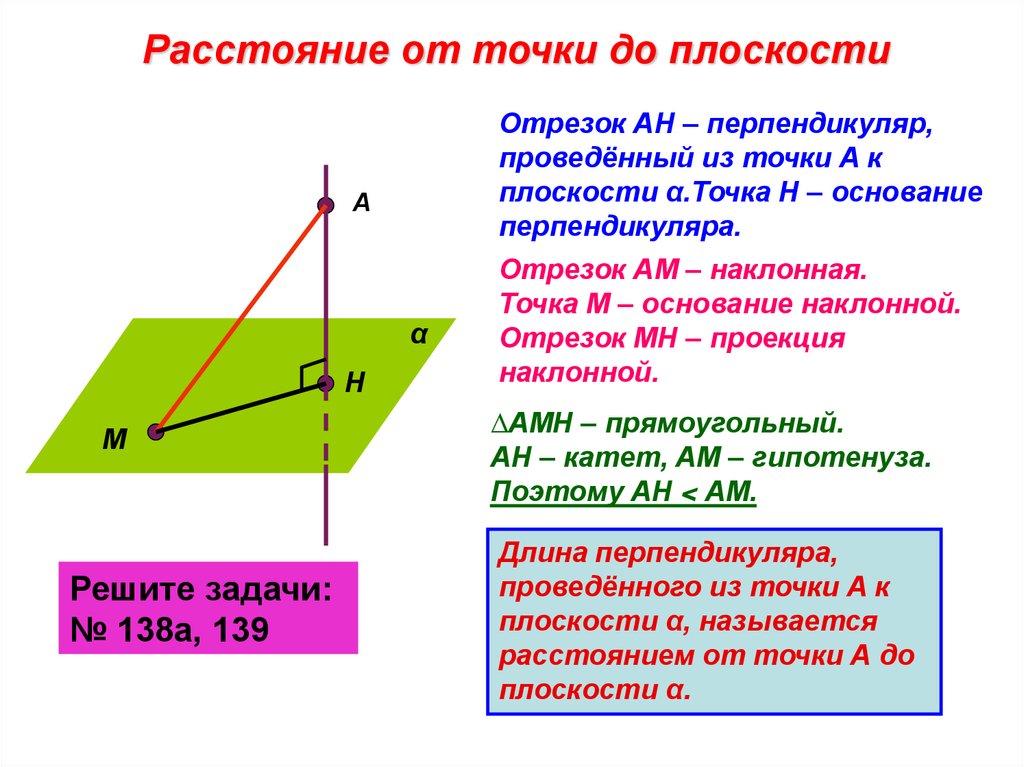
Расстояние от точки до плоскости
Отрезок АН – перпендикуляр,
проведённый из точки А к
плоскости α.Точка Н – основание
перпендикуляра.
А
α
Н
М
Решите задачи:
№ 138а, 139
Отрезок АМ – наклонная.
Точка М – основание наклонной.
Отрезок МН – проекция
наклонной.
∆АМН – прямоугольный.
АН – катет, АМ – гипотенуза.
Поэтому АН < АМ.
Длина перпендикуляра,
проведённого из точки А к
плоскости α, называется
расстоянием от точки А до
плоскости α.

4.

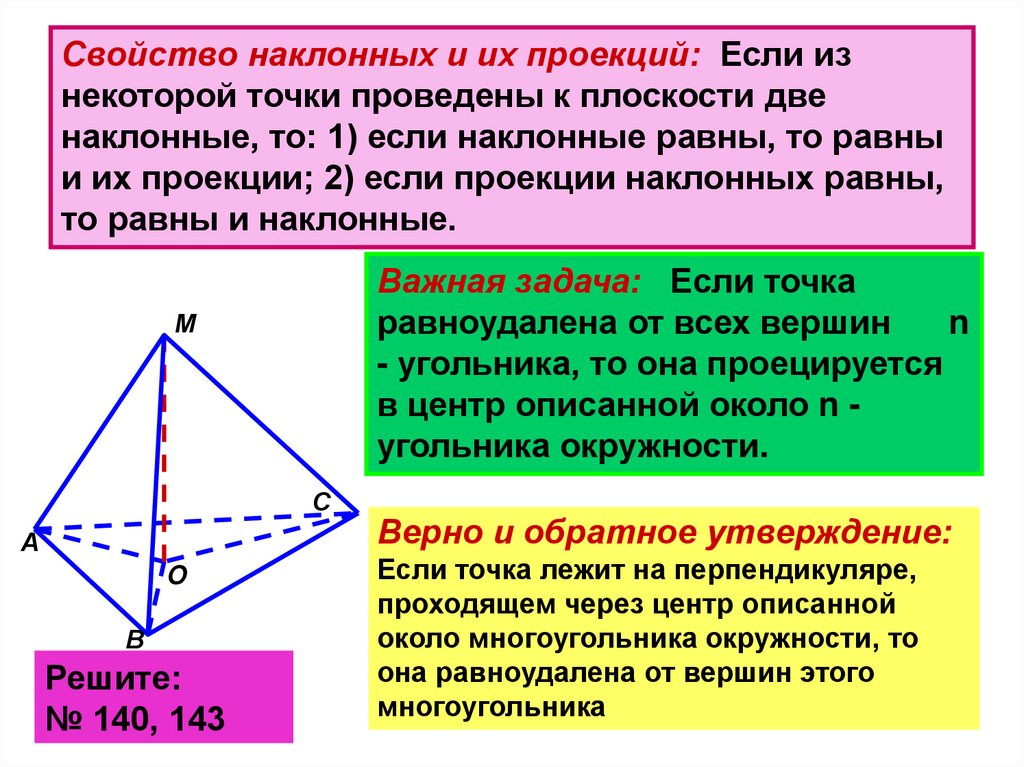
Свойство наклонных и их проекций: Если из
некоторой точки проведены к плоскости две
наклонные, то: 1) если наклонные равны, то равны
и их проекции; 2) если проекции наклонных равны,
то равны и наклонные.
Важная задача: Если точка
равноудалена от всех вершин
n
- угольника, то она проецируется
в центр описанной около n угольника окружности.
М
С
А
O
В
Решите:
№ 140, 143
Верно и обратное утверждение:
Если точка лежит на перпендикуляре,
проходящем через центр описанной
около многоугольника окружности, то
она равноудалена от вершин этого
многоугольника

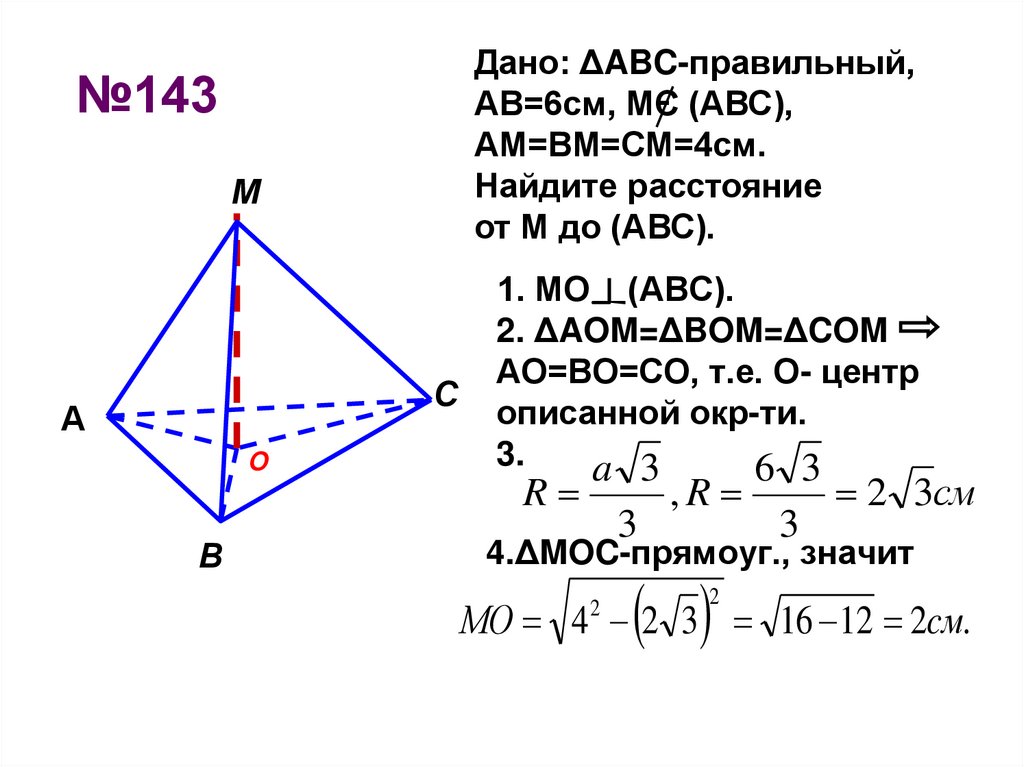
5. №143

Дано: ΔABC-правильный,
АВ=6см, МЄ (АВС),
АМ=ВМ=СМ=4см.
Найдите расстояние
от М до (АВС).
№143
М
С
А
O
В
1. МО (АВС).
2. ΔAOM=ΔBOM=ΔCOM
АО=ВО=СО, т.е. О- центр
описанной окр-ти.
3.
a 3
6 3
R
3
,R
3
2 3см
4.ΔMOC-прямоуг., значит
2
МО 4 2 3 16 12 2cм.
2

6.

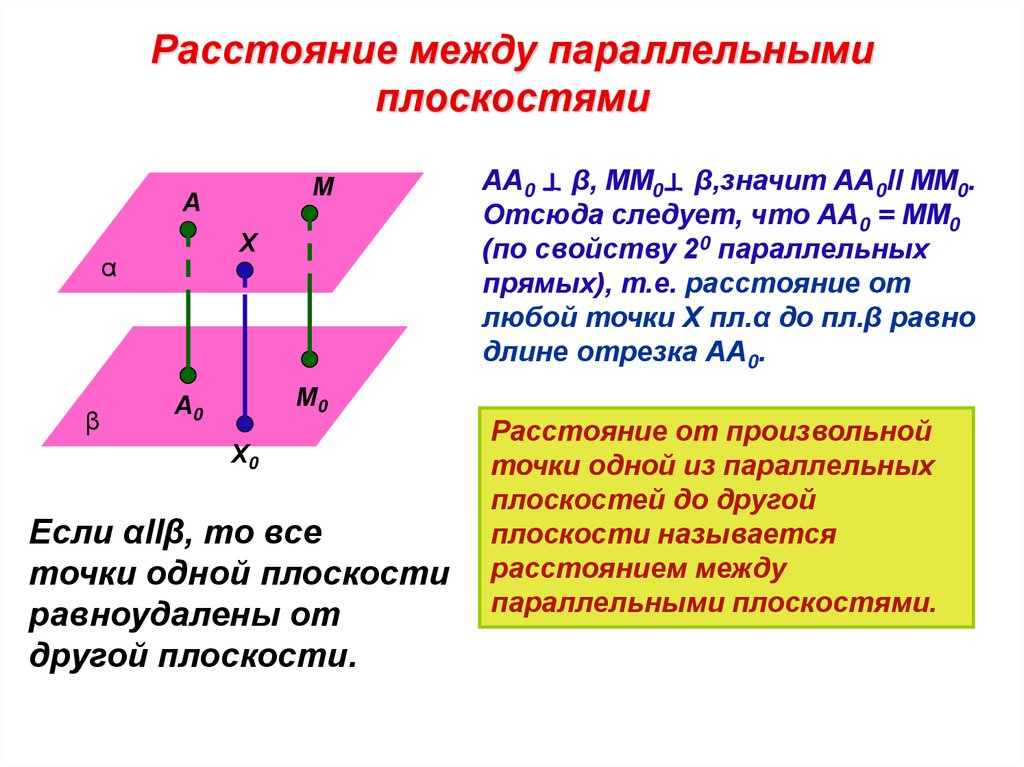
Расстояние между параллельными
плоскостями
М
А
Х
α
β
М0
А0
Х0
Если αllβ, то все
точки одной плоскости
равноудалены от
другой плоскости.
АА0 β, ММ0 β,значит АА0ll ММ0.
Отсюда следует, что АА0 = ММ0
(по свойству 20 параллельных
прямых), т.е. расстояние от
любой точки Х пл.α до пл.β равно
длине отрезка АА0.
Расстояние от произвольной
точки одной из параллельных
плоскостей до другой
плоскости называется
расстоянием между
параллельными плоскостями.

7.

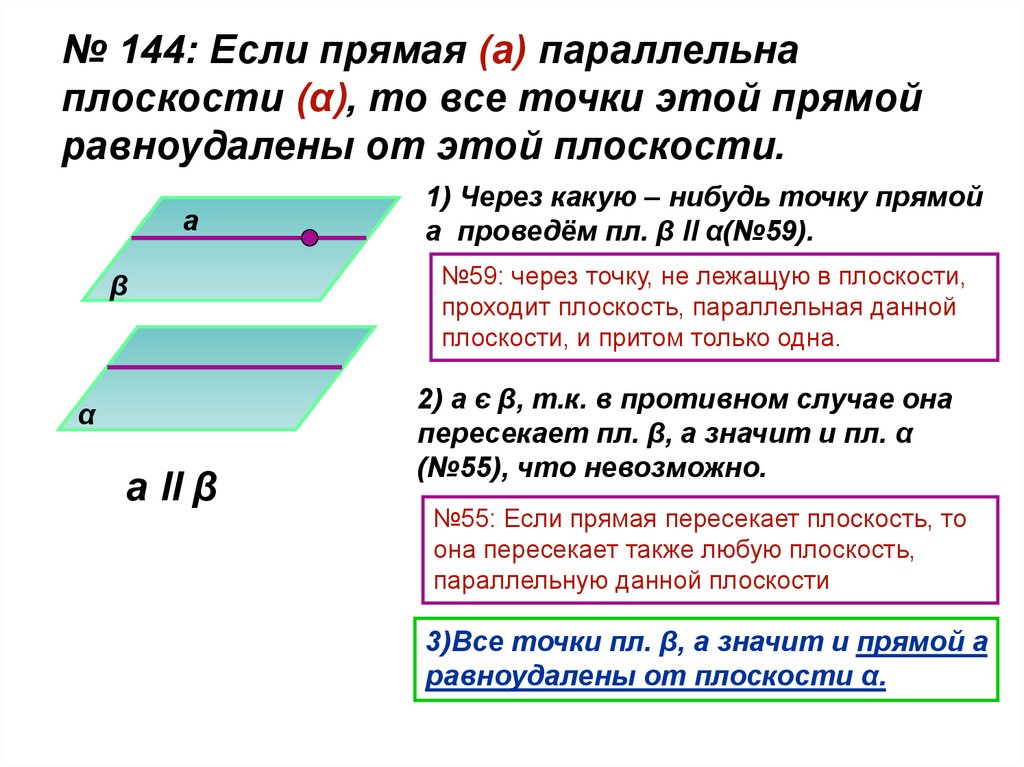
№ 144: Если прямая (а) параллельна
плоскости (α), то все точки этой прямой
равноудалены от этой плоскости.
а
β
α
а ll β
1) Через какую – нибудь точку прямой
а проведём пл. β ll α(№59).
№59: через точку, не лежащую в плоскости,
проходит плоскость, параллельная данной
плоскости, и притом только одна.
2) а є β, т.к. в противном случае она
пересекает пл. β, а значит и пл. α
(№55), что невозможно.
№55: Если прямая пересекает плоскость, то
она пересекает также любую плоскость,
параллельную данной плоскости
3)Все точки пл. β, а значит и прямой а
равноудалены от плоскости α.

8.

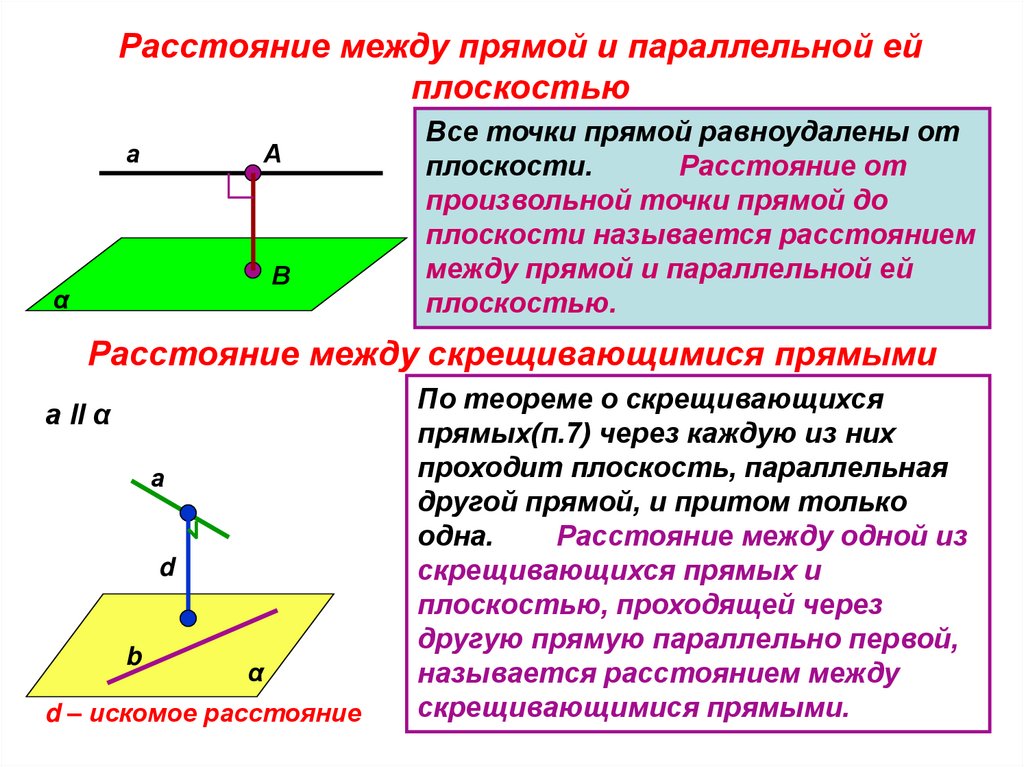
Расстояние между прямой и параллельной ей
плоскостью
а
А
В
α
Все точки прямой равноудалены от
плоскости.
Расстояние от
произвольной точки прямой до
плоскости называется расстоянием
между прямой и параллельной ей
плоскостью.
Расстояние между скрещивающимися прямыми
а ll α
а
d
b
α
d – искомое расстояние
По теореме о скрещивающихся
прямых(п.7) через каждую из них
проходит плоскость, параллельная
другой прямой, и притом только
одна.
Расстояние между одной из
скрещивающихся прямых и
плоскостью, проходящей через
другую прямую параллельно первой,
называется расстоянием между
скрещивающимися прямыми.

9. Решение задач: №138а,139,140,143

Домашнее задание:
п.19, № 138б, 141, 142.
Законспектировать пункт 19
из замечания: расстояния
от точки до …, между…

10. Урок 2

Теорема
о трёх перпендикулярах

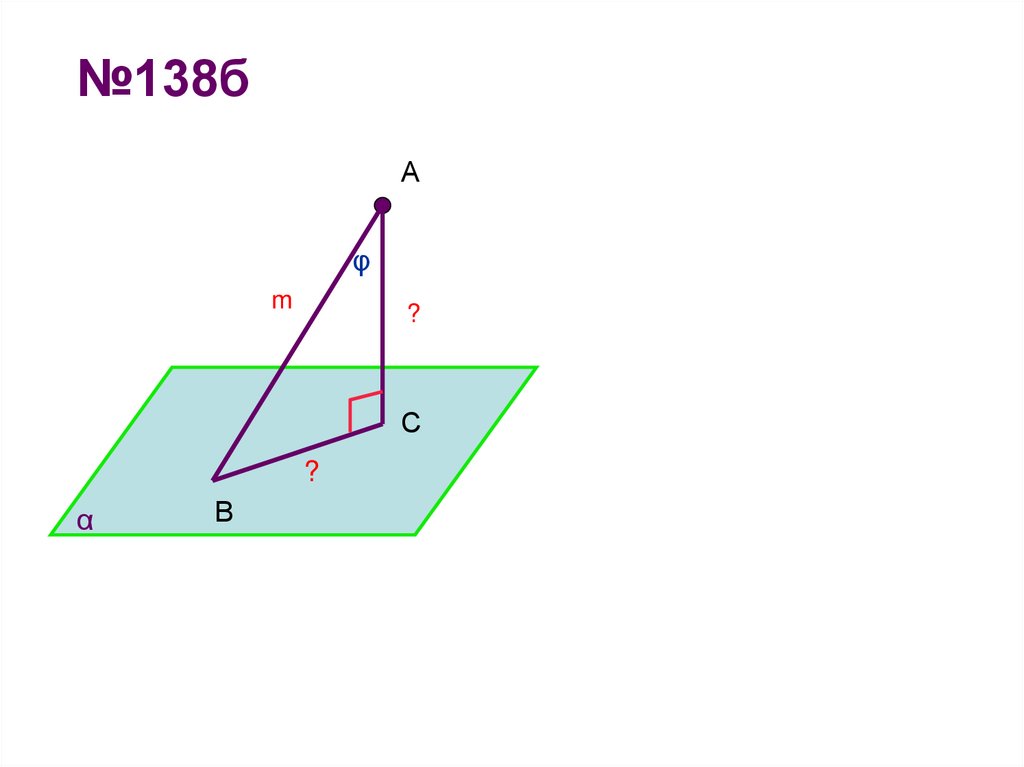
11. №138б

А
φ
m
?
С
?
α
В

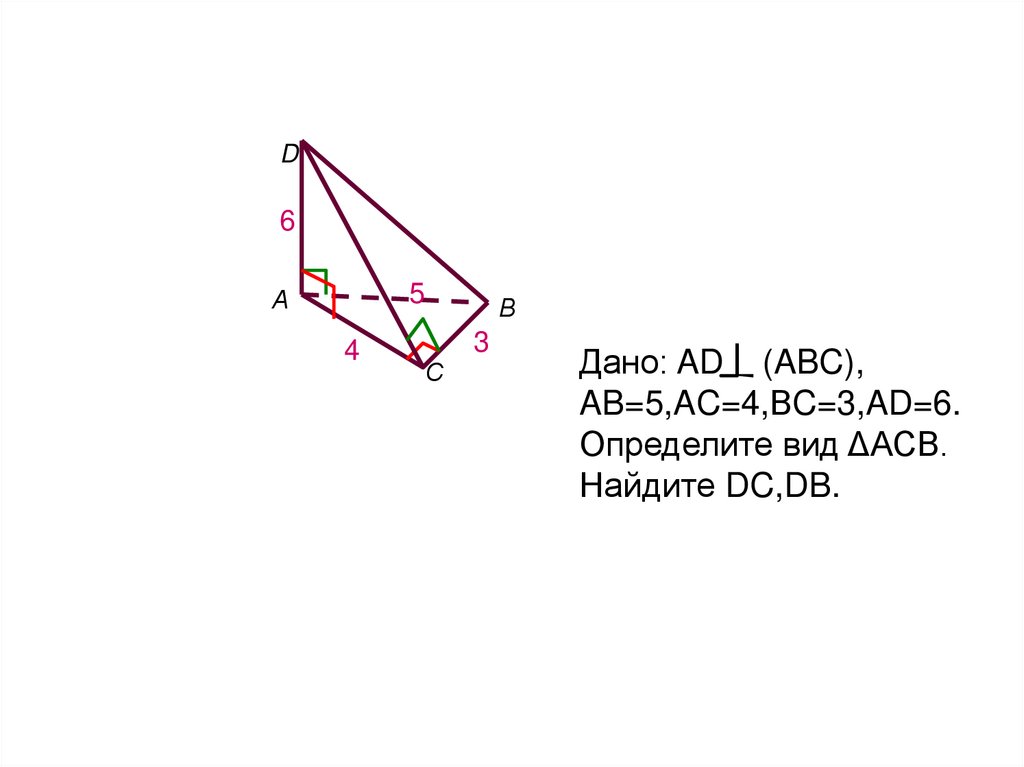
12.

D
6
5
А
4
В
3
С
Дано: AD (ABC),
AB=5,AC=4,ВC=3,AD=6.
Определите вид ΔАСВ.
Найдите DC,DB.

13.

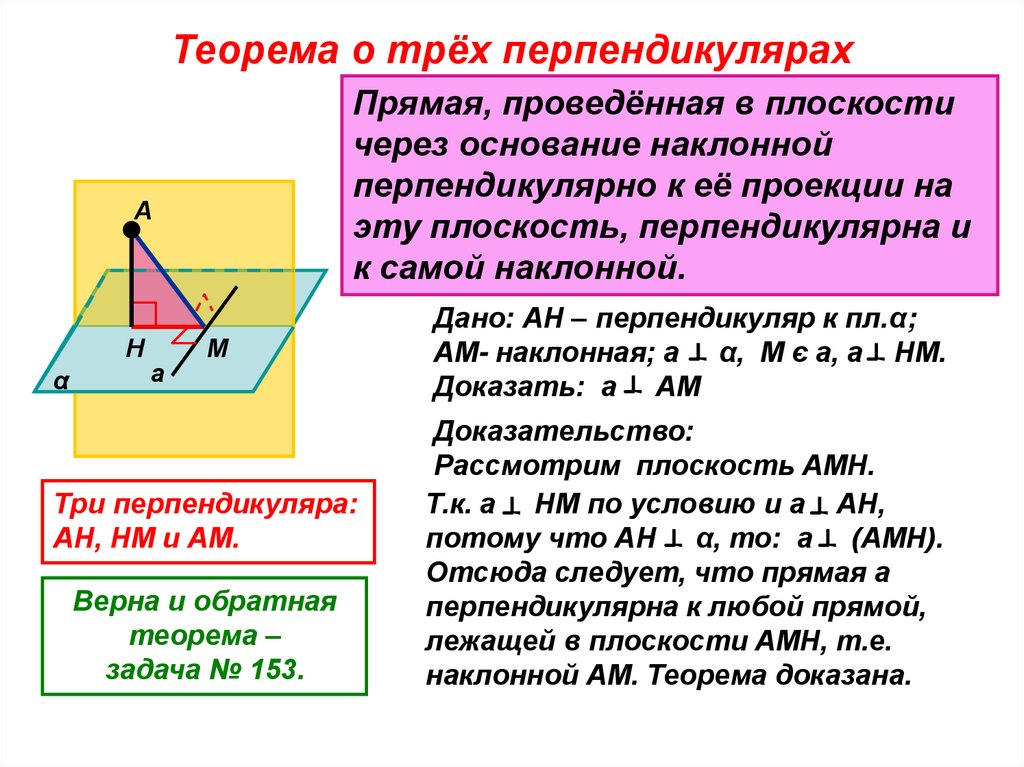
Теорема о трёх перпендикулярах
Прямая, проведённая в плоскости
через основание наклонной
перпендикулярно к её проекции на
эту плоскость, перпендикулярна и
к самой наклонной.
А
Н
α
а
М
Три перпендикуляра:
АН, НМ и АМ.
Верна и обратная
теорема –
задача № 153.
Дано: АН – перпендикуляр к пл.α;
АМ- наклонная; а α, М є а, а НМ.
Доказать: а АМ
Доказательство:
Рассмотрим плоскость АМН.
Т.к. а НМ по условию и а АН,
потому что АН α, то: а (АМН).
Отсюда следует, что прямая а
перпендикулярна к любой прямой,
лежащей в плоскости АМН, т.е.
наклонной АМ. Теорема доказана.

14.

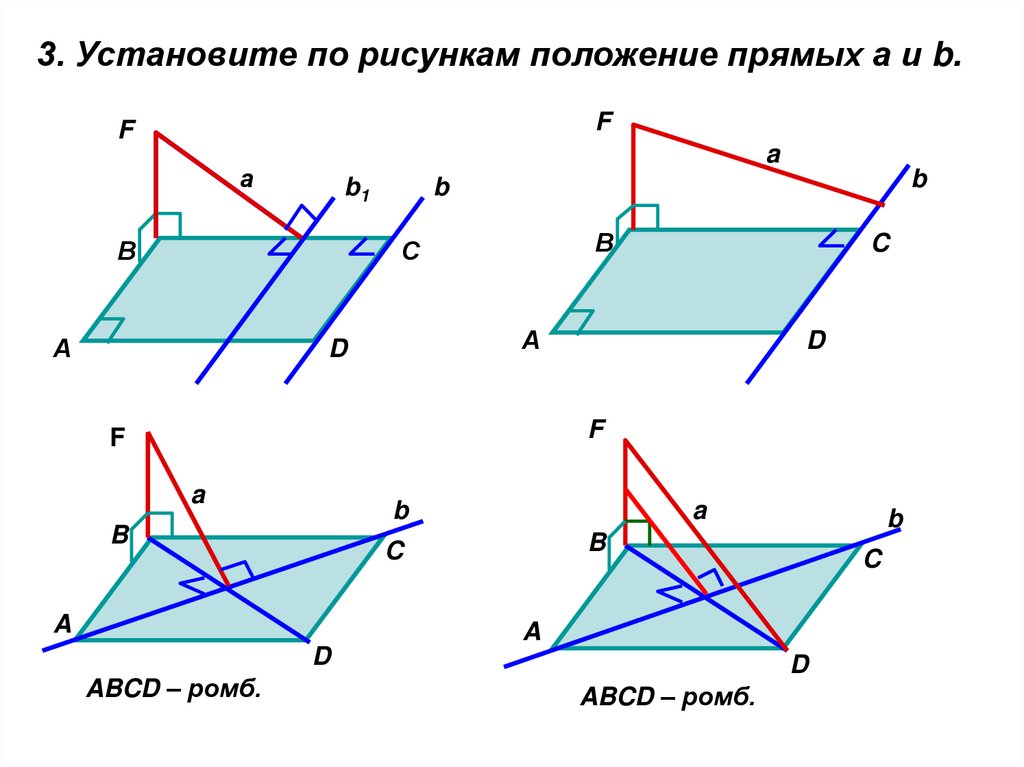
3. Установите по рисункам положение прямых а и b.
F
F
a
а
b1
В
b
b
В
С
А
C
А
D
D
F
F
a
b
B
a
B
C
A
b
C
A
D
ABCD – ромб.
D
ABCD – ромб.

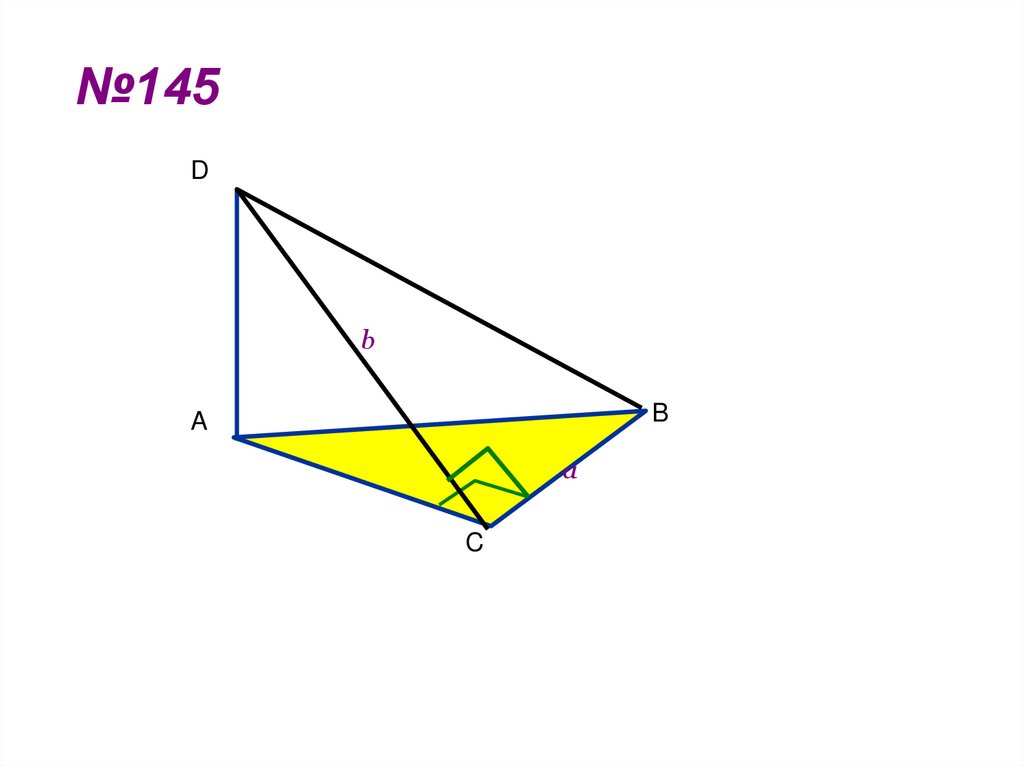
15. №145

D
b
B
A
a
C

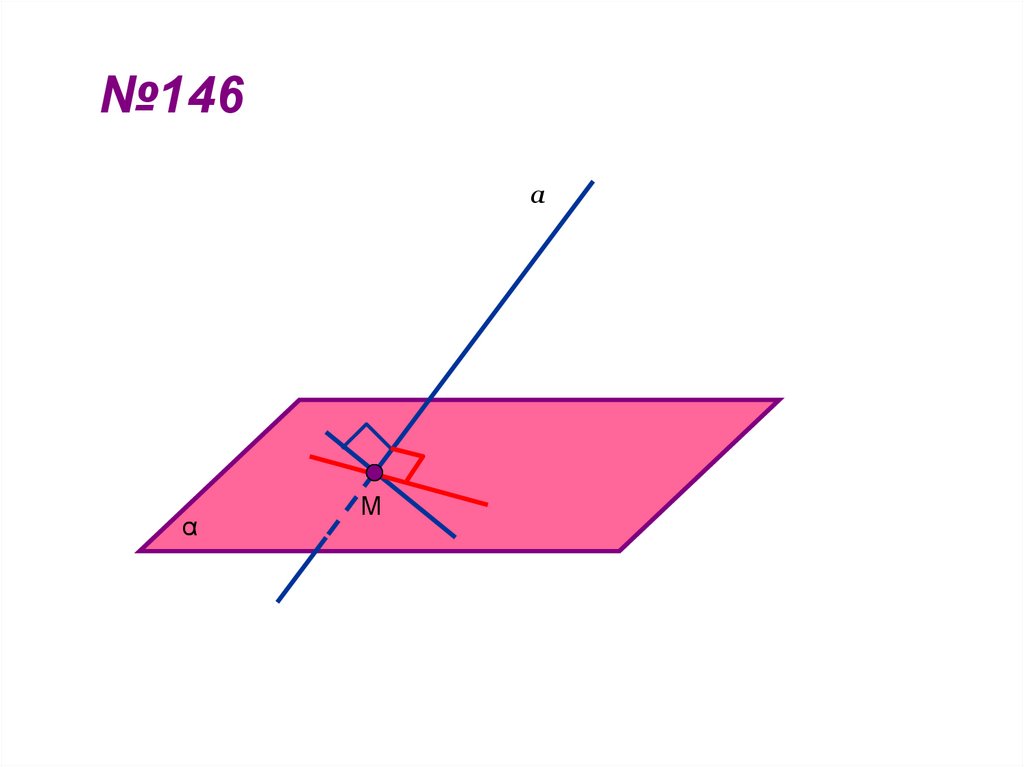
16. №146

а
α
М

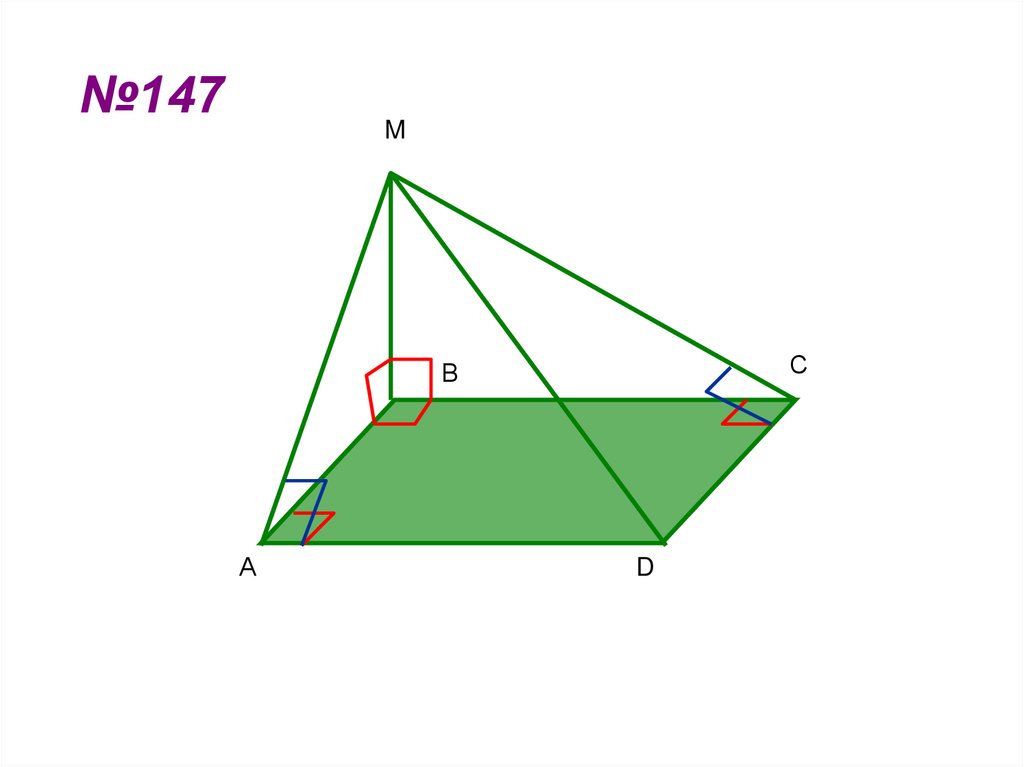
17. №147

M
С
В
А
D

18. Домашнее задание: № 148,149,150

19.

Урок 3
Решение задач по теме
«Теорема о трёх перпендикулярах»

20.

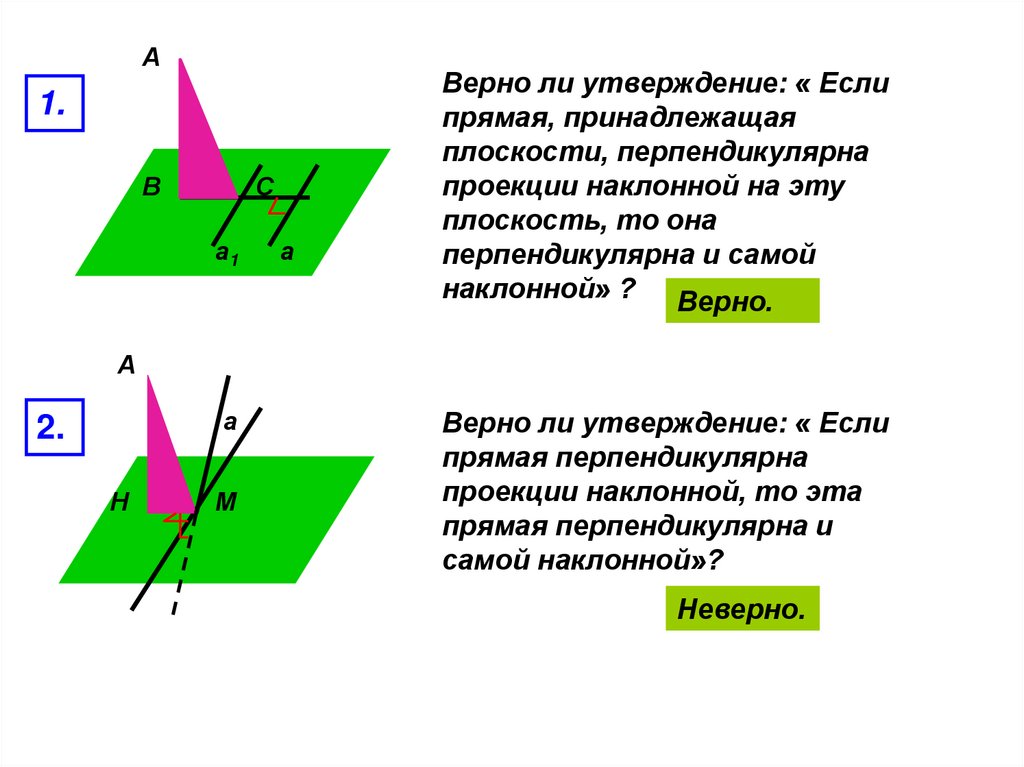
А
1.
В
С
а1
а
Верно ли утверждение: « Если
прямая, принадлежащая
плоскости, перпендикулярна
проекции наклонной на эту
плоскость, то она
перпендикулярна и самой
наклонной» ? Верно.
А
а
2.
Н
М
Верно ли утверждение: « Если
прямая перпендикулярна
проекции наклонной, то эта
прямая перпендикулярна и
самой наклонной»?
Неверно.

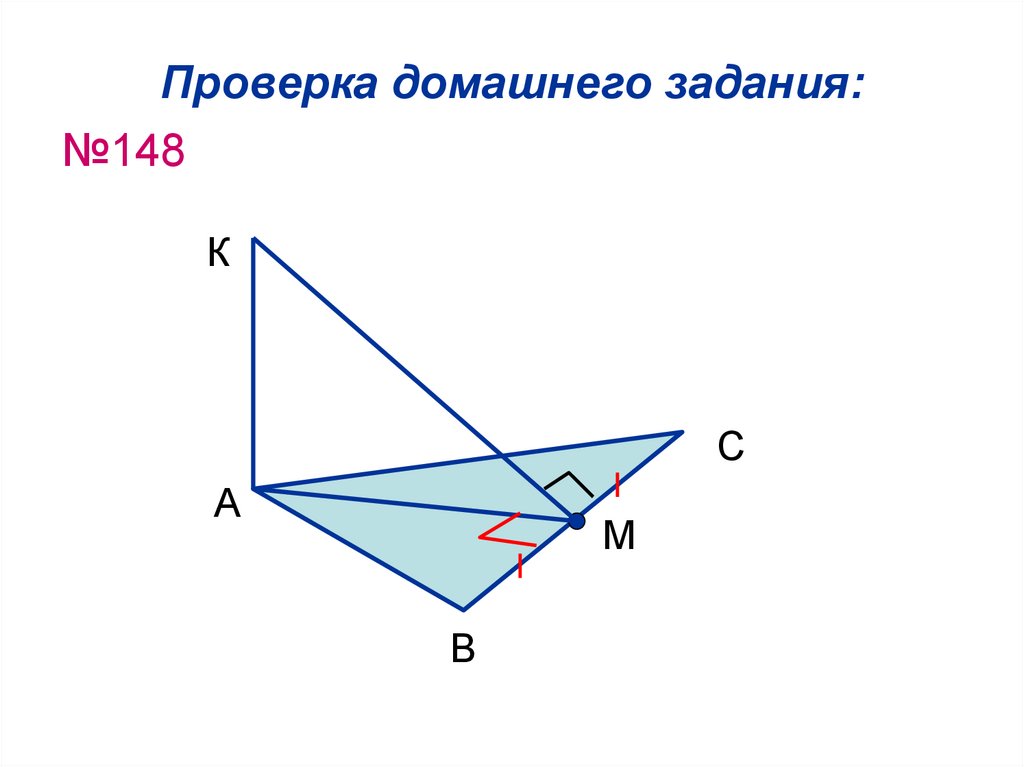
21. Проверка домашнего задания:

№148
К
С
А
М
В

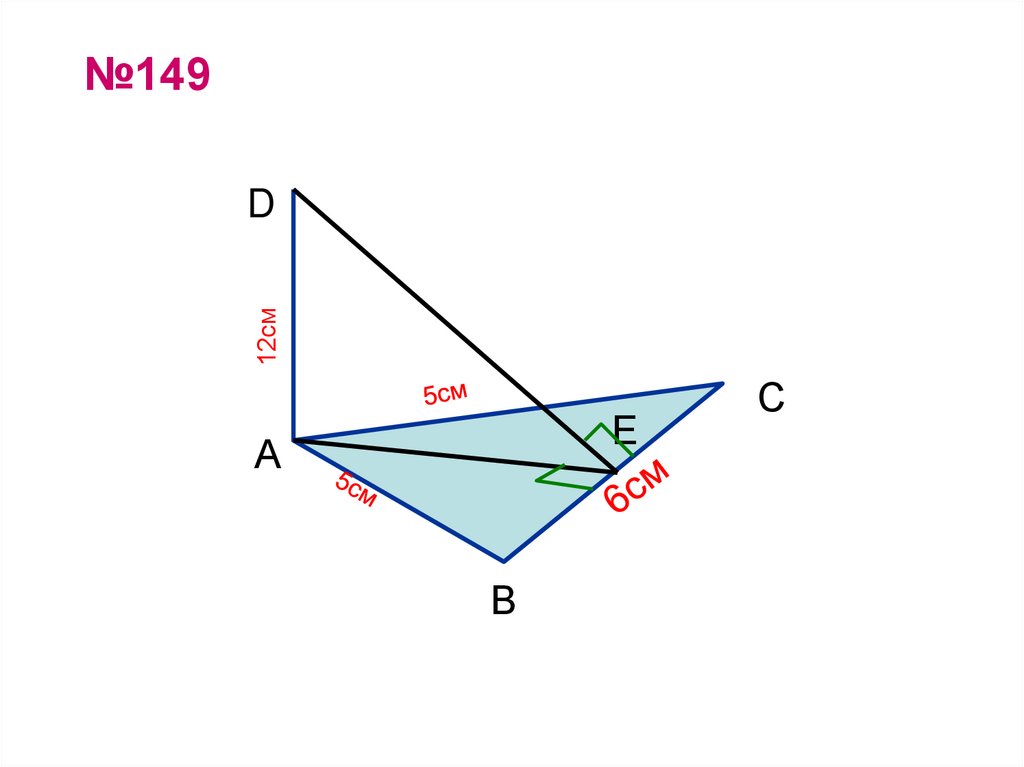
22. №149

12см
D
Е
А
В
С

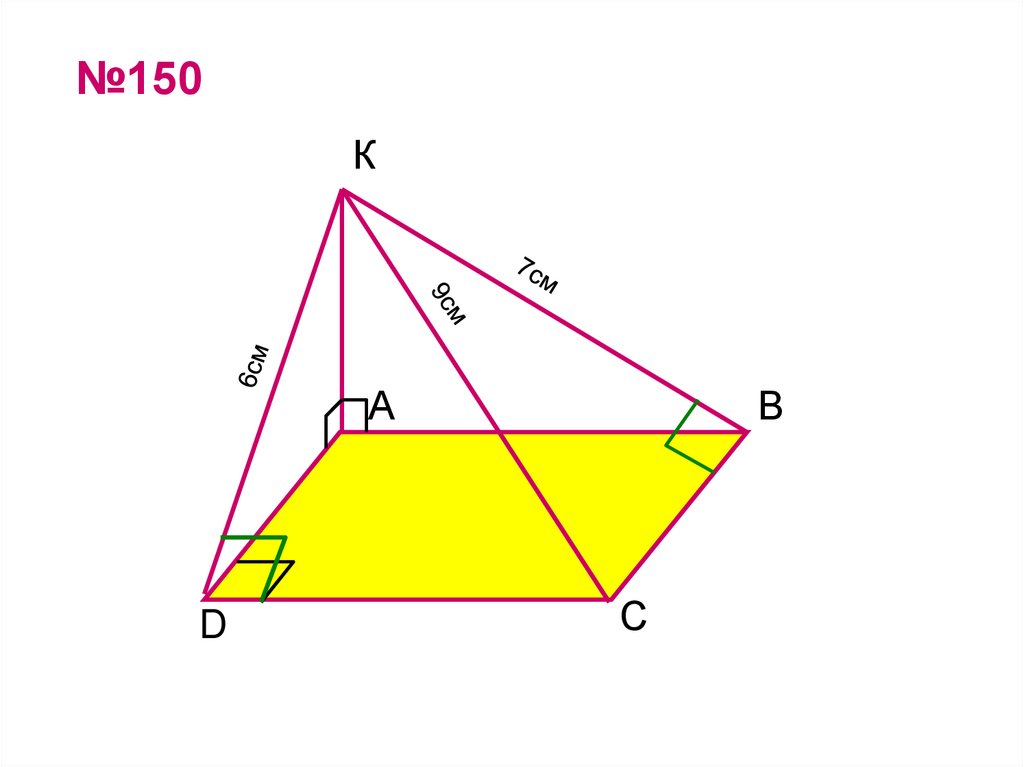
23. №150

К
2см
А
В
4 2см
D
45см
С

24.

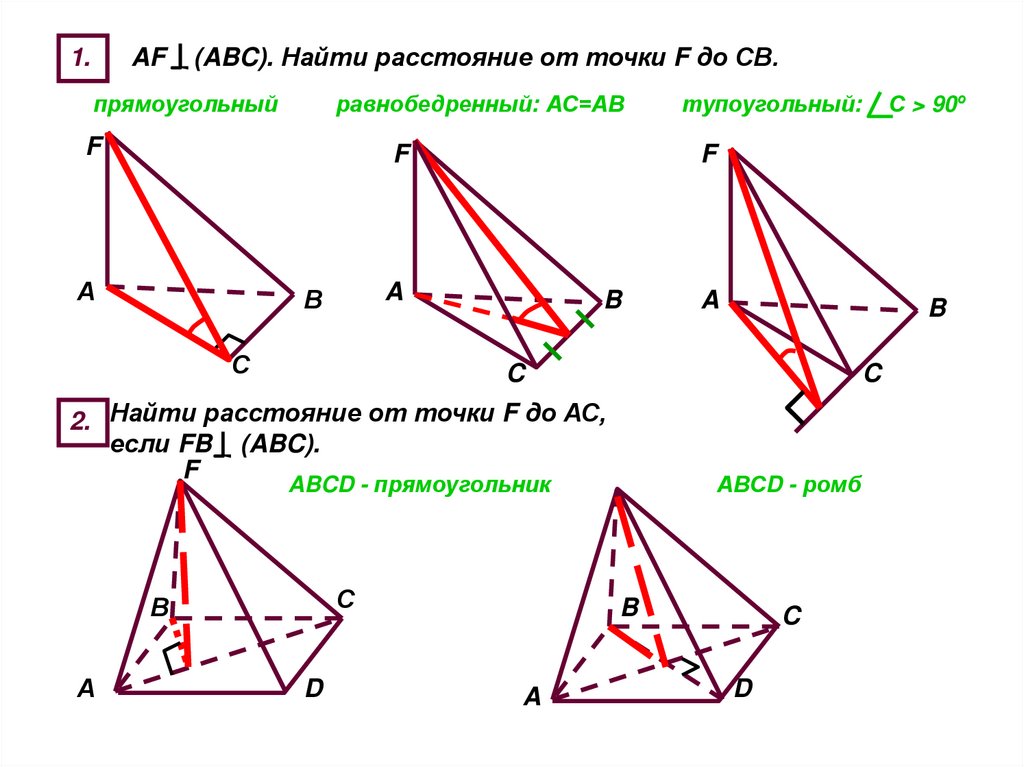
1.
AF
(ABC). Найти расстояние от точки F до СВ.
прямоугольный
равнобедренный: АС=АВ
F
F
А
С
B
B
C
2. Найти расстояние от точки F до АС,
если FB (ABC).
F
ABCD - прямоугольник
А
A
C
С
В
D
С > 90º
F
A
В
тупоугольный:
АВСD - ромб
B
A
C
D

25.

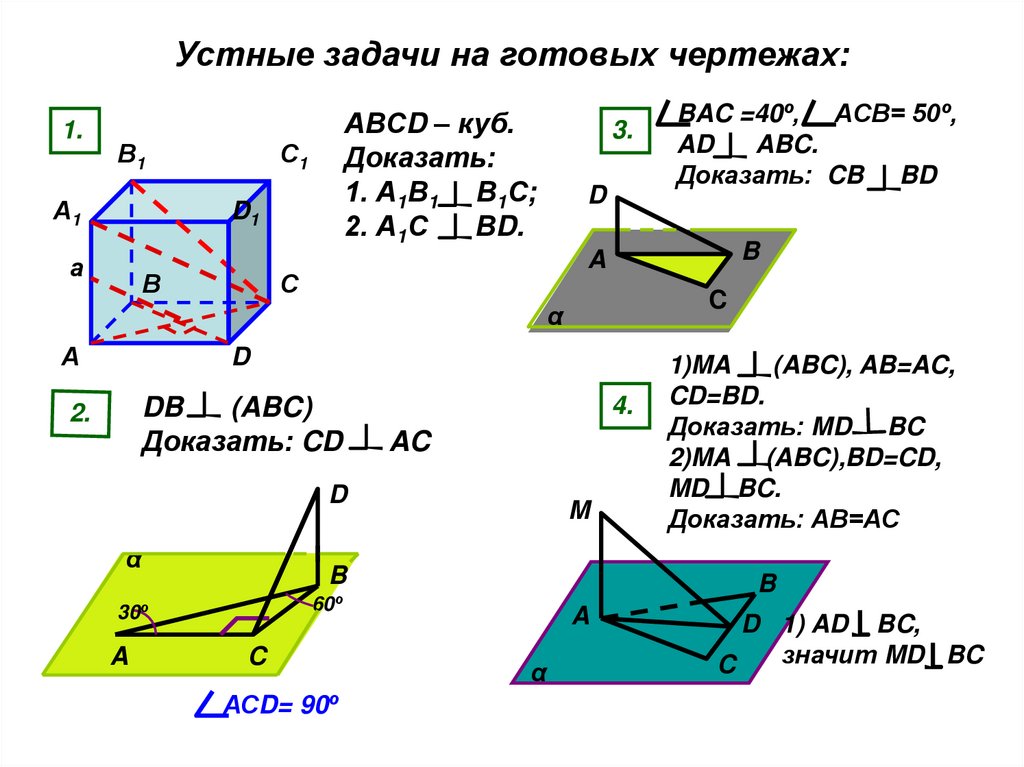
Устные задачи на готовых чертежах:
1.
В1
А1
АВСD – куб.
Доказать:
1. А1В1 В1С;
2. А1С
ВD.
С1
D1
а
В
3.
D
B
A
С
C
α
А
D
2.
DB
(ABC)
Доказать: CD
4.
AC
D
α
A
M
B
C
АСD= 90º
1)MA
(ABC), AB=AC,
CD=BD.
Доказать: MD BC
2)MA (ABC),BD=CD,
MD BC.
Доказать: АВ=АС
B
60º
30º
BAC =40º, ACB= 50º,
AD
ABC.
Доказать: CB BD
A
α
D 1) AD BC,
значит MD BC
C

26.

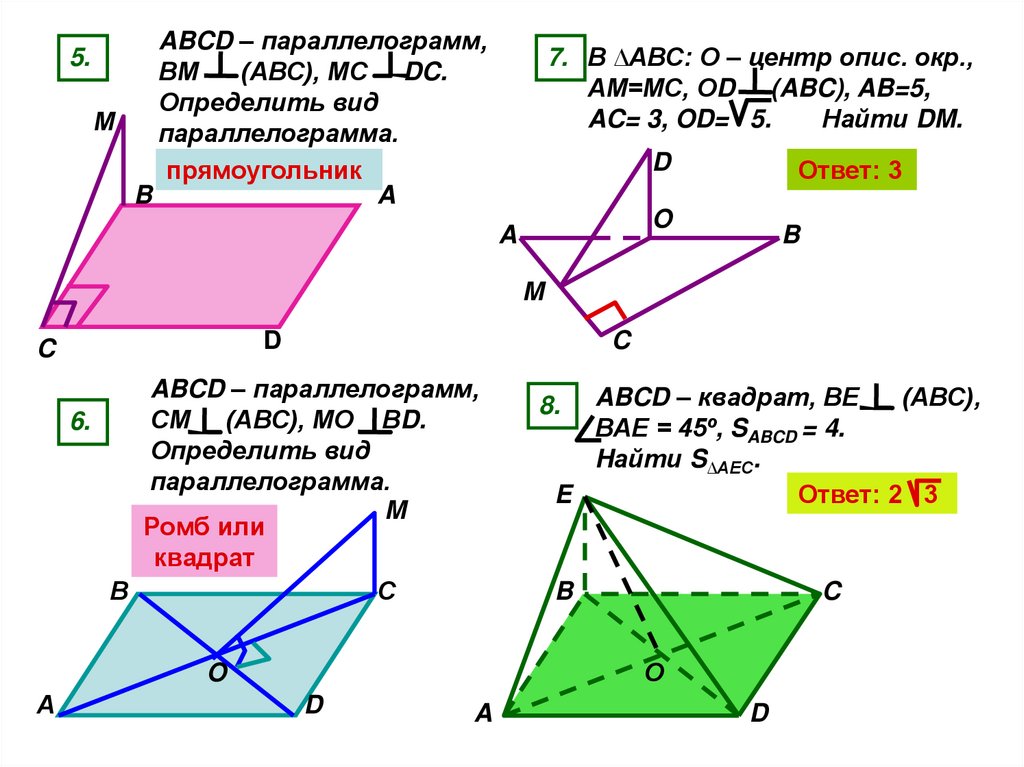
5.
ABCD – параллелограмм,
ВМ
(АВС), МС DC.
Определить вид
М
параллелограмма.
прямоугольник
B
A
7. В ∆АВС: О – центр опис. окр.,
АМ=МС, ОD (ABC), AB=5,
AC= 3, OD= 5.
Найти DM.
D
Ответ: 3
O
A
B
M
D
C
C
ABCD – параллелограмм,
СМ (АВС), МО ВD.
6.
Определить вид
параллелограмма.
M
Ромб или
квадрат
В
С
B
C
О
O
А
ABCD – квадрат, ВЕ
(АВС),
ВАЕ = 45º, SABCD = 4.
Hайти S∆AEC.
E
Ответ: 2 3
8.
D
A
D

27. Решение задач: №154,156. Домашнее задание: №155, 159.

28.

Урок 4
Решение задач по теме
«Теорема о трёх перпендикулярах»

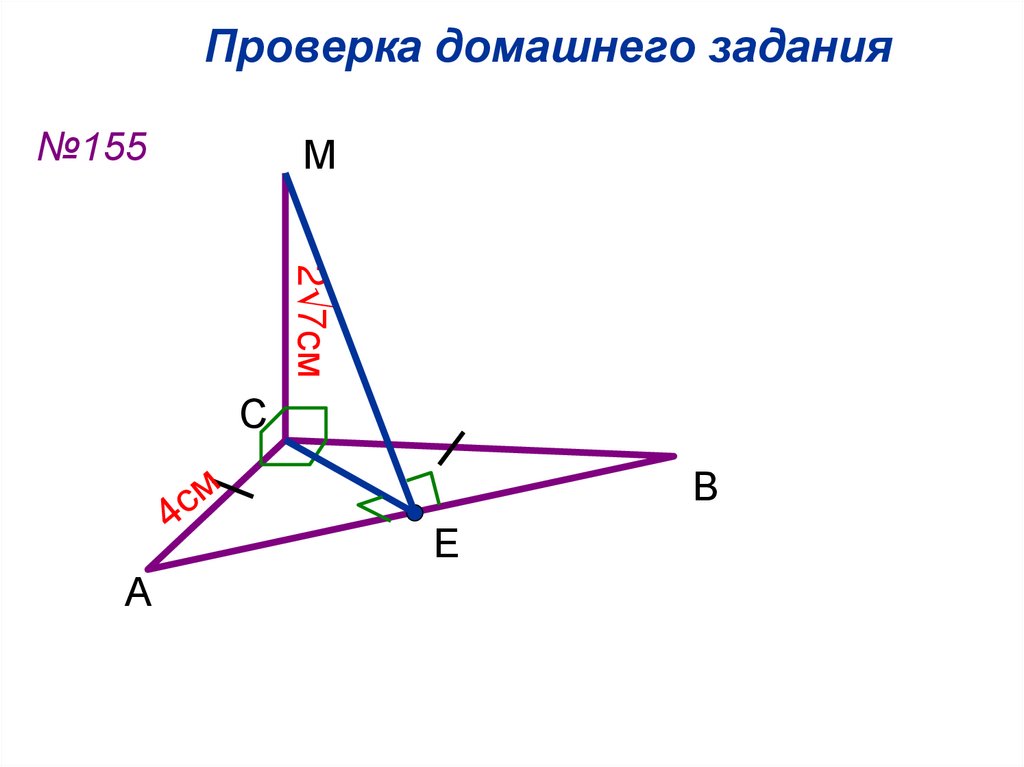
29. Проверка домашнего задания

№155
М
2√7см
АЕ=ВЕ=СЕ=2√2см,
МЕ2=(2√7)2+(2√2)2=
=28+8=36,
МЕ = 6(см)
С
В
Е
А

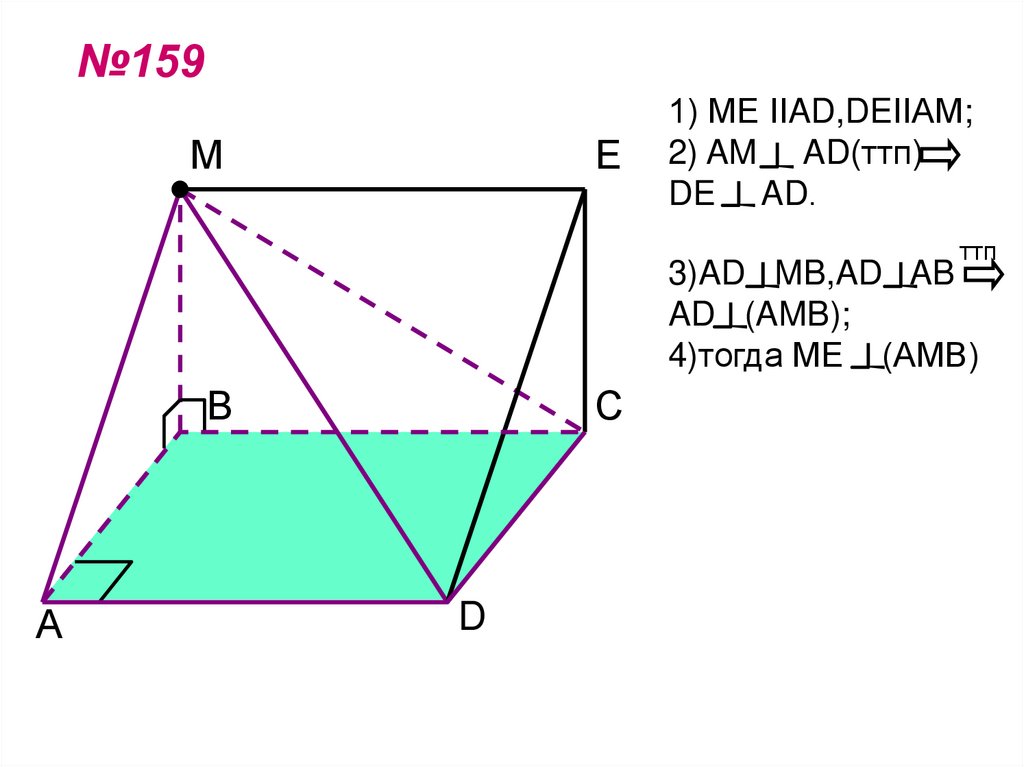
30. №159

М
Е
1) МЕ ІІAD,DEІІΑМ;
2) AM AD(ттп)
DE AD.
ттп
3)AD MB,AD AB
AD (AMB);
4)тогда МЕ (АМВ)
В
А
С
D

31.

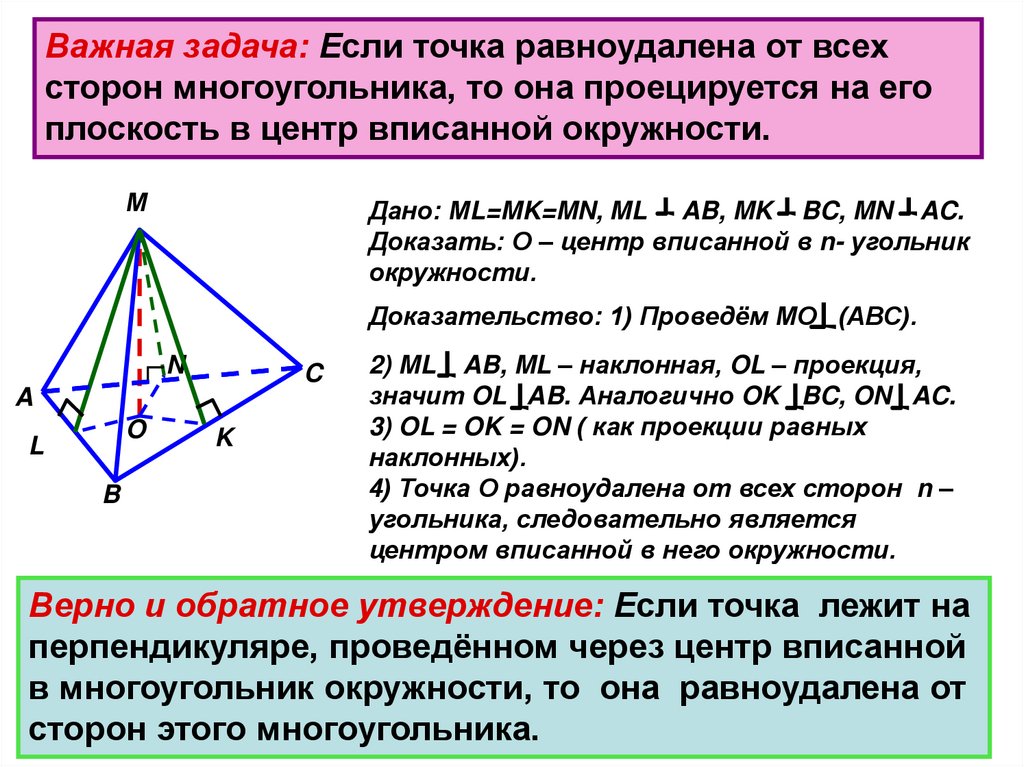
Важная задача: Если точка равноудалена от всех
сторон многоугольника, то она проецируется на его
плоскость в центр вписанной окружности.
М
Дано: МL=MK=MN, ML AB, MK BC, MN AC.
Доказать: О – центр вписанной в n- угольник
окружности.
Доказательство: 1) Проведём МО (АВС).
N
C
A
O
L
B
K
2) ML AB, ML – наклонная, OL – проекция,
значит OL AB. Аналогично OK BC, ON AC.
3) OL = OK = ON ( как проекции равных
наклонных).
4) Точка О равноудалена от всех сторон n –
угольника, следовательно является
центром вписанной в него окружности.
Верно и обратное утверждение: Если точка лежит на
перпендикуляре, проведённом через центр вписанной
в многоугольник окружности, то она равноудалена от
сторон этого многоугольника.

32. Решение задач по готовым рисункам из урока 10

Домашнее задание:
№ 160, 205

33.

Урок 5
Угол между прямой и плоскостью

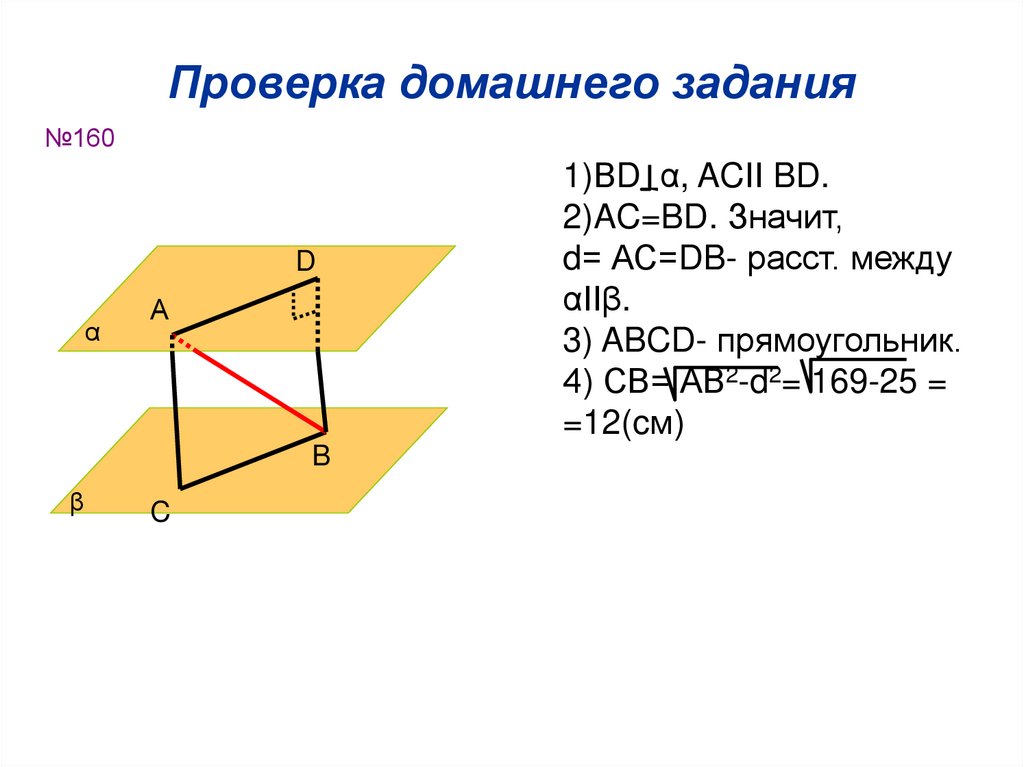
34. Проверка домашнего задания

№160
D
α
А
B
β
C
1)ВD α, ACІІ BD.
2)AC=BD. Значит,
d= АС=DB- расст. между
αІІβ.
3) ABCD- прямоугольник.
4) СВ= АВ2-d2= 169-25 =
=12(cм)

35.

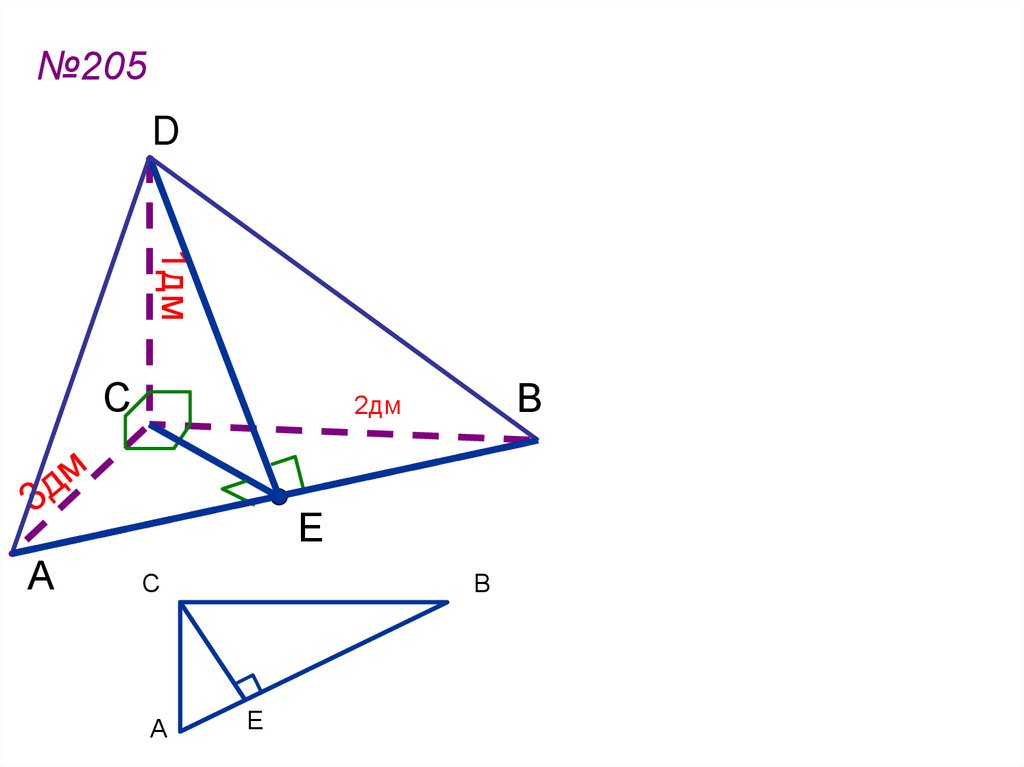
АВ АС 2 ВС 2
№205
9 4 13 дм ,
CA
3
АЕ=ВЕ=СЕ=2√2см,
cos A
cos BCE ,
2=
AB 2+(2√2)
13
МЕ2=(2√7)
=28+8=36, CE CE
cos BCE
,
МЕ = 6(см)BC 2
3
CE
6
дм ,
, CE
В
13 2
13
D
1дм
С
2дм
Е
А
С
А
В
Е
36
7
DE 1
,
13
13
1
1
7
S AB DE 13
3,5.
2
2
13

36.

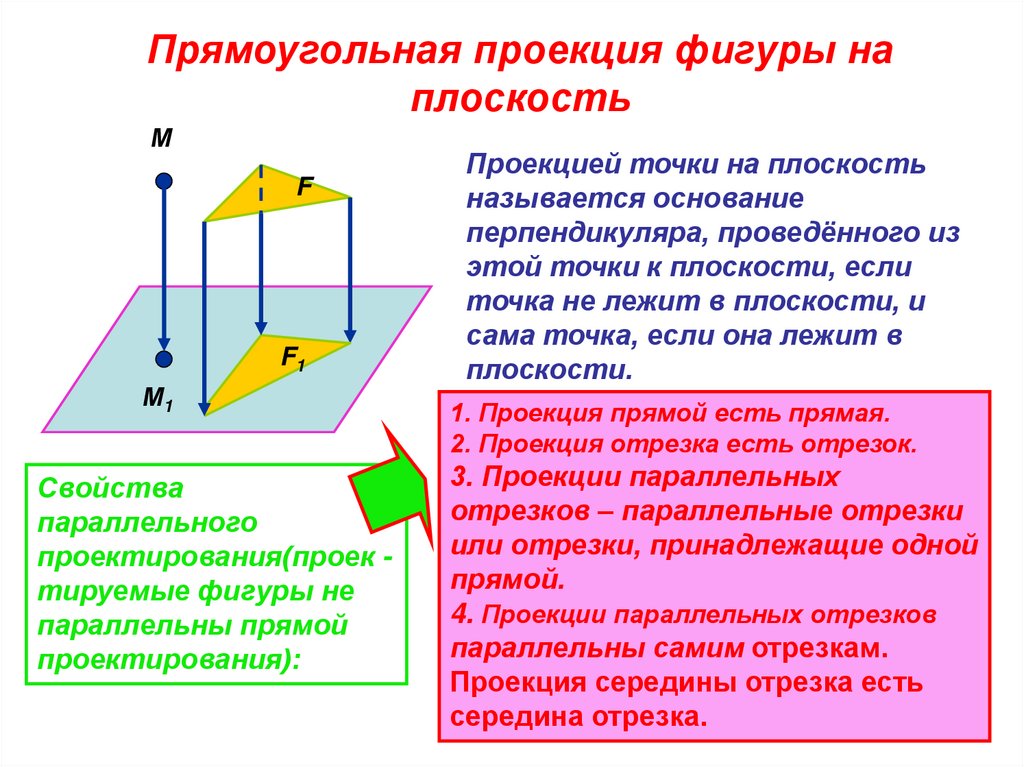
Прямоугольная проекция фигуры на
плоскость
М
F
F1
М1
Свойства
параллельного
проектирования(проек тируемые фигуры не
параллельны прямой
проектирования):
Проекцией точки на плоскость
называется основание
перпендикуляра, проведённого из
этой точки к плоскости, если
точка не лежит в плоскости, и
сама точка, если она лежит в
плоскости.
1. Проекция прямой есть прямая.
2. Проекция отрезка есть отрезок.
3. Проекции параллельных
отрезков – параллельные отрезки
или отрезки, принадлежащие одной
прямой.
4. Проекции параллельных отрезков
параллельны самим отрезкам.
Проекция середины отрезка есть
середина отрезка.

37.

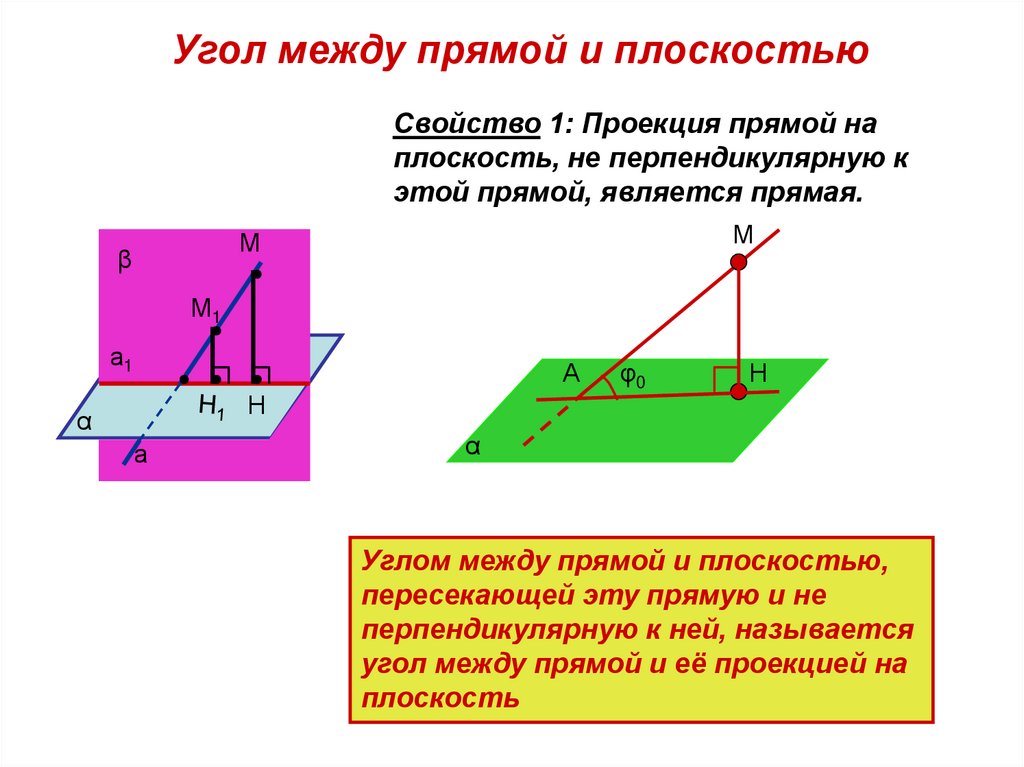
Угол между прямой и плоскостью
Свойство 1: Проекция прямой на
плоскость, не перпендикулярную к
этой прямой, является прямая.
М
М
β
М1
а1
А
Н
α
а
φ0
Н
α
Углом между прямой и плоскостью,
пересекающей эту прямую и не
перпендикулярную к ней, называется
угол между прямой и её проекцией на
плоскость

38.

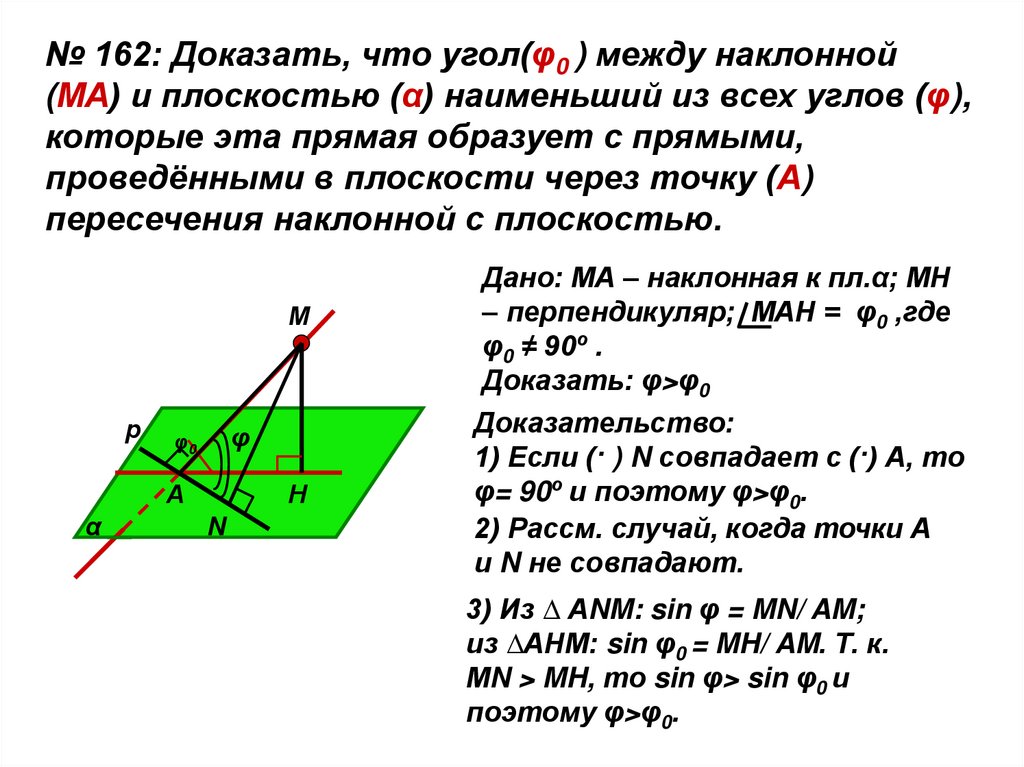
№ 162: Доказать, что угол(φ0 ) между наклонной
(МА) и плоскостью (α) наименьший из всех углов (φ),
которые эта прямая образует с прямыми,
проведёнными в плоскости через точку (А)
пересечения наклонной с плоскостью.
М
р
φ
φ0
А
α
Н
N
Дано: МА – наклонная к пл.α; МН
– перпендикуляр; МАН = φ0 ,где
φ0 ≠ 90º .
Доказать: φ>φ0
Доказательство:
1) Если (· ) N совпадает с (·) А, то
φ= 90º и поэтому φ>φ0.
2) Рассм. случай, когда точки А
и N не совпадают.
3) Из ∆ АNM: sin φ = MN/ AM;
из ∆АНМ: sin φ0 = MH/ AM. Т. к.
МN > MH, то sin φ> sin φ0 и
поэтому φ>φ0.

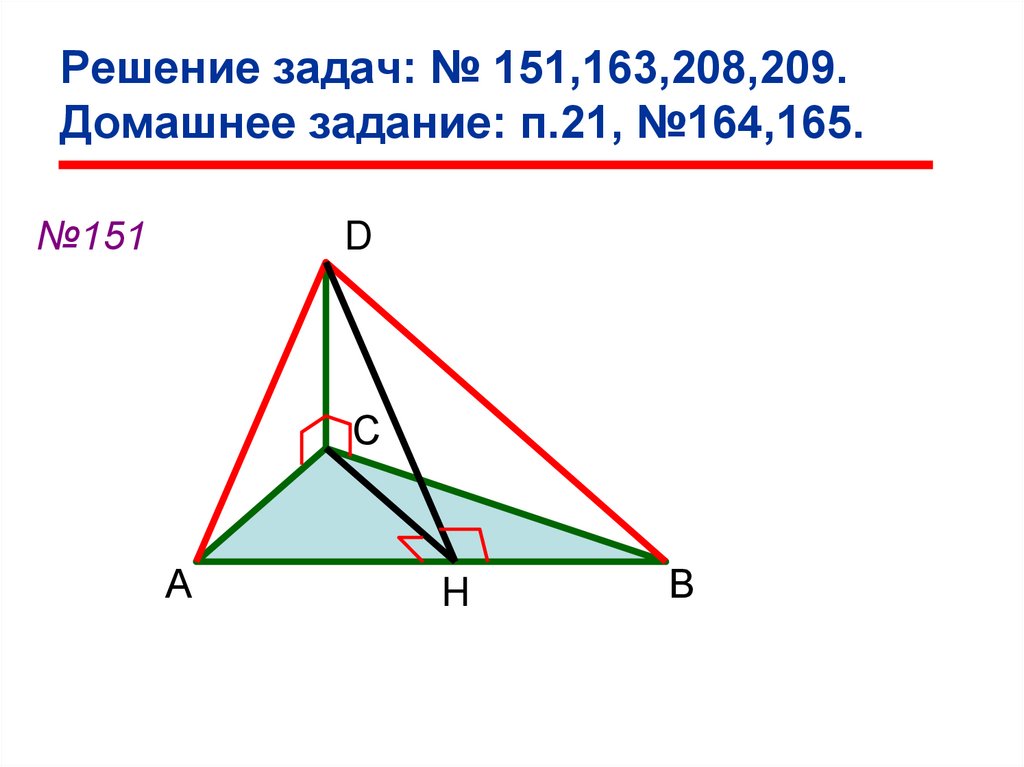
39. Решение задач: № 151,163,208,209. Домашнее задание: п.21, №164,165.

№151
D
С
А
H
В

40.

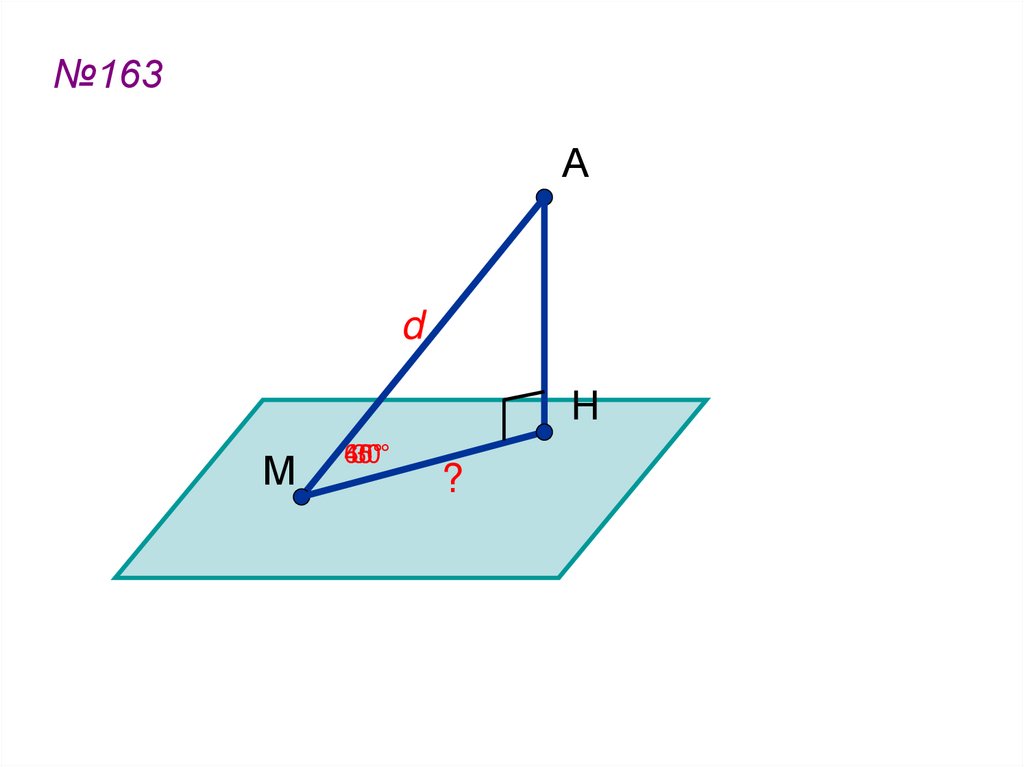
№163
А
d
H
М
45°
60°
30°
?
d 2
a)
;
2
d
б) ;
2
d 3
в)
.
2

41.

Урок 6
Решение задач по теме
«Угол между прямой и
плоскостью»

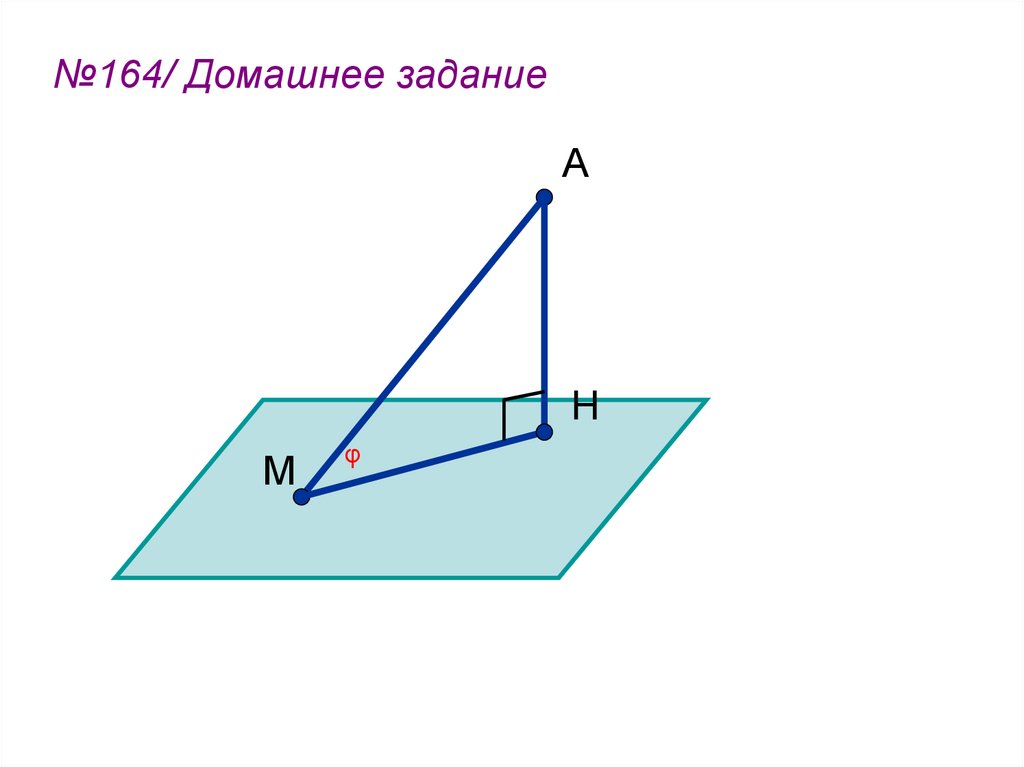
42.

№164/ Домашнее задание
А
H
М
φ
φ = 60°

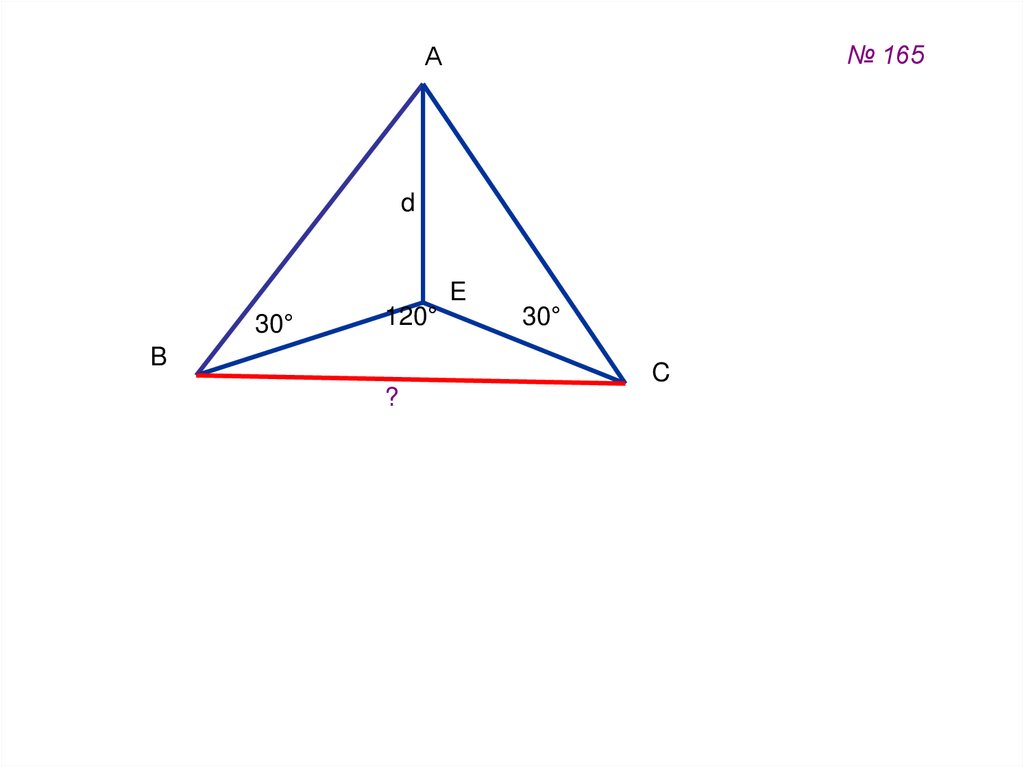
43.

№ 165
А
d
E
120°
30°
30°
B
C
?
BE
tg 60 , BE AEtg60 , ВЕ ВС d 3 ,
AE
2
BC 2 BE 2 BE cos120 2 d 3 2 d 3
2
2 1
2 3d 2 3d 9d 2 ;
2
BC 3d .
2
2
2
cos 60
2

44.

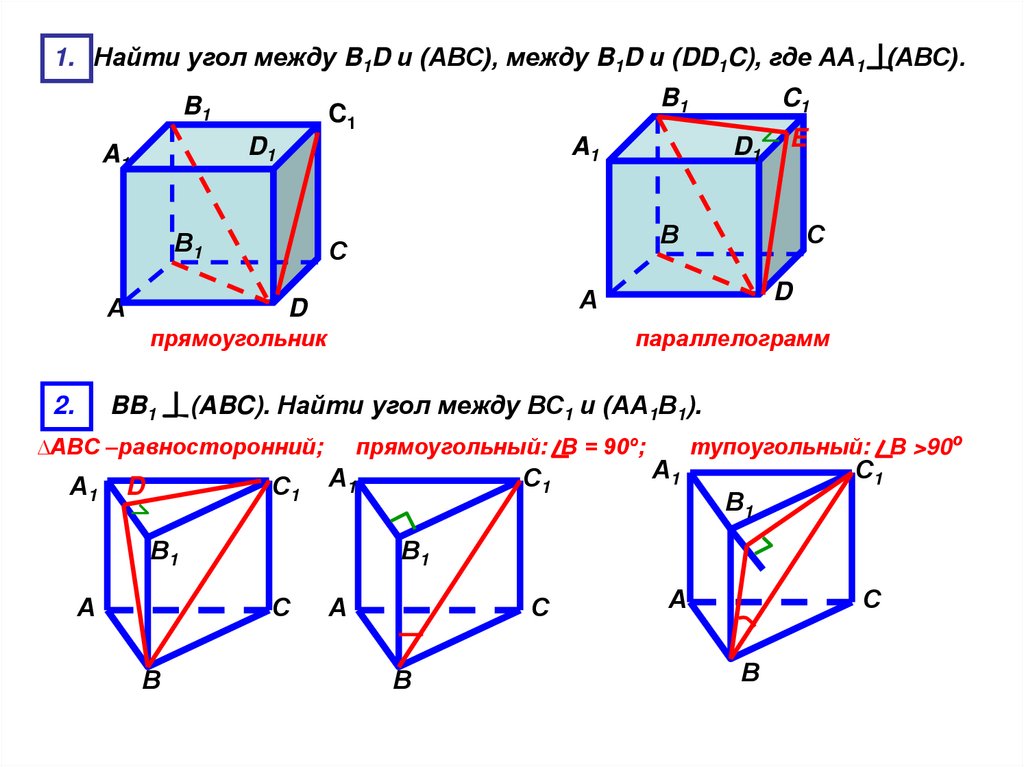
1. Найти угол между B1D и (АВС), между B1D и (DD1C), где АА1 (АВС).
B1
B1
C1
D1
A1
A1
В1
А
параллелограмм
прямоугольный: В = 90º;
А1
В1
А
С1
А1
С
А
тупоугольный: В >90º
В1
С1
В1
С
В
D
(ABC). Найти угол между ВС1 и (АА1В1).
С1
D
С
А
∆АВС –равносторонний;
А1
E
В
D
BB1
D1
С
прямоугольник
2.
C1
А
В
С
В

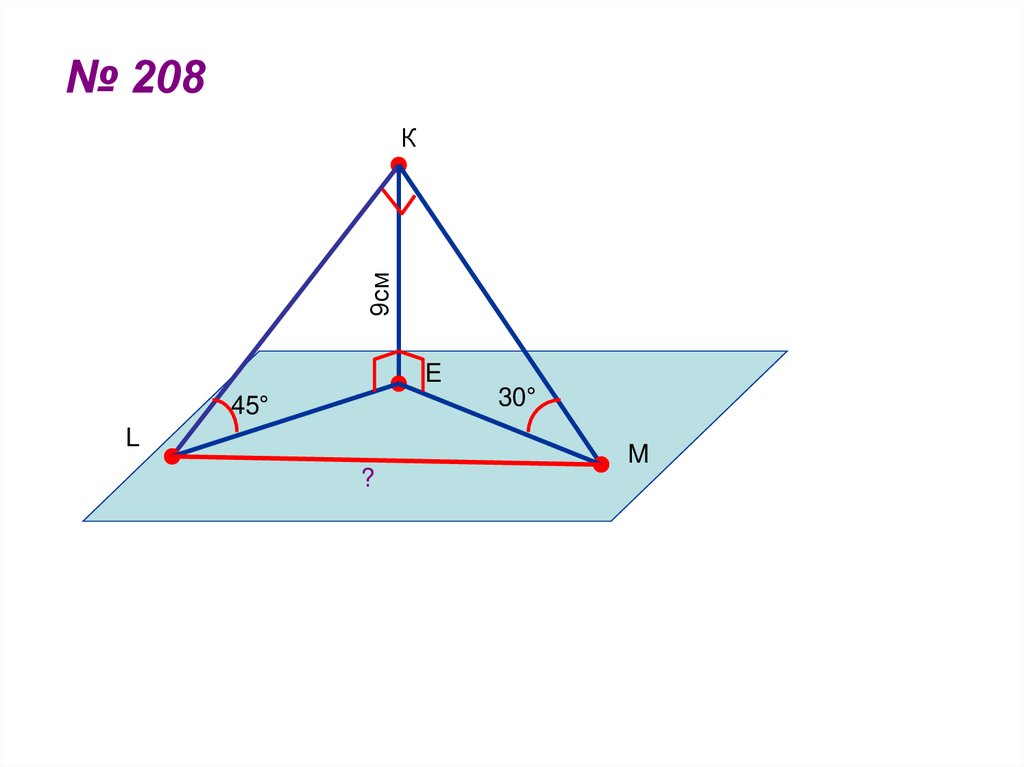
45. № 208

9см
К
E
30°
45°
L
M
?

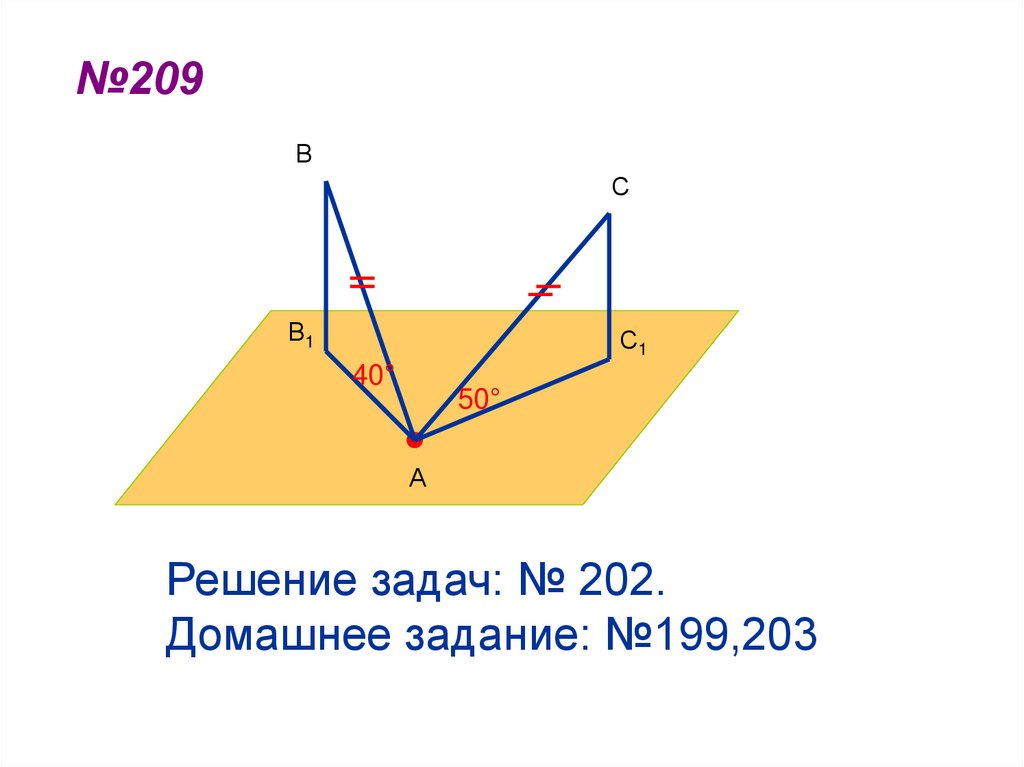
46. №209

В
С
В1
С1
40°
50°
А
Решение задач: № 202.
Домашнее задание: №199,203

47.

Урок 7
Решение задач по темам
§2 «Перпендикуляр и
наклонные. Угол между прямой
и плоскостью»

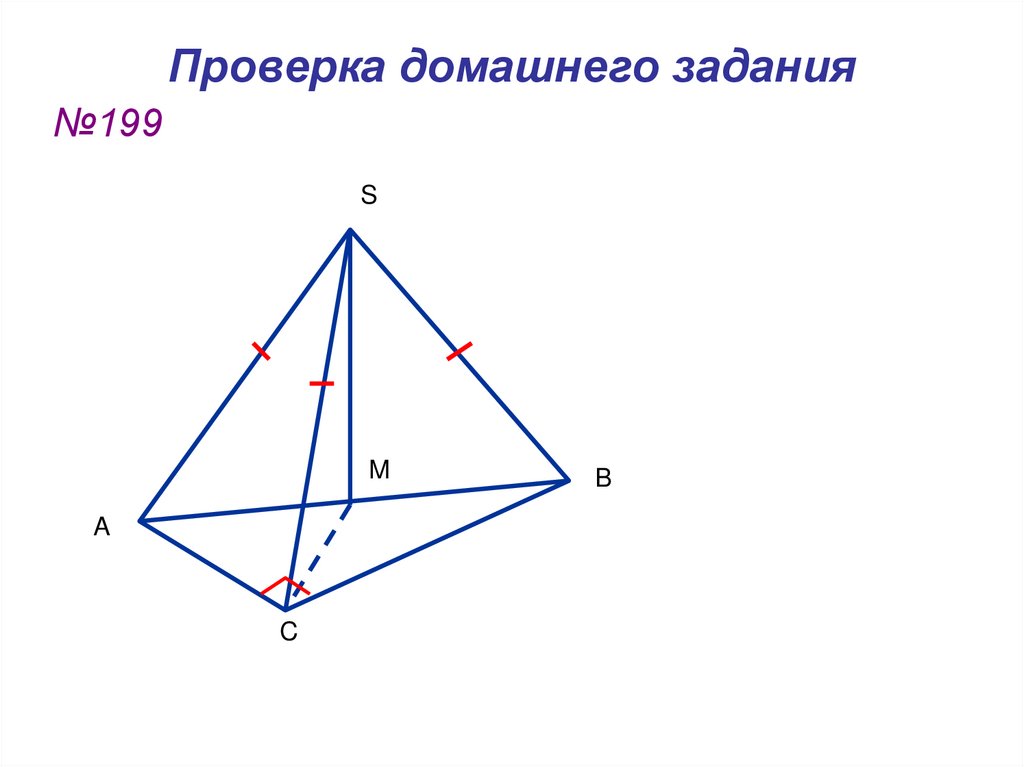
48. Проверка домашнего задания

№199
S
M
A
C
B

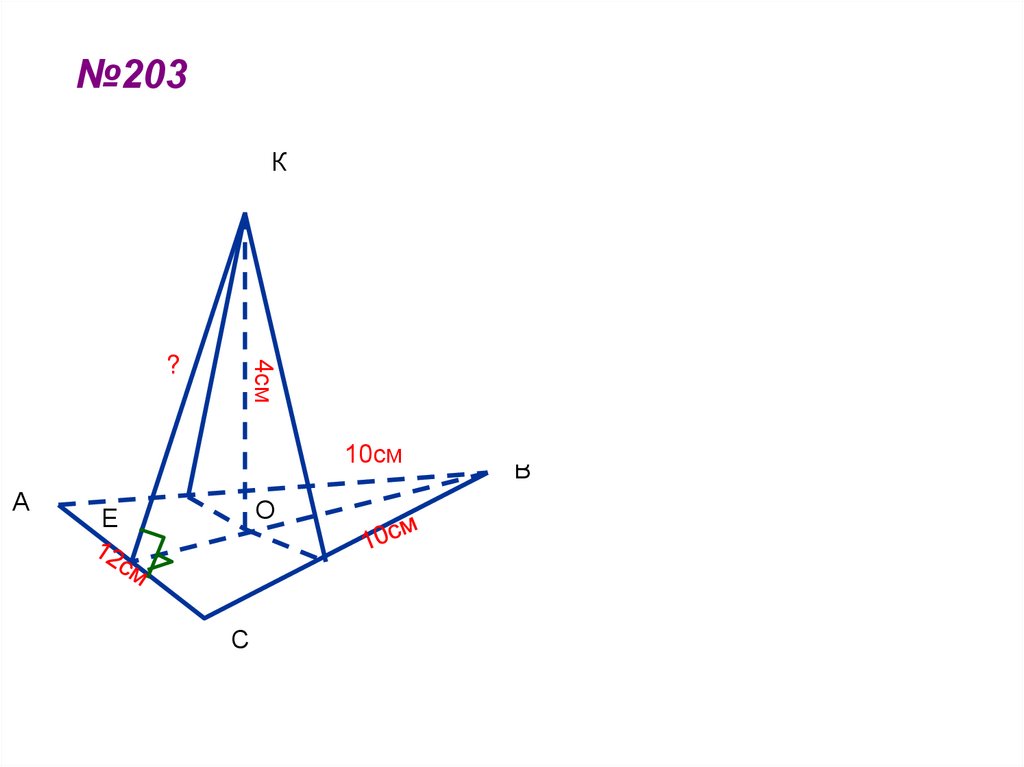
49. №203

2S
ОЕ r
,
P
S p p a p b p c , где
№203
К
4см
?
1
p a b c 16см,
2
S 16 4 6 6 48см 2 ,
ОЕ 96 : 32 3см.
10см
А
О
Е
С
ЕК ОК 2 ОЕ 2 16 9 5см.
В

50.

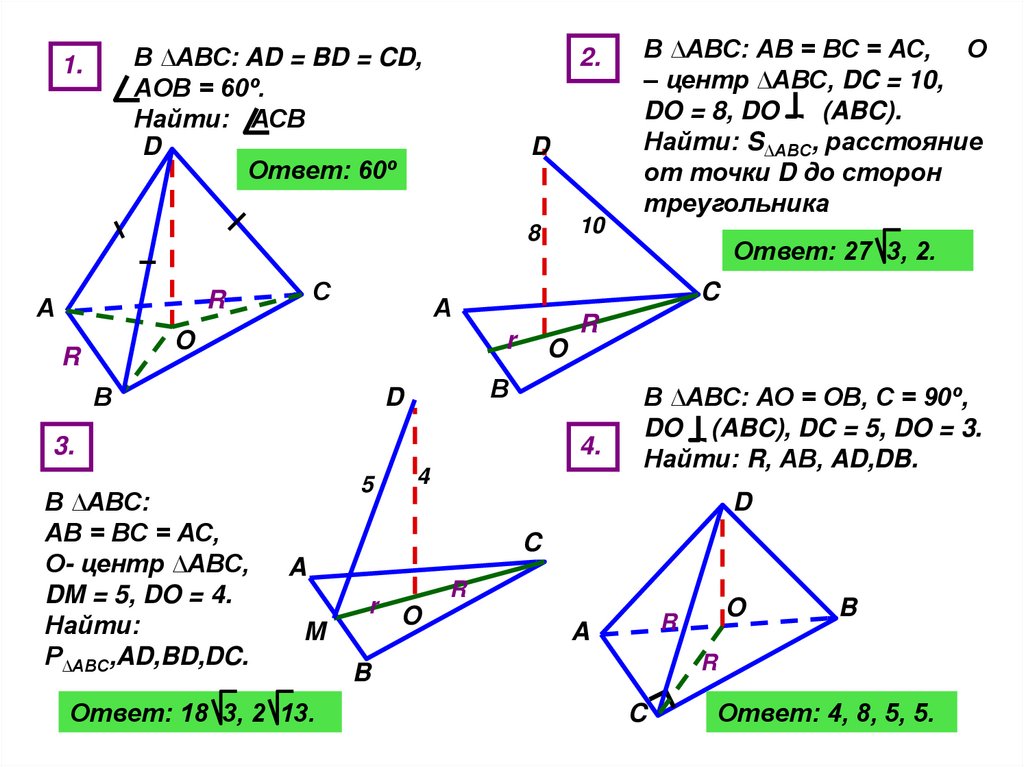
В ∆АВС: AD = BD = CD,
AOB = 60º.
Найти: АСВ
D
Ответ: 60º
1.
2.
D
10
8
С
R
А
R
R
r
В
O
В
D
3.
В ∆АВС:
АВ = ВС = АС,
О- центр ∆АВС,
DM = 5, DO = 4.
Найти:
Р∆АВС,AD,BD,DC.
4.
5
Ответ: 27 3, 2.
C
А
O
В ∆АВС: АВ = ВС = АС, О
– центр ∆АВС, DC = 10,
DO = 8, DO
(ABC).
Найти: S∆ABC, расстояние
от точки D до сторон
треугольника
4
В ∆АВС: АО = ОВ, С = 90º,
DO (ABC), DC = 5, DO = 3.
Найти: R, АВ, AD,DB.
D
C
A
r
M
Ответ: 18 3, 2 13.
R
O
O
R
A
B
R
B
C
Ответ: 4, 8, 5, 5.

51.

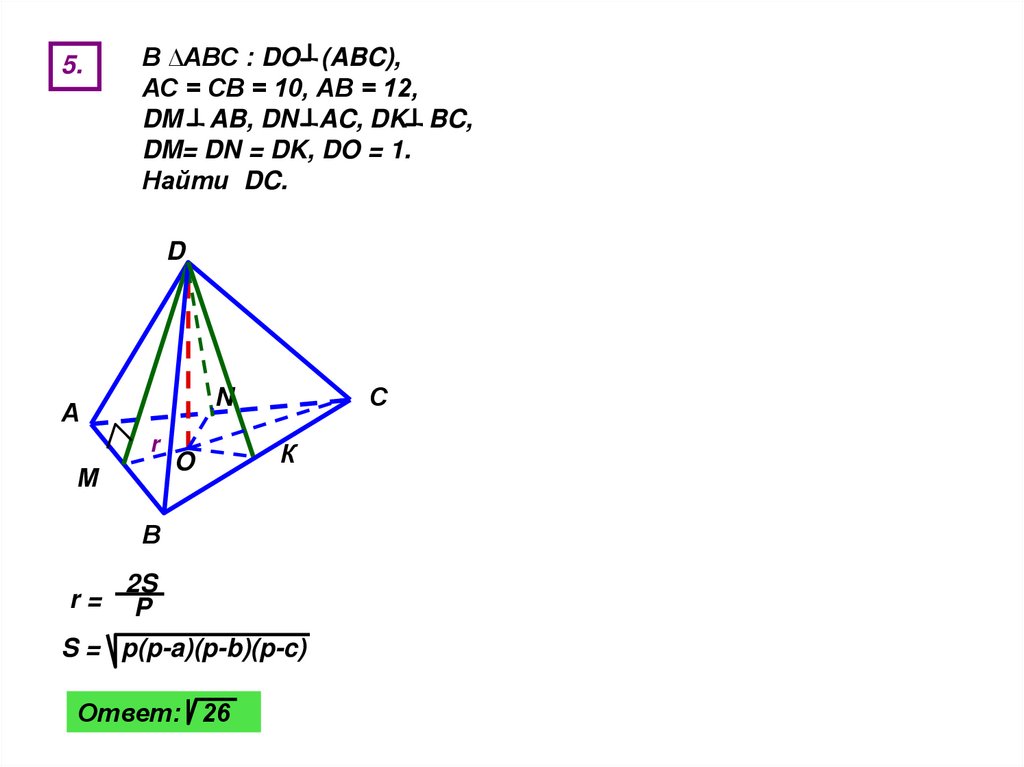
5.
В ∆АВС : DO (ABC),
АС = СВ = 10, АВ = 12,
DM AB, DN AC, DK BC,
DM= DN = DK, DO = 1.
Найти DC.
D
С
N
А
r
М
O
К
В
r=
2S
P
S = p(p-a)(p-b)(p-c)
Ответ: 26

52. Решение задач: №202,204. Домашнее задание: №206,207.

53.

54.

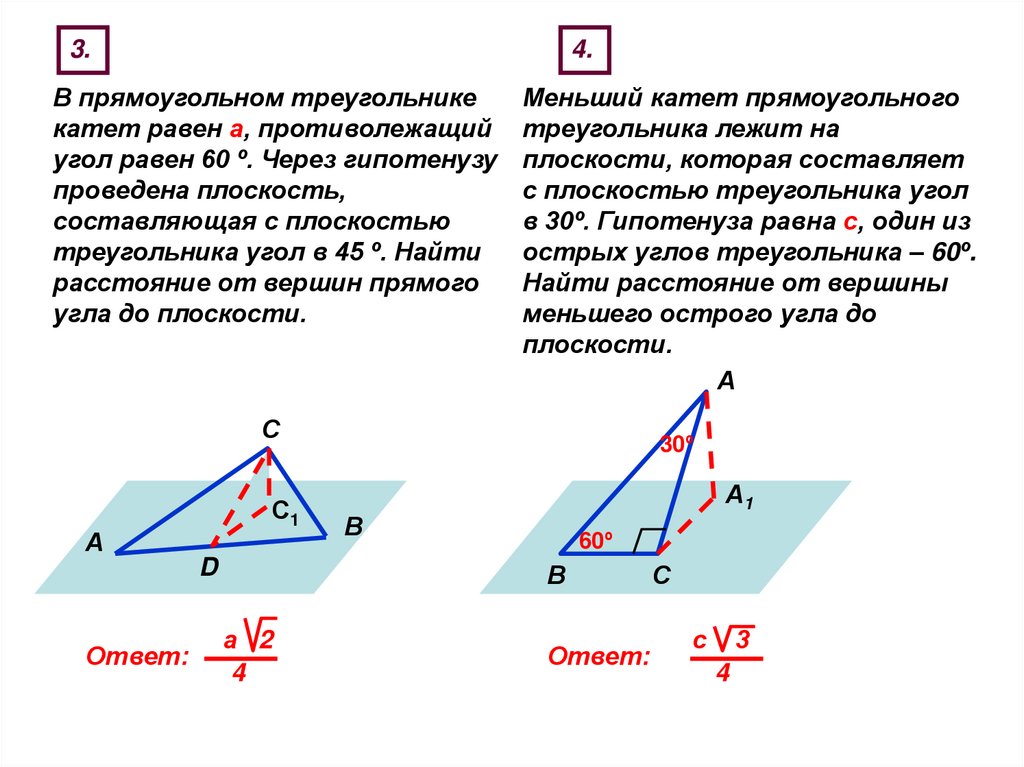
3.
4.
В прямоугольном треугольнике
катет равен а, противолежащий
угол равен 60 º. Через гипотенузу
проведена плоскость,
составляющая с плоскостью
треугольника угол в 45 º. Найти
расстояние от вершин прямого
угла до плоскости.
Меньший катет прямоугольного
треугольника лежит на
плоскости, которая составляет
с плоскостью треугольника угол
в 30º. Гипотенуза равна с, один из
острых углов треугольника – 60º.
Найти расстояние от вершины
меньшего острого угла до
плоскости.
А
С
С1
А
D
Ответ:
30º
А1
В
60º
В
а 2
4
Ответ:
С
с
3
4

55.

56.

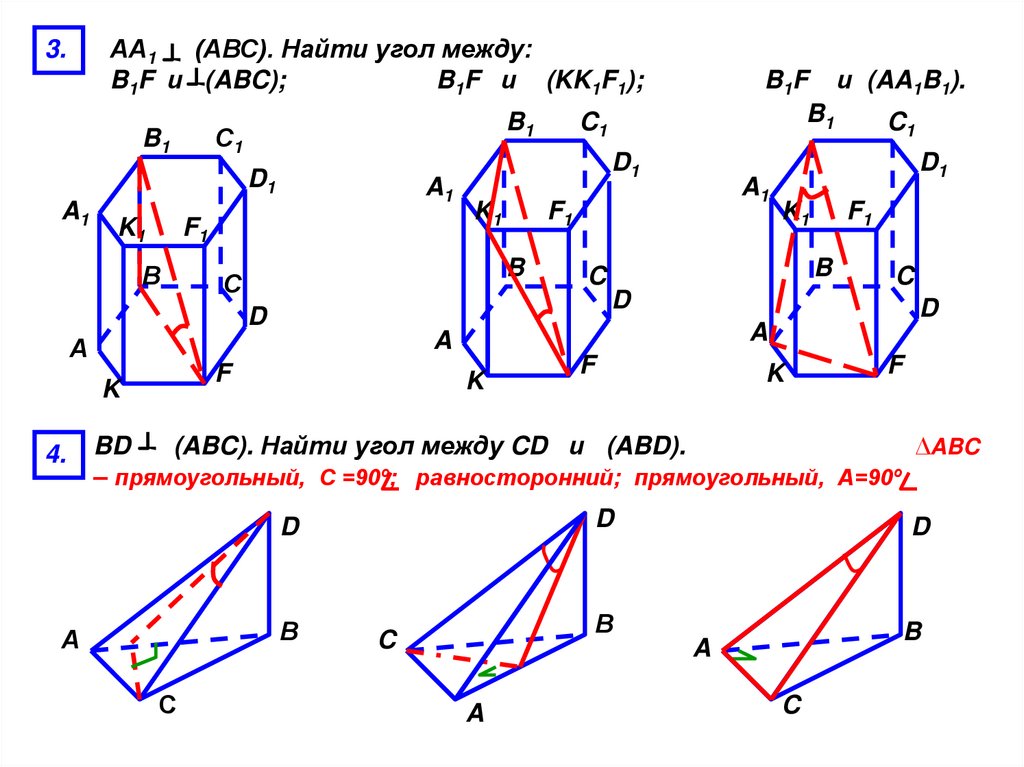
АА1
(АВС). Найти угол между:
B1F и (ABC);
B1F и (KK1F1);
3.
B1
С1
B1
D1
A1
K1
A1
F1
В
C1
1
D1
K1
B
С
A1
F1
K1
F1
B
C
D
D
A
A
А
F
K
D1
C
D
4.
B1F и (AA1B1).
B1
C
K
F
K
F
BD
(ABC). Найти угол между CD и (ABD).
∆ABC
– прямоугольный, С =90º; равносторонний; прямоугольный, А=90º
D
D
В
А
С
D
В
C
B
A
A
C

57.

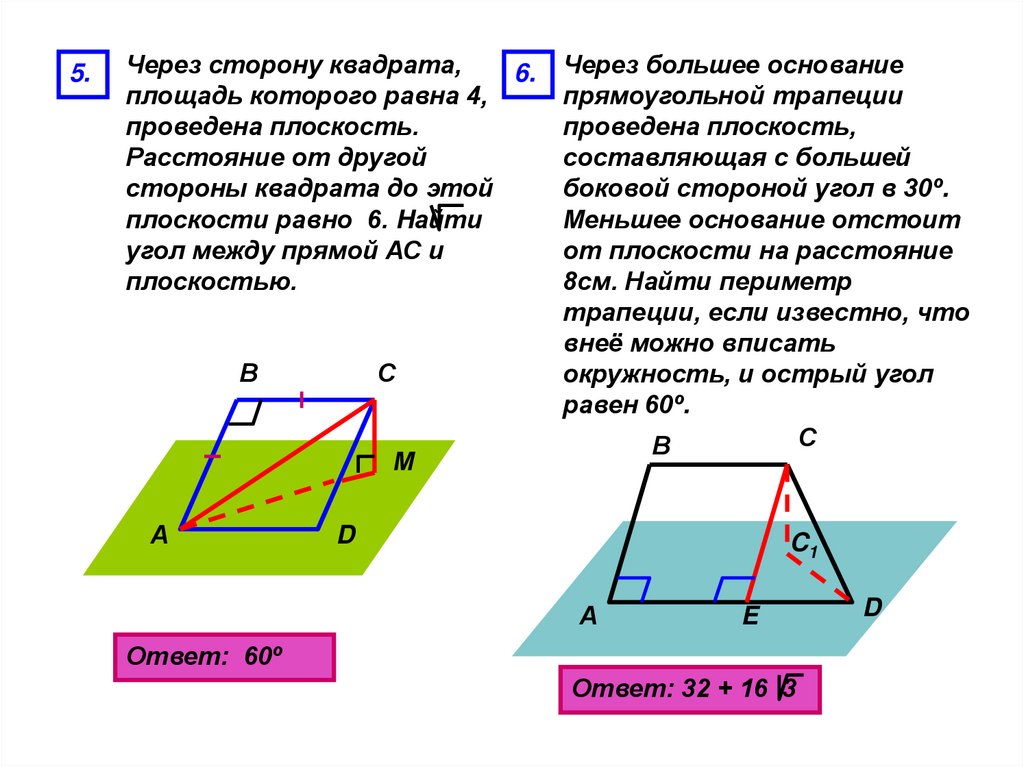
5.
Через сторону квадрата,
6.
площадь которого равна 4,
проведена плоскость.
Расстояние от другой
стороны квадрата до этой
плоскости равно 6. Hайти
угол между прямой АС и
плоскостью.
В
С
М
А
Через большее основание
прямоугольной трапеции
проведена плоскость,
составляющая с большей
боковой стороной угол в 30º.
Меньшее основание отстоит
от плоскости на расстояние
8см. Найти периметр
трапеции, если известно, что
внеё можно вписать
окружность, и острый угол
равен 60º.
С
В
D
C1
А
E
Ответ: 60º
Ответ: 32 + 16 3
D