Similar presentations:
Перпендикулярность прямой и плоскости. Занятие №24
1.
Перпендикулярностьпрямой и плоскости
Занятие №24
2.
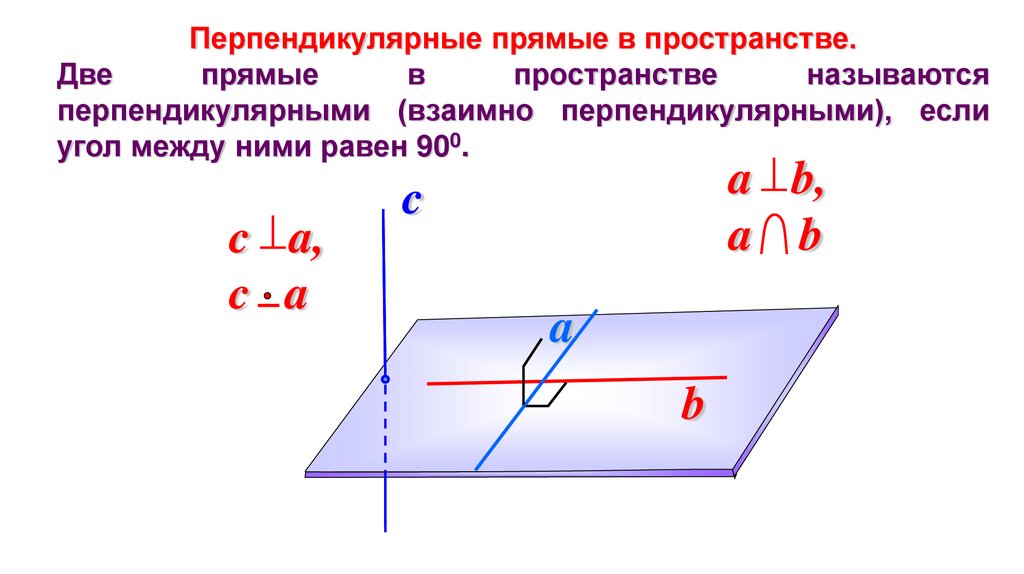
Перпендикулярные прямые в пространстве.Две
прямые
в
пространстве
называются
перпендикулярными (взаимно перпендикулярными), если
угол между ними равен 900.
c a,
c a
a b,
a b
c
a
b
3.
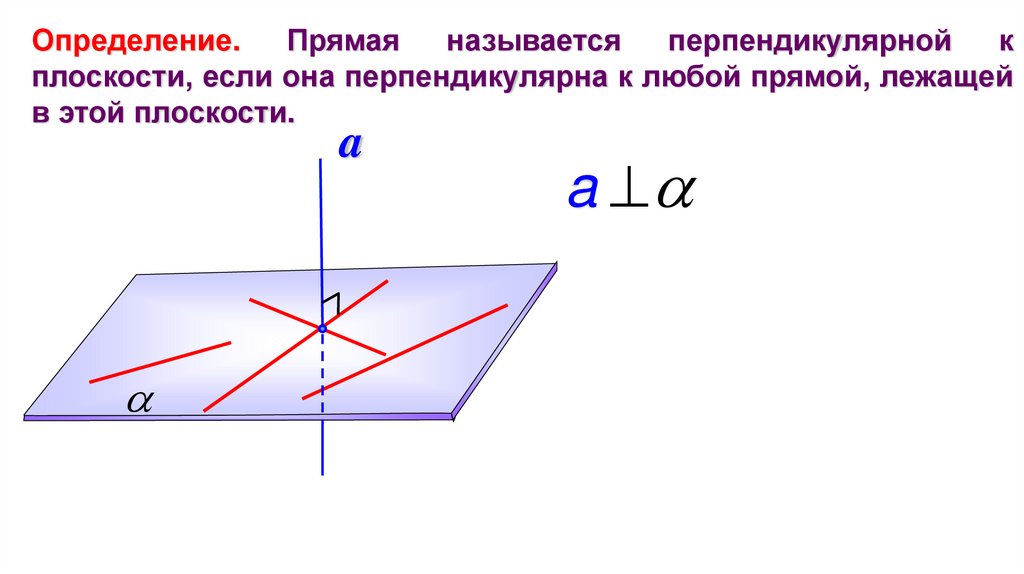
Определение.Прямая
называется
перпендикулярной
к
плоскости, если она перпендикулярна к любой прямой, лежащей
в этой плоскости.
a
a
4.
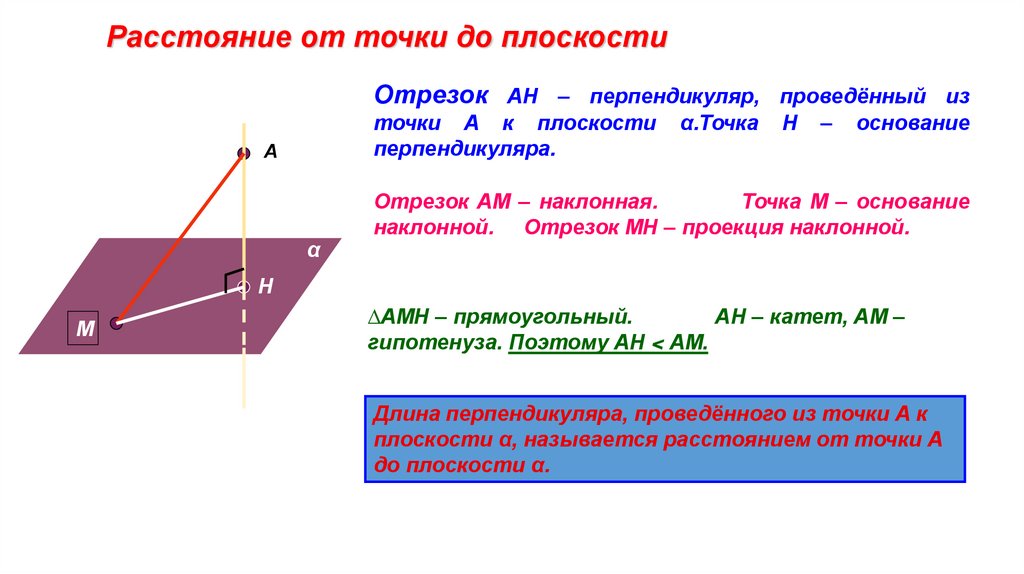
Расстояние от точки до плоскостиОтрезок АН – перпендикуляр, проведённый из
точки А к плоскости
перпендикуляра.
А
α
α.Точка
Н
–
основание
Отрезок АМ – наклонная.
Точка М – основание
наклонной. Отрезок МН – проекция наклонной.
Н
М
∆АМН – прямоугольный.
АН – катет, АМ –
гипотенуза. Поэтому АН < АМ.
Длина перпендикуляра, проведённого из точки А к
плоскости α, называется расстоянием от точки А
до плоскости α.
5.
Свойство наклонных и их проекций: Если из некоторой точкипроведены к плоскости две наклонные, то: 1) если наклонные равны, то
равны и их проекции; 2) если проекции наклонных равны, то равны и
наклонные.
Важная задача: Если точка равноудалена от всех
вершин
n - угольника, то она проецируется в
центр описанной около n - угольника окружности.
М
С
А
O
В
Верно и обратное утверждение: Если точка лежит на
перпендикуляре, проходящем через центр описанной около
многоугольника окружности, то она равноудалена от вершин
этого многоугольника
6.
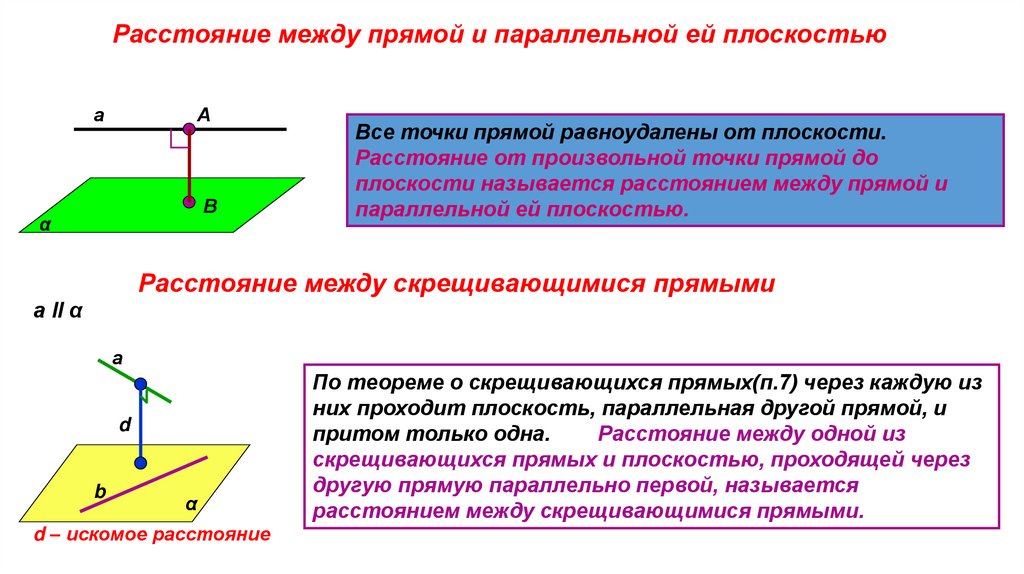
Расстояние между прямой и параллельной ей плоскостьюа
А
В
α
Все точки прямой равноудалены от плоскости.
Расстояние от произвольной точки прямой до
плоскости называется расстоянием между прямой и
параллельной ей плоскостью.
Расстояние между скрещивающимися прямыми
а ll α
а
d
b
α
d – искомое расстояние
По теореме о скрещивающихся прямых(п.7) через каждую из
них проходит плоскость, параллельная другой прямой, и
притом только одна.
Расстояние между одной из
скрещивающихся прямых и плоскостью, проходящей через
другую прямую параллельно первой, называется
расстоянием между скрещивающимися прямыми.
7.
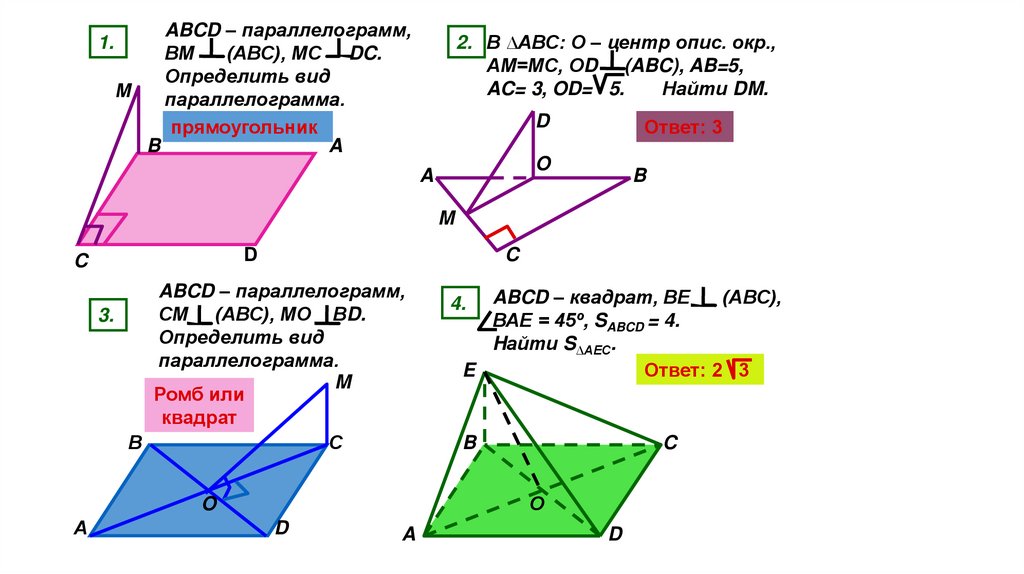
ABCD – параллелограмм,ВМ
(АВС), МС DC.
Определить вид
параллелограмма.
1.
М
2. В ∆АВС: О – центр опис. окр.,
АМ=МС, ОD (ABC), AB=5,
AC= 3, OD= 5.
Найти DM.
D
B
A
O
A
B
M
D
C
C
ABCD – параллелограмм,
СМ (АВС), МО ВD.
Определить вид
параллелограмма.
M
3.
В
С
ABCD – квадрат, ВЕ
ВАЕ = 45º, SABCD = 4.
Hайти S∆AEC.
E
B
C
О
O
А
4.
D
A
D
(АВС),
8.
1.ABCD – параллелограмм,
ВМ
(АВС), МС DC.
Определить вид
М
параллелограмма.
прямоугольник
B
A
2. В ∆АВС: О – центр опис. окр.,
АМ=МС, ОD (ABC), AB=5,
AC= 3, OD= 5.
Найти DM.
D
Ответ: 3
O
A
B
M
D
C
C
ABCD – параллелограмм,
СМ (АВС), МО ВD.
3.
Определить вид
параллелограмма.
M
Ромб или
квадрат
В
С
B
C
О
O
А
ABCD – квадрат, ВЕ
(АВС),
ВАЕ = 45º, SABCD = 4.
Hайти S∆AEC.
E
Ответ: 2 3
4.
D
A
D
9.
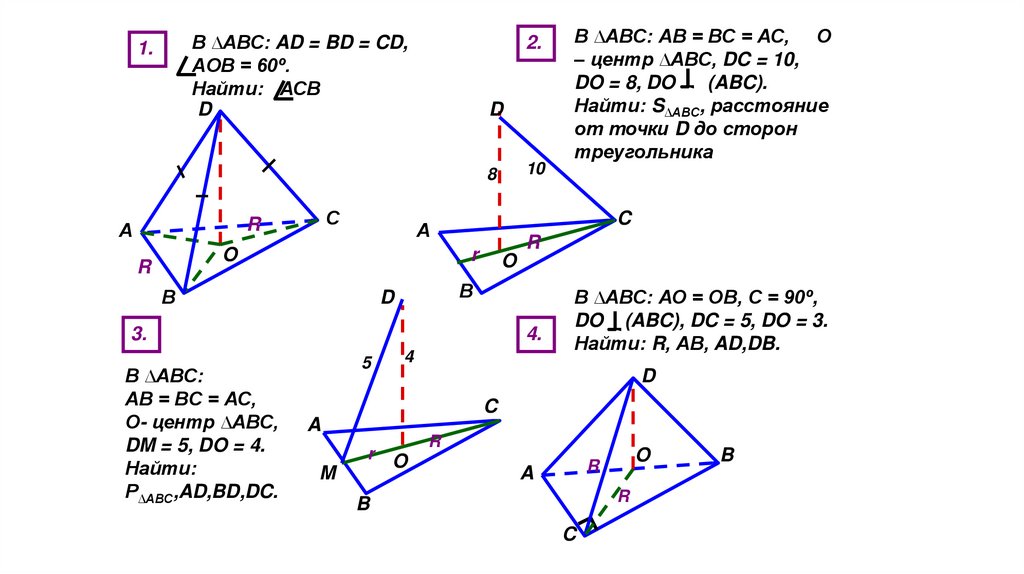
В ∆АВС: AD = BD = CD,AOB = 60º.
Найти: АСВ
D
1.
2.
D
10
8
С
R
А
R
C
А
O
R
r
В
O
В
D
3.
В ∆АВС:
АВ = ВС = АС,
О- центр ∆АВС,
DM = 5, DO = 4.
Найти:
Р∆АВС,AD,BD,DC.
4.
5
В ∆АВС: АВ = ВС = АС, О
– центр ∆АВС, DC = 10,
DO = 8, DO
(ABC).
Найти: S∆ABC, расстояние
от точки D до сторон
треугольника
4
В ∆АВС: АО = ОВ, С = 90º,
DO (ABC), DC = 5, DO = 3.
Найти: R, АВ, AD,DB.
D
C
A
r
M
R
O
O
R
A
R
B
C
B
10.
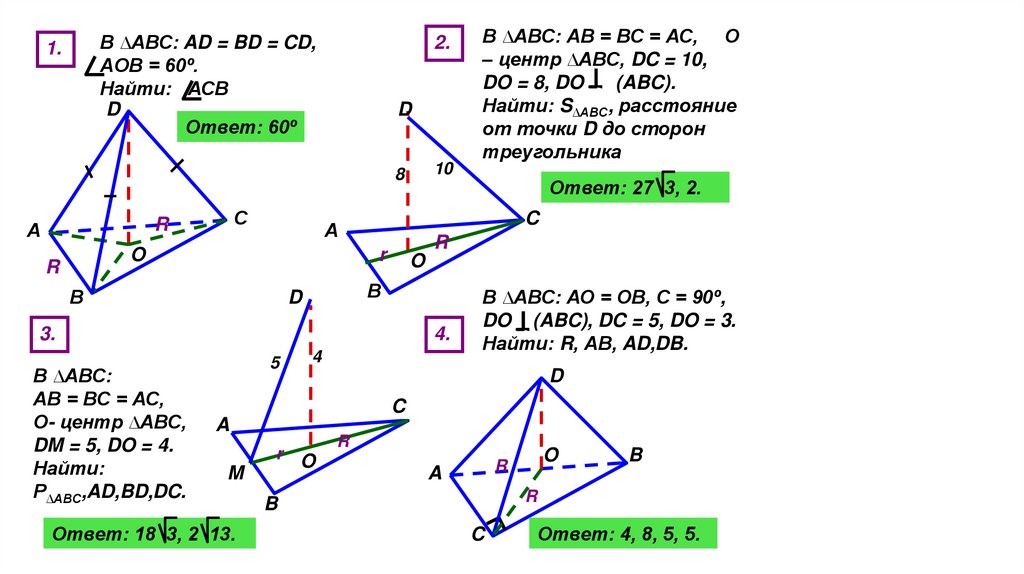
В ∆АВС: AD = BD = CD,AOB = 60º.
Найти: АСВ
D
Ответ: 60º
1.
2.
D
10
8
С
R
А
R
R
r
В
O
В
D
3.
В ∆АВС:
АВ = ВС = АС,
О- центр ∆АВС,
DM = 5, DO = 4.
Найти:
Р∆АВС,AD,BD,DC.
4.
5
Ответ: 27 3, 2.
C
А
O
В ∆АВС: АВ = ВС = АС, О
– центр ∆АВС, DC = 10,
DO = 8, DO
(ABC).
Найти: S∆ABC, расстояние
от точки D до сторон
треугольника
4
В ∆АВС: АО = ОВ, С = 90º,
DO (ABC), DC = 5, DO = 3.
Найти: R, АВ, AD,DB.
D
C
A
r
M
Ответ: 18 3, 2 13.
R
O
O
R
A
B
R
B
C
Ответ: 4, 8, 5, 5.
11.
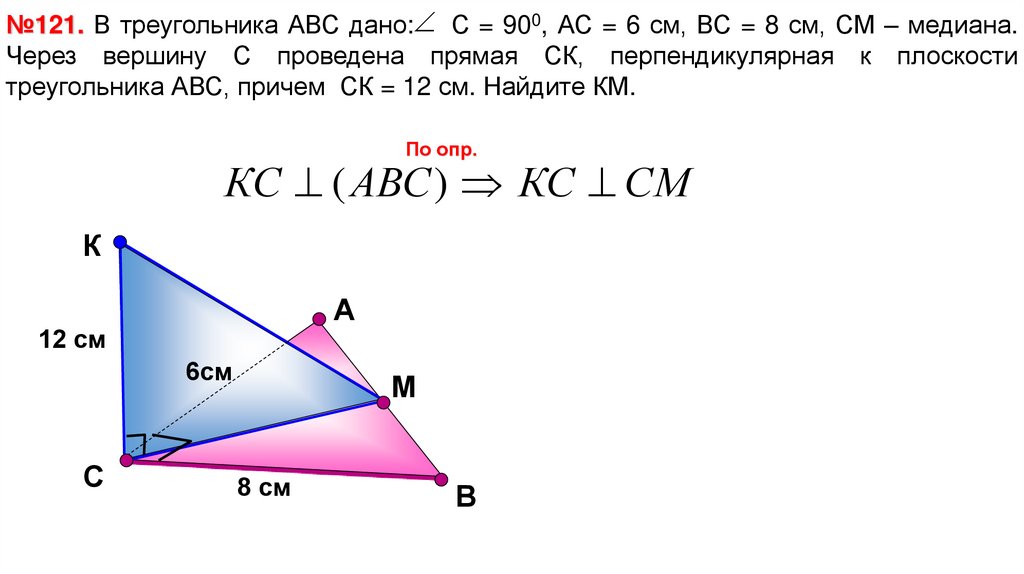
№121. В треугольника АВС дано: С = 900, АС = 6 см, ВС = 8 см, СМ – медиана.Через вершину С проведена прямая СК, перпендикулярная к плоскости
треугольника АВС, причем СК = 12 см. Найдите КМ.
По опр.
КС ( АВС ) КС СМ
К
А
12 см
6см
С
М
8 см
В
12.
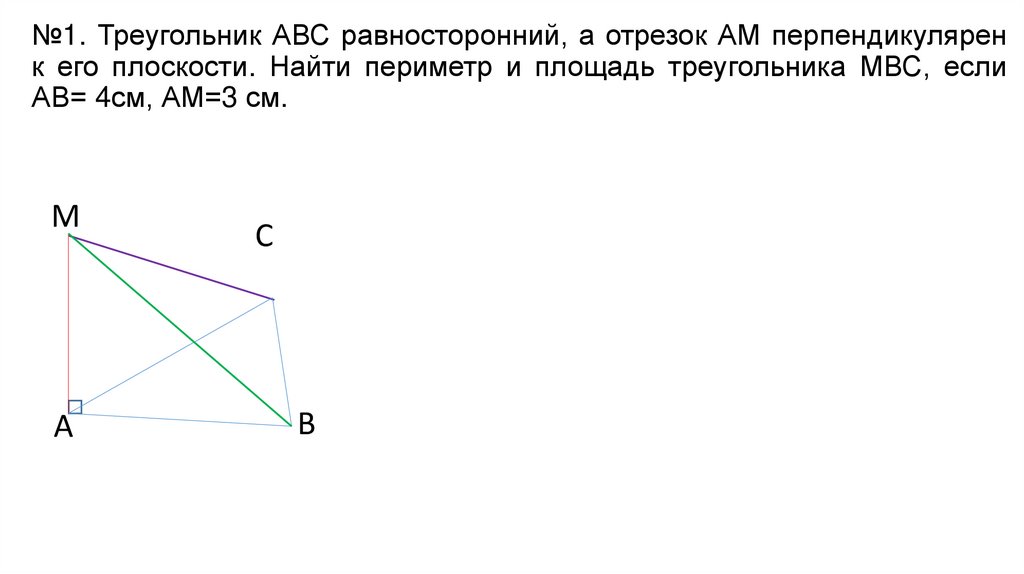
№1. Треугольник АВС равносторонний, а отрезок АМ перпендикуляренк его плоскости. Найти периметр и площадь треугольника МВС, если
АВ= 4см, АМ=3 см.
M
A
C
B
13.
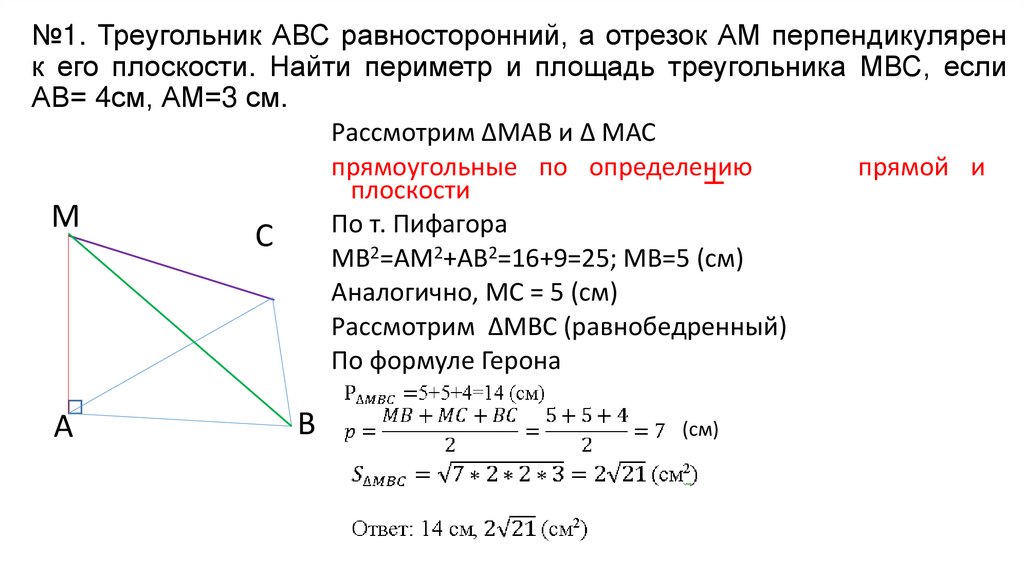
№1. Треугольник АВС равносторонний, а отрезок АМ перпендикуляренк его плоскости. Найти периметр и площадь треугольника МВС, если
АВ= 4см, АМ=3 см.
Рассмотрим ΔМАВ и Δ МАС
прямоугольные по определению
прямой и
плоскости
M
По т. Пифагора
C
МВ2=АМ2+АВ2=16+9=25; МВ=5 (см)
Аналогично, МС = 5 (см)
Рассмотрим ΔМВС (равнобедренный)
По формуле Герона
A
B
(cм)
14.
№2. Из точки S к плоскости проведены три наклонные, длинной25 см, 30 см и 40 см. Найти проекцию третей наклонной на эту
плоскость, если разность проекции двух наклонных равна 11 см.
S
A
O
B
C
15.
№2. Из точки S к плоскости проведены три наклонные, длинной25 см, 30 см и 40 см. Найти проекцию третей наклонной на эту
плоскость, если разность проекции двух наклонных равна 11 см.
Пусть ОА= х см, тогда ОВ= х+11 см.
Из ΔSOA и ΔSOВ по теореме Пифагора:
SO2=SА2-АО2 и SO2=SВ2-ВО2, или
625-х2=900-(х+11)2
Отсюда х=7.Тогда АО=7 см, а ВО= 18 см.
S
A
O
B
C





 mathematics
mathematics








