Similar presentations:
Перпендикулярность прямых и плоскостей
1. «Перпендикулярность прямых и плоскостей»
Обобщающий урок2.
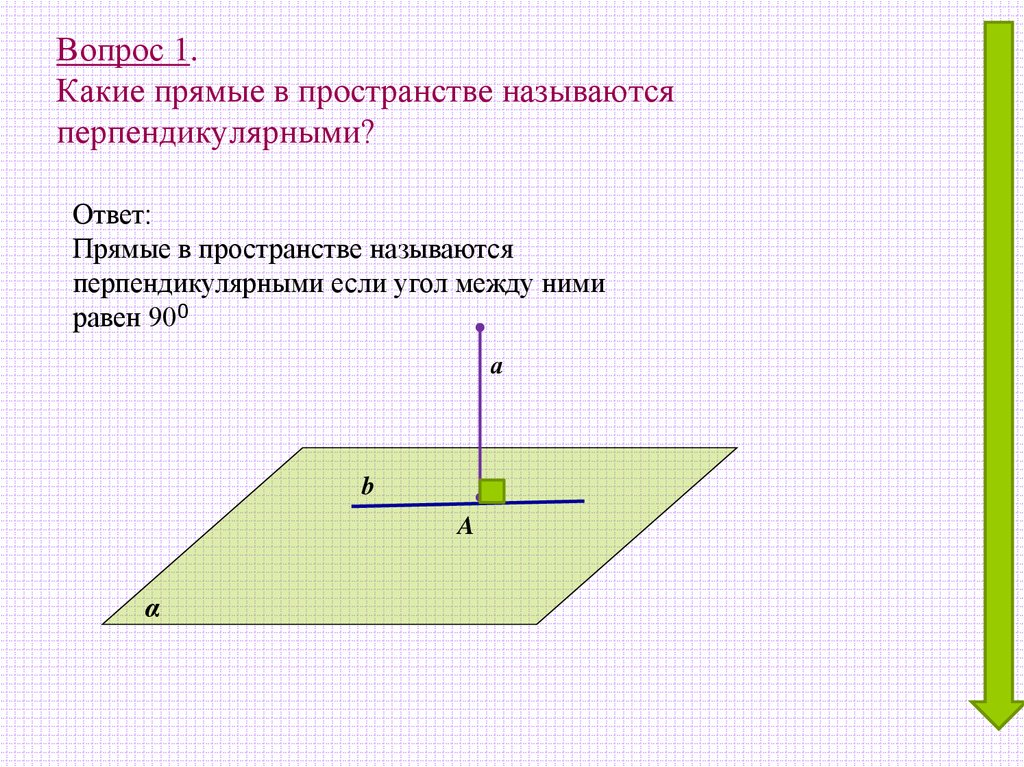
Вопрос 1.Какие прямые в пространстве называются
перпендикулярными?
Ответ:
Прямые в пространстве называются
перпендикулярными если угол между ними
равен 900
а
b
A
α
3.
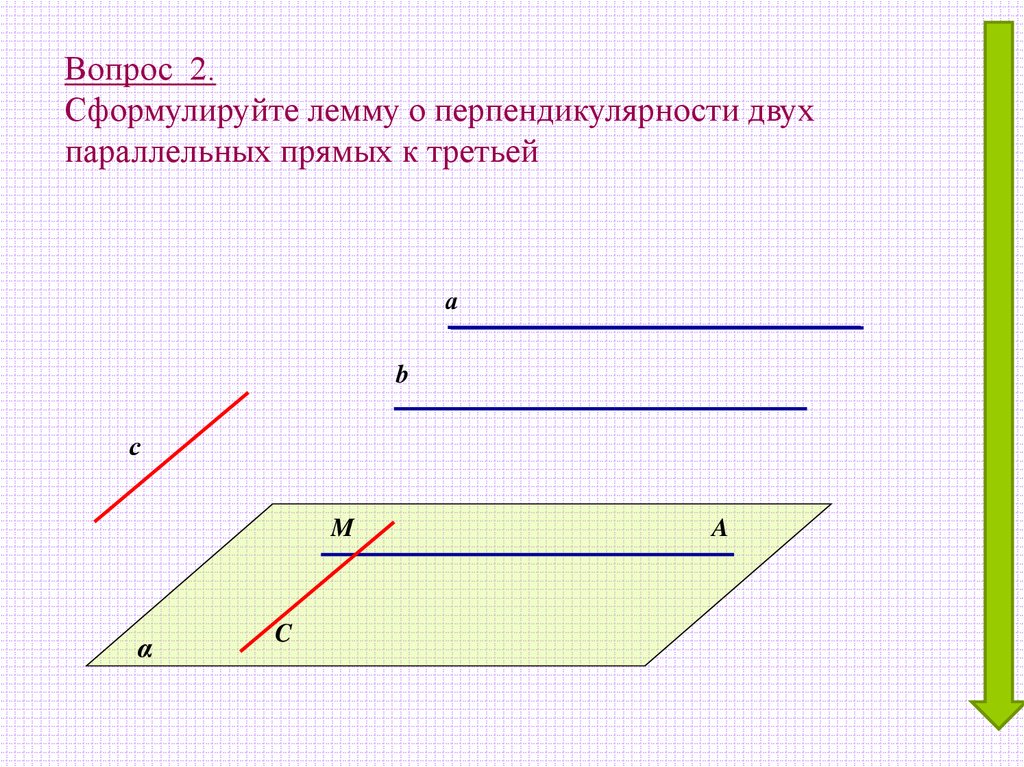
Вопрос 2.Сформулируйте лемму о перпендикулярности двух
параллельных прямых к третьей
а
b
с
M
α
C
A
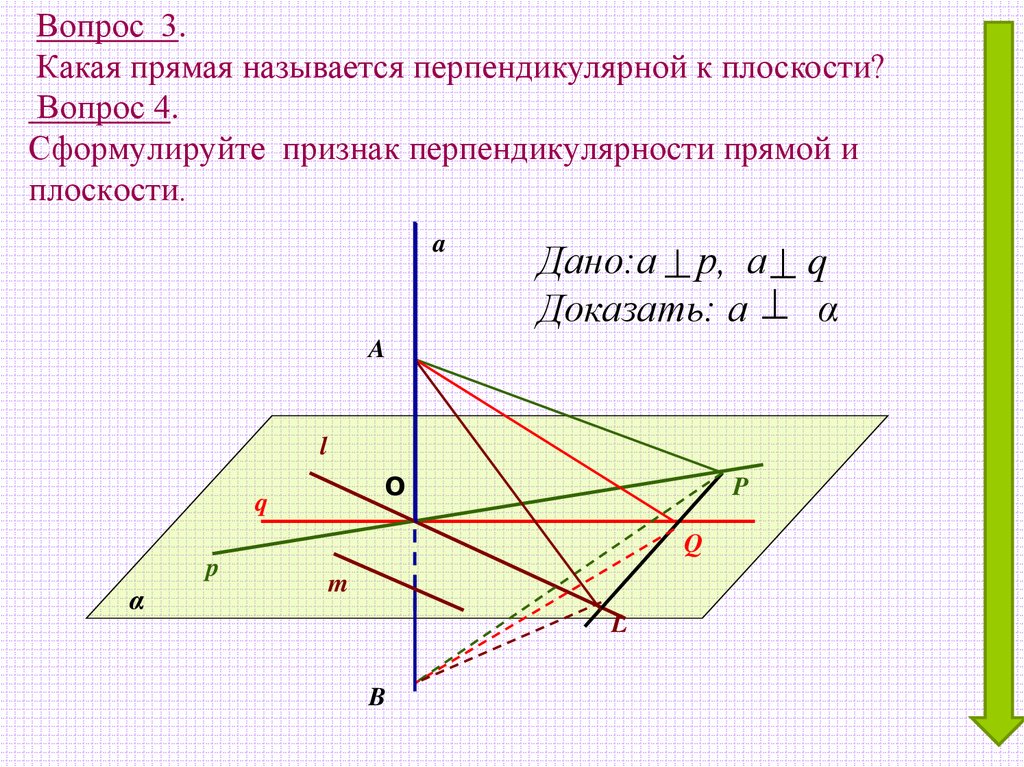
4. Вопрос 4. Сформулируйте признак перпендикулярности прямой и плоскости.
Вопрос 3.Какая прямая называется перпендикулярной к плоскости?
Вопрос 4.
Сформулируйте признак перпендикулярности прямой и
плоскости.
a
Дано:а р, а q
Доказать: а α
A
l
O
q
P
Q
p
α
m
L
B
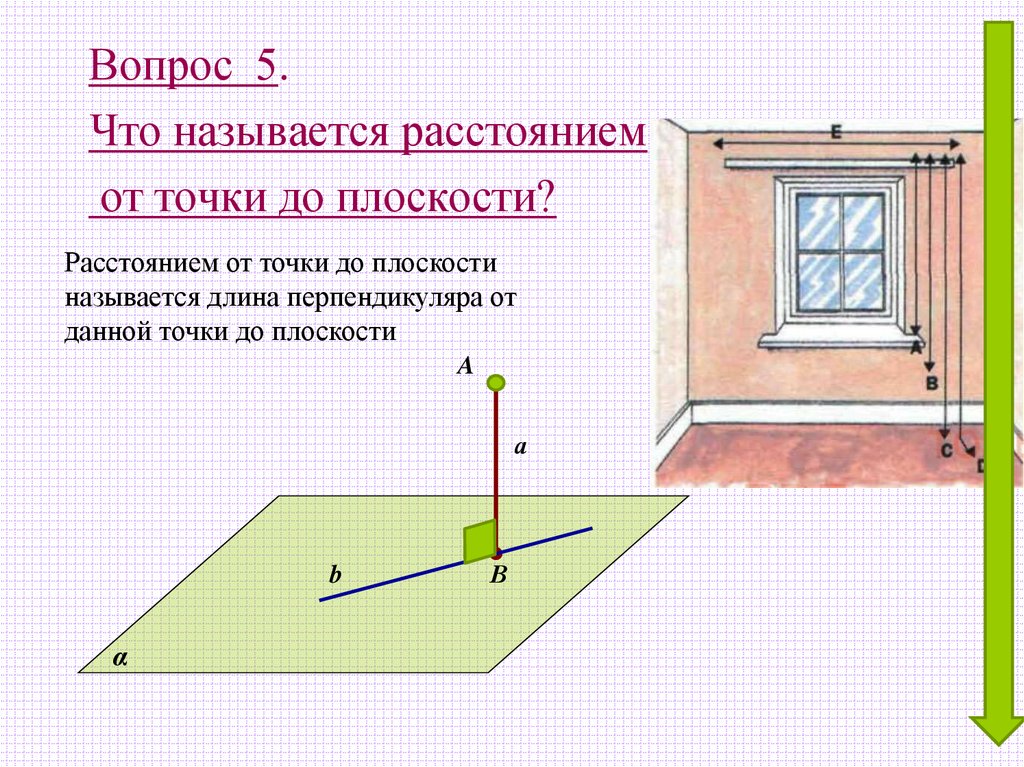
5.
Вопрос 5.Что называется расстоянием
от точки до плоскости?
Расстоянием от точки до плоскости
называется длина перпендикуляра от
данной точки до плоскости
A
а
b
α
В
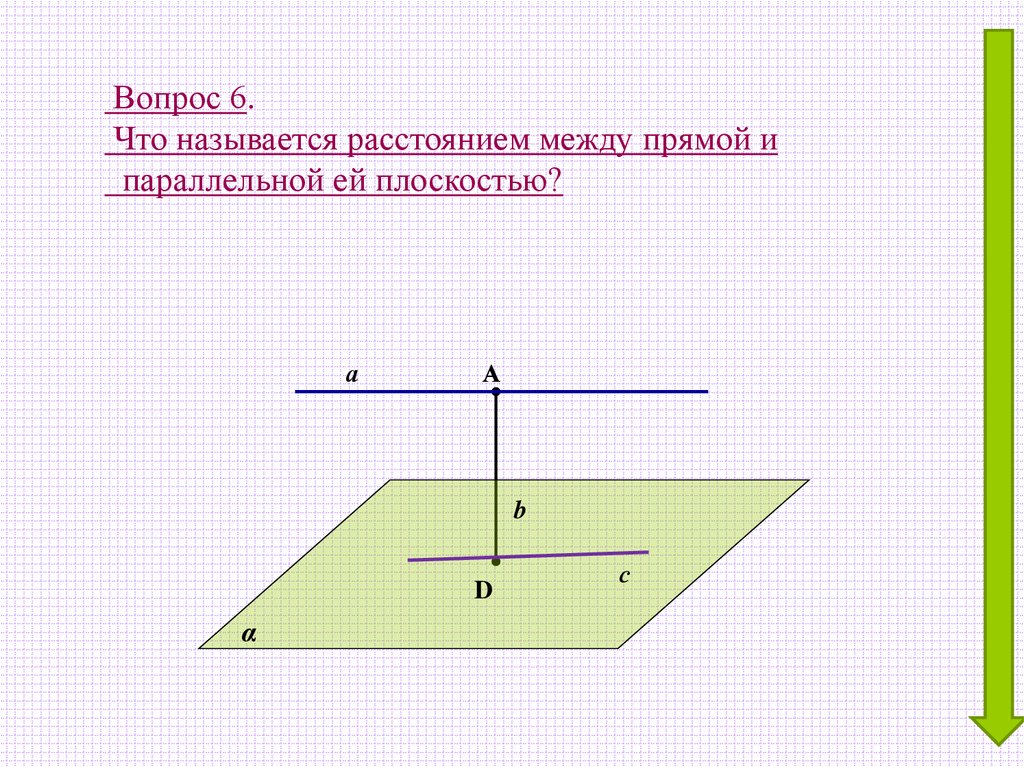
6.
Вопрос 6.Что называется расстоянием между прямой и
параллельной ей плоскостью?
а
А
b
D
α
с
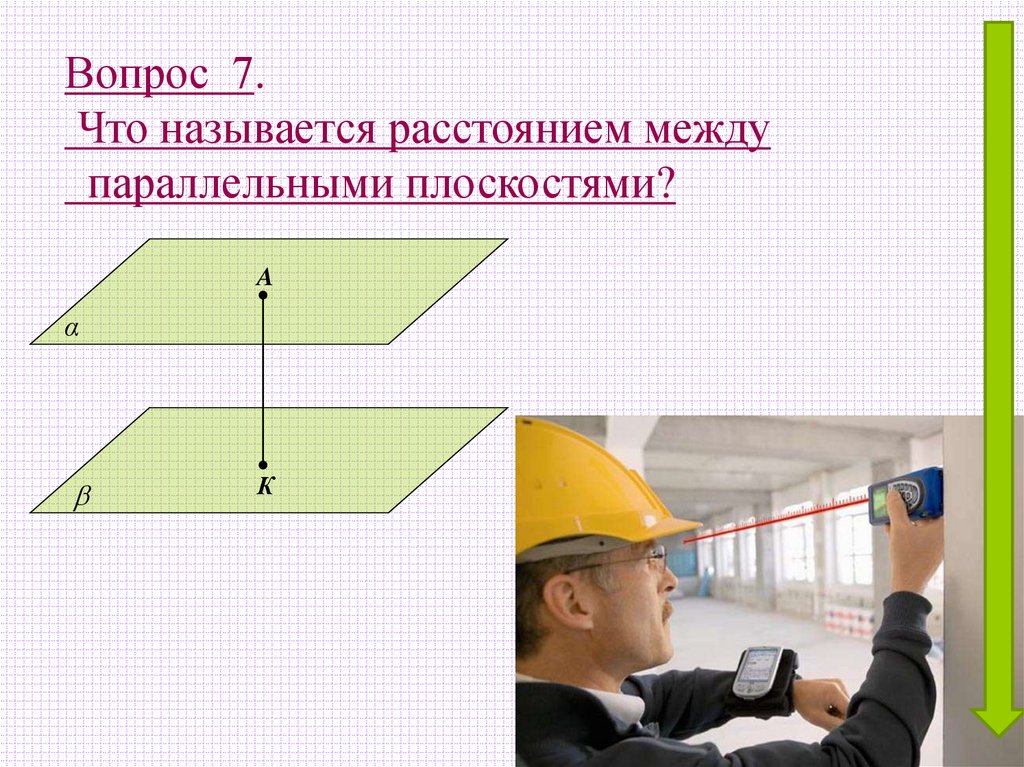
7.
Вопрос 7.Что называется расстоянием между
параллельными плоскостями?
A
α
К
8.
Вопрос 8.Какие прямые называются скрещивающимися?
α
b
а
Ответ: Скрещивающимися
называются прямые, которые не
лежат в одной плоскости
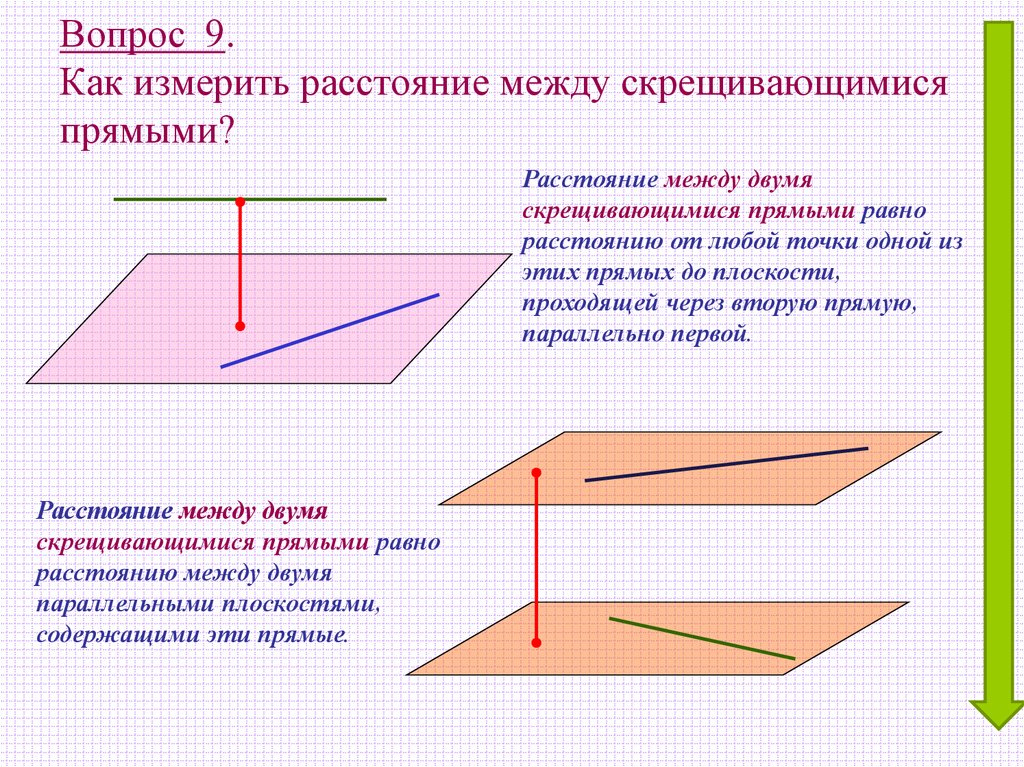
9. Вопрос 9. Как измерить расстояние между скрещивающимися прямыми?
Расстояние между двумяскрещивающимися прямыми равно
расстоянию от любой точки одной из
этих прямых до плоскости,
проходящей через вторую прямую,
параллельно первой.
Расстояние между двумя
скрещивающимися прямыми равно
расстоянию между двумя
параллельными плоскостями,
содержащими эти прямые.
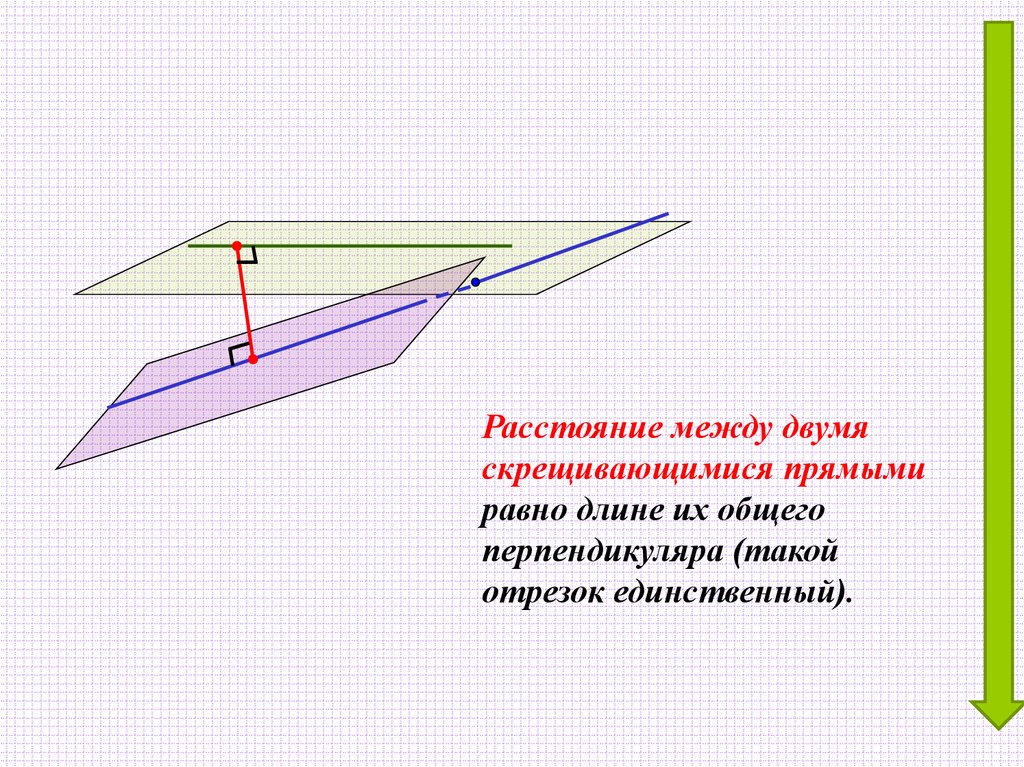
10.
Расстояние между двумяскрещивающимися прямыми
равно длине их общего
перпендикуляра (такой
отрезок единственный).
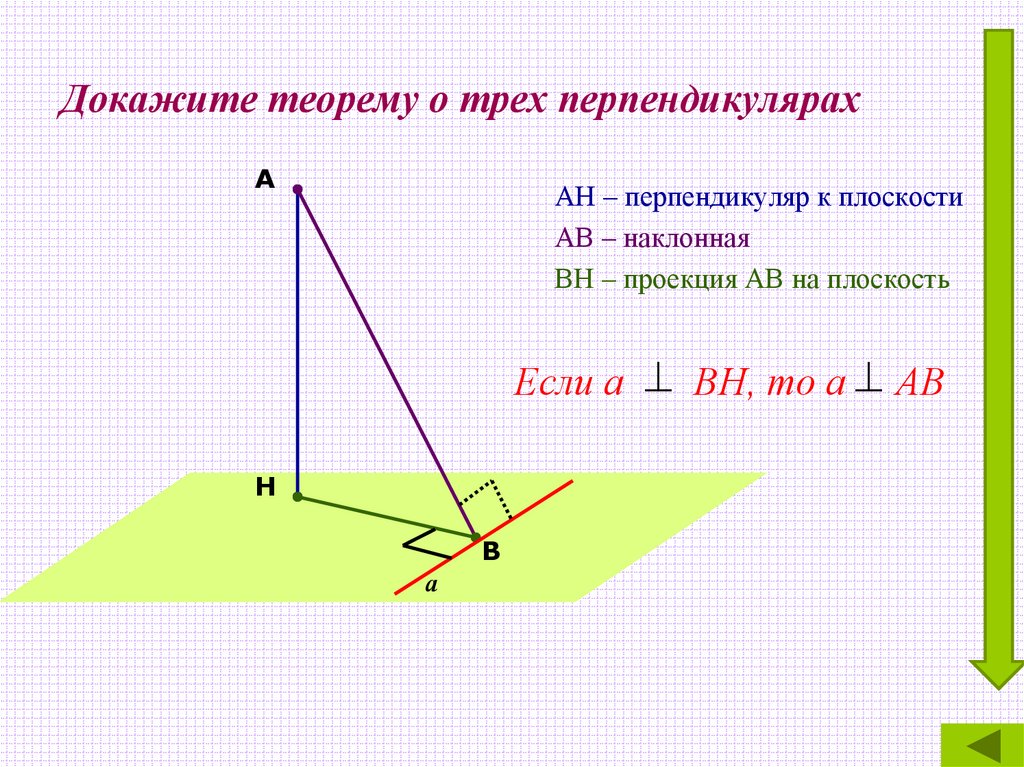
11. Докажите теорему о трех перпендикулярах
ААН – перпендикуляр к плоскости
АВ – наклонная
ВН – проекция АВ на плоскость
Если а ВН, то а АВ
Н
В
а
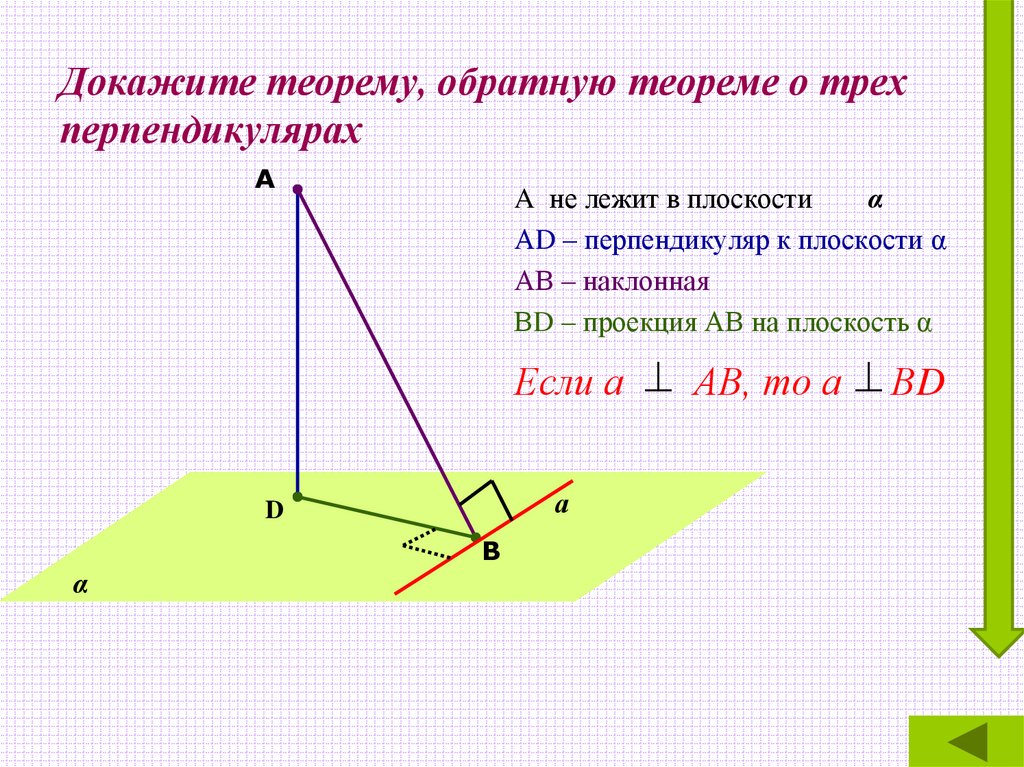
12. Докажите теорему, обратную теореме о трех перпендикулярах
АA не лежит в плоскости
α
АD – перпендикуляр к плоскости α
АВ – наклонная
ВD – проекция АВ на плоскость α
Если а АВ, то а ВD
а
D
В
α
13.
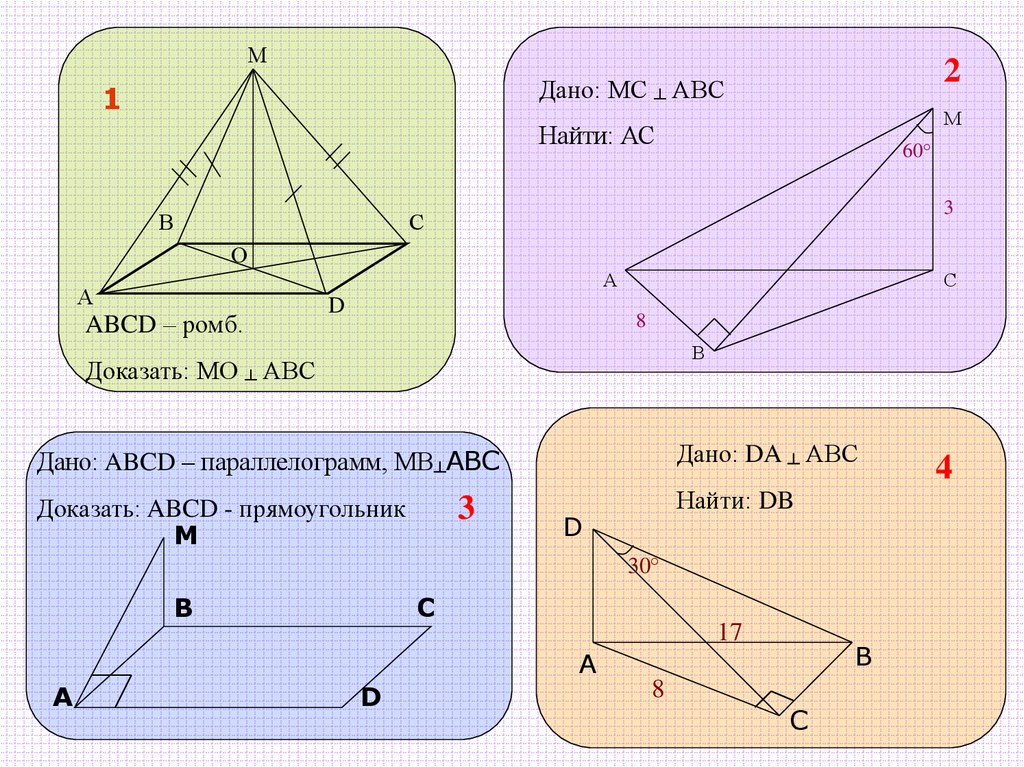
М2
Дано: МС ┴ АВС
1
М
Найти: АС
В
60°
3
С
О
А
А
ABCD – ромб.
D
С
8
В
Доказать: МО ┴ АВС
Дано: ABCD – параллелограмм, МВ┴АВС
Дано: DA ┴ АВС
Доказать: ABCD - прямоугольник
М
Найти: DB
3
D
30°
В
С
17
В
А
А
D
8
С
4
14.
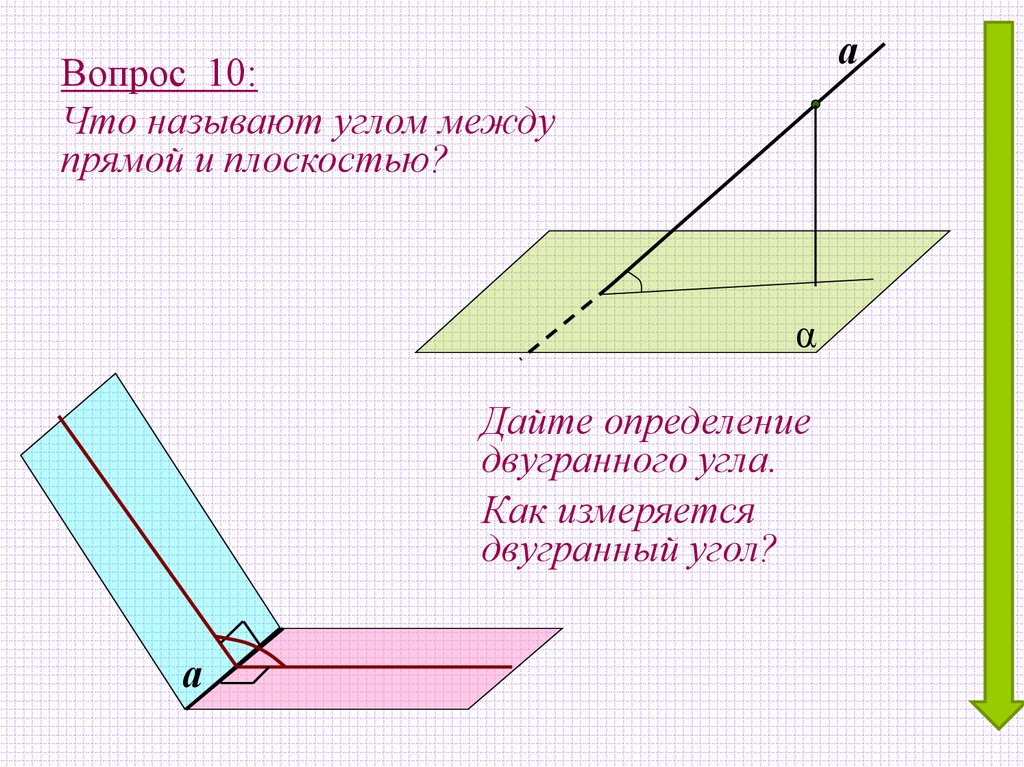
аВопрос 10:
Что называют углом между
прямой и плоскостью?
α
Дайте определение
двугранного угла.
Как измеряется
двугранный угол?
а
15.
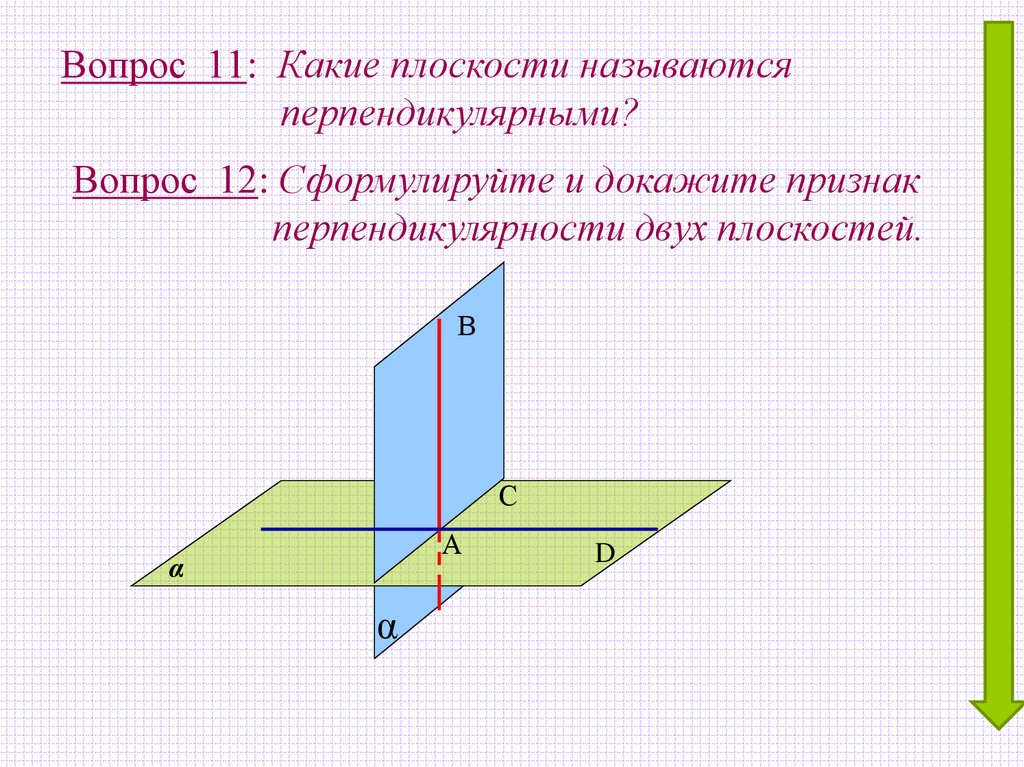
Вопрос 11: Какие плоскости называютсяперпендикулярными?
Вопрос 12: Сформулируйте и докажите признак
перпендикулярности двух плоскостей.
В
С
А
α
α
D
16.
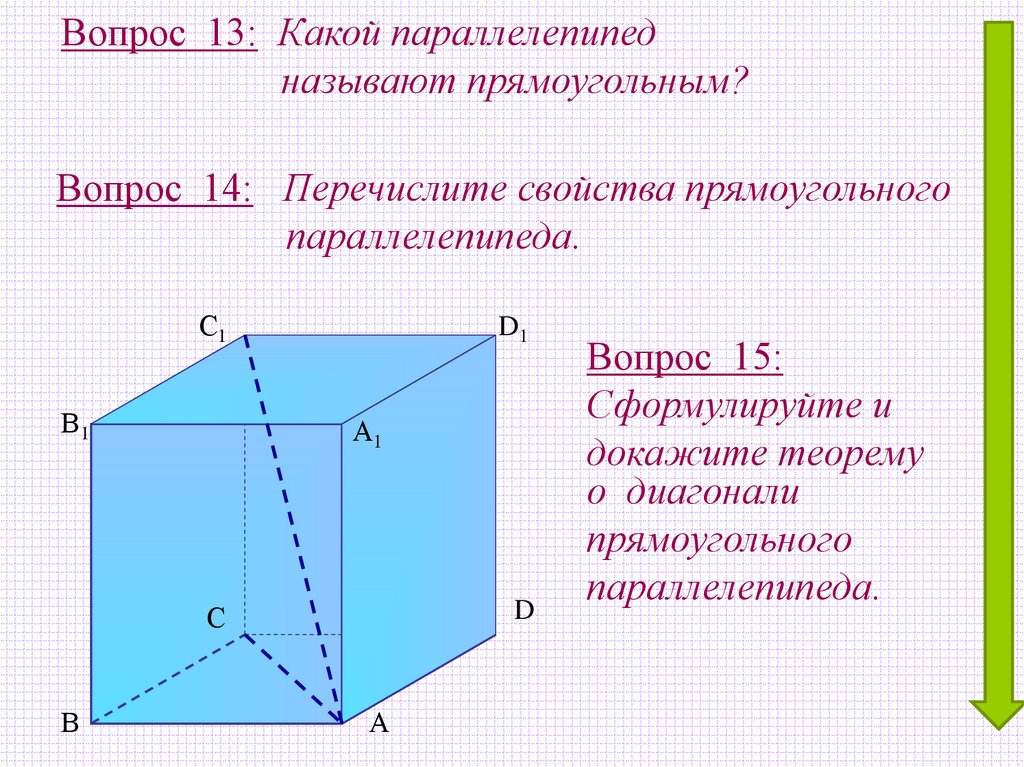
Вопрос 13: Какой параллелепипедназывают прямоугольным?
Вопрос 14: Перечислите свойства прямоугольного
параллелепипеда.
С1
В1
D1
А1
D
С
В
А
Вопрос 15:
Сформулируйте и
докажите теорему
о диагонали
прямоугольного
параллелепипеда.
17.
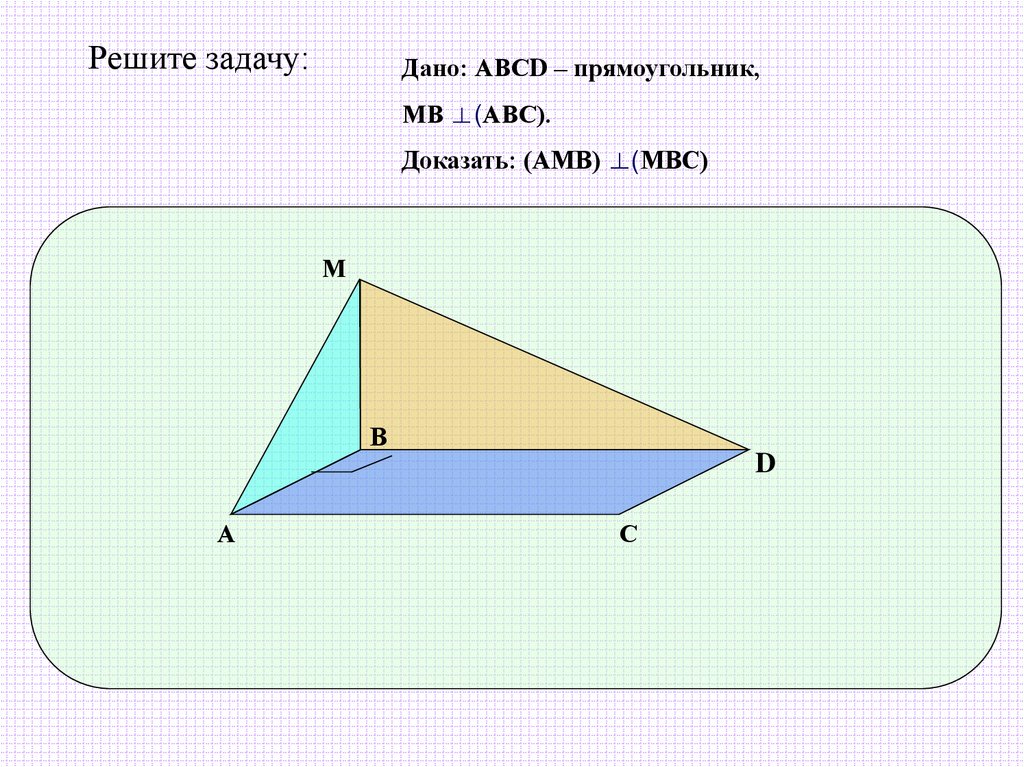
Решите задачу:Дано: АВСD – прямоугольник,
МВ ⊥(АВС).
Доказать: (АМВ) ⊥(МВС)
М
В
D
А
С
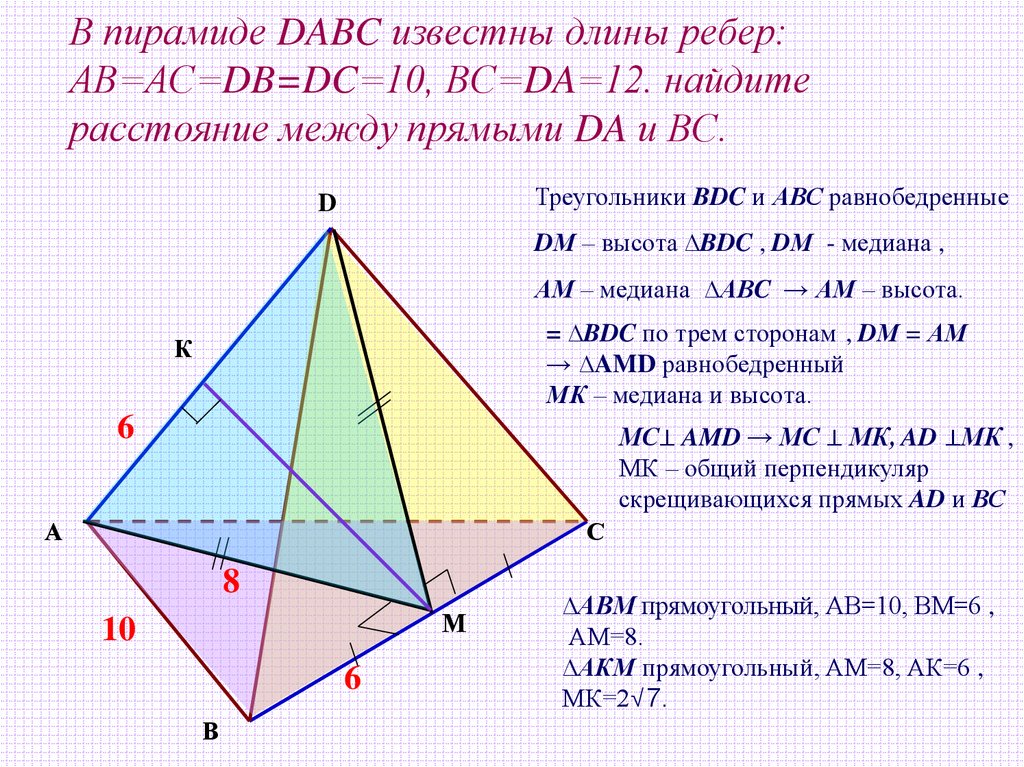
18. В пирамиде DABC известны длины ребер: АВ=АС=DB=DC=10, ВС=DA=12. найдите расстояние между прямыми DA и ВС.
Треугольники BDC и АВС равнобедренныеD
DМ – высота ∆BDC , DМ - медиана ,
АМ – медиана ∆АВC → АМ – высота.
= ∆BDC по трем сторонам , DМ = АМ
→ ∆AMD равнобедренный
МК – медиана и высота.
К
6
МС⊥ AMD → МС ⊥ МК, AD ⊥МК ,
МК – общий перпендикуляр
скрещивающихся прямых AD и ВС
А
С
8
М
10
6
В
∆АВМ прямоугольный, АВ=10, ВМ=6 ,
АМ=8.
∆АКМ прямоугольный, АМ=8, АК=6 ,
МК=2√7.
19.
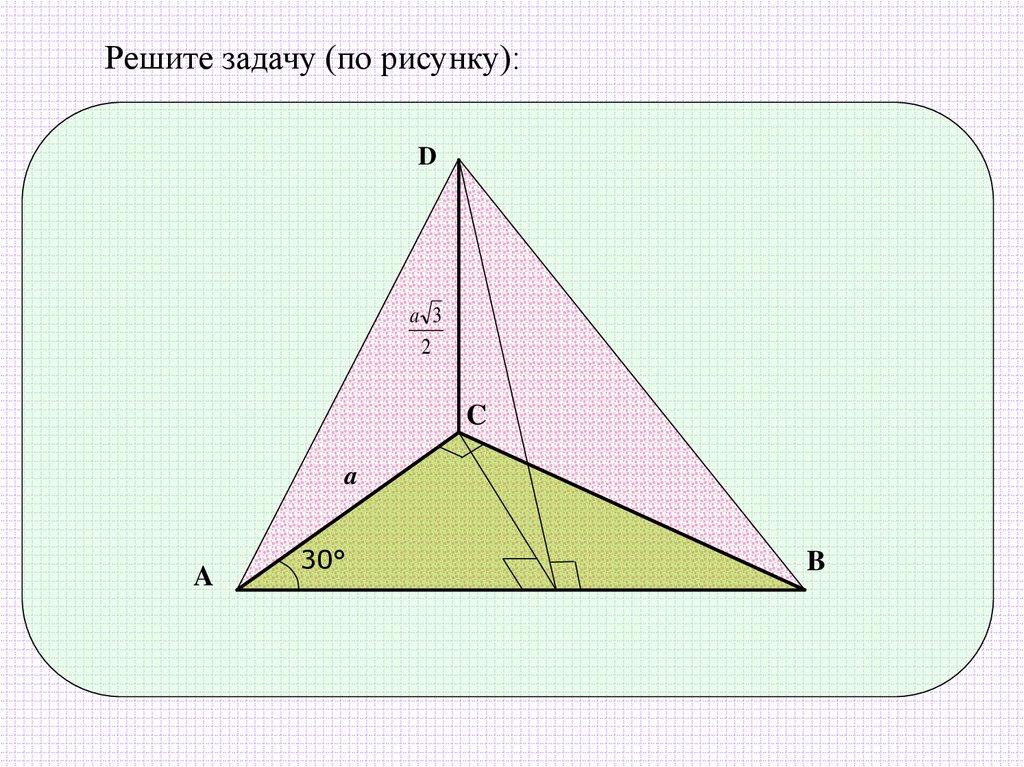
Решите задачу (по рисунку):D
a 3
2
C
a
A
30°
B
20.
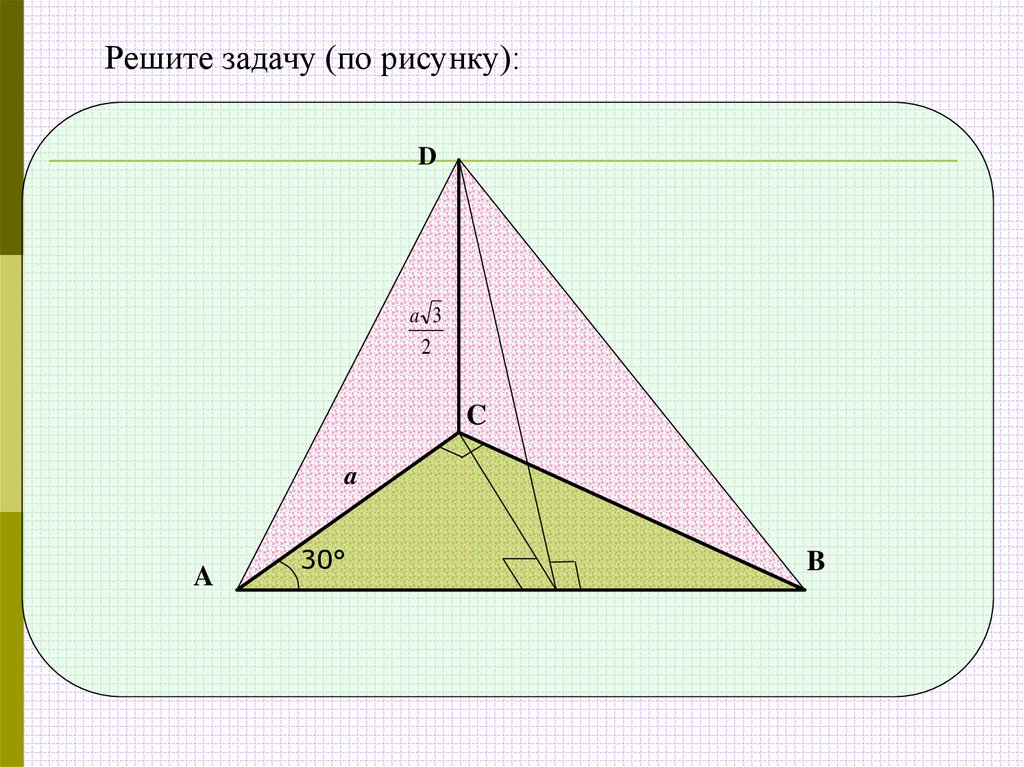
Решите задачу (по рисунку):D
a 3
2
C
a
A
30°
B
21.
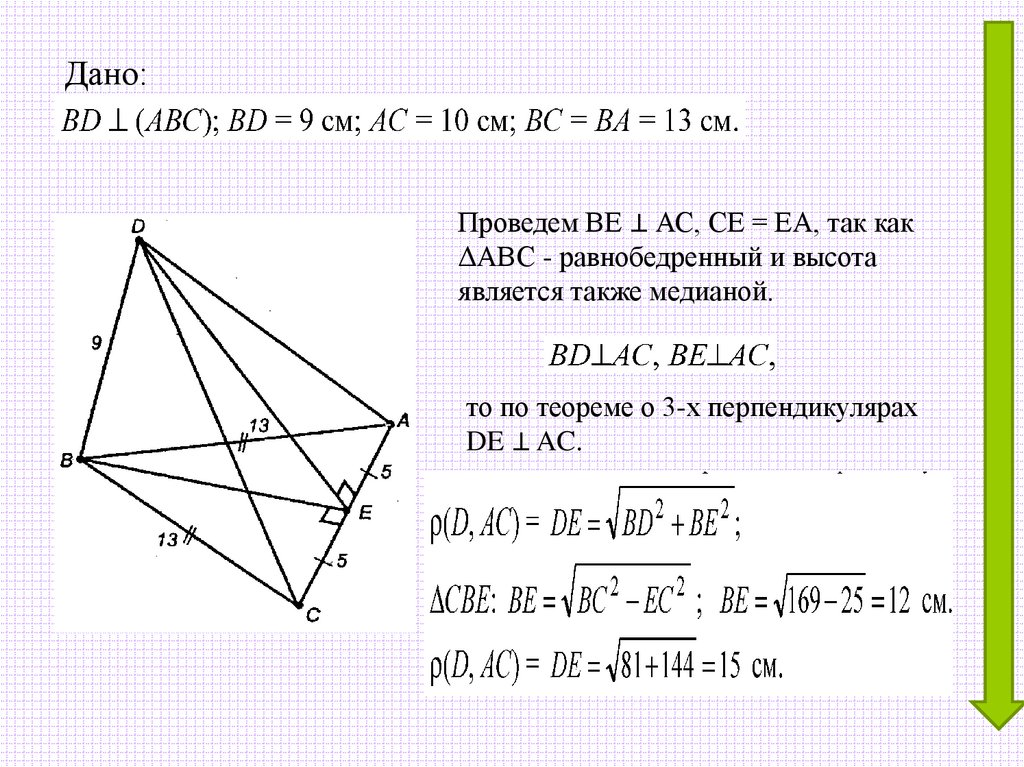
Дано:Проведем ВЕ ⊥ АС, СЕ = ЕА, так как
ΔАВС - равнобедренный и высота
является также медианой.
то по теореме о 3-х перпендикулярах
DE ⊥ AC.
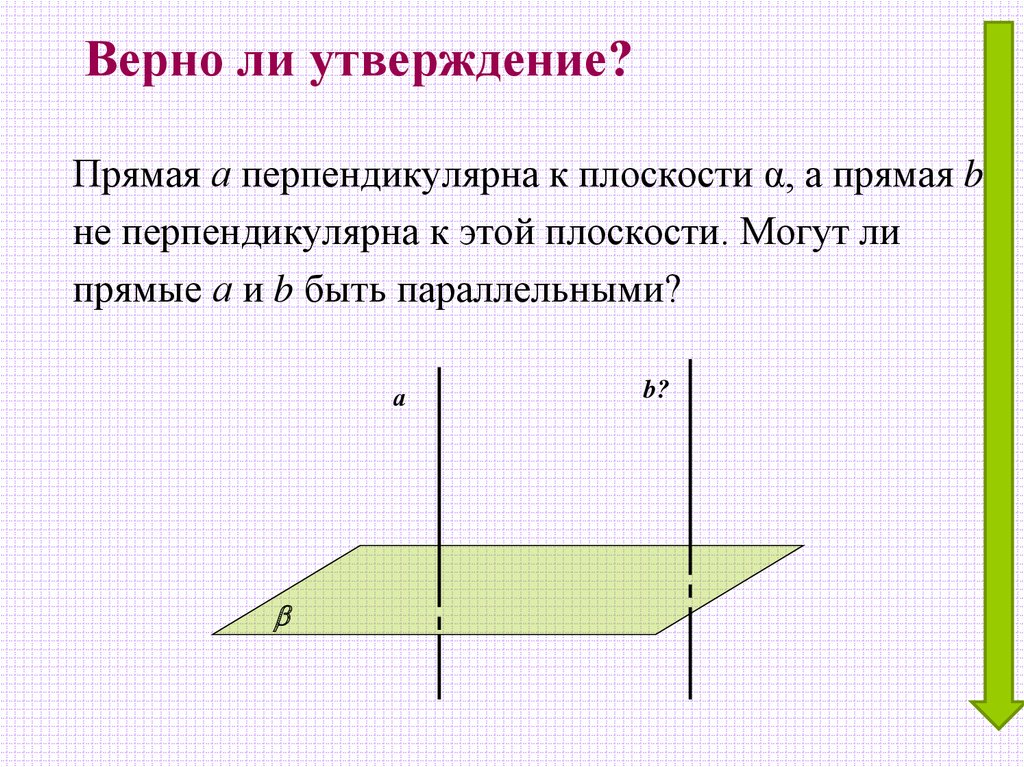
22. Верно ли утверждение?
Прямая а перпендикулярна к плоскости α, а прямая bне перпендикулярна к этой плоскости. Могут ли
прямые а и b быть параллельными?
а
b?
23. Верно ли утверждение?
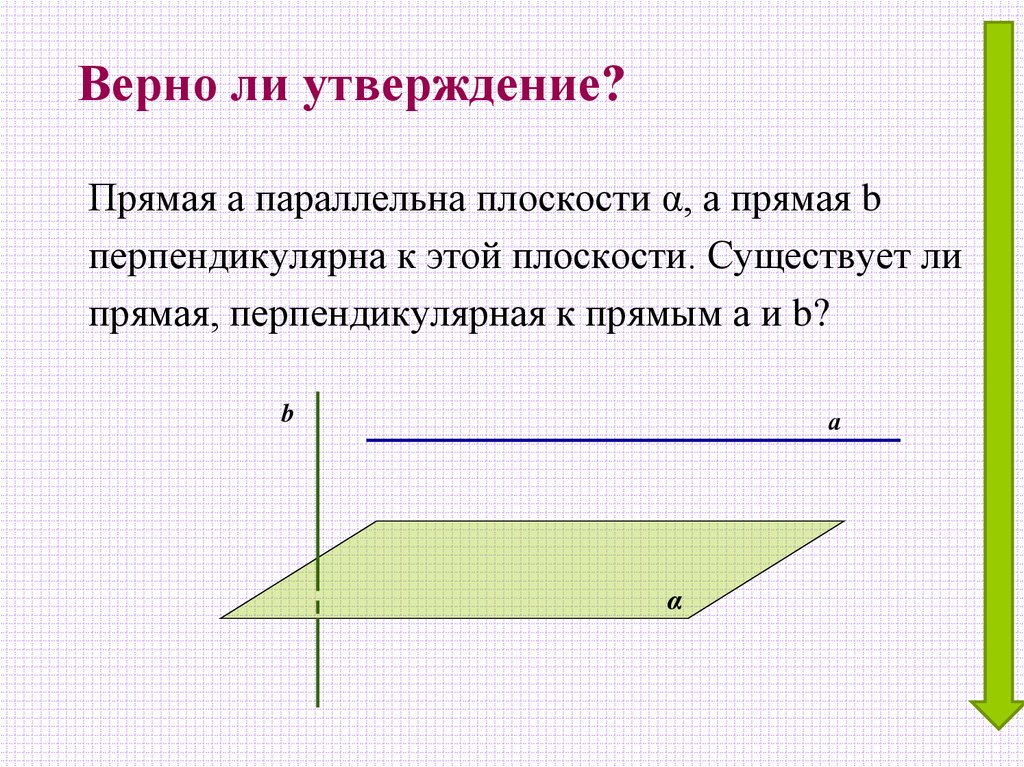
Прямая а параллельна плоскости α, а прямая bперпендикулярна к этой плоскости. Существует ли
прямая, перпендикулярная к прямым а и b?
b
а
α
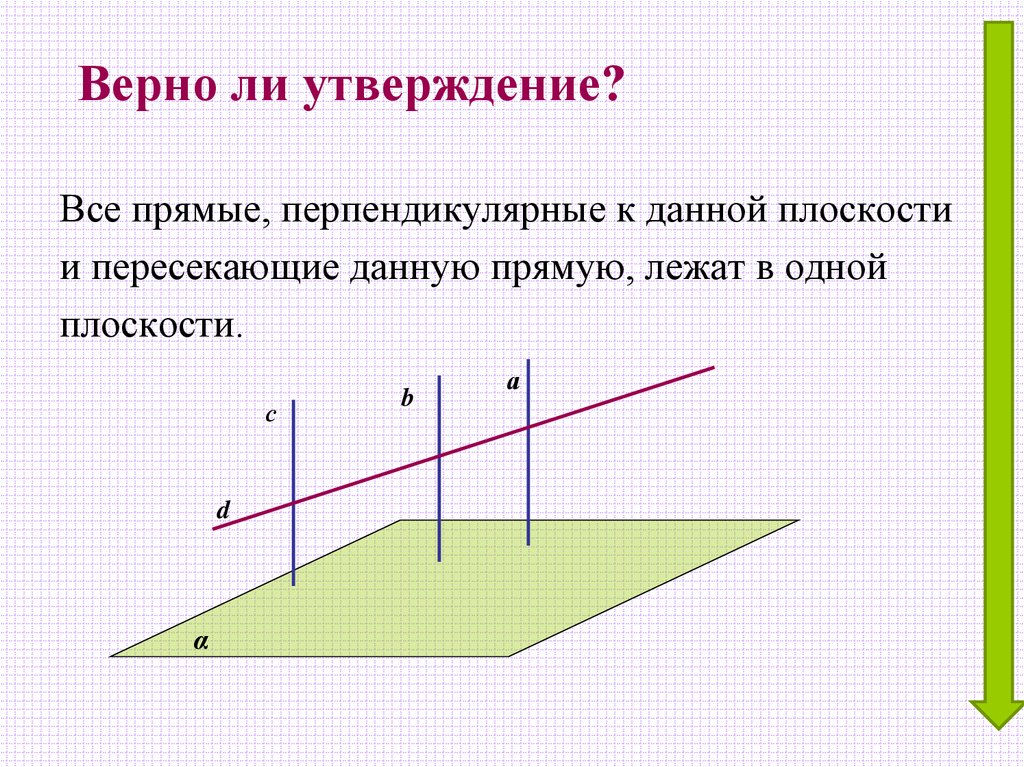
24. Верно ли утверждение?
Все прямые, перпендикулярные к данной плоскостии пересекающие данную прямую, лежат в одной
плоскости.
с
d
α
b
а
25. Верно ли утверждение?
Можно ли через точку пространства провести триплоскости, каждые две из которых взаимно
перпендикулярны?
26.
ИСТОЧНИКИ:Учебник Геометрии 10 класс
АтанасянЛ.С. и др. М.:
Просвещение.
2001
http://5terka.com/node/7155




 mathematics
mathematics








