Перпендикулярность прямых и плоскостей

1. Перпендикулярность прямых и плоскостей.

Перпендикуляр
и
наклонная
ГОУ СПО ВАКЗО
Орлов А.В.

2.

Ит ак, прист упим к делу!
ВВЕСТИ ПОНЯТИЕ
РАССТОЯНИЕОТ ТОЧКИ ДО ПРЯМОЙ
РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
РАССТОЯНИЕ МЕЖДУ ПРЯМОЙ И ПАРАЛЛЕЛЬНОЙ ЕЙ
ПЛОСКОСТЬЮ
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
ДОКАЗАТЬ ТЕОРЕМУ О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
НАУЧИТСЯ ПРИМЕНЯТЬ ТЕОРЕМУ О ТРЕХ
ПЕРПЕНДИКУЛЯРАХ ПРИ РЕШЕНИИ ЗАДАЧ

3.

А
ПОВТОРИТЕ!
С
В
1. Назовите гипотенузу прямоугольного треугольника АВС.
2. Сравните катет и гипотенузу прямоугольного треугольника.
Что больше и почему?
3.
Сформулируйте теорему Пифагора.
4.
Какие прямые называются перпендикулярными?
5. Верно ли утверждение: «прямая перпендикулярна плоскости,
если она перпендикулярна некоторой прямой, лежащей в
этой плоскости».
6. Продолжи предложение: «Прямая перпендикулярна
плоскости, если она . . . »

4.

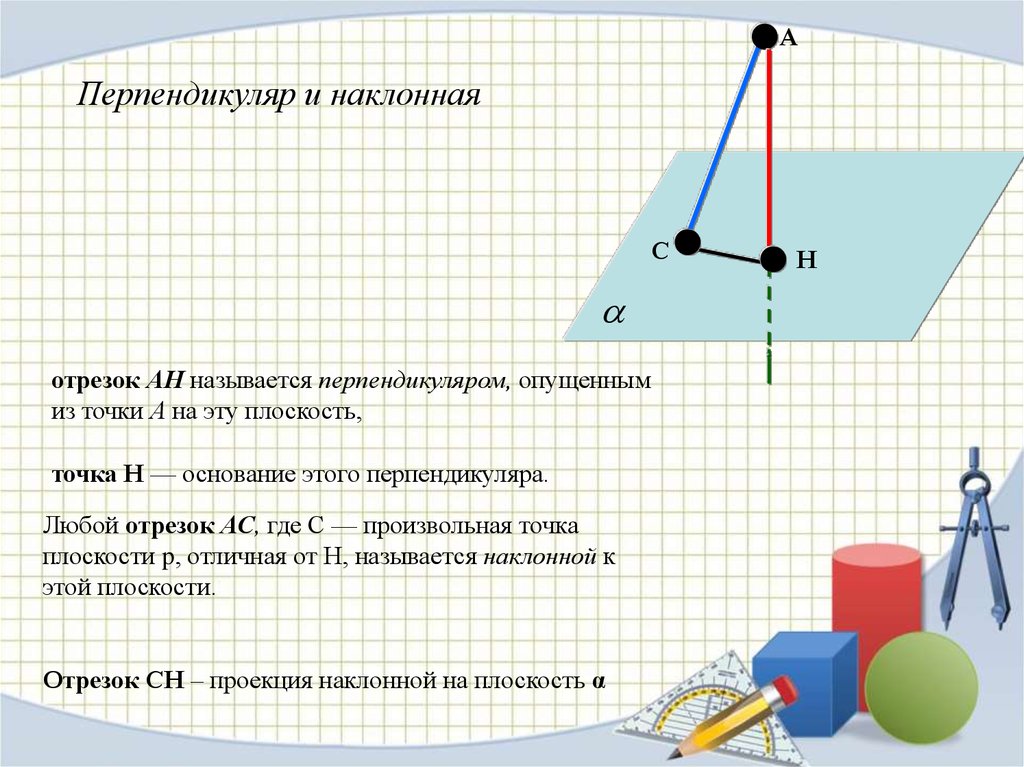
А
Перпендикуляр и наклонная
С
отрезок АН называется перпендикуляром, опущенным
из точки А на эту плоскость,
точка Н — основание этого перпендикуляра.
Любой отрезок АС, где С — произвольная точка
плоскости p, отличная от Н, называется наклонной к
этой плоскости.
Отрезок СН – проекция наклонной на плоскость α
Н

5.

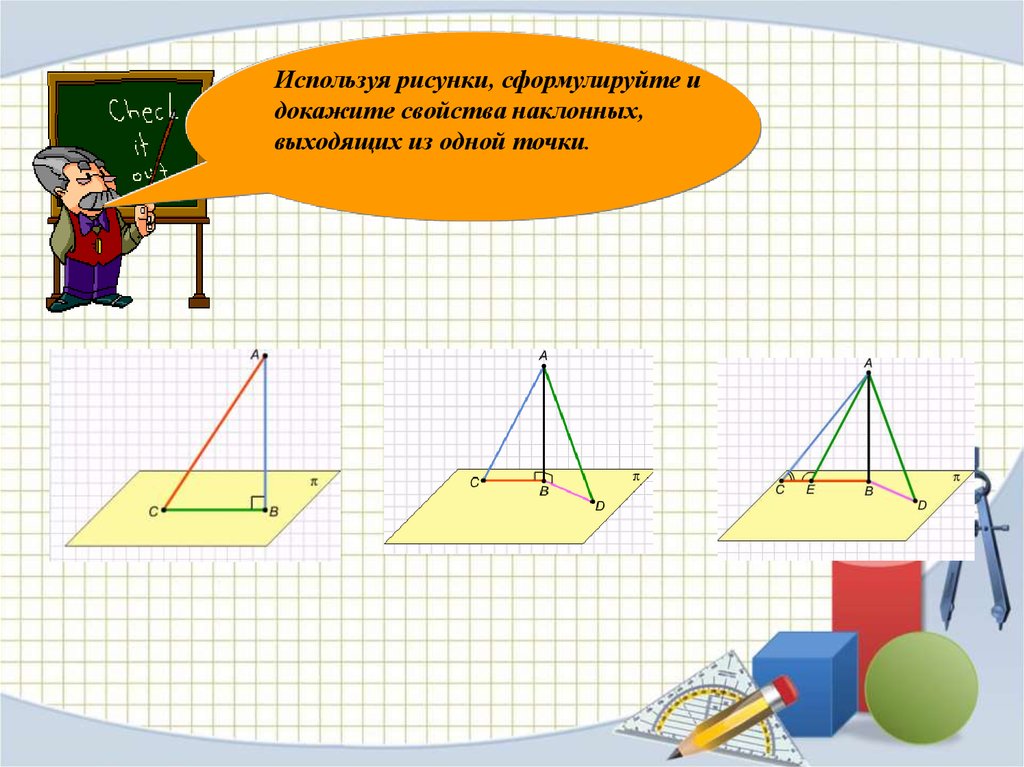
Используя рисунки, сформулируйте и
докажите свойства наклонных,
выходящих из одной точки.

6.

Свойства наклонных, выходящих из одной
точки
1. Перпендикуляр всегда короче наклонной, если они
проведены из одной точки.
2. Если наклонные равны, то равны и их
проекции, и наоборот.
3. Большей наклонной соответствует
большая проекция и наоборот.

7.

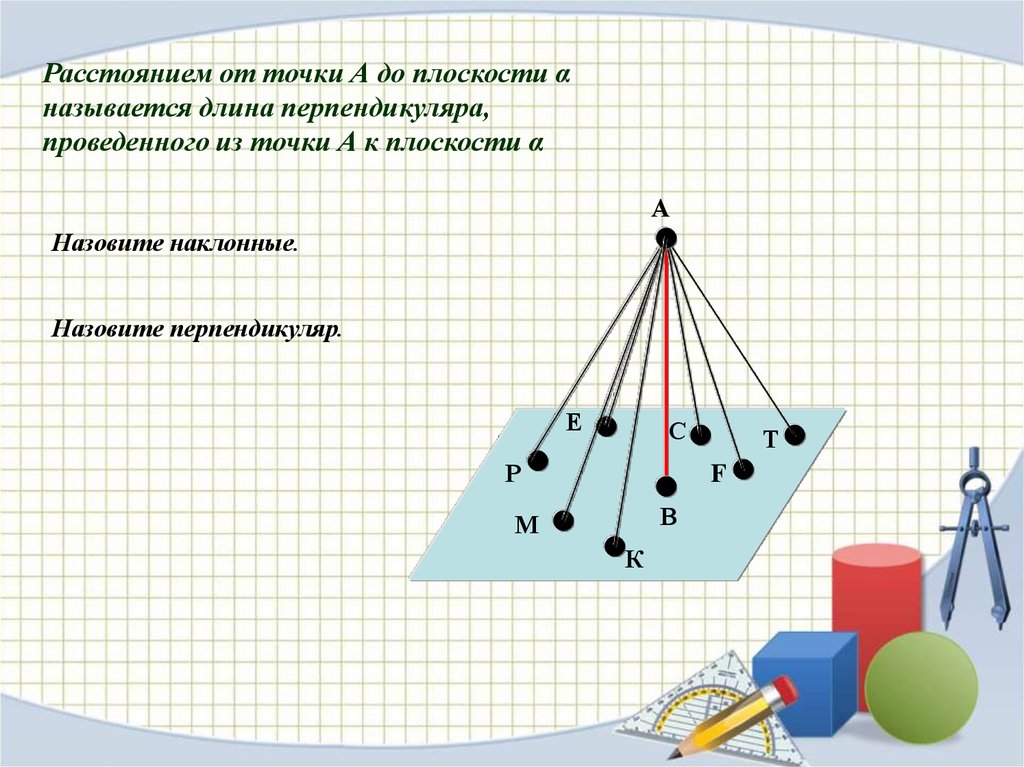
Расстоянием от точки А до плоскости α
называется длина перпендикуляра,
проведенного из точки А к плоскости α
А
Назовите наклонные.
Назовите перпендикуляр.
Е
С
Р
Т
F
В
М
К

8.

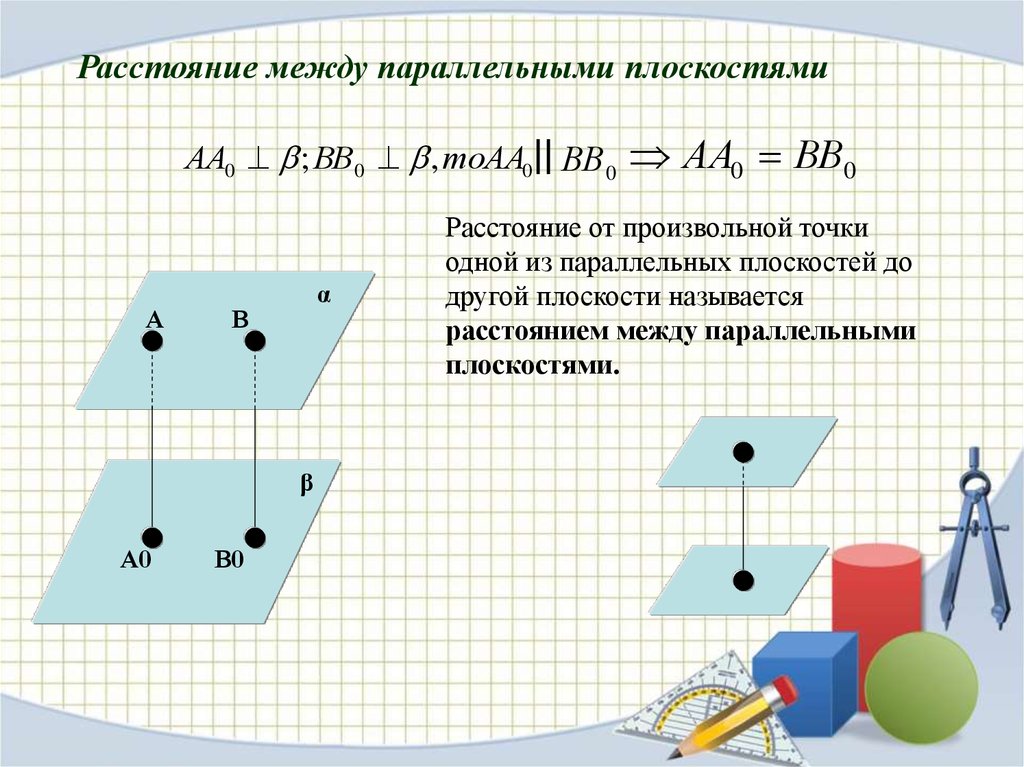
Расстояние между параллельными плоскостями
АА0 ; ВВ0 , тоАА0 || ВВ 0
А
α
В
β
А0
В0
АА0 ВВ0
Расстояние от произвольной точки
одной из параллельных плоскостей до
другой плоскости называется
расстоянием между параллельными
плоскостями.

9.

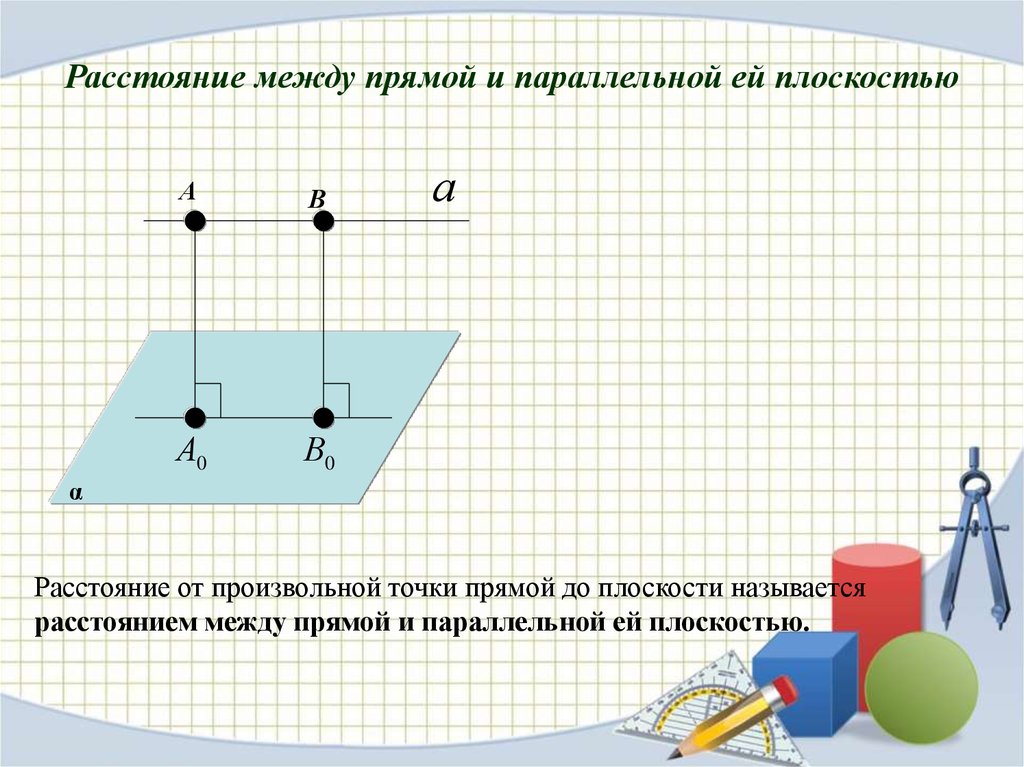
Расстояние между прямой и параллельной ей плоскостью
А
В
А0
В0
а
α
Расстояние от произвольной точки прямой до плоскости называется
расстоянием между прямой и параллельной ей плоскостью.

10.

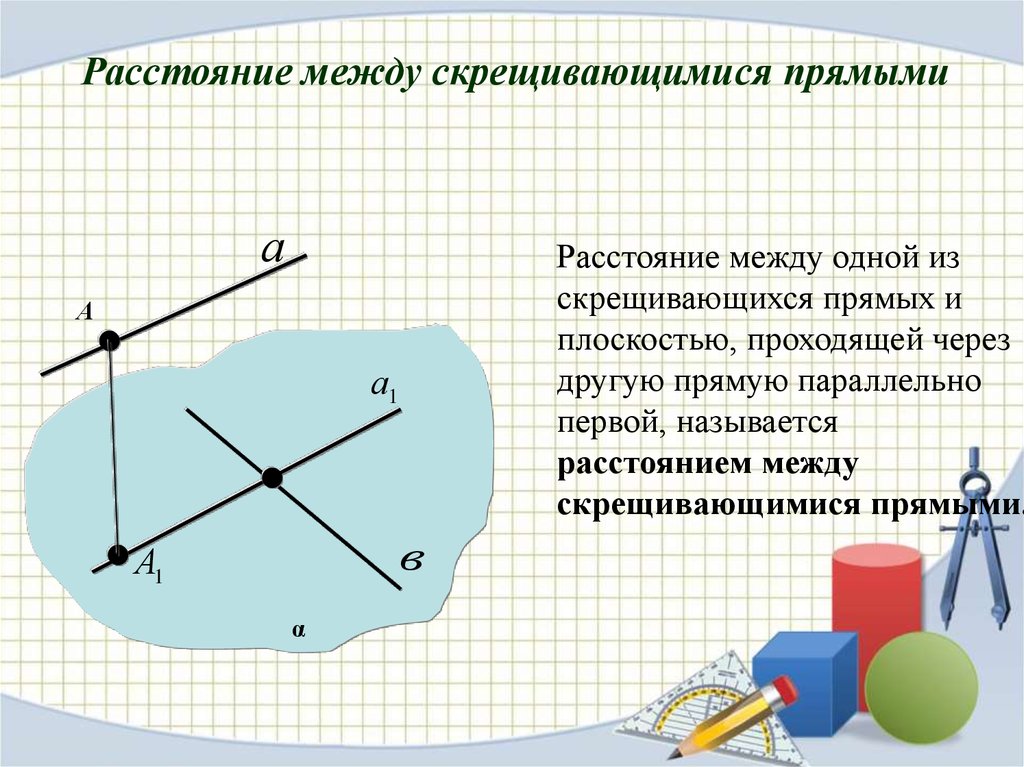
Расстояние между скрещивающимися прямыми
а
Расстояние между одной из
скрещивающихся прямых и
плоскостью, проходящей через
другую прямую параллельно
первой, называется
расстоянием между
скрещивающимися прямыми.
А
а1
в
А1
α

11.

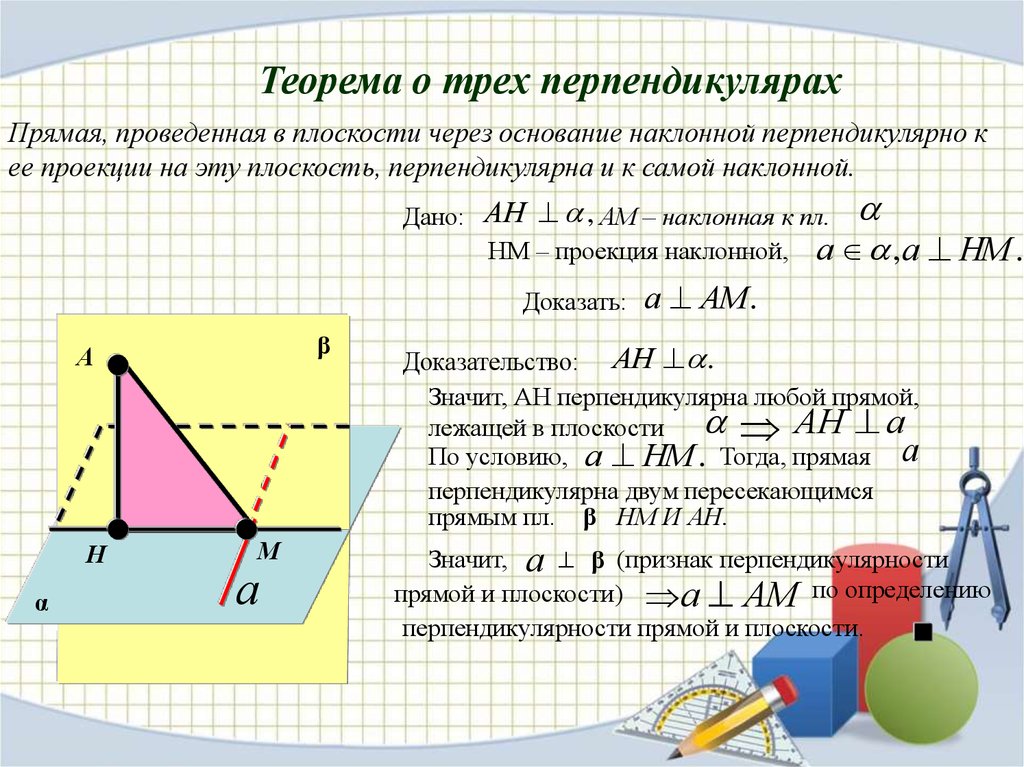
Теорема о трех перпендикулярах
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к
ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Дано: АН , АМ – наклонная к пл.
НМ – проекция наклонной, а , а
Доказать:
β
А
Н
α
М
а
НМ .
а АМ.
Доказательство: АН .
Значит, АН перпендикулярна любой прямой,
АН а
лежащей в плоскости
По условию, а НМ . Тогда, прямая а
перпендикулярна двум пересекающимся
прямым пл. β НМ И АН.
Значит, а β (признак перпендикулярности
прямой и плоскости) а АМ по определению
перпендикулярности прямой и плоскости.

12.

Теорема обратная теореме о трех
перпендикулярах
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней , перпендикулярна и к её
проекции.
Задача 153, стр.45, дома разобрать самостоятельно.

13.

А т еперь задача

14.

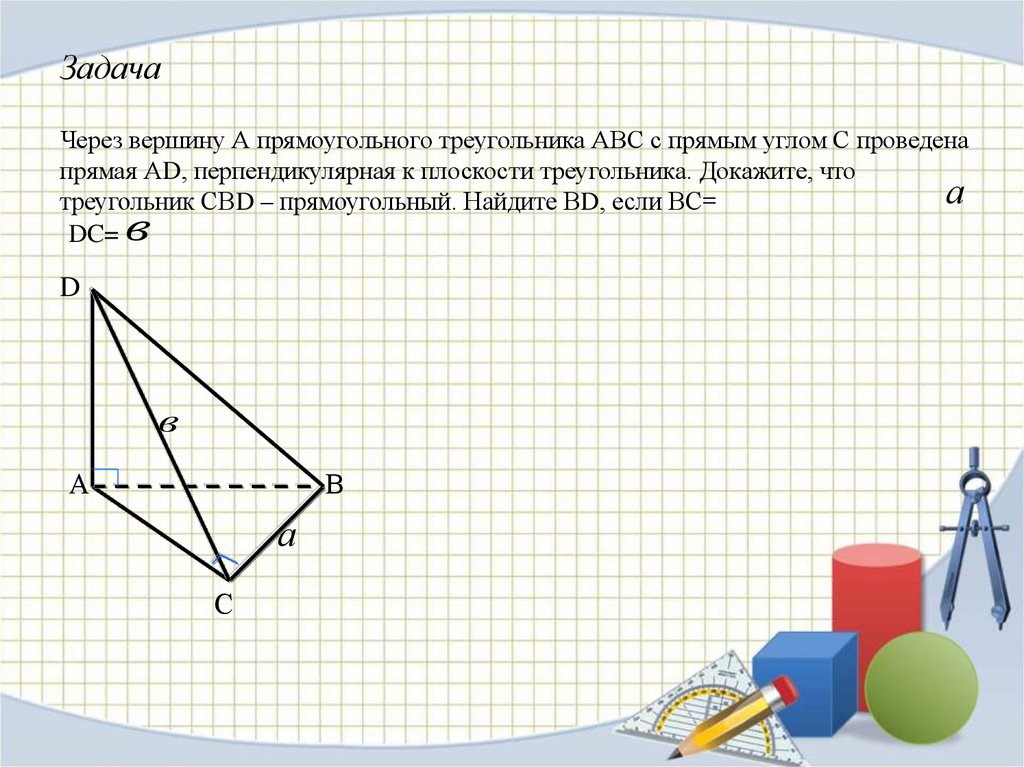
Задача
Через вершину А прямоугольного треугольника АВС с прямым углом С проведена
прямая АD, перпендикулярная к плоскости треугольника. Докажите, что
а
треугольник СВD – прямоугольный. Найдите ВD, если ВС=
DC=
в
D
в
А
В
а
С

15.

Урок окончен.
Всем спасибо.
Домашнее задание:

16.

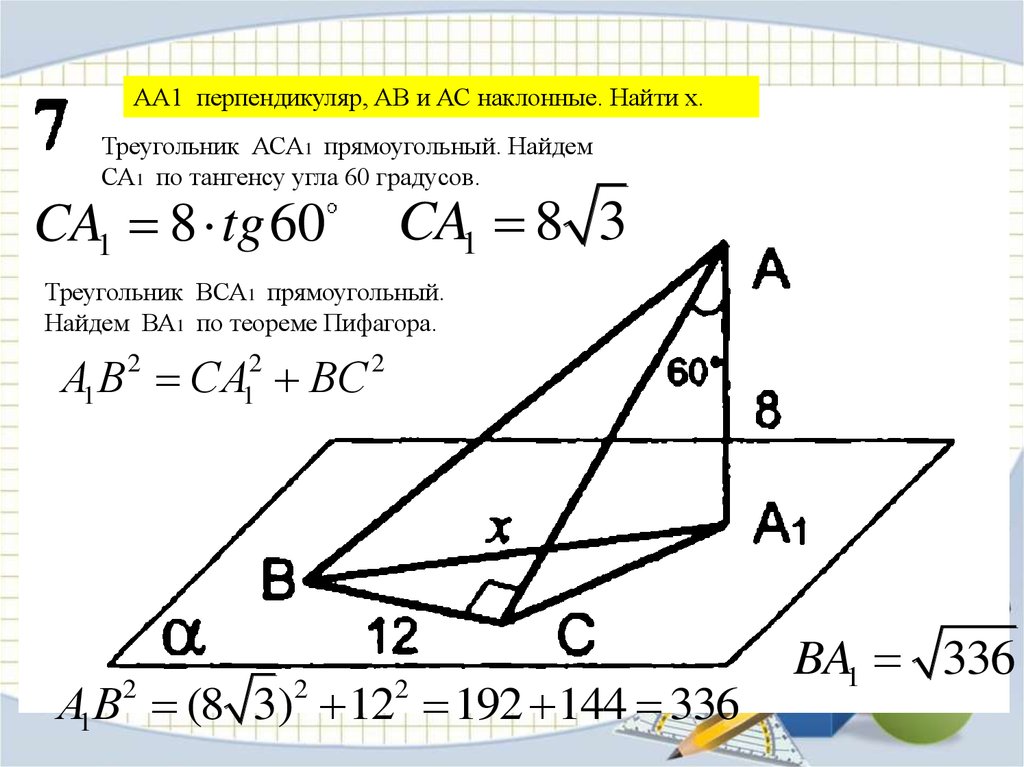
АА1 перпендикуляр, АВ и АС наклонные. Найти х.
Треугольник АСА1 прямоугольный. Найдем
СА1 по тангенсу угла 60 градусов.
CA1 8 tg 60
CA1 8 3
Треугольник ВСА1 прямоугольный.
Найдем ВА1 по теореме Пифагора.
А1 B 2 CА12 BC 2
А1B (8 3) 12 192 144 336
2
2
2
BA1 336

17.

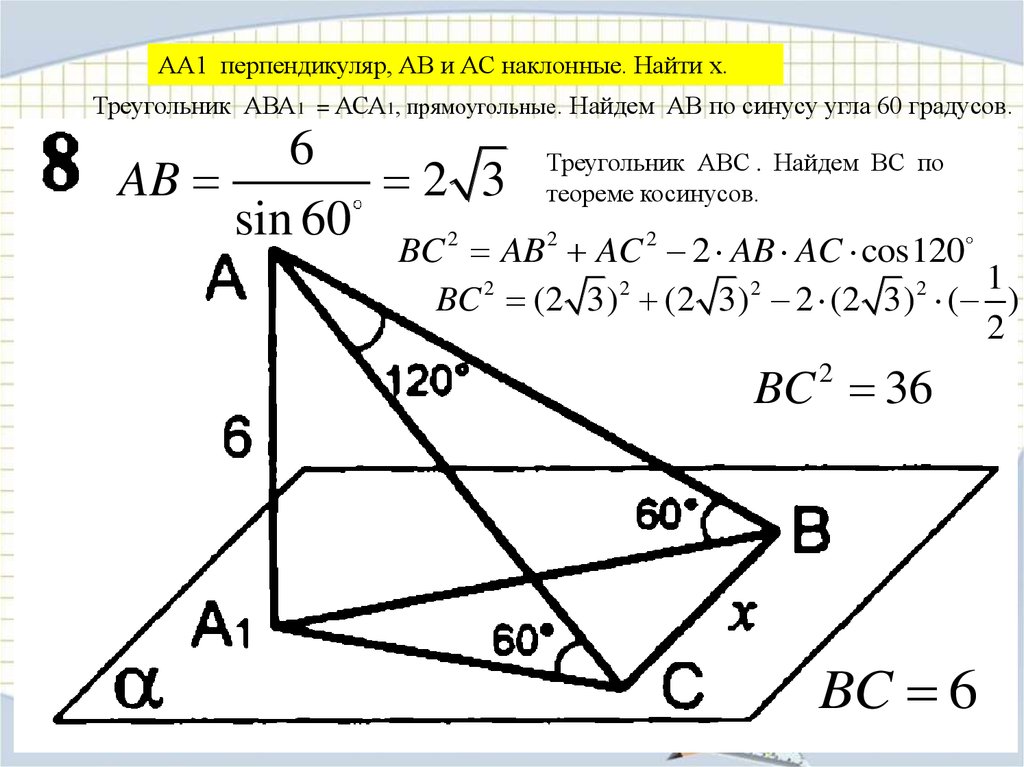
АА1 перпендикуляр, АВ и АС наклонные. Найти х.
Треугольник АВА1 = АСА1, прямоугольные. Найдем АВ по синусу угла 60 градусов.
6
AB
2 3
sin 60
2
Треугольник АВС . Найдем ВС по
теореме косинусов.
BC AB 2 AC 2 2 AB AC cos120
1
2
2
2
2
BC (2 3) (2 3) 2 (2 3) ( )
2
BC 2 36
BC 6

18.

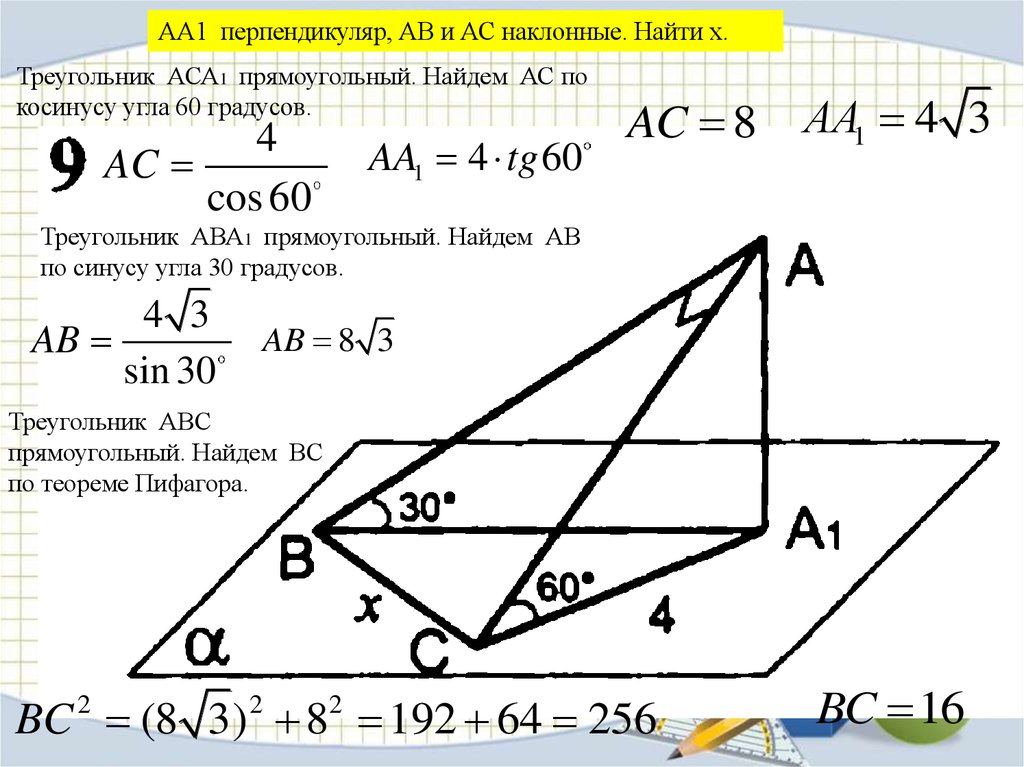
АА1 перпендикуляр, АВ и АС наклонные. Найти х.
Треугольник АСА1 прямоугольный. Найдем АС по
косинусу угла 60 градусов.
4
AC
cos 60
AA1 4 tg 60
AC 8
АА1 4 3
Треугольник АВА1 прямоугольный. Найдем АВ
по синусу угла 30 градусов.
4 3
AB
sin 30
AB 8 3
Треугольник АВС
прямоугольный. Найдем ВС
по теореме Пифагора.
BC 2 (8 3) 2 82 192 64 256
BC 16

19.

Литература
1. Геометрия. Учебник для 10-11 классов общеобразовательной
школы, Атанасян Л.С., Бутузов В.Ф. и др., издательство:
"Просвещение" 2002г