3. Элементы векторной алгебры

1. Элементы векторной алгебры

2. Вектора

3.

Пусть М произвольная точка пространства. Через
точку М проведем три плоскости перпендикулярные
осям координат. Точки пересечения с осями координат
обозначим M x , M y , M z .
Прямоугольными координатами точки М называют
числа x OM x , y OM y , z OM z .

4.

Определение:
отрезок.
Вектором
называется
направленный
Вектор обозначают: a или AB .
Определение: Длиной вектора
между его началом и концом.
называется расстояние
Определение: Векторы называются коллинеарными, если
они лежат на одной прямой или на параллельных прямых.
Коллинеарные векторы могут быть
направлены или противоположно направлены.
одинаково

5.

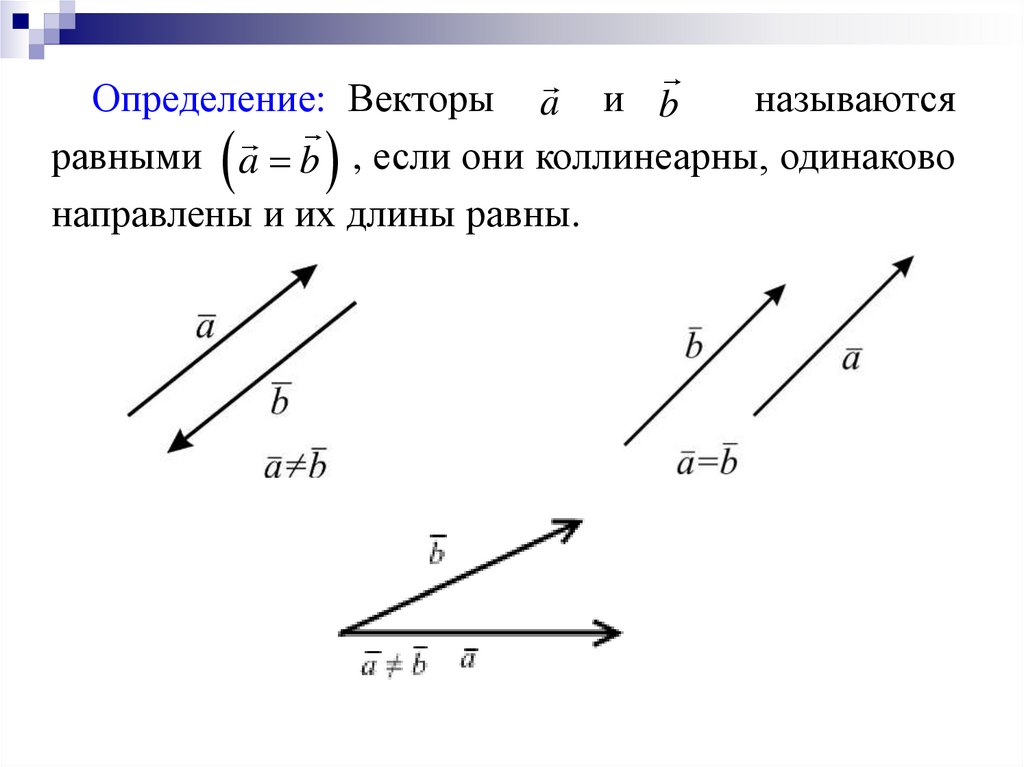
Определение: Векторы a и b
называются
равными a b , если они коллинеарны, одинаково
направлены и их длины равны.

6. Проекция вектора на ось

Пусть в пространстве задана ось u и вектор AB .
Определение: Проекцией вектора AB на ось u
называется длина отрезка A1B1 , заключенного между
проекциями начала и конца вектора на эту ось.

7.

Если направление A1B1 совпадает с направлением
оси u, то A1B1 A1B1 .
Если направление A1B1 противоположно
направлению оси u, то A1B1 A1B1 .
Проекцию вектора AB на ось u обозначают:
npu AB

8.

Теорема: Проекция вектора AB на ось u равна
произведению длины вектора AB на косинус угла
между положительным направлением оси u и
вектором AB:
npu AB AB cos

9. Проекция вектора на оси координат

Теорема: Каковы бы ни были две точки A( x1 ; y1 ; z1 )
и B ( x2 ; y2 ; z2 ) , координаты вектора
AB (ax ; a y ; az )
определяются по формулам:
ax x2 x1 , a y y2 y1 , az z2 z1
Длина вектора
a определяется по формуле:
a ax 2 a y 2 az 2,
где a (ax ; a y ; az ) – координаты вектора a .
Если вектор AB выходит из начала координат, то его
координаты равны координатам конца вектора:
AB ( x2 ; y2 ; z2 )

10. Разложение вектора по базису

Определение: Тройка единичных векторов
осей координат i , j , k , каждый из которых одинаково
направлен с соответствующей осью координат
называется базисом.
Теорема: Любой вектор a единственным образом
может быть разложен по базису i , j , k
, то есть
представлен в виде: a axi a y j az k ,
где ax , a y , az – координаты вектора a .

11. Направляющие косинусы вектора

Пусть дан вектор a (ax ; a y ; az ) , который выходит
из начала координат и не лежит ни в одной из
координатных плоскостей. Через точку А проведем
плоскости перпендикулярные осям.
Вместе с осями координат
они образуют параллелепипед,
диагональю которого является
отрезок ОА.

12.

Направление вектора a определяется углами , , ,
образованными им с осями координат Ох, Оу и Оz.
Косинусы этих углов называются направляющими
косинусами вектора a и определяются по формулам:
ax
cos
a
cos
ay
a
az
cos ,
a
где a ax 2 a y 2 az 2 – длина вектора.
Направляющие
косинусы
вектора
соотношением:
cos 2 cos 2 cos 2 1
связаны

13. Линейные операции над векторами

14.

Определение: Суммой a b называется вектор,
который выходит из начала вектора a и приходит в
конец вектора b , при условии, что вектор b ,
приложен к концу вектора a .

15.

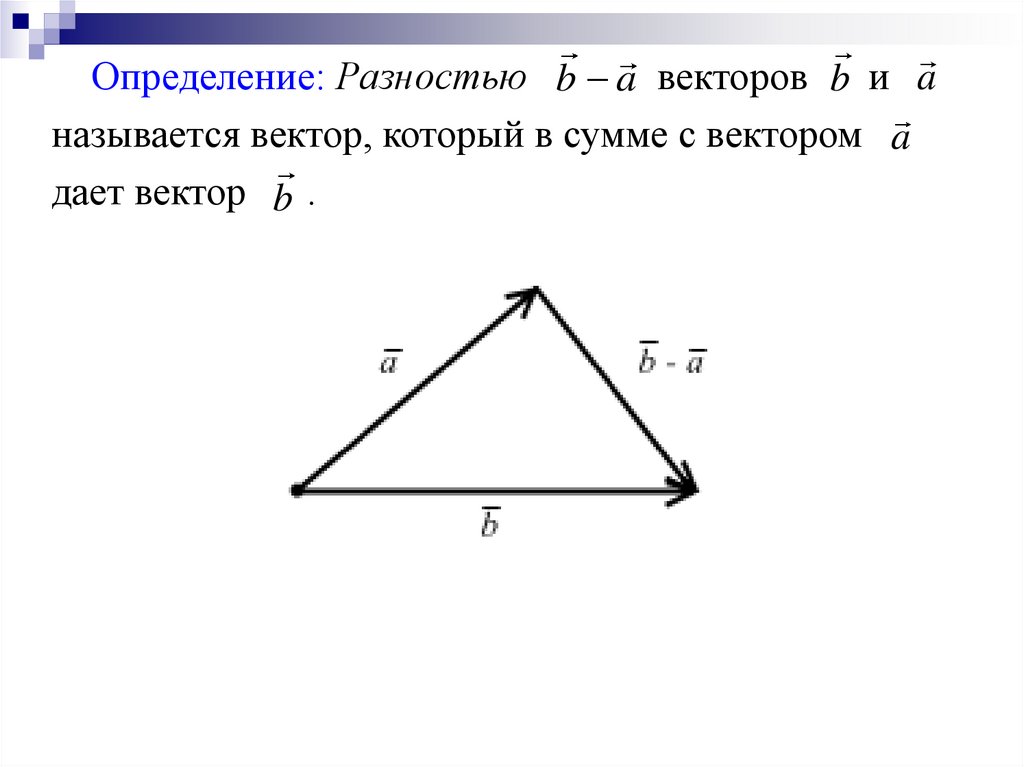
Определение: Разностью b a векторов b и a
называется вектор, который в сумме с вектором a
дает вектор b .

16.

Если векторы a и b заданы их разложением
по базису a axi a y j az k и b bxi by j bz k , то
их сумма и разность определяются по формулам:
a b (ax bx )i (a y by ) j (az bz )k
a b (ax bx )i (a y by ) j (az bz )k

17.

Определение: Произведением вектора a на число
называется вектор a , который коллинеарен вектору a и
имеет длину равную a , и направление совпадающее
с направлением вектора a при 0 , и противоположное,
при 0 .
Если 0 , то a 0 .

18. Скалярное произведение векторов

19.

Определение: Скалярным произведением двух
ненулевых векторов a и b называется число
(скаляр), равное произведению длин этих векторов
на косинус угла между ними:
a b a b cos
(1)

20. Свойства скалярного произведения

1. Скалярное произведение двух векторов равно 0,
если векторы взаимно перпендикулярны, или один из
них является нулевым вектором, то есть
a b 0 , если a b , либо a 0 , либо b 0 .
2. Скалярный квадрат векторов равен квадрату его
2
длины: a a a .
3. Скалярное произведение не изменится, если
вектора поменять местами: a b b a .
4. Скалярное произведение равно произведению
длины одного из векторов на проекцию другого вектора
по направлению первого: a b a npa b b npb a .

21. Выражение скалярного произведения через координаты векторов

Теорема: Если векторы a и b заданы своими
координатами a axi a y j az k и b bxi by j bz k,
тогда скалярное произведение этих векторов
находится по формуле:
a b axbx a yby azbz
(2)

22. Угол между векторами

Воспользуемся скалярным произведением двух
векторов: a b a b cos .
Откуда cos
a b
.
a b
Так как a b axbx a yby azbz , а
a ax a y az
2
cos
2
b bx 2 by 2 bz 2 , то
и
2
axbx a yby az bz
a a a b b b
2
x
2
y
2
z
2
x
2
y
2
z
(3)

23.

Если векторы a и b перпендикулярны, то a b 0,
или
axbx a yby az bz 0
(4)
(4) – условие перпендикулярности двух векторов.
Пример: Определить угол между векторами
a 2i 3 j 6k
и
b 3i 4 j .
Решение:
По формуле (3) имеем:
18 1
cos
3
22 ( 3) 2 62 32 ( 4) 2 35 2
2 3 ( 3)( 4) 6 0

24. Векторное произведение векторов

25.

Определение: Векторы a , b и c называются
компланарными, если они лежат в одной плоскости
или в параллельных плоскостях.
Определение: Упорядоченная тройка (a, b , c )
некомпланарных векторов называется правой, если
после приведения их к общему началу из конца
третьего вектора кратчайший поворот от первого ко
второму совершается против хода часовой стрелки.
В противном случае тройка векторов называется
левой.

26.

Определение: Векторным произведением двух
ненулевых векторов a и b называется вектор c ,
удовлетворяющий условиям:
1. c a b sin ;
(5)
2. c a , c b ;
3. векторы a , b , c образуют правую тройку
векторов.

27. Свойства векторного произведения

1. Векторное произведение двух векторов равно 0,
если векторы коллинеарны, или один из них является
нулевым вектором, то есть a b 0 , если a b , либо
a 0 , либо b 0 .
2. Векторное произведение изменит знак, если
векторы поменять местами: a b b a.
3. Длина векторного произведения двух
неколлинеаных векторов a и b равна площади
параллелограмма, построенного на этих векторах:
S a b

28. Выражение векторного произведения через координаты векторов

Теорема: Если векторы a и b заданы своими
координатами a axi a y j az k и b bxi by j bz k,
тогда векторное произведение этих векторов
находится по формуле:
i
a b ax
bx
j
ay
by
k
ay
az i
by
bz
az
ax
j
bz
bx
ax
az
k
bx
bz
ay
by (6)

29.

Пример: Найти площадь треугольника с вершинами
A(2; 1; 3) , B(1; 3; 5) , C (0; 2; 3) .
Решение:
Найдем векторы a CA и b CB .
a (2 0)i ( 1 2) j (3 3)k 2i j 6k
b (1 0)i (3 2) j ( 5 3)k i 5 j 2k
i
j
k
a b 2 1 6 32i 10 j 9k
1 5 2
1
1
1
2
2
2
S a b
( 32) 10 9
1205 кв. ед.
2
2
2

30. Смешанное произведение векторов

31.

Определение: Смешанным произведением трех
ненулевых векторов a , b и c называется число,
равное скалярному произведению вектора a на
векторное произведение векторов b и c , то есть
a (b c )

32. Выражение смешанного произведения через координаты векторов

Теорема: Если векторы a , b и c заданы своими
координатами a axi a y j az k , b bxi by j bz k и
c cxi c y j cz k , тогда смешанное произведение
этих векторов находится по формуле:
ax
a b c bx
cx
ay
by
cy
az
bz
cz
(7)

33.

Необходимым
и
достаточным
компланарности трех векторов является:
ax
bx
cx
ay
by
cy
az
bz 0
cz
условием
(8)

34.

Теорема: Смешанное произведение a (b c ) трех
векторов a , b и c по модулю равно объему
параллелепипеда, построенного на этих векторах:
V a b c
Объем треугольной пирамиды (тетраэдра),
образованной этими векторами определяется по
формуле:
1
Vпир a b c
(9)
6

35.

Пример: Найти объем пирамиды с вершинами:
A(1; 2; 3) , B(0; 1;1) , C (2; 5; 2) , D(3; 0; 2) .
Решение:
Найдем векторы a AB, b AC и c AD .
a i 3 j 2k , b i 3 j k , c 2i 2 j 5k .
По формуле (9) имеем:
1 3 2
1
1
Vпир a b c 1 3 1
6
6
2 2 5
1 1
1 3
1 3 1
1
3
2
24 4 куб. ед.
2 5
2 2 6
6 2 5