геометрия 8 класс 29 урок

1.

ОПРЕДЕЛЕНИЕ
ПОДОБНЫХ
ТРЕУГОЛЬНИКОВ.
п. 63, 64

2.

ПОВТОРИМ!
Что называют отношением
показывает отношение?
двух
чисел?
Что
Отношением двух чисел называют результат от их
деления друг на друга, то есть это частное этих чисел.

3.

ПОВТОРИМ!
Что называют отношением
показывает отношение?
двух
чисел?
Отношение двух чисел показывает:
во сколько раз одно число больше
другого;
какую часть одно число составляет от другого.
Что

4.

ПОВТОРИМ!
AB : CD = 2 : 7. О чём это говорит?
Длина отрезка AB составляет
или
длины отрезка CD.
Разделить число в заданном отношении — значит
разбить его на части, пропорциональные заданным
числам. Длина AB - это 2 части, а длина CD - это 7
таких же частей.

5.

ПОВТОРИМ!
В ΔАВС АВ : ВС : АС = 2 : 4 : 3, РАВС = 45 дм.
Найдите стороны треугольника АВС.
Что называют пропорцией?
Верны ли пропорции:

6.

ПОВТОРИМ!
В пропорции a : b = c : d укажите крайние и средние
члены. Сформулируйте основное свойство пропорции.
Найдите неизвестный член пропорции:

7.

РАБОТАЕМ В ТЕТРАДИ
Отношение отрезков АВ и CD называется отношением
их длин, т.е. АВ : CD или
Отрезки АВ и CD пропорциональны
отрезкам А1В1 и C1D1, если
Пропорциональны ли отрезки АВ, А1В1 и CD, C1D1,
если АВ = 5 см, CD = 7 см, А1В1 = 7,5 см, C1D1 = 10,5
см?

8.

равенство верное, поэтому
отрезки пропорциональны.
Понятие пропорциональности
большего числа отрезков.
вводится
и
для
Три отрезка AB, CD и EF пропорциональны трём
отрезкам А1В1, C1D1, и E1F1

9.

РАБОТАЕМ В ТЕТРАДИ
Отрезки AB, CD, MN пропорциональны отрезкам
А1В1, C1D1, M1N1. Найдите C1D1 и MN, если AB = 5
см, А1В1 = 4 см, CD = 6 см, M1N1 = 8 см.
из первого и второго отношения найдём, что C1D1 = 4,8 см.

10.

РАБОТАЕМ В ТЕТРАДИ
Отрезки AB, CD, MN пропорциональны отрезкам
А1В1, C1D1, M1N1. Найдите C1D1 и MN, если AB = 5
см, А1В1 = 4 см, CD = 6 см, M1N1 = 8 см.
приравняем первое и третье отношение, найдём MN = 10 см.

11.

РАБОТА ПО ТЕМЕ УРОКА
В повседневной жизни встречаются
одинаковой формы, но разных размеров:
теннисный мяч и
футбольный мяч
коробки
различного объёма
предметы
фотографии
разного формата

12.

РАБОТА ПО ТЕМЕ УРОКА
В геометрии фигуры одинаковой формы принято
называть подобными.
теннисный мяч и
футбольный мяч
коробки
различного объёма
фотографии
разного формата

13.

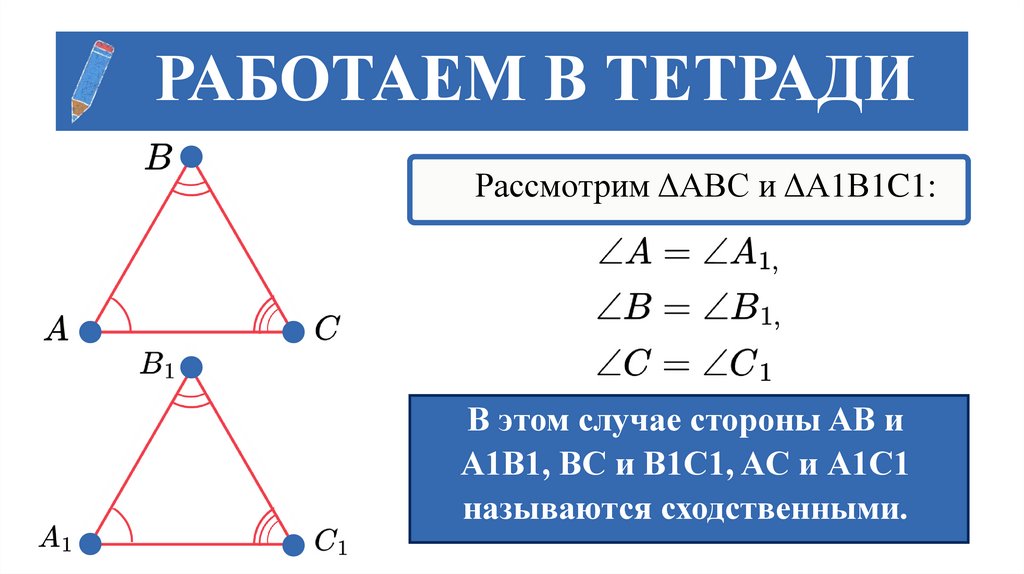
РАБОТАЕМ В ТЕТРАДИ
Рассмотрим ΔАВС и ΔА1В1C1:
В этом случае стороны AB и
А1В1, BC и B1C1, AC и А1C1
называются сходственными.

14.

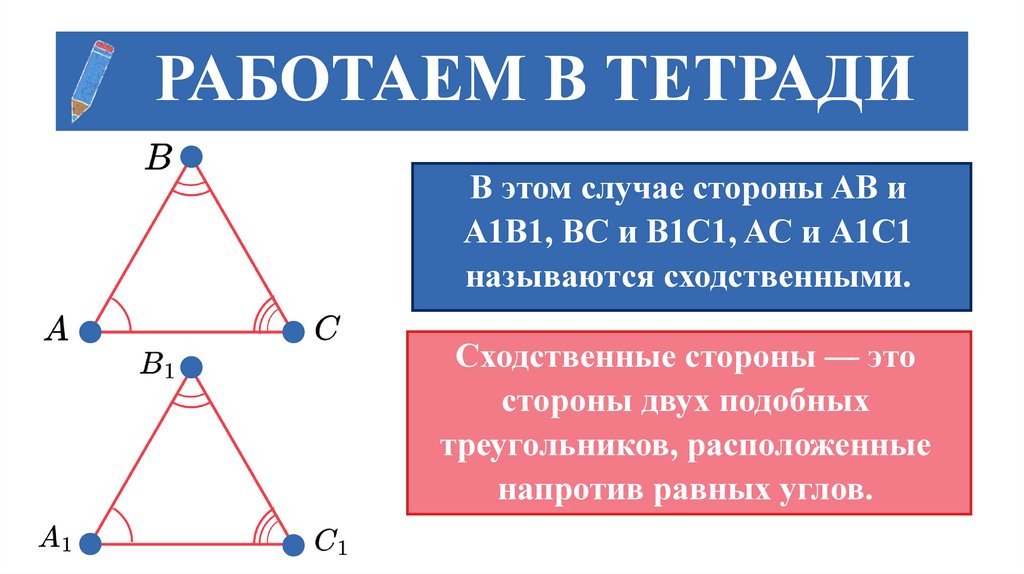
РАБОТАЕМ В ТЕТРАДИ
В этом случае стороны AB и
А1В1, BC и B1C1, AC и А1C1
называются сходственными.
Сходственные стороны — это
стороны двух подобных
треугольников, расположенные
напротив равных углов.

15.

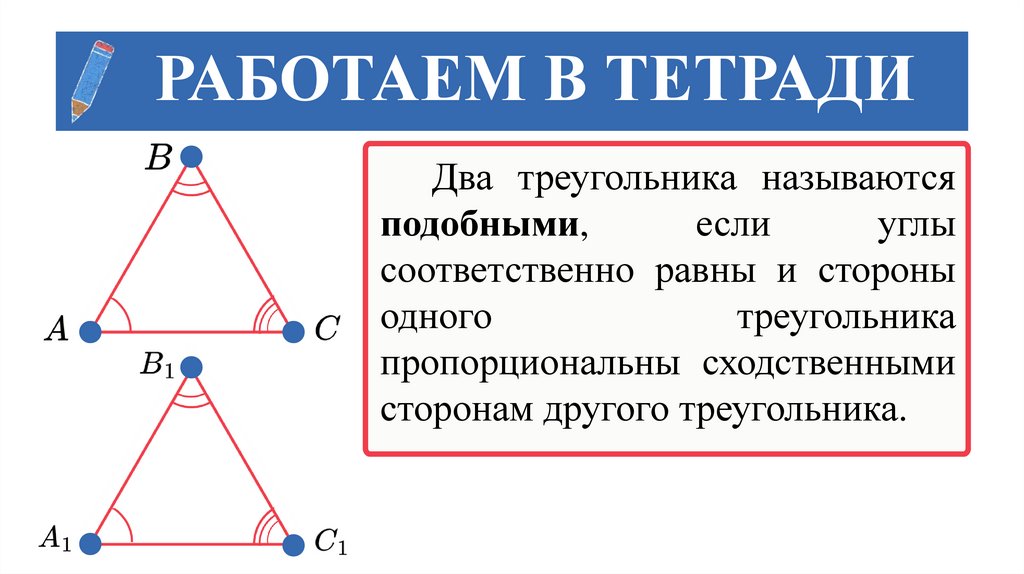
РАБОТАЕМ В ТЕТРАДИ
Два треугольника называются
подобными,
если
углы
соответственно равны и стороны
одного
треугольника
пропорциональны сходственными
сторонам другого треугольника.

16.

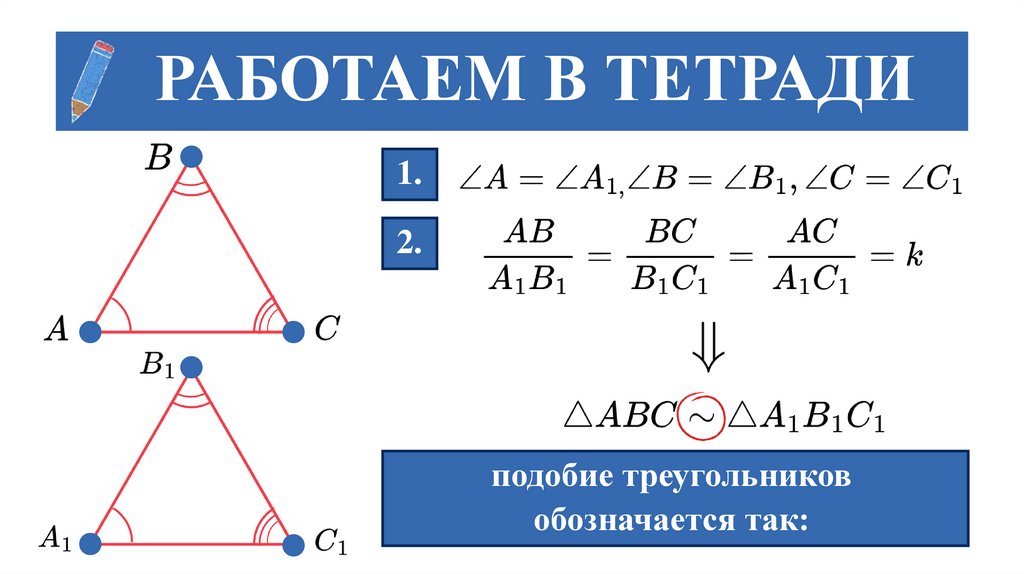
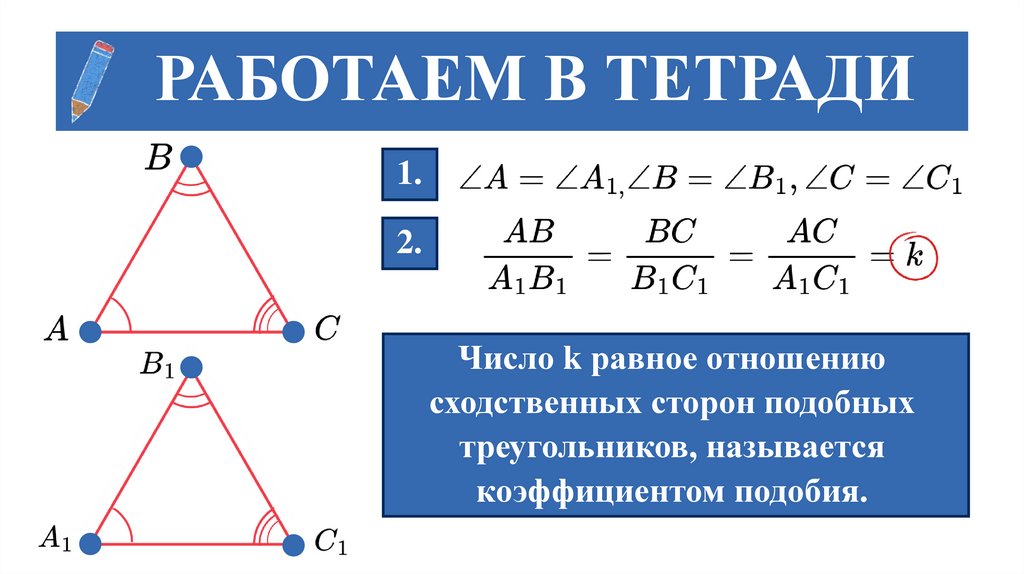
РАБОТАЕМ В ТЕТРАДИ
1.
2.
подобие треугольников
обозначается так:

17.

РАБОТАЕМ В ТЕТРАДИ
1.
2.
Число k равное отношению
сходственных сторон подобных
треугольников, называется
коэффициентом подобия.

18.

ДОМА
Учить записи № 641