Similar presentations:
Подобные треугольники (8 класс)
1.
2.
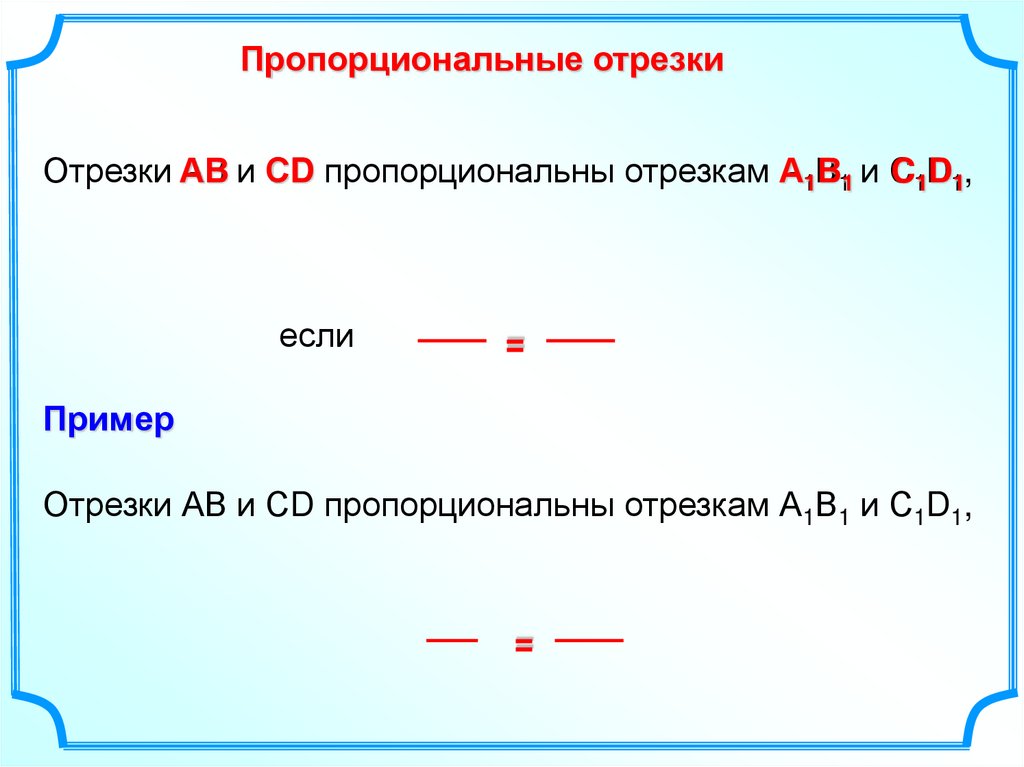
Пропорциональные отрезкиОтрезки АВ и СD пропорциональны отрезкам А1В11 и С
C1D1,
если
=
Пример
Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1,
=
3.
Понятие пропорциональности вводится и для большегочисла отрезков.
Отрезки
АВ,
СD и EF пропорциональны отрезкам А1В11, С
АВ СD
C11D11 и E
E11FF11,
если
=
=
4. Подобные фигуры
Предметы одинаковойформы, но разных
размеров
Фотографии, отпечатанные
с одного негатива, но с
разными увеличениями;
Здание и его макет
Планы,
географические
карты одного и того
же района,
выполненные в
разных масштабах.
5.
6.
7.
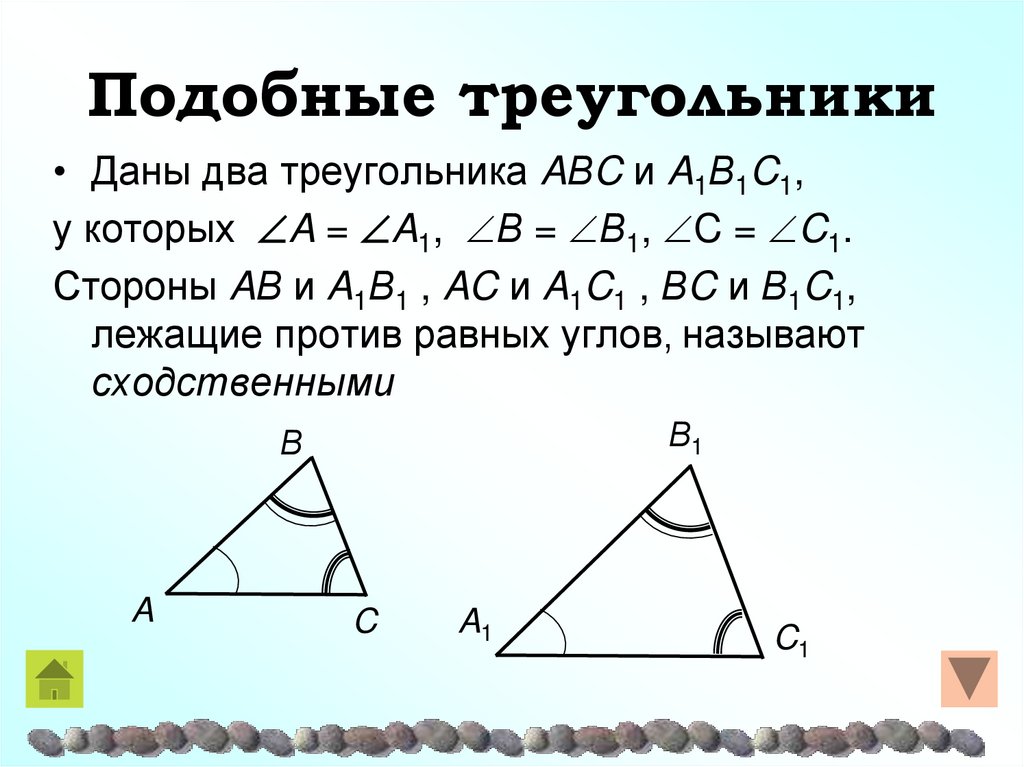
Подобными являются любые два круга, два квадрата.8. Подобные треугольники
• Даны два треугольника AΒC и A1Β1C1,у которых A = A1, Β = Β1, C = C1.
Стороны AΒ и A1Β1 , AC и A1C1 , ΒC и Β1C1,
лежащие против равных углов, называют
сходственными
Β1
Β
A
C
A1
C1
9.
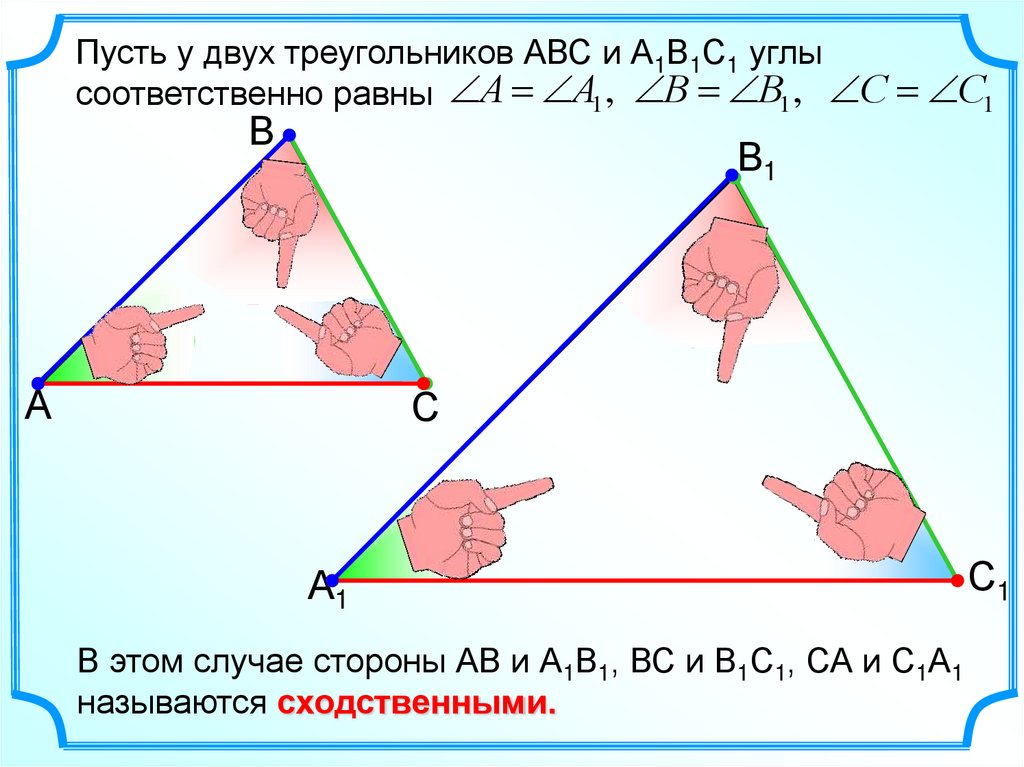
Пусть у двух треугольников АВС и А1В1С1 углысоответственно равны А А1 , В В1 , С С1
В
В1
А
С
А1
В этом случае стороны АВ и А1В1, ВС и В1С1, СА и С1А1
называются сходственными.
С1
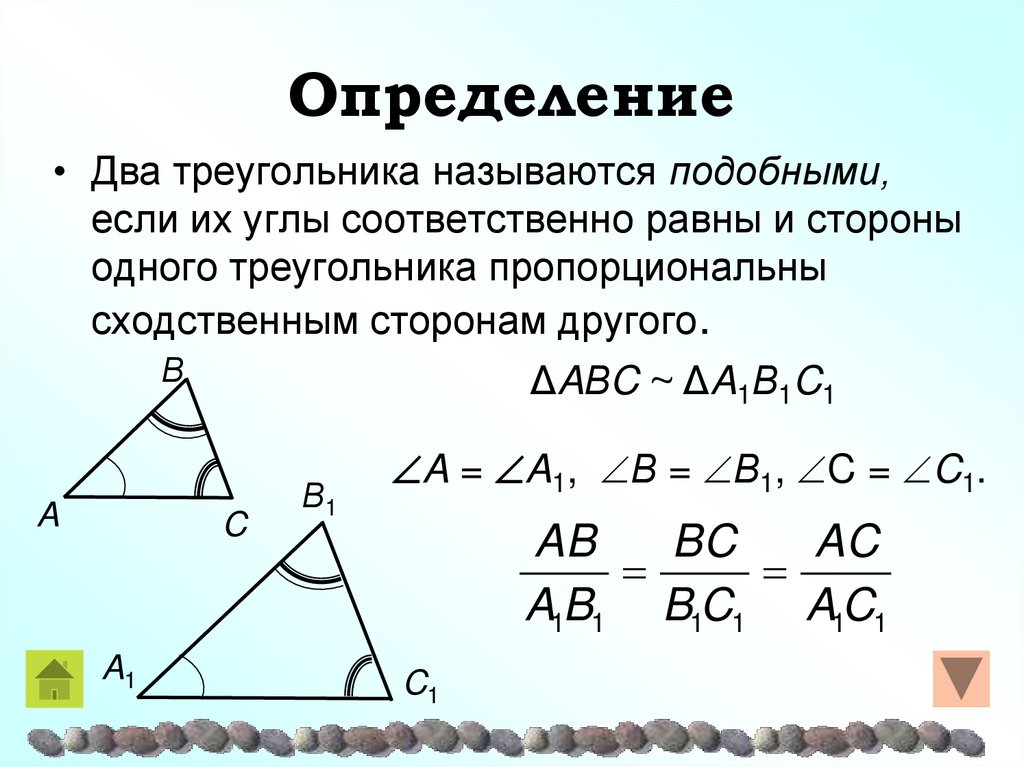
10. Определение
• Два треугольника называются подобными,если их углы соответственно равны и стороны
одного треугольника пропорциональны
сходственным сторонам другого.
Β
ΔAΒC ~ ΔA1Β1C1
A
C
A1
Β1
A = A1, Β = Β1, C = C1.
AB
BC
AC
A1B1 B1C1 A1C1
C1
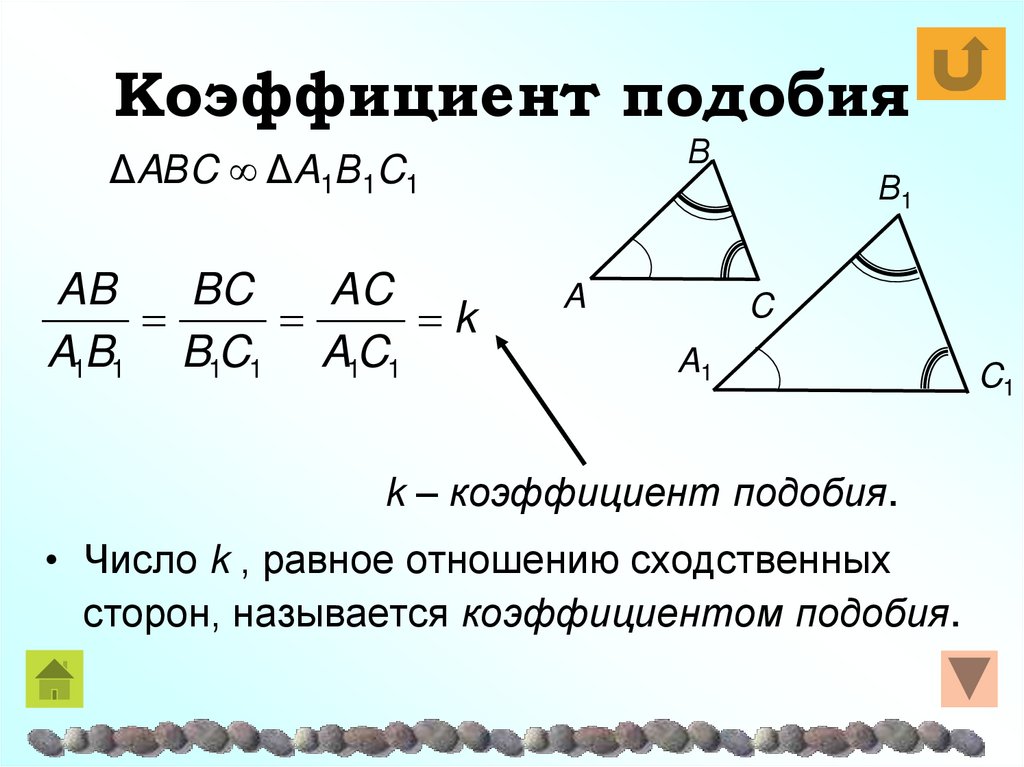
11. Коэффициент подобия
ΒΔAΒC ∞ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
Β1
C
A1
k – коэффициент подобия.
• Число k , равное отношению сходственных
сторон, называется коэффициентом подобия.
C1
12. Дополнительные свойства
Отношение высот подобных треугольников,проведенных к сходственным сторонам,
равно коэффициенту подобия.
Отношение медиан подобных треугольников,
проведенных к сходственным сторонам,
равно коэффициенту подобия.
Отношение биссектрис подобных
треугольников, проведенных к сходственным
сторонам, равно коэффициенту подобия.
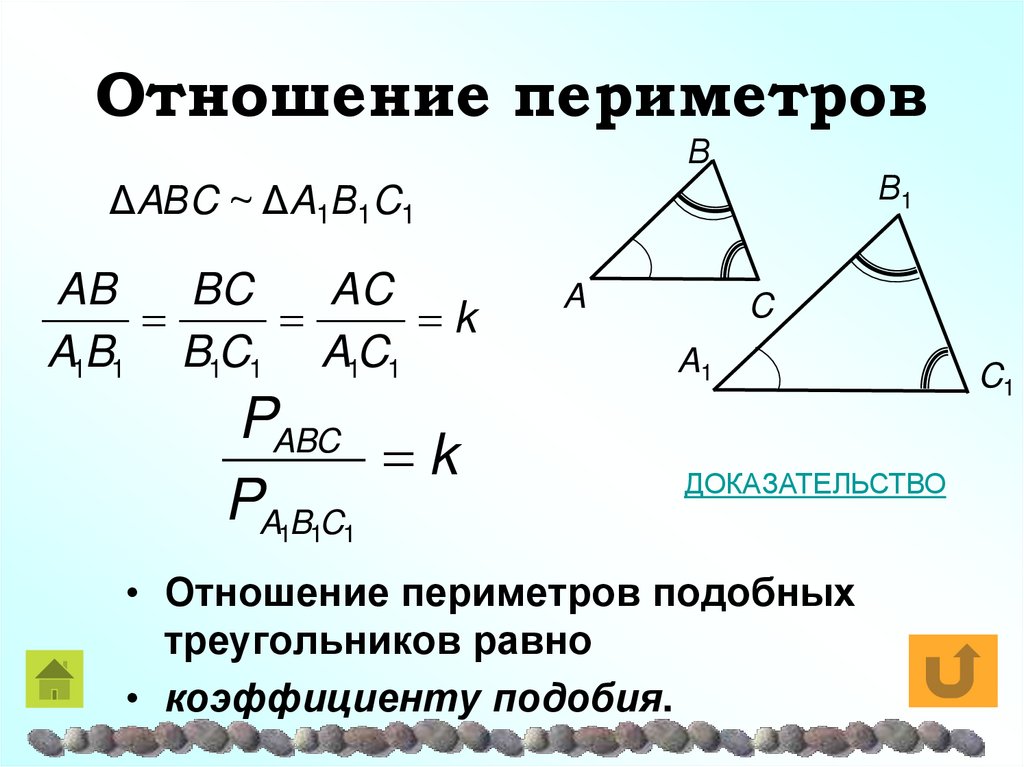
13. Отношение периметров
ΒΒ1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
PABC
k
PA1B1C1
A
C
A1
ДОКАЗАТЕЛЬСТВО
• Отношение периметров подобных
треугольников равно
• коэффициенту подобия.
C1
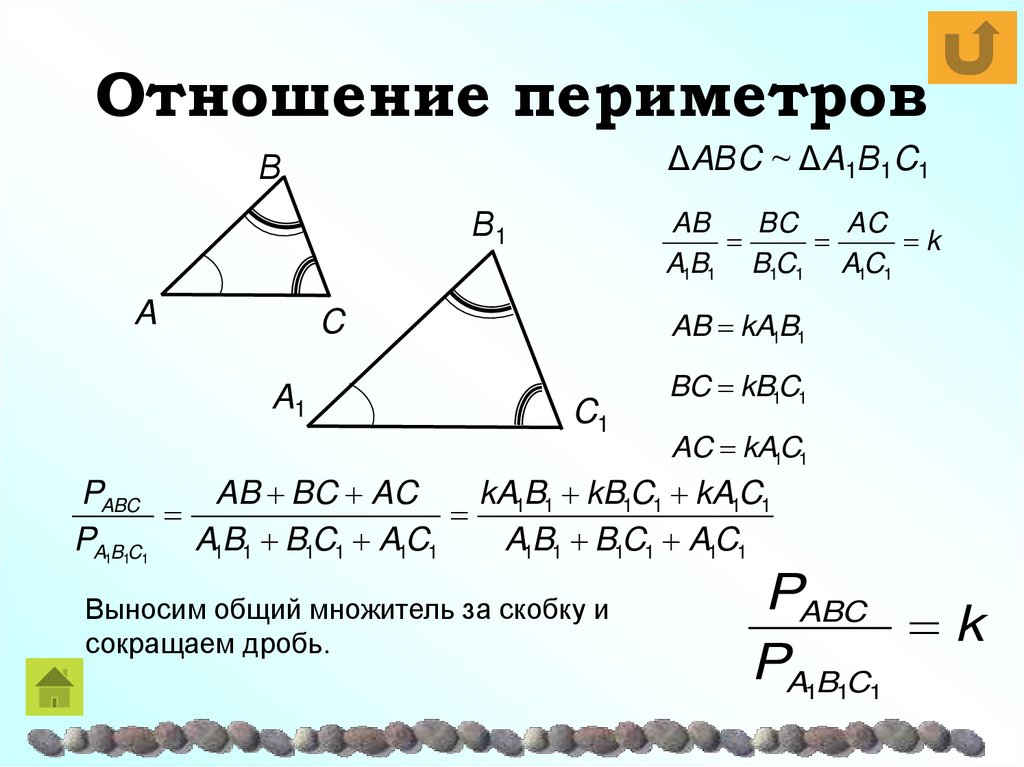
14. Отношение периметров
ΔAΒC ~ ΔA1Β1C1Β
Β1
A
AB
BC
AC
k
A1B1 B1C1 A1C1
AB kA1B1
C
A1
C1
BC kB1C1
AC kA1C1
PABC
AB BC AC
kA1B1 kB1C1 kA1C1
PA1B1C1 A1B1 B1C1 A1C1
A1B1 B1C1 A1C1
Выносим общий множитель за скобку и
сокращаем дробь.
PABC
k
PA1B1C1
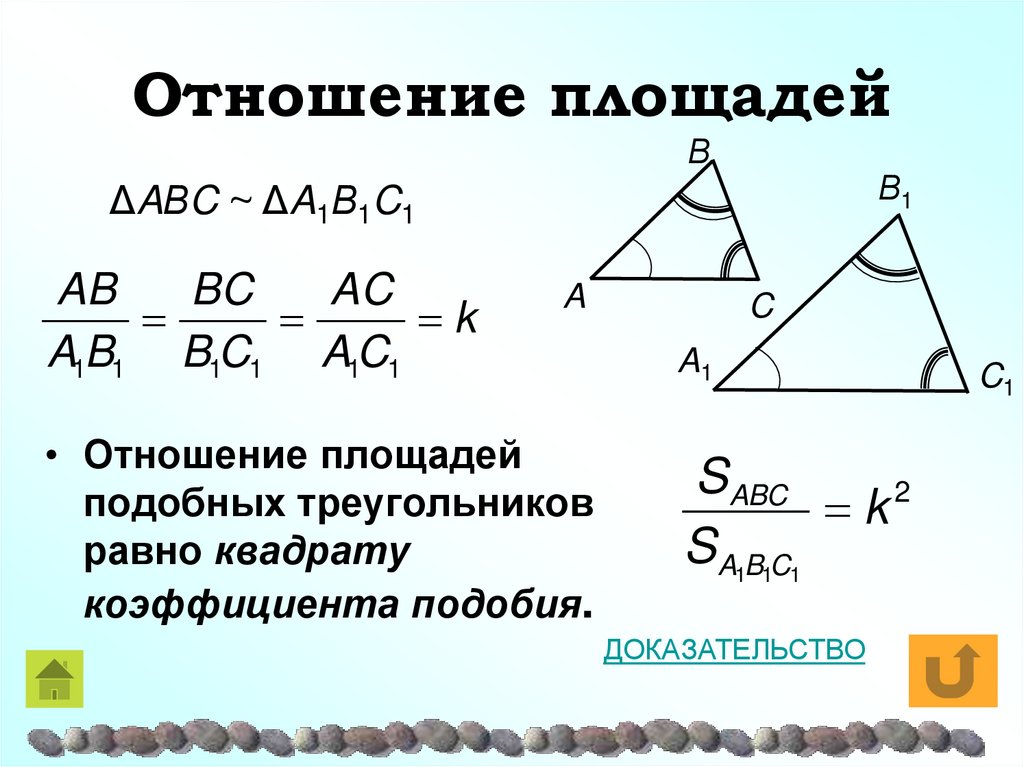
15. Отношение площадей
ΒΒ1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
• Отношение площадей
подобных треугольников
равно квадрату
коэффициента подобия.
C
A1
S ABC
2
k
SA1B1C1
ДОКАЗАТЕЛЬСТВО
C1
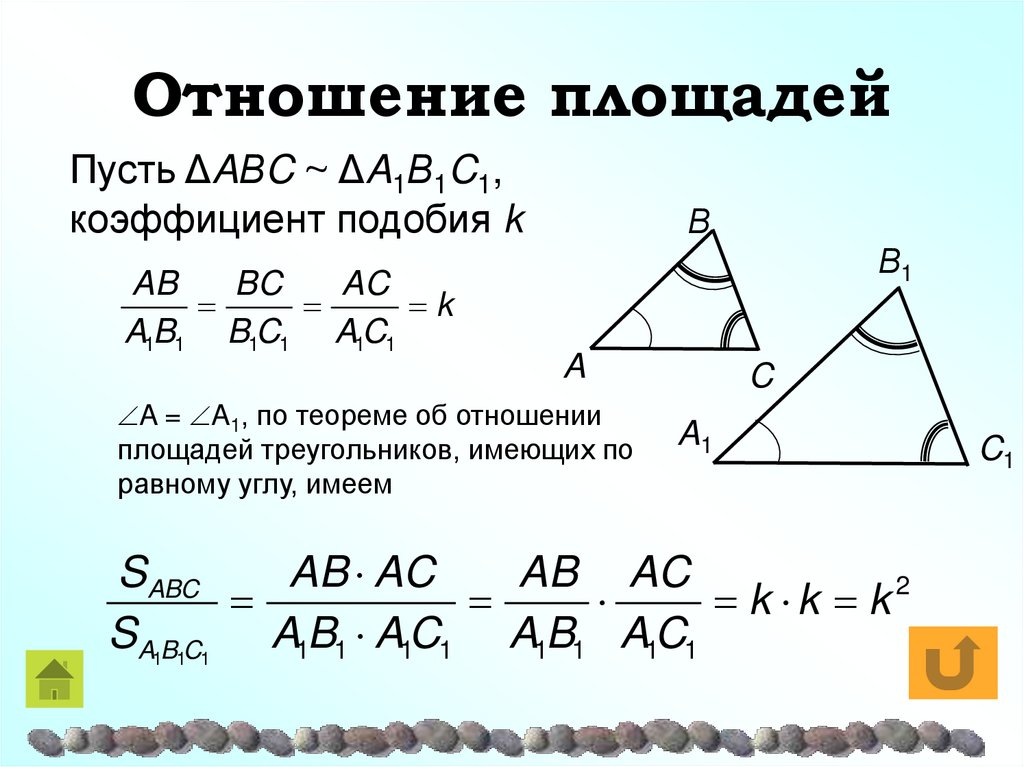
16. Отношение площадей
Пусть ΔAΒC ~ ΔA1Β1C1,коэффициент подобия k
AB
BC
AC
k
A1B1 B1C1 A1C1
Β
Β1
A
A = A1, по теореме об отношении
площадей треугольников, имеющих по
равному углу, имеем
C
A1
SABC
AB AC
AB AC
k k k2
SA1B1C1 A1B1 A1C1 A1B1 A1C1
C1
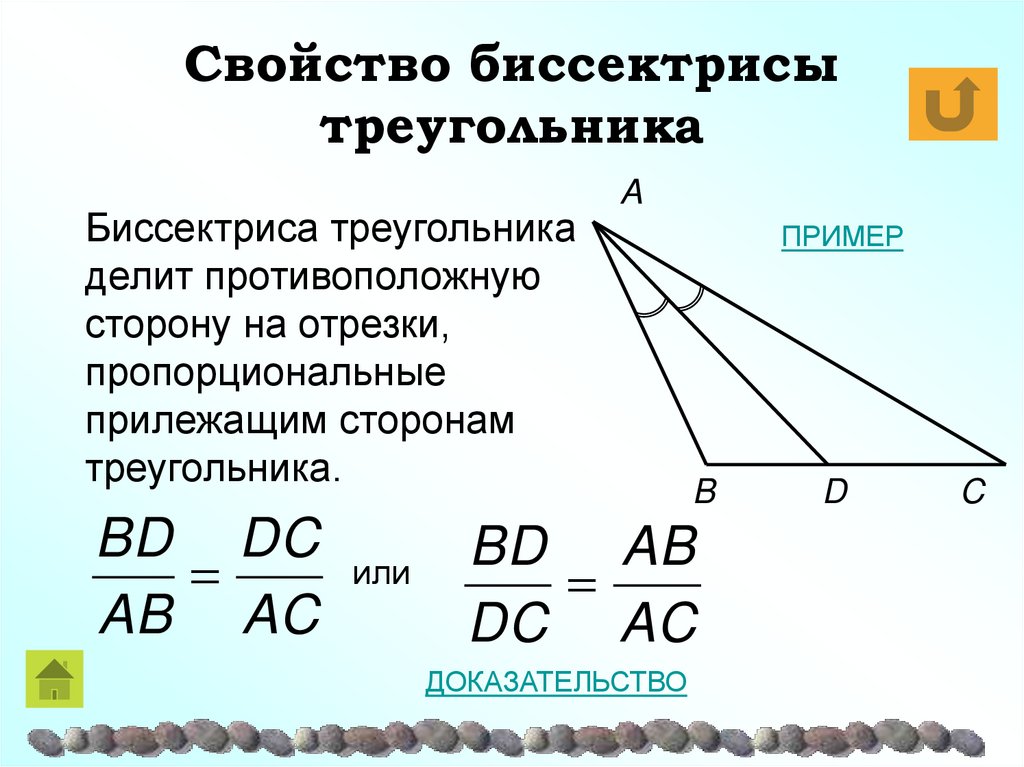
17. Свойство биссектрисы треугольника
Биссектриса треугольникаделит противоположную
сторону на отрезки,
пропорциональные
прилежащим сторонам
треугольника.
BD DC
или
AB AC
A
ПРИМЕР
B
BD AB
DC AC
ДОКАЗАТЕЛЬСТВО
D
C
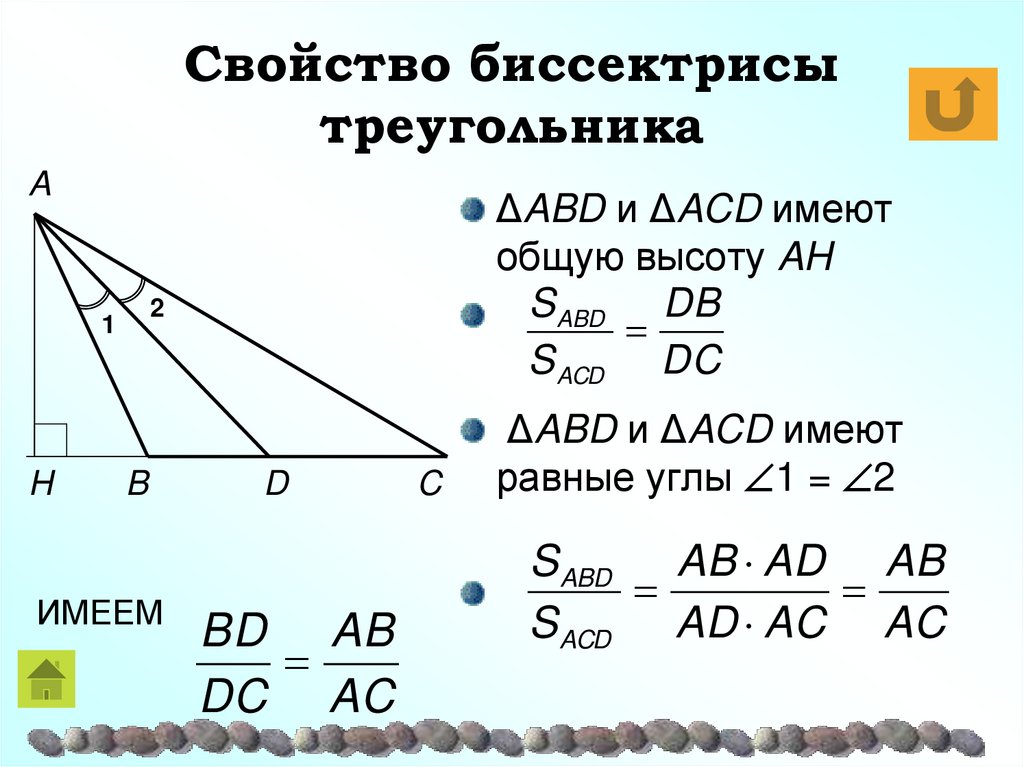
18. Свойство биссектрисы треугольника
A2
1
H
ΔABD и ΔACD имеют
общую высоту AH
S ABD DB
S ACD DC
B
ИМЕЕМ
D
BD AB
DC AC
C
ΔABD и ΔACD имеют
равные углы 1 = 2
S ABD AB AD AB
S ACD AD AC AC
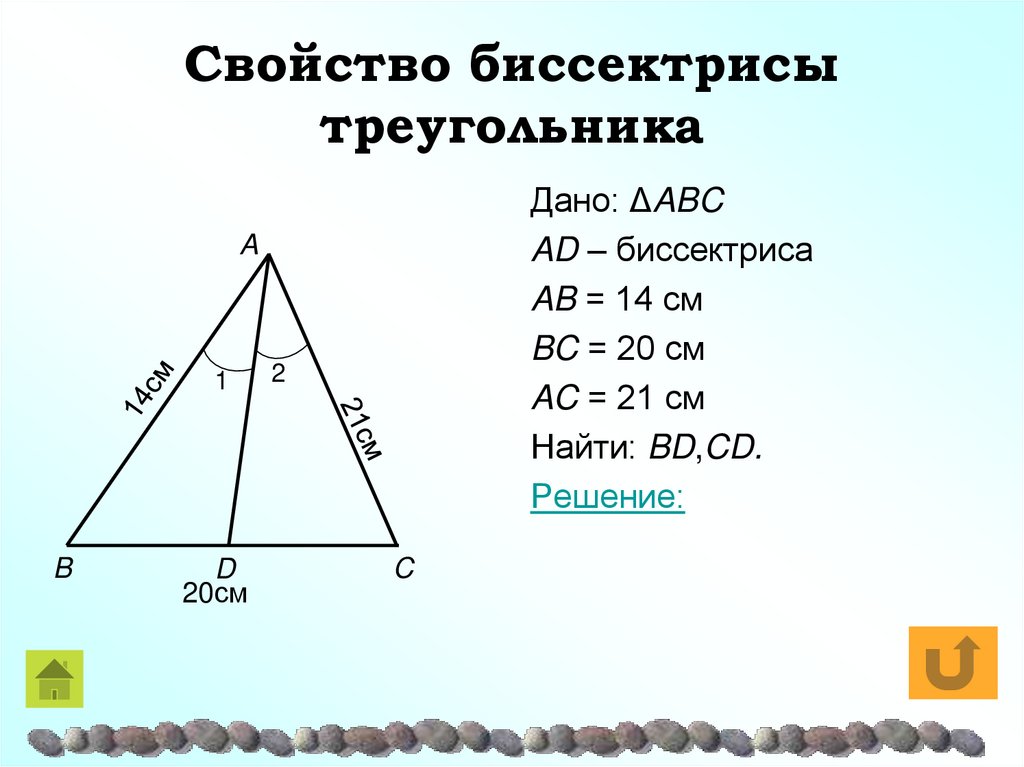
19. Свойство биссектрисы треугольника
Дано: ΔABCAD – биссектриса
AB = 14 см
BC = 20 см
AC = 21 см
Найти: BD,CD.
Решение:
A
1
B
D
20см
2
C
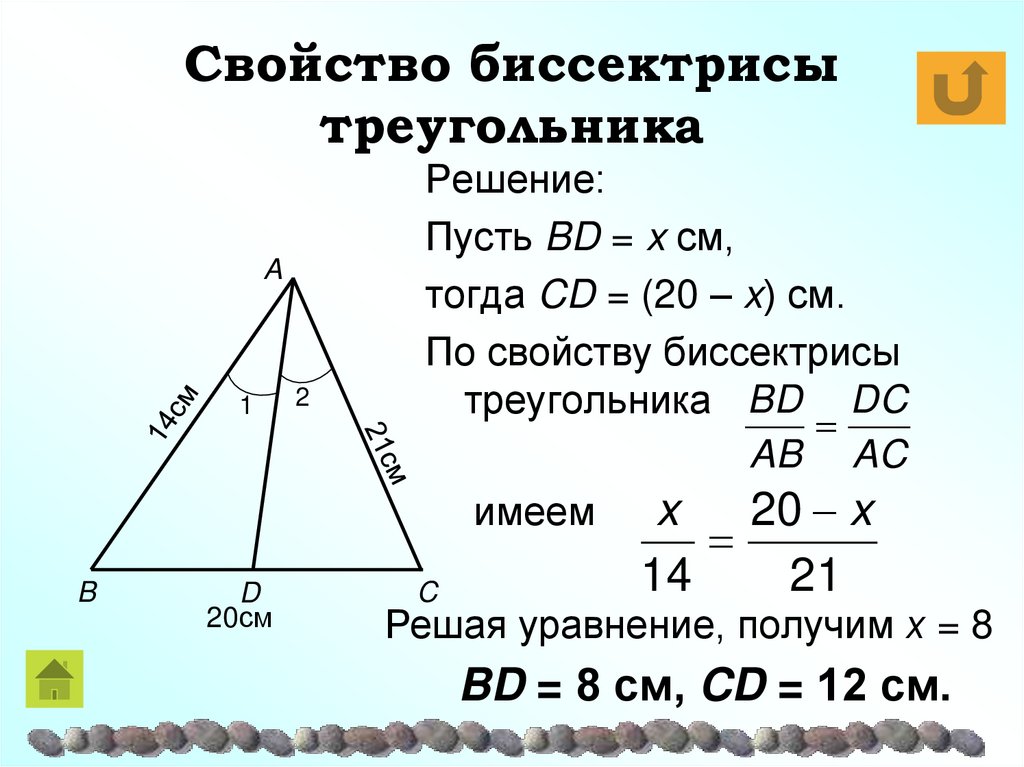
20. Свойство биссектрисы треугольника
A1
B
D
20см
2
Решение:
Пусть BD = x см,
тогда CD = (20 – x) см.
По свойству биссектрисы
треугольника BD DC
AB AC
имеем
x
20 x
C
14
21
Решая уравнение, получим х = 8
BD = 8 см, CD = 12 см.
21.
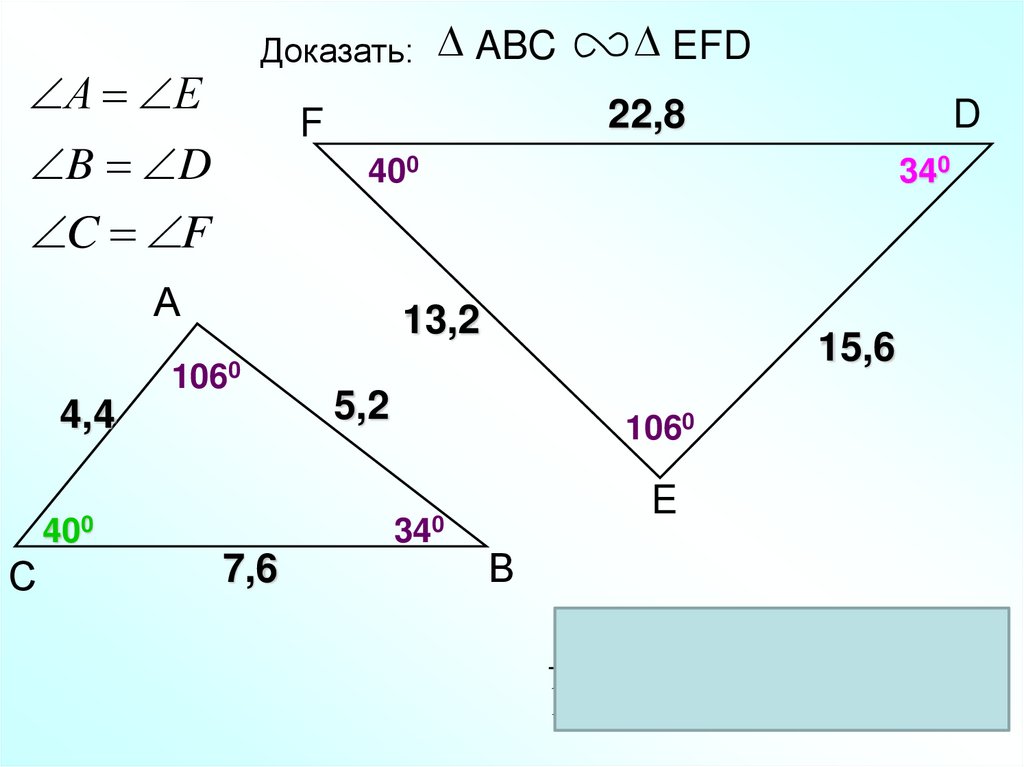
Доказать: ABCА Е
22,8
F
B D
C F
D
400
А
340
13,2
1060
4,4
400
С
EFD
5,2
1060
340
7,6
15,6
E
В
5,2
7 ,6
4,4
Верно
13,2 15,6 22,8
22.
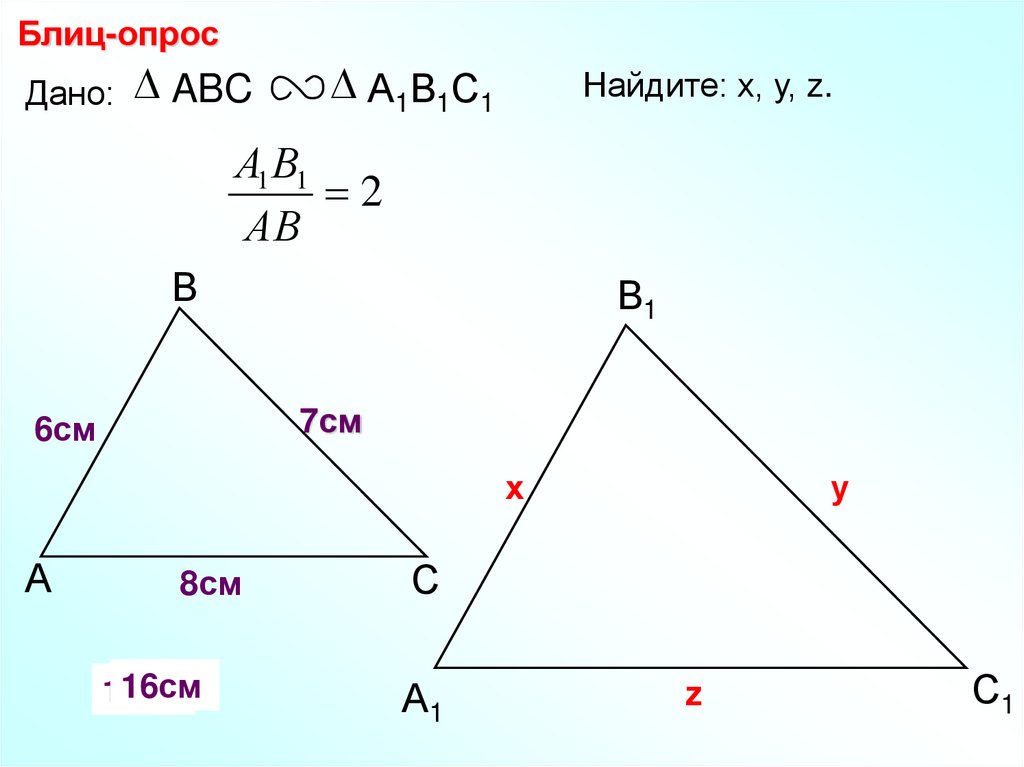
Блиц-опросДано: ABC
А1В1С1
Найдите: х, у, z.
А1 В1
2
АВ
В
В1
7см
6см
х
А
8см
16см
14см
12см
у
С
А1
z
С1
23.
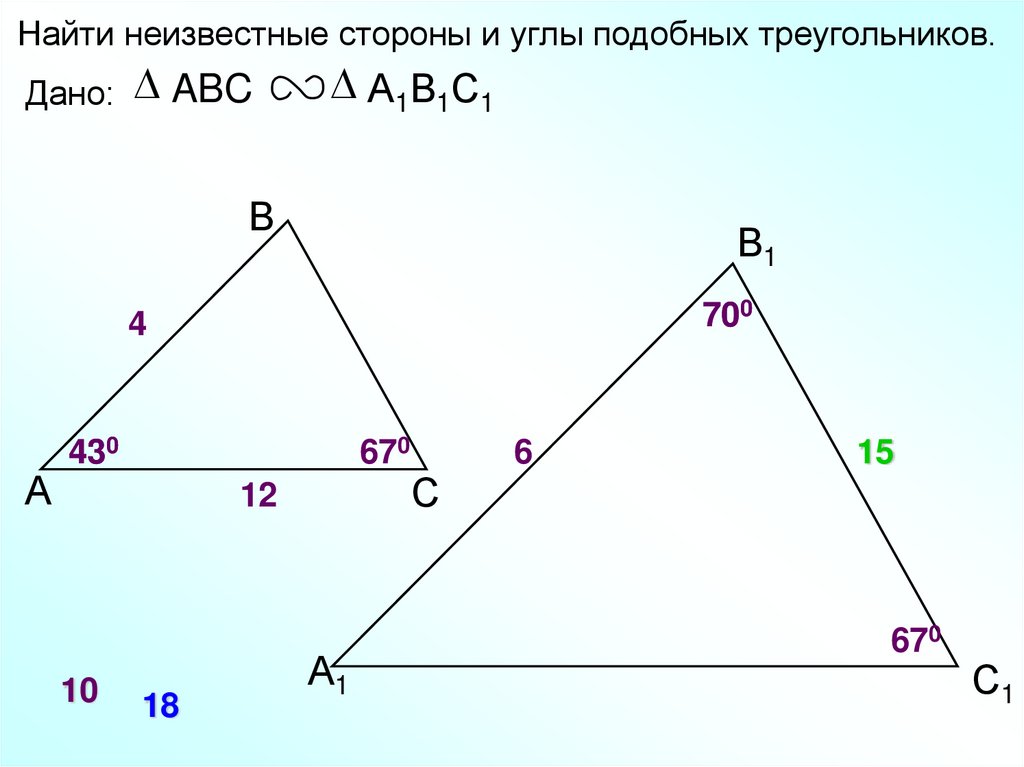
Найти неизвестные стороны и углы подобных треугольников.Дано: ABC
А1В1С1
В
В1
700
4
А
430
670
12
10
18
А1
С
6
15
670
С1
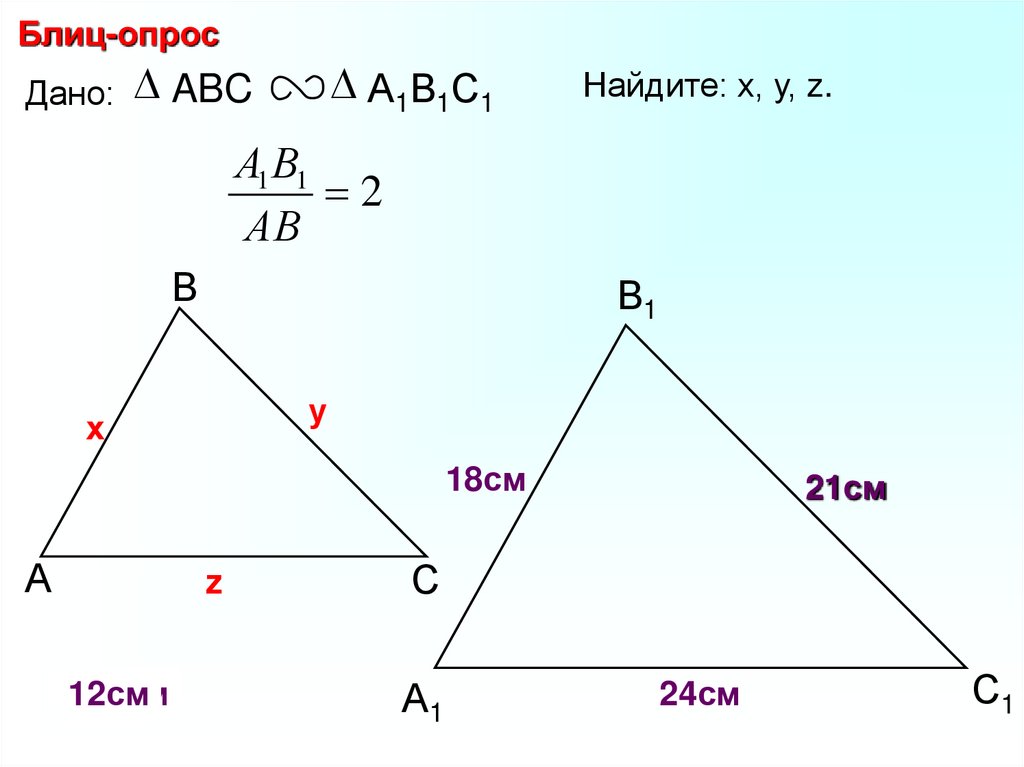
24.
Блиц-опросДано: ABC
А1В1С1
Найдите: х, у, z.
А1 В1
2
АВ
В
В1
у
х
18см
А
z
10,5см
12см
9см
21см
С
А1
24см
С1
25.
Блиц-опросДано: ABC
А1В1С1
В
Найдите: х, у.
В1
6см
7см
х
18см
А
8см
С
А1
24см
21см
у
С1
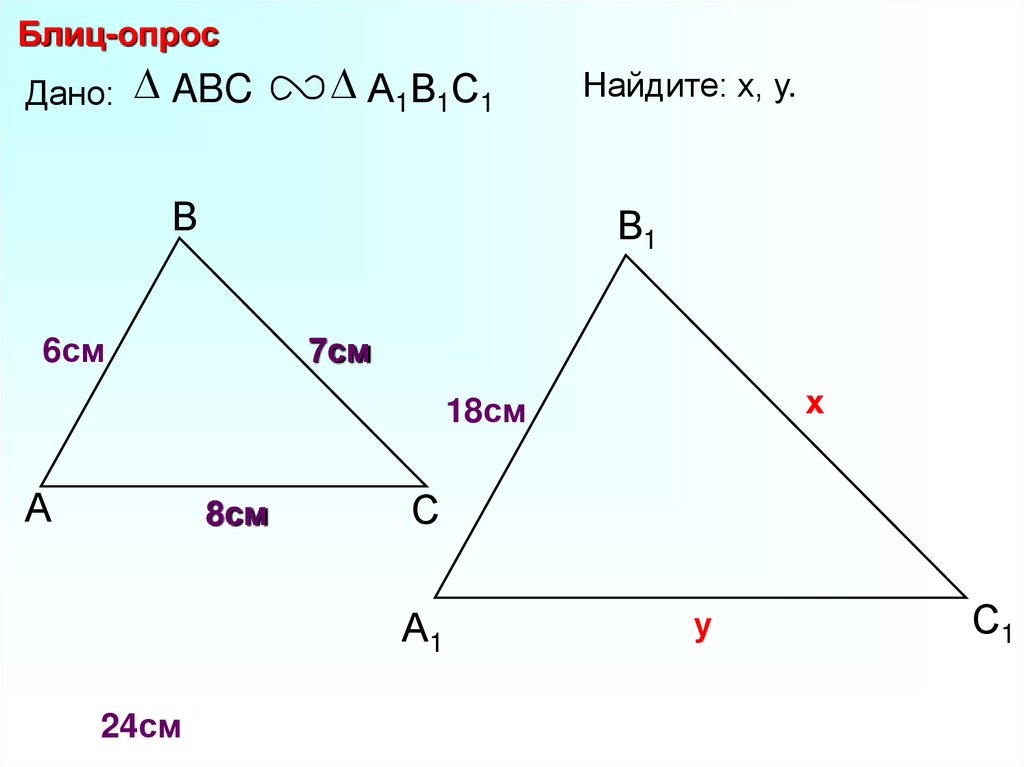
26.
Блиц-опросДано: ABC
А1В1С1
Найдите: х, у.
В1
В
6см
А
12см
х
8см
16см 7см
С
А1
14см
у
С1
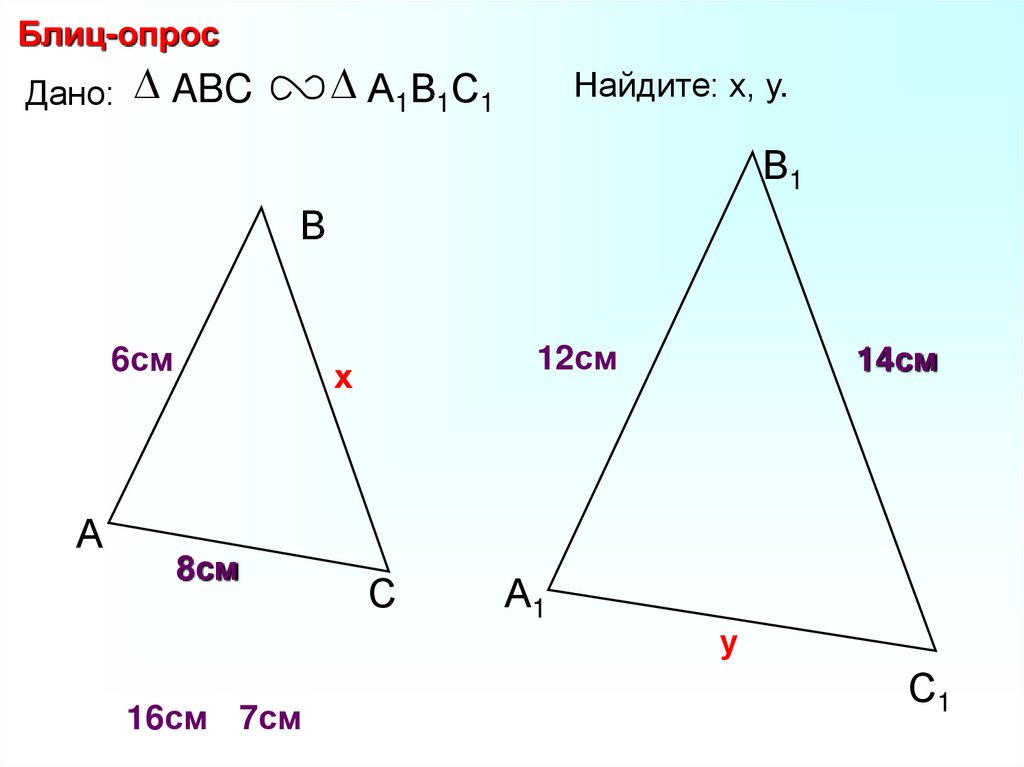
27.
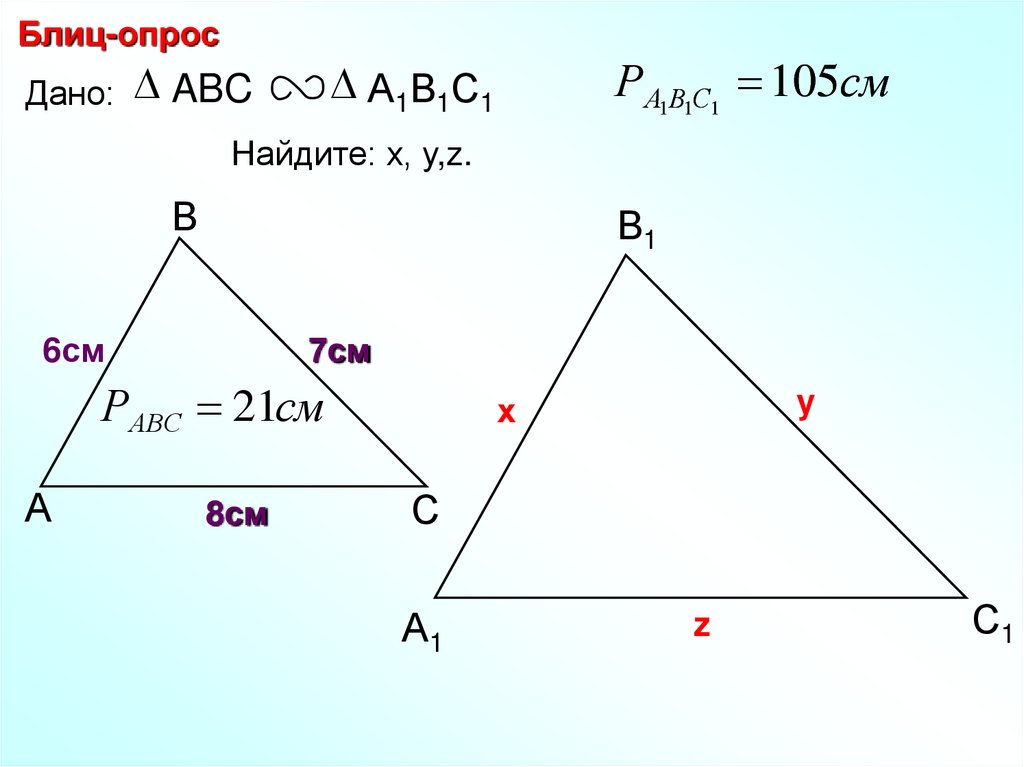
Блиц-опросДано: ABC
РА1В1С1 105см
А1В1С1
Найдите: х, у,z.
В
В1
6см
7см
РАВС 21см
А
8см
y
х
С
А1
z
С1






 mathematics
mathematics








