КДД_ФОМНЭ_2023_№ 3

1. ФИЗИЧЕСКИЕ ОСНОВЫ МИКРО- И НАНОЭЛЕКТРНИКИ

Лекция 3
ФАКУЛЬТЕТ ЭЛЕКТРОНИКИ
11.03.04 – Электроника и
наноэлектроника

2.

Вырожденные и невырожденные коллективы микрочастиц
По характеру поведения в коллективе все микрочастицы делятся на фермионы
и бозоны. Фермионы (электроны, протоны, нейтроны и т.д.) обладают полуцелым
спином (ħ/2, 3ħ/2,…) характеризуются стремлением к "уединению". Если данное
состояние уже занято фермионом, то никакой другой фермион не сможет
попасть в это состояние (принцип запрета Паули). Бозоны (фотоны)
обладают целочисленным спином (0, ħ, 2ħ, …), характеризуются стремлением к "объединению". Они могут неограниченно заселять одно и то же состояние. Специфическое
"отталкивание" фермионов и "притяжение" бозонов называют обменным взаимодействием.
Влияние специфики частиц (фермионов и бозонов) на свойства коллектива как целого
будет проявляться, если микрочастицы "встречаются" друг с другом достаточно часто, т.е.
попадают в одно и тоже состояние квантовое состояние.
Предположим, что N одинаковых частиц распределены по G различным состояниям.
"Частота встреч" характеризуется отношением N/G. Микрочастицы встречаются редко, если
выполняется условие:
N/G << 1.
(1)
В этих условиях специфика фермионов и бозонов проявляться не может, поскольку
вероятность заселения одного и того же состояния несколькими частицами практически не
возникает. В этом случае свойства коллектива как целого не будут зависеть от специфики
микрочастиц, из которых он состоит. Такие коллективы называются невырожденными, а
условие (1) – условием невырожденности.
Если же число частиц N сравнимо с числом состояний G, т.е. выполняется условие:
N/G ≈ 1,
(2)
то специфика микрочастиц будет оказывать значительное влияние на свойства коллектива.
Такие коллективы называются вырожденными.

3.

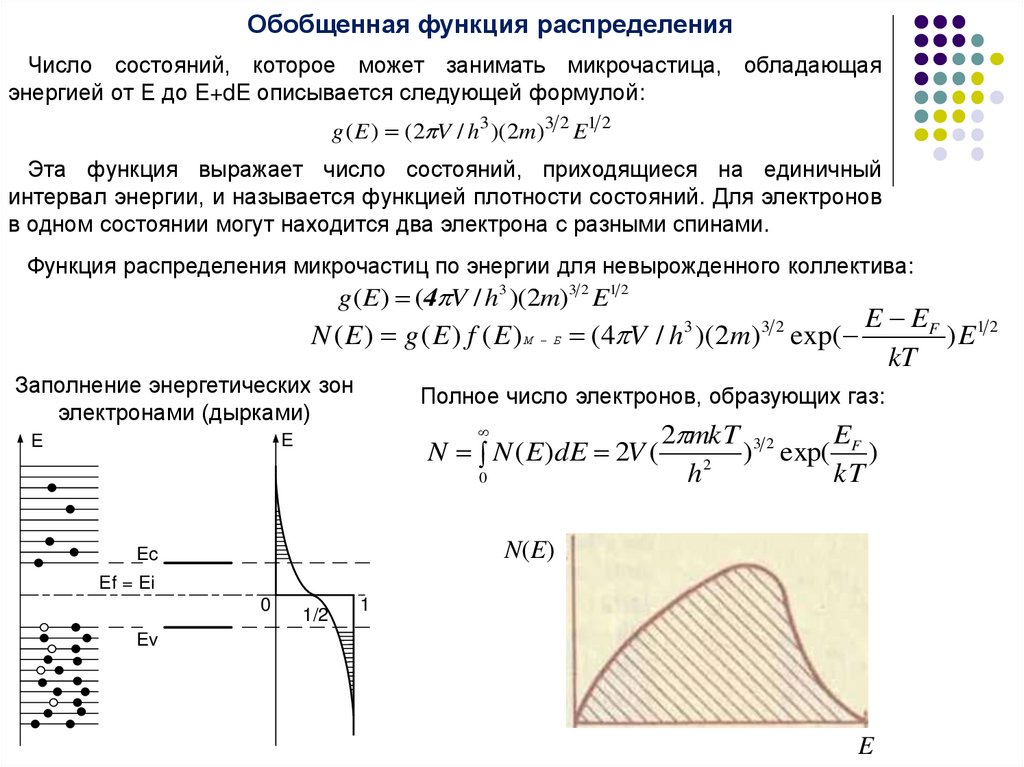
Плотность энергетических состояний
Для описания состояний микрочастиц используют
шестимерное
пространство координат - импульсов. Пространственная локализация
микрочастицы в данном пространстве определяется соотношением
неопределенностей Гейзенберга.