Similar presentations:
1_1 Матрицы
1.
Раздел 5. МАТРИЦЫ ИОПРЕДЕЛИТЕЛИ. СИСТЕМЫ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ
УРАВНЕНИЙ
2.
§ 1. Матрицы: основные понятия идействия с матрицами
Опр.1. Матрицей размера m×n называется прямоугольная
таблица чисел (или других математических объектов) –
элементов матрицы, расположенных в m строках и n столбцах:
aij – элемент, стоящий на пересечении i-й строки и j-го
столбца матрицы; числа i, j называются индексами этого
элемента.
Краткая запись:
A aij
m n
или
A aij
m n
.
3.
Джеймс Джозеф Сильвестр4.
Опр. 2. Две матрицы называются равными, еслиони имеют одинаковые размеры и все их
соответствующие элементы равны.
Опр. 3. Нулевая матрица – матрица, у которой все
элементы равны нулю.
0 0 0
Например, O2 3 0 0 0 –
нулевая матрица размера 2×3.
Опр. 4. Матрица, у которой количество строк равно
количеству столбцов (и равно n), называется
квадратной матрицей порядка n.
Побочная
диагональ
Главная
диагональ
5.
Опр.5.Квадратная
матрица
называется
диагональной, если все ее элементы вне главной
диагонали равны нулю.
Опр.6. Диагональная матрица, у которой все
элементы главной диагонали равны 1, называется
единичной.
Единичная матрица обозначается En или In.
Например,
3-го порядка.
– единичная матрица
6.
Основные операции над матрицамиОпр. 7. Суммой матриц A aij m nи B bij
одного и
m n
того же размера называется матрица C cij
такого
m n
же размера, элементы которой равны сумме
соответствующих элементов матриц A и B, т. е.
cij aij bij (1 i m,1 j n).
1 2 1
2 1 0
, B
.
Пример 1. Пусть A
0 2 3
3 2 5
7.
Свойства операции сложения матриц.1. A + B = B + A (коммутативность).
2. A +(B + C) = (A +B) + C (ассоциативность).
3. Am×n + Om×n = Am×n.
8.
Опр. 8. Произведением матрицына
A aij
m n
число называется матрица C cij
такого же
m n
размера, элементы которой равны соответствующим
элементам матрицы A, умноженным на , т. е.
cij aij (1 i m,1 j n).
Пример 2.
9.
Свойства операции умножения матрицы на число.10.
Опр. 9. Произведением матрицы A aijматрицу B bij
s n
m s
размера m s на
размера s n называется матрица C cij
m n
размера m n, элементы которой равны
cij ai1b1 j ai 2b2 j aisbsj (1 i m,1 j n),
т. е. чтобы получить элемент cij , стоящий в i-й строке и j-м
столбце матрицы-произведения, нужно элементы i-й строки
матрицы A умножить на соответствующие элементы j-го столбца
матрицы B и полученные произведения сложить.
(Говорят, что матрицы умножаются по правилу «строка на
столбец».)
Замечание. Произведение С = AB матриц A и B существует,
если матрица A согласована с матрицей B в том смысле, что
число столбцов первой из них равно числу строк второй. (Из
того, что матрица A согласована с матрицей B, вообще говоря, не
следует, что матрица B согласована с матрицей A.)
11.
31 2 1
1 .
A
,
B
Пример 3. Пусть
3 2 5
5
ВА =
АВ =
12.
31 2 1
1 .
A
,
B
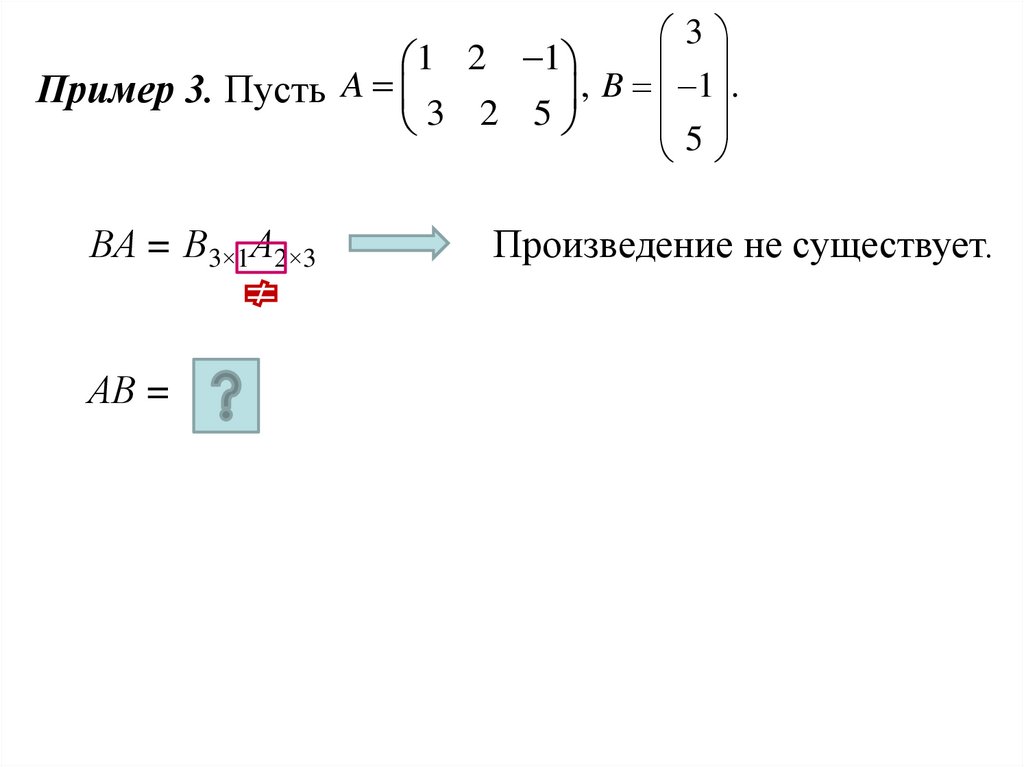
Пример 3. Пусть
3 2 5
5
ВА = В3×1А2×3
АВ =
Произведение не существует.
13.
31 2 1
1 .
A
,
B
Пример 3. Пусть
3 2 5
5
ВА = В3×1А2×3
АВ = А2×3В3×1=
Произведение не существует.
=
14.
31 2 1
1 .
A
,
B
Пример 3. Пусть
3 2 5
5
ВА = В3×1А2×3
АВ = А2×3В3×1=
Произведение не существует.
=
15.
1 21 2
.
,L
Пример 4. Пусть K
3 0
3 4
KL =
LK =
16.
1 21 2
.
,L
Пример 4. Пусть K
3 0
3 4
KL =
LK =
17.
1 21 2
.
,L
Пример 4. Пусть K
3 0
3 4
KL =
LK =
18.
1 21 2
.
,L
Пример 4. Пусть K
3 0
3 4
KL =
LK =
19.
1 21 2
.
,L
Пример 4. Пусть K
3 0
3 4
KL =
LK =
Этот пример показывает, что в общем случае
AB ≠ BA. Матрицы A и B, для которых AB = BA,
называются коммутирующими (перестановочными).
Упражнение 1. Что можно сказать о размерах
коммутирующих матриц?
20.
Свойства операции умножения матриц.1. Существуют матрицы, для которых AB ≠ BA.
(Умножение матриц не коммутативно.)
2. A(BC) = (AB)C (ассоциативность).
3. A(B + C) = AB +AC; (A + B)C = AC + BC
(дистрибутивность).
4. Am n En n Em m Am n Am n , где En n , Em m –
единичные матрицы соответствующих размеров.
21.
22
1 2
Упражнение 2. Вычислить 2 1 2 .
2 2 1
1 1
,
X Y
0 1
Упражнение 3. Решить систему
2 X 3Y 1 0 .
0 1
22.
Опр. 10. Матрица AT, полученная из матрицы Aзаменой каждой ее строки столбцом с тем же номером,
называется транспонированной к матрице A.
Если исходная матрица имеет размер m×n, то
транспонированная к ней будет иметь размер n×m.
4 1
4 0 5
0 3 ;
T
Пример 5. Если A2 3
,
A
то 3 2
1 3 2
5 2
4 3 8
4 6 2
если B 3 1 0 , то BT 6 1 5 .
2 0 1
8 5 1
23.
Свойства операции транспонирования матриц.1. (AT)T = A.
2. (A + B)T = A T + BT.
3. ( A)T = AT ( – число).
4. (AB)T = BTA T.










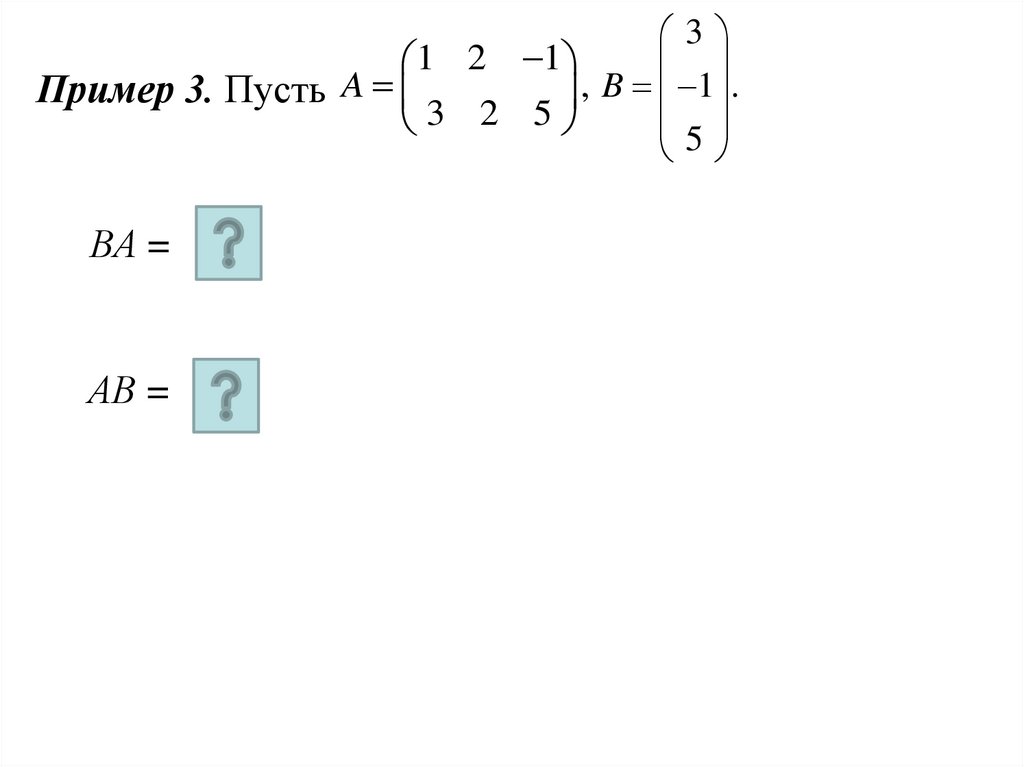


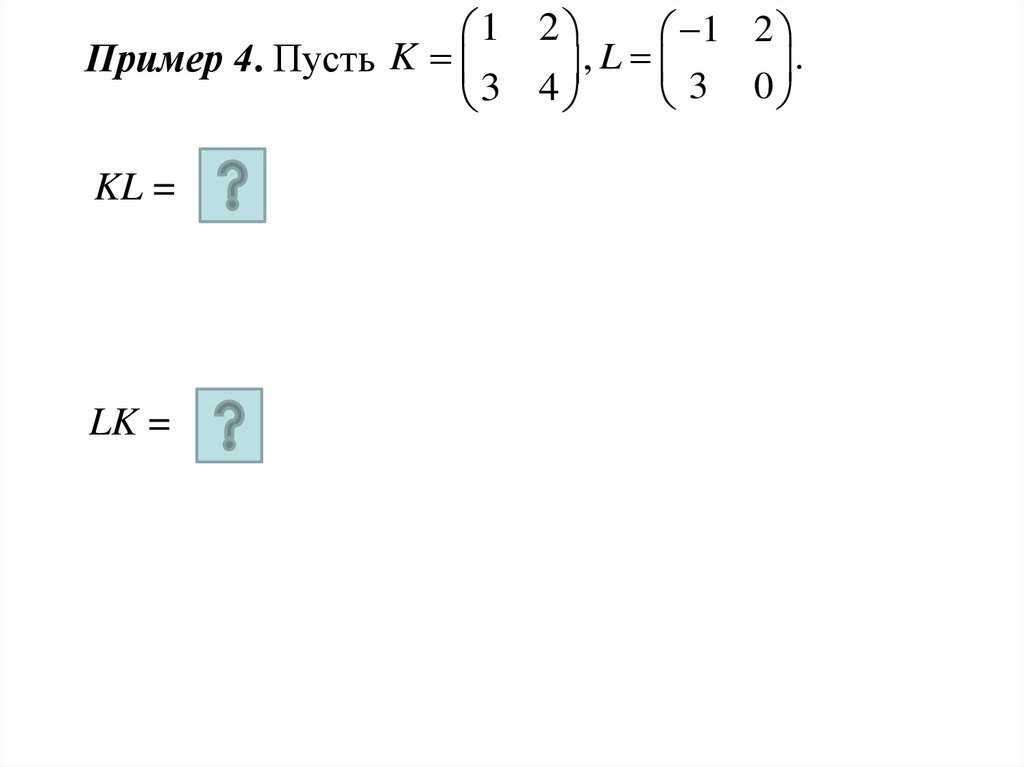








 mathematics
mathematics








