Лекция_15_формулы_10.12.2024

1. Лекция №15 Разработка программного обеспечения для моделирования физических процессов

Санкт-Петербургский политехнический университет Петра Великого
Лекция №15
Разработка программного обеспечения для
моделирования физических процессов
Воскобойников С.П.
Доцент ВШ ПИ ИКНК, к.ф.-м.н.
voskob_sp@spbstu.ru
10.12.2024

2. Содержание

• Метод сопряжённых градиентов (МСГ). НМСГ.
• Неполное разложение Холеского.
• Несимметричные системы
• Схемы хранения несимметричных и симметричных
разреженных матриц

3. Идея метода сопряжённых градиентов

Ax b,
x (0) ,
A AT ,
Ay, y 0,
s (i ) , i 1,2,..., n
x x
n
i s (i ) ,
i 1
n
As r ,
(i )
(0)
i
i 1
As , s 0,
(i )
i j,
( j)
r , s ,
As , s
i
x x
( 0)
(i )
(i )
(i )
n
(0)
i s (i ) ,
i 1
A x x( 0) r ( 0) ,
Ax Ax( 0) b Ax( 0) ,
( 0)
y 0

4. Идея метода сопряжённых градиентов

Ax b,
x
( n)
x,
x
(n)
x
A AT ,
Ay, y 0,
n
(0)
i s ,
(i )
x
i 1
(k )
x
r ( k ) r ( k 1) k As( k ) ,
x ,
k
(0)
i s (i ) ,
i 1
x ( k ) x ( k 1) k s ( k ) ,
(0)
y 0
s (1) ?,
r (0) b Ax(0) ,
k 1,2,..., n
r , s
As , s
( 0)
(k )
(k )
(k )
k
x ( k ) x ( k 1) k s ( k ) ,
r ( k ) r ( k 1) k As( k ) ,
s ( k 1) ?

5. Метод сопряжённых градиентов (явный)

Ax b,
A AT ,
Ay, y 0,
x (0) произвольное начальное приближение
s (1) r ( 0) ,
r (0) b Ax(0) ,
k 1,2,..., K max
r , r ,
As , s
k
( k 1)
( k 1)
(k )
(k )
x ( k ) x ( k 1) k s ( k ) ,
r ( k ) r ( k 1) k As ( k ) ,
r , r ,
r , r ,
r , r
(k )
k
(k )
(k )
(k )
( k 1)
( k 1)
s ( k 1) r ( k ) k s ( k ) ,
b,b ,
y 0

6. Двойственность метода сопряжённых градиентов

Ax b,
A AT ,
As , s 0,
i j,
r , r 0,
i j,
(i )
(i )
( j)
( j)
Ay, y 0,
r ( 0) , r (1) , ... , r ( n 1) , r ( n ) 0
J Az , z
(k )
(k )
z
(k ) 2
min
A k , k
y 0

7. Двухшаговость метода сопряжённых градиентов

x ( k ) x ( k 1) k s ( k ) ,
s ( k ) r ( k 1) k 1s ( k 1) ,
x ( k ) x ( k 1) k r ( k 1) k 1s ( k 1) ,
x ( k 1) x ( k 2) k 1s ( k 1) ,
s
x
(k )
( k 1)
x
( k 1)
x ( k ) x ( k 1)
k
x ( k 1) x ( k 2)
k 1
,
( k 1)
x( k 1) x( k 2)
,
k r
k 1
k 1
x ( k 1) x ( k 2)
k 1
Ax ( k 1) b,
k 1
k 1
k 1

8. Получение неявного метода сопряжённых градиентов

Ay, y 0,
Ax b,
A AT ,
B 1 Ax B 1b,
Cy d ,
1
2
u
d Cy ,
(1)
( 0)
d Cy
( 0)
,
1
2
y
(0)
( k 1)
ku ,
(k )
B y
( k ) ( k 1) k Cu ( k 1) ,
1
2
B
, ,
(k )
1
2
(k )
(k )
1
2
1
2 ( 0)
B y
1
2
B
( k 1)
1
2
1
2 (k )
1
2
1
2
1
2
B u
k B u ,
1
2
1
2
1
2
1
2
(k )
1
2
x
k B B AB u
(0)
B
1
2
b Ax B r ,
( 0)
1
2 ( 0)
B (0) ,
B r ,
( k 1)
С С T , С 0,
1
2
, ( k 1)
,
( k 1)
, u ( k 1)
( k 1)
k
u
(1)
1
2
B b B AB B x
r
y 0
d B b,
y B x,
(0)
Cu
y
1
2
( 0)
k 1,2,..., K max
(k )
1
2
C B AB ,
y ( 0) произвольное начальное приближение
( 0)
By , y 0,
B BT ,
y 0
( k 1)
,
(1)
r ,
( 0)
(k )
x
r
(k )
( k 1)
1
2
s
k s ,
B
(k )
(k )
(1)
s
1
2
B u (1) ,
(k )
1
2
B u (k )
r ( k ) r ( k 1) k As ( k 1) ,
(k )
d , d
, ,
,
k
(k )
(k )
( k 1)
( k 1)
u ( k 1) ( k ) k u ( k ) ,
1
2
B u
( k 1)
B B r
1
2
k B u (k ) ,
s ( k 1) B 1r ( k ) k s ( k ) ,
s ( k 1) w( k ) k s ( k ) ,
w( k ) B 1r ( k ) ,

9. Получение неявного метода сопряжённых градиентов

Cu
, ( k 1)
B 1r ( k 1) , r ( k 1)
w( k 1) , r ( k 1)
,
( k 1)
, u ( k 1)
As ( k 1) , s ( k 1)
As ( k 1) , s ( k 1)
12 12 12 ( k 1) 12 ( k 1)
B AB B s
,B s
( k 1)
k
12 ( k 1) 12 ( k 1)
B r
,B r
B r , r w , r ,
B r , r w , r
k
1 ( k )
(k )
(k )
(k )
1 ( k 1)
( k 1)
( k 1)
( k 1)
, B r , r w , r ,
d , d
g , b
B d , d
(k )
(k )
1 ( k )
(k )
1
Bg b
(k )
(k )
w( k ) B 1r ( k ) ,

10. Неявный метод сопряжённых градиентов

Ax b,
A AT ,
Ay, y 0,
y 0
B BT ,
By , y 0,
x (0) произвольное начальное приближение
r (0) b Ax(0) ,
Bw ( 0 ) r ( 0 )
s (1) w(0) ,
Bg b,
k 1,2,..., K max
w , r ,
As , s
k
( k 1)
( k 1)
(k )
(k )
x ( k ) x ( k 1) k s ( k ) ,
r ( k ) r ( k 1) k As ( k 1) ,
Bw ( k ) r ( k )
w , r ,
(k )
(k )
w , r ,
w , r
k
(k )
(k )
( k 1)
( k 1)
s ( k 1) w ( k ) k s ( k ) ,
g, b
y 0

11. О числе итераций в методе сопряжённых градиентов

Ax b,
A AT ,
Ay, y 0,
y 0
1
ln
n 1,
1
ln
q
r
( 0)
b Ax ,
( 0)
s
(1)
r ,
(0)
( 0)
(0)
( 0)
1
By , y 0,
y 0
1
1
2 B 1 A
1
1
q
r , r ,
Ar , r
( 0)
B BT ,
,
2 B 1 A
x (1) x ( 0) 1r ( 0) ,
r (1) r ( 0) 1 Ar ( 0) ,
A
r (0)
b Ax( 0)
x ( 0 ) A 1b A 1 x
1
r , r , , 1
Ar , r A , ,
1
r (1) r ( 0) 1 Ar ( 0)
1
A
1
( 0)
( 0)
( 0)
( 0)
0,
x (1) x ( 0 ) 1r ( 0 ) x ( 0)
1
x
1
1
x,

12. О выборе матрицы предобусловливания

Ax b,
A AT ,
Ay, y 0,
y 0
a11
a22
D
...
B D
~L
~T
B L
B BT ,
ann
~
lij 0, i j
Bw ( 0 ) r ( 0 )
L~y0 r0 ,
Bw ( k ) r ( k )
~y r ,
L
k
k
L~T w0 y0 ,
~T w y ,
L
k
k
By , y 0,
y 0

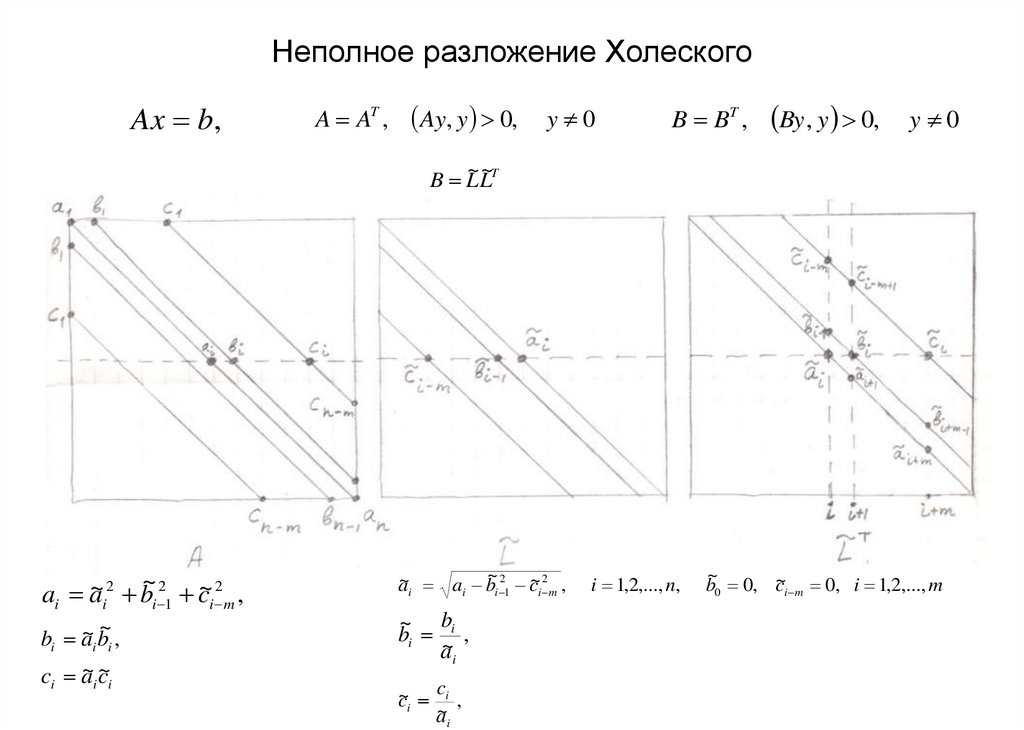
13. Неполное разложение Холеского

Ax b,
A AT ,
Ay, y 0,
y 0
B BT ,
By , y 0,
y 0
~L
~T
B L
~
ai a~i2 bi 21 c~i 2 m ,
~
bi a~i bi ,
c a~ c~
i
i i
~
a~i ai bi 21 c~i 2 m ,
~ b
bi i ,
a~i
c
c~i i ,
a~i
i 1,2,..., n,
~
b0 0, c~i m 0, i 1,2,..., m

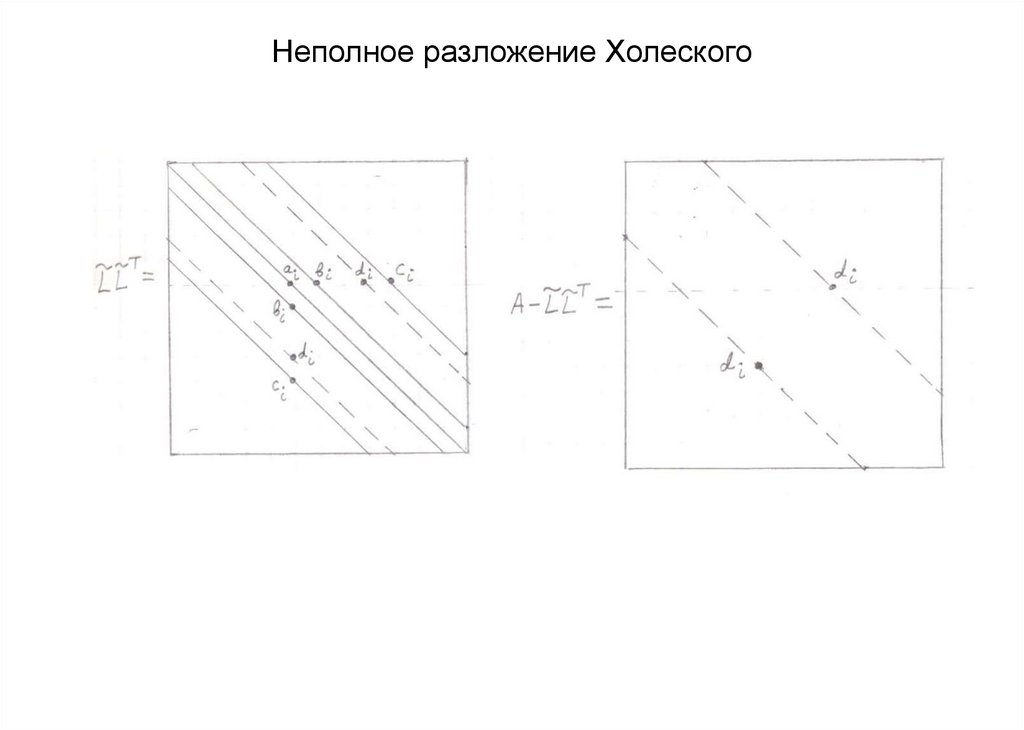
14. Неполное разложение Холеского

15. Несимметричные системы

Ax b,
C AT A,
AT Ax AT b,
d AT b,
x (0) произвольное начальное приближение
d, d
A AT
Cx d
С СT ,
C 2 A
С 0,
x (0) произвольное начальное приближение
d, d
r ( 0) d Cx( 0) ,
r ( 0) AT b Ax ( 0) ,
s (1) r ( 0) ,
s (1) r ( 0) ,
k 1,2,..., K max
k 1,2,..., K max
r
Cs
( k 1)
k
, r ( k 1)
,
( k 1)
( k 1)
,s
y ( k 1) As ( k 1)
k
r
y
( k 1)
, r ( k 1)
,
( k 1)
, y ( k 1)
x ( k ) x ( k 1) k s ( k ) ,
x ( k ) x ( k 1) k s ( k ) ,
r ( k ) r ( k 1) k Cs ( k 1) ,
r ( k ) r ( k 1) k AT y ( k 1) ,
r , r ,
r , r ,
r , r ,
r , r
r , r ,
r , r
(k )
k
(k )
(k )
(k )
( k 1)
( k 1)
s ( k 1) r ( k ) k s ( k ) ,
(k )
k
(k )
(k )
(k )
( k 1)
( k 1)
s ( k 1) r ( k ) k s ( k ) ,

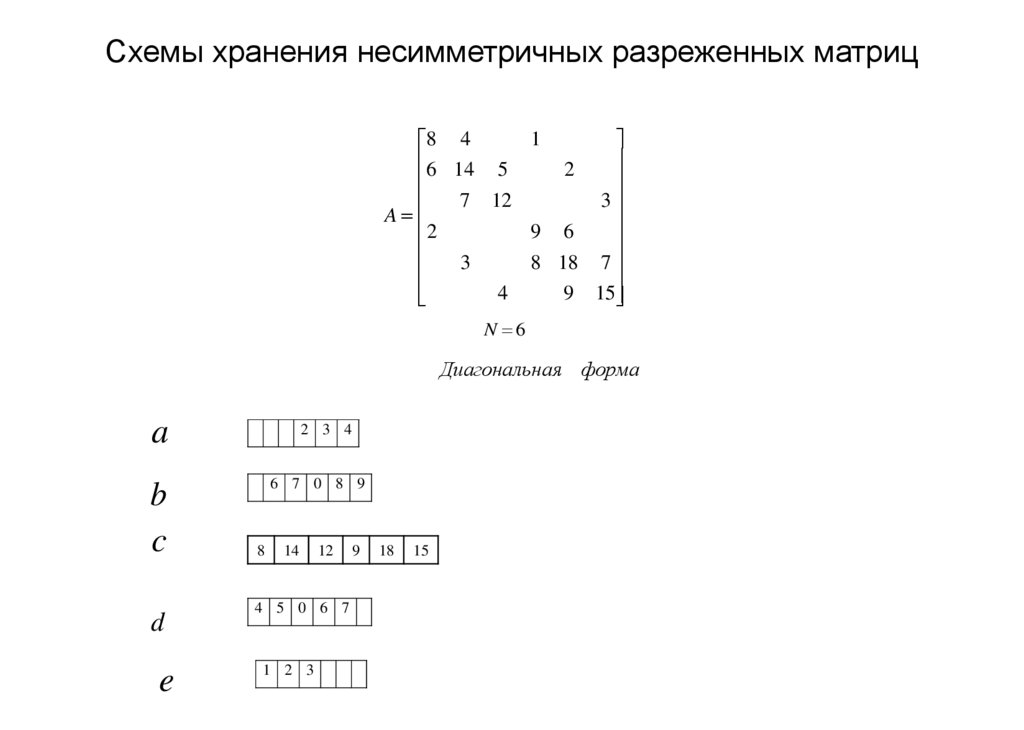
16. Схемы хранения несимметричных разреженных матриц

1
8 4
6 14 5
2
7 12
3
A
2
9
6
3
8 18 7
4
9 15
N 6
Диагональн ая форма
a
2 3 4
b
c
6 7 0 8 9
d
e
8
14
12
4 5 0 6 7
1 2 3
9
18
15

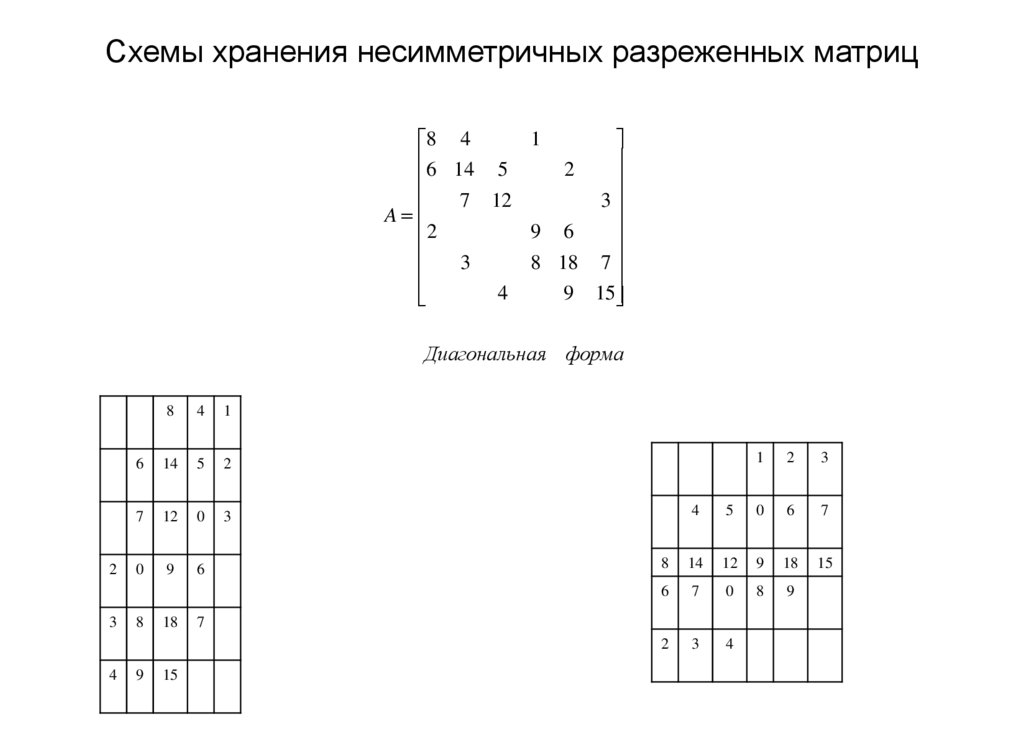
17. Схемы хранения несимметричных разреженных матриц

1
8 4
6 14 5
2
7 12
3
A
2
9
6
3
8 18 7
4
9 15
Диагональн ая форма
2
3
4
8
4
1
6
14
5
2
7
12
0
3
0
9
6
8
9
18
15
1
2
3
4
5
0
6
7
8
14
12
9
18
15
6
7
0
8
9
2
3
4
7

18. Схемы хранения несимметричных разреженных матриц

1
8 4
6 14 5
2
7 12
3
A
2
9
6
3
8 18 7
4
9
15
N z 20
Координатный
A 15 4
IR 6 1
IC 6 2
2
2
5
5
2
3
3
5
2
4
6
3
6
2
1
7
3
2
8
5
4
9
6
5
8
1
1
1
1
4
14 12 3
2 3 3
2 3 6
2
4
1
6
4
5
18
5
5
9 7
4 5
4 6
18
5
5
7 4
5 6
6 3
9
6
5
15
6
6
18
5
5
9 3 7 15
6 3 5 6
5 6 6 6
Координатный по строкам
A
IR
IC
8
1
1
4
1
2
1
1
4
6
2
1
14
2
2
5
2
3
2
2
5
7
3
2
12
3
3
3
3
6
2
4
1
9
4
4
6
4
5
3
5
2
8
5
4
Координатный по столбцам
A
IR
IC
8 6
1 2
1 1
2
4
1
4
1
2
14
2
2
7 3 5
3 5 2
2 2 3
12
3
3
4 1 9
6 1 4
3 4 4
8
5
4
2
2
5
6
4
5

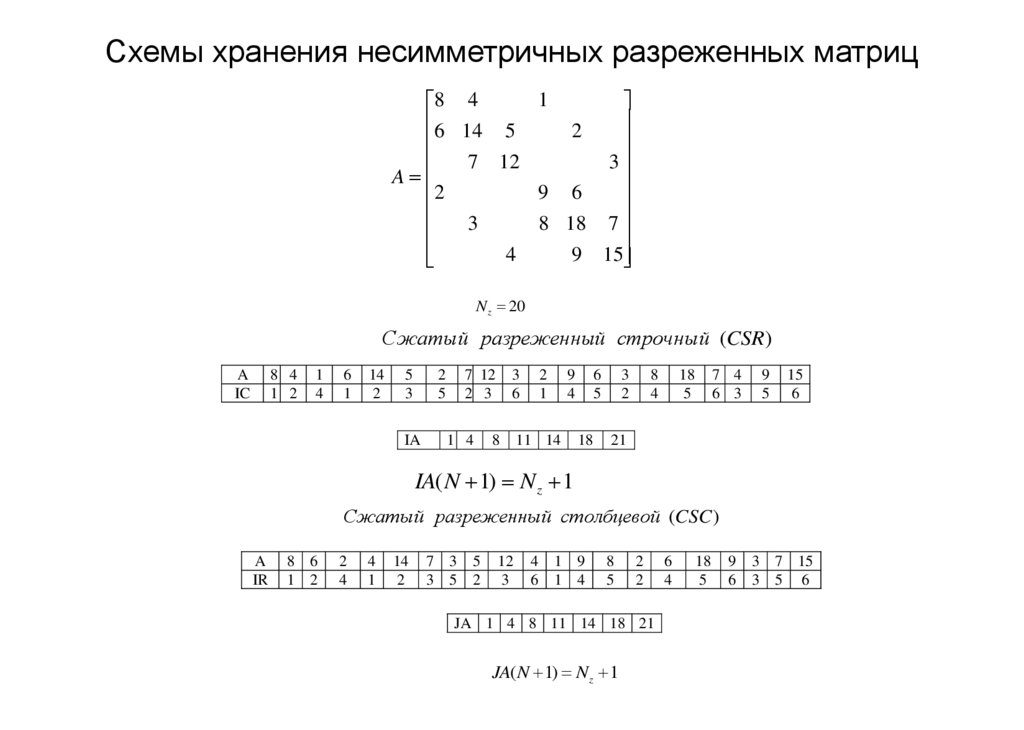
19. Схемы хранения несимметричных разреженных матриц

1
8 4
6 14 5
2
7 12
3
A
2
9
6
3
8 18 7
4
9
15
N z 20
Сжатый разреженный строчный (CSR)
A
IC
8 4
1 2
1
4
6
1
14
2
5
3
2
5
IA
7 12
2 3
1 4
3
6
8
2
1
9
4
11 14
6
5
18
3
2
8
4
18
5
7 4
6 3
9
5
15
6
21
IA( N 1) N z 1
Сжатый разреженный столбцевой (CSC )
A
IR
8 6
1 2
2
4
4
1
14
2
7 3 5
3 5 2
12
3
4 1 9
6 1 4
8
5
2
2
JA 1 4 8 11 14 18 21
JA( N 1) N z 1
6
4
18
5
9 3 7 15
6 3 5 6

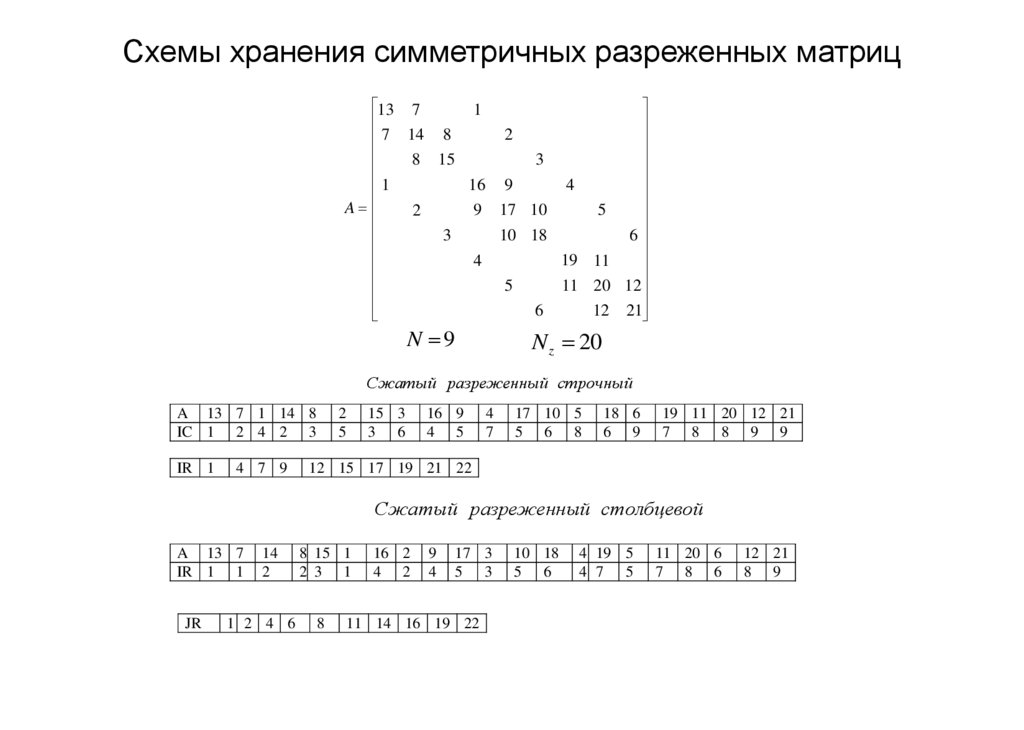
20. Схемы хранения симметричных разреженных матриц

13 7
1
2
7 14 8
8 15
3
16 9
4
1
A
9 17 10
5
2
3
10 18
6
19 11
4
5
11 20 12
6
12 21
N 9
N z 20
a 13 14 15 16 17 18 19 20 21
b 7 8 0 9 10 0 11 12 0
c 1 2 3 4 5 6 0 0 0
13 7 1
14 8 2
15 0 3
16 9 4
B 17 10 5
18 0 6
19 11 0
20 12 0
21 0 0
1 2 3 4 5 6
B
7 8 0 9 10 0 11 12
13 14 15 16 17 18 19 20 21

21. Схемы хранения симметричных разреженных матриц

13 7
1
2
7 14 8
8 15
3
16 9
4
1
A
9 17 10
5
2
3
10 18
6
19
4
11
5
11 20 12
6
12 21
N 9
N z 20
Сжатый разреженный строчный
A 13 7 1 14 8
IC 1 2 4 2 3
IR 1
4 7 9
2
5
15 3
3 6
16 9
4 5
4
7
17 10 5
5 6 8
18 6
6 9
19 11 20 12 21
7 8 8 9 9
12 15 17 19 21 22
Сжатый разреженный столбцевой
A 13 7
IR 1 1
JR
14
2
8 15 1
2 3 1
1 2 4 6
8
16 2
4 2
9
4
17 3
5 3
11 14 16 19 22
10 18
5 6
4 19 5
4 7 5
11 20 6
7 8 6
12 21
8 9