Симплекс - метод. Линейное программирование. Каноническая форма

1.

Лекция
Симплекс-метод
Домашова Д.В.
1

2.

Идея симплекс-метода решения задачи ЛП
Свойства задачи линейного программирования наталкивают на следующую
схему решения задачи линейного программирования, известную, как симплексметод.
Пусть рассматриваемая задача имеет непустое допустимое множество с
вершинами.
Тогда:
Тем или иным способом находим какую-нибудь вершину допустимого
множества и по определенным критериям определяем, не является ли она
оптимальной.
Если она оптимальна, то задача решена. Если нет, то
используя определенные правила, проверяем, нельзя ли утверждать, что
задача не имеет оптимального решения (целевая функция не ограничена
сверху или, соответственно, снизу на допустимом множестве).
Если утверждать это можно, то задача неразрешима. Если нельзя, то
по определенному правилу ищем новую, лучшую (в смысле значения целевой
функции) вершину и переходим к пункту 1).
2

3.

Идея симплекс-метода решения задачи ЛП
Для реализации предложенной схемы необходимо:
указать способ нахождения вершины допустимого множества,
критерии оптимальности, неразрешимости,
способ перехода от одной вершины к другой, лучшей в смысле
значения целевой функции.
3

4.

Линейное программирование
Каноническая форма
Задачу линейного программирования представленную в виде:
f c1 x1 c2 x2 ... cn xn max(min)
a11x1 + a12x2 + … + a1nxn = b1
a21x1 + a22x2 + … + a2nxn = b2
… … … … … …
am1x1 + am2x2 + … + amnxn = bm
x 0 , i 1,n
(3)
i
будем называть канонической задачей линейного программирования.

5.

Линейное программирование
Приведение к канонической форме
Введем две дополнительные неотрицательные переменные x4 и x5 в
первом и третьем ограничениях, так, чтобы получились ограничениянеравенства.
Переменную x3 представим в виде: x3 x3' x3'' , где x3’ 0, x3’’ 0.
Получим: F x 1 2x 1 x 3' x 3'' max
x1 + 2x2 + 3x3 + x4 = 5
2x1 + 3x2 – 4(x3’ – 3x3’’) = 3
- x1 + x2 – (x3’– x3’’) – x5 = 2
x1 0 , x2 0, x3’ 0, x3’’ 0, x4 0, x5 0 ,
Получили задачу в канонической форме.

6.

Линейное программирование
Задача ЛП в векторном виде
Введем в рассмотрение:
x1
b1
C ( c1 , c 2 ,..., cn ) , X , b
xn
bn
a 11 a 1n
a 21 a 2n
A
a m1 a mn
Перепишем задачу (3) линейного программирования
в векторной форме:
F c x max
A x b
x 0

7.

Линейное программирование
f c x c x ... c x max
1
1
2
2
n
n
a11x1 +…+ a1nxn = b1
… … … …
am1x1 +…+ amnxn = bm
x1 0, … , xm 0
Введем в рассмотрение векторы
a 1j
a 2j
Aj ,
a
mj
j 1,n
f (c, x) max
A x A x ... A x b
1
x 0
1
2
2
n
n
Задачу ЛП можно трактовать
следующим образом: из всех
разложений вектора b по
векторам A1…An с
неотрицательными
коэффициентами требуется
выбрать хотя бы одно такое,
коэффициенты xj, j=1,n,
которого доставляют целевой
функции f оптимальное
значение.
Не ограничивая общности,
считаем ранг матрицы A
равным m и n>m (случай n=m –
тривиален).
7

8.

Опорные точки допустимого множества
Определение. Ненулевое допустимое решение
x ( x1 ,..., xn )
называется опорным, если векторы Aj , соответствующие отличным от
нуля координатам вектора x, линейно - независимы.
Определение. Ненулевое опорное решение назовем невырожденным,
если оно имеет точно m положительных координат.
Определение. Если число положительных координат
решения меньше m, то оно называется вырожденным.
опорного
Определение. Упорядоченный набор из m линейно-независимых
векторов Aj, соответствующих положительным координатам опорного
решения назовем базисом.
8

9.

Опорные точки допустимого множества
Пример. Дана система ограничений задачи:
2x1 + x2 +3x3 = 2
x1 – 2x3 + x4 = 1
x1 0 , x2 0, x3 0 , x4 0
Здесь m=2;
2
1
3
0
,
,
,
A1 1 A2 0 A3 2 A4 1
Классифицировать точки:
x
(1)
(0,2,0,1),
x
(2)
(1,0,0,0),
x
(3)
( 1 ,1,0, 1 )
2
2
9

10.

Опорные точки допустимого множества
Теорема о связи опорного решения и вершины
допустимого множества
Теорема.
Вектор x ( x1 ,..., xn ) тогда и только тогда является опорным решением
задачи, когда точка
множества.
x ( x ,..., x )
1
n
является вершиной допустимого
Таким образом, задача нахождения вершины допустимого множества
свелась к задаче нахождения опорного решения, а, следовательно, к
нахождению базиса.
Будем считать, что исходный базис A1, A2, … , Am дан.
Отправляясь от него, покажем, как найти опорное решение.
Сформулируем условие оптимальности решения, условие отсутствия
решения.
Покажем, как перейти к базису, дающему лучшее решение.
10

11.

Симплекс-метод
f c, x max
Ax b
x 0
rg A m
A1 ,..., Am - базис,
AB A1...Am , As Am 1...An
A AB , As
x x B , xs , c c B , cs
11

12.

Симплекс-метод
Ax b
AB x B As x s b
1
1
x B AB As x s AB b
x B AB 1 b As xs
x A b A x , 0 A b,0
0
1
B
s s
1
B
12

13.

Симплекс-метод
f x c B x B cs xs
13

14.

Симплекс-метод
f x c B x B cs xs
cB AB 1b AB 1 As xs cs xs
14

15.

Симплекс-метод
f x c B x B c s x s
1
B
1
B
c B A b A As x s c s x s
c B AB 1b c s c B AB 1 As x s
15

16.

Симплекс-метод
f x c B x B c s x s
1
B
1
B
c B A b A As x s c s x s
c B AB 1b c s c B AB 1 As x s
f x on c B AB 1b ,
т.к. x s 0
f x f x on cs c B AB 1 As xs
s cs c B AB 1 As ,
s m 1, n
x f x x
f x f x
on
on
s s
n
j m 1
j
j
16

17.

Симплекс-метод
Идея симплекс-метода состоит в том,
чтобы исходя из начального опорного
решения найти новое опорное
решение, исключая для этого
некоторый вектор
из начального базиса и заменяя его
одним из небазисных векторов
таким образом,
чтобы новое опорное решение не
ухудшало значения целевой функции.
17

18.

Симплекс-метод
Выводы:
1) небазисный Ar имеет смысл вводить в новый базис, если r 0 ;
2) причем лучше всего такой Ar , у которого r 0 и самая большая из
r m 1, n ;
3) если все j 0, j 1, n , то значение целевой функции улучшить
всех
нельзя, следовательно, рассматриваемое опорное решение является
оптимальным.
18

19.

Симплекс-метод
Определим, какой вектор должен быть исключен из базиса.
Так как АB – базис в Rm все столбцы матрицы А и b можно
представить в виде линейных комбинаций данных столбцов
x10
m
b A j x j 0 A1 ,...Am ... AB x 0
j 1
x
m0
x1k
m
Ak A j x jk A1 ,..., Am ... AB x k
j 1
x
mk
19

20.

Симплекс-метод
x10
b A j x j 0 A1 ,...Am ... AB x 0
j 1
x
m0
m
x1k
Ak A j x jk A1 ,..., Am ... AB x k
j 1
x
mk
m
x 0 AB 1b ненулевые координаты опорной точки
k
1
x AB Ak , k 1, n координаты разложения вектора Ak по базису
k ck cB AB 1 Ak ck cB x k ck
m
c j m x jk
j 1
20

21.

Симплекс-метод
AB 1b ненулевые координаты опорной точки
AB 1 Ar координаты разложения вектора А r по базису
21

22.

Симплекс-метод
правило выбора вектора, выводимого из базиса
22

23.

Симплекс-метод
правило выбора вектора, выводимого из базиса
Выводится тот вектор As, для которого отношение
координат опорного решения к положительным
координатам разложения вектора Ar по базису
является минимальным
xs 0
xi 0
min
i I xir
xsr
23

24.

Симплекс-метод
Критерий отсутствия решения
Существует r 0 , такая, что если все xir 0, i 1, m , то
задача не имеет решения, т.е. существуют допустимые
решения со сколь угодно большим значением целевой
функции.
В этих случаях говорят, что целевая функция не ограничена
сверху в допустимой области
24

25.

Алгоритм Симплекс-метода
1. Для известного начального базиса находят
разложения векторов b и Ak k 1, n по базису:
координаты
0
1
x AB b ненулевые координаты опорной точки
k
1
x
A
Ak , k 1, n координаты разложения вектора Ak по базису
B
2. Вычисляют симплекс-разности:
k ck c B AB 1 Ak , k 1, n
3. Проверяют план на оптимальность:
Если все k 0, k 1, n,
то решение оптимально.
4. Проверяется критерий отсутствия решения:
Если r 0: все xir 0, i 1, m , то целевая функция не ограничена
сверху в допустимой области.
5. Определяют вектор Ar, вводимый в базис: r 0 и максимальная
среди всех положительных k , k 1, n
6. Определяют вектор As, выводимый из базиса.
As :
xs 0
x
min i 0
i I xir
xsr
xir 0 строим новый базис и переходим в п.1
25

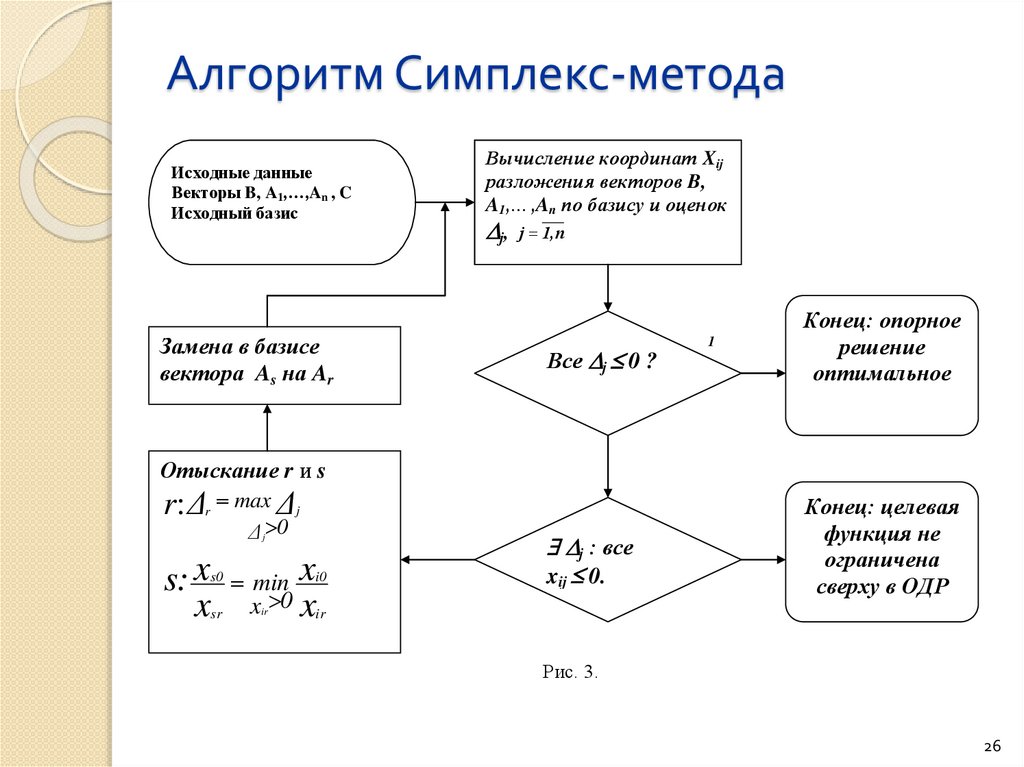
26.

Алгоритм Симплекс-метода
Исходные данные
Векторы B, A1,…,An , C
Исходный базис
Замена в базисе
вектора As на Ar
Вычисление координат Xij
разложения векторов B,
A1,…,An по базису и оценок
j, j 1,n
Все j 0 ?
1
Конец: опорное
решение
оптимальное
Отыскание r и s
r: Δ max Δ
r
Δ j 0
j
x
s: x min
x x 0 x
s0
sr
i0
ir
j : все
xij 0.
Конец: целевая
функция не
ограничена
сверху в ОДР
ir
Рис. 3.
26

27.

Симплекс-метод
Формулы пересчета координат разложения векторов по
новому базису
x jr
x sk , если j I \ s
x jk
xsr
x jk
xsk , если j r
xsr
27

28.

Симплекс-метод
Формулы пересчета координат разложения векторов по
новому базису
Доказательство
1) Вектор Ak через старый базис:
Ak A j x jk , k 1, n
j I
2) Вектор Ak через новый базис:
, k 1, n
Ak A j x jk Ar xrk
j I \ s
Вектор
Ar A j x jr A j x jr As xsr
j I
j I \ s
x jr
Ar
As
Aj
, т.к. xsr 0
xsr j I \ s xsr
28

29.

Симплекс-метод
Формулы пересчета координат разложения векторов по
новому базису
Доказательство
3) Подставим As в (1) и получим
Ak Aj x jk As xsk
j I \ s
xsk
x jr xsk
Aj x jk Ar
Aj
x
x
j I \ s
j
I
\
s
sr
sr
x jr xsk
x
Ar sk
Aj x jk
xsr
xsr
j I \ s
29

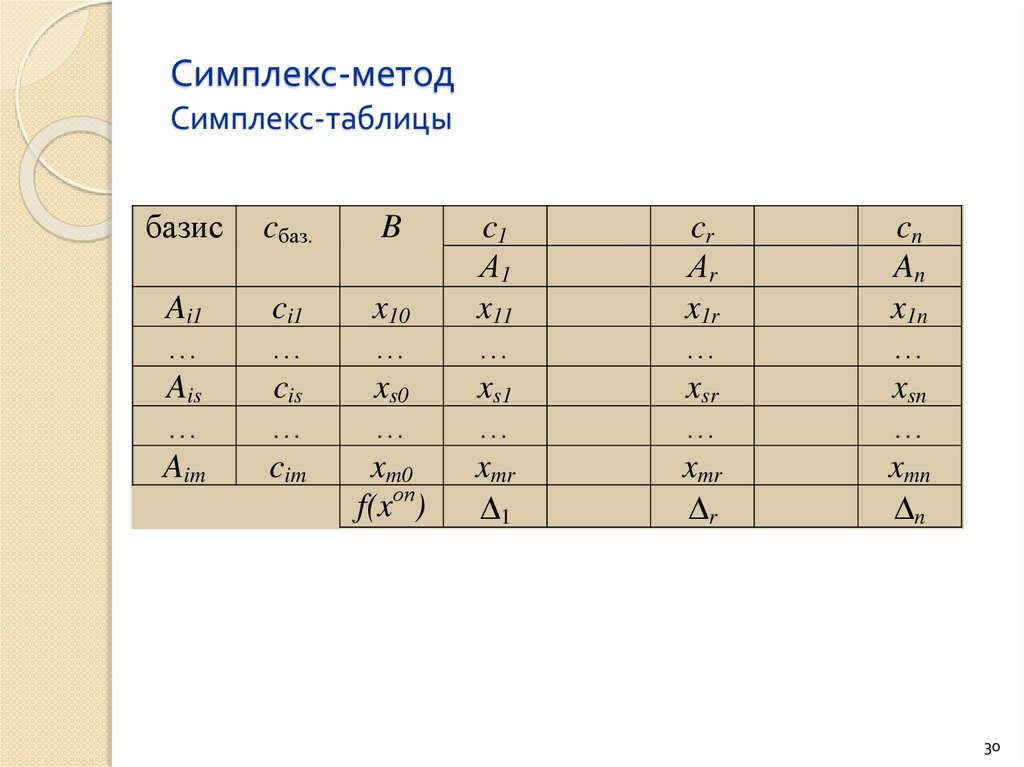
30.

Симплекс-метод
Симплекс-таблицы
базис
cбаз.
B
Ai1
…
Ais
…
Aim
ci1
…
cis
…
cim
x10
…
xs0
…
xm0
f(xоп)
c1
А1
x11
…
xs1
…
xmr
1
cr
Аr
x1r
…
xsr
…
xmr
r
cn
An
x1n
…
xsn
…
xmn
n
30

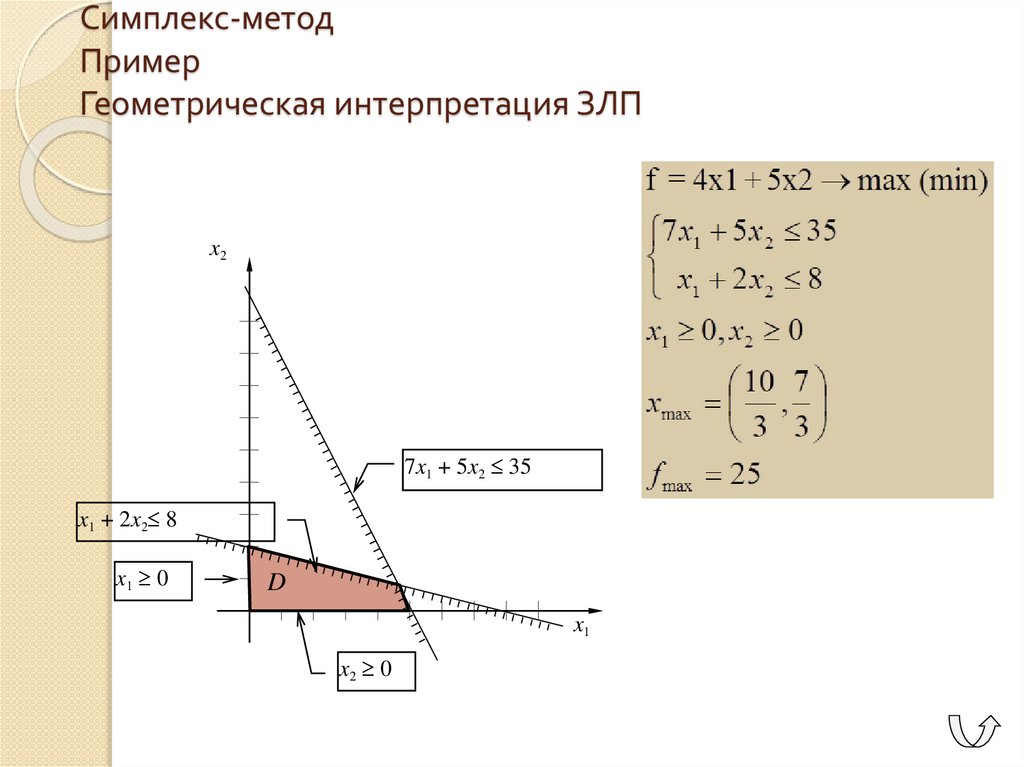
31.

Симплекс-метод
Пример
Геометрическая интерпретация ЗЛП
x2
7x1 + 5x2 35
x1 + 2x2 8
x1 0
D
x1
x2 0

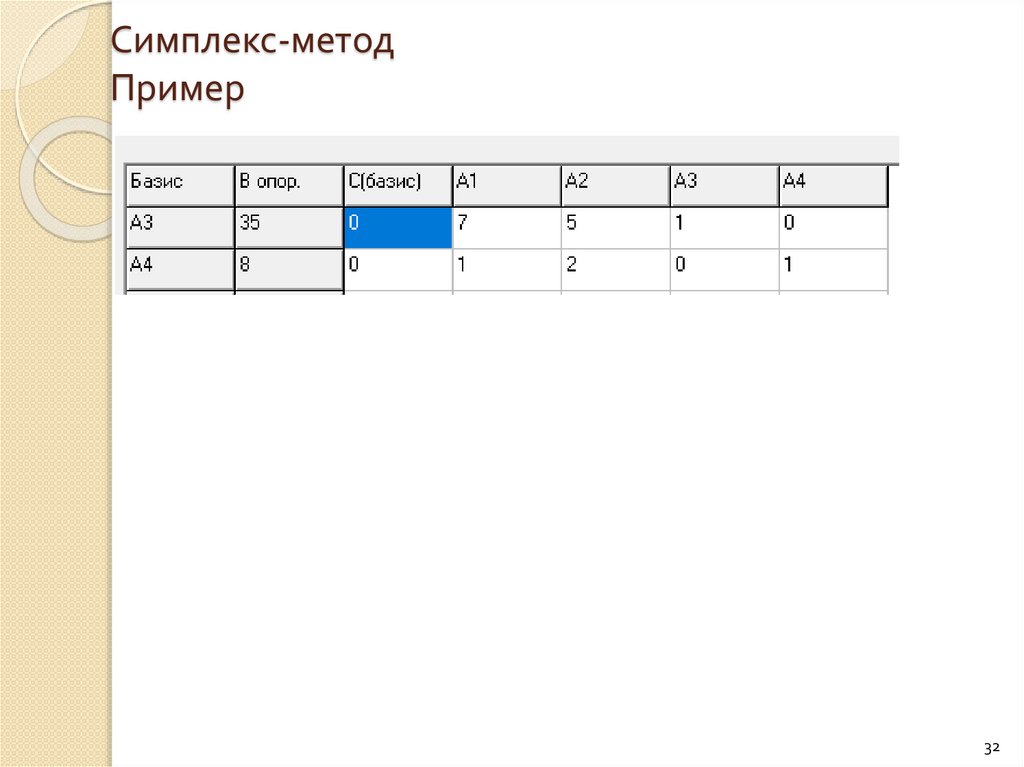
32.

Симплекс-метод
Пример
32

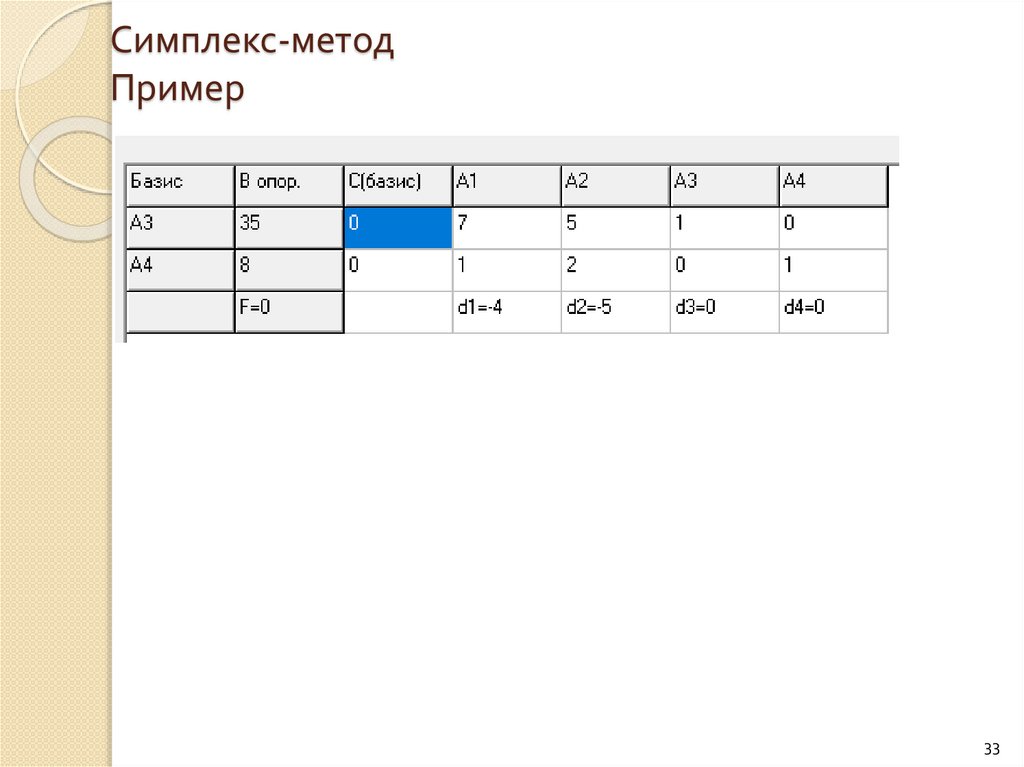
33.

Симплекс-метод
Пример
33

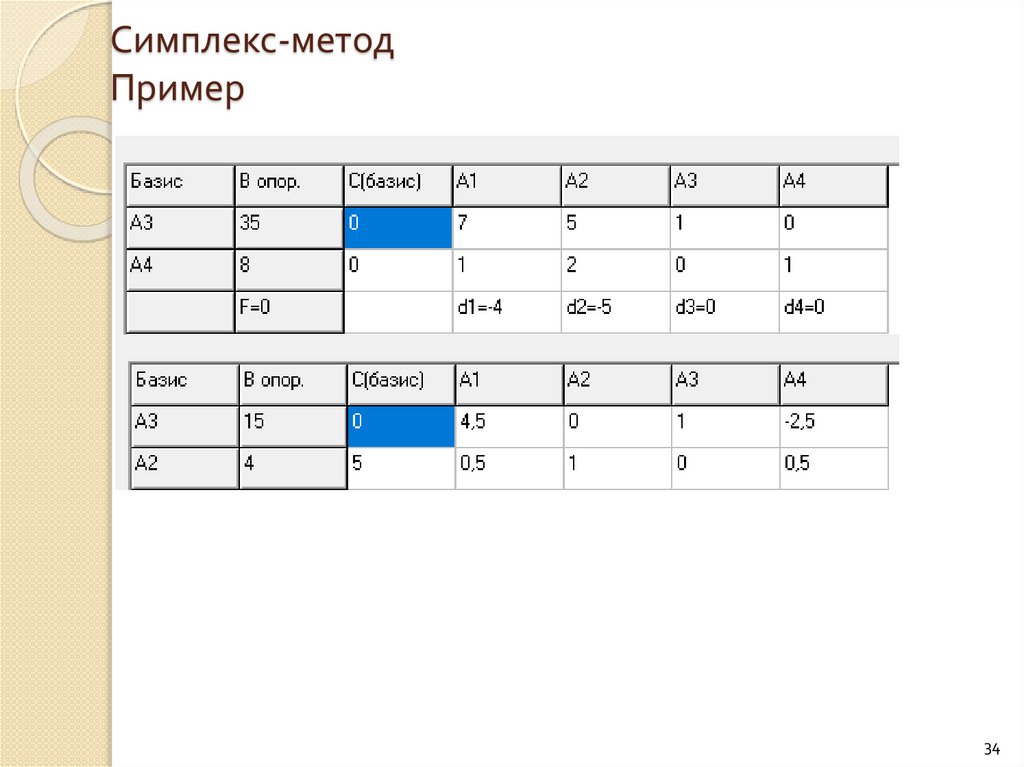
34.

Симплекс-метод
Пример
34

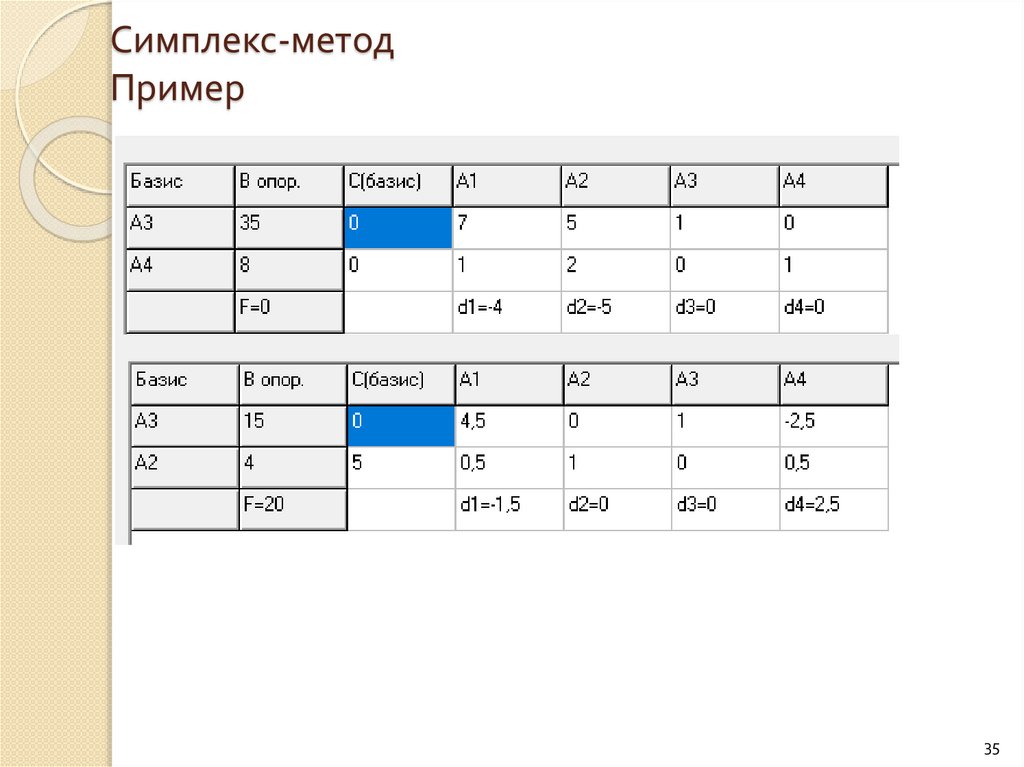
35.

Симплекс-метод
Пример
35

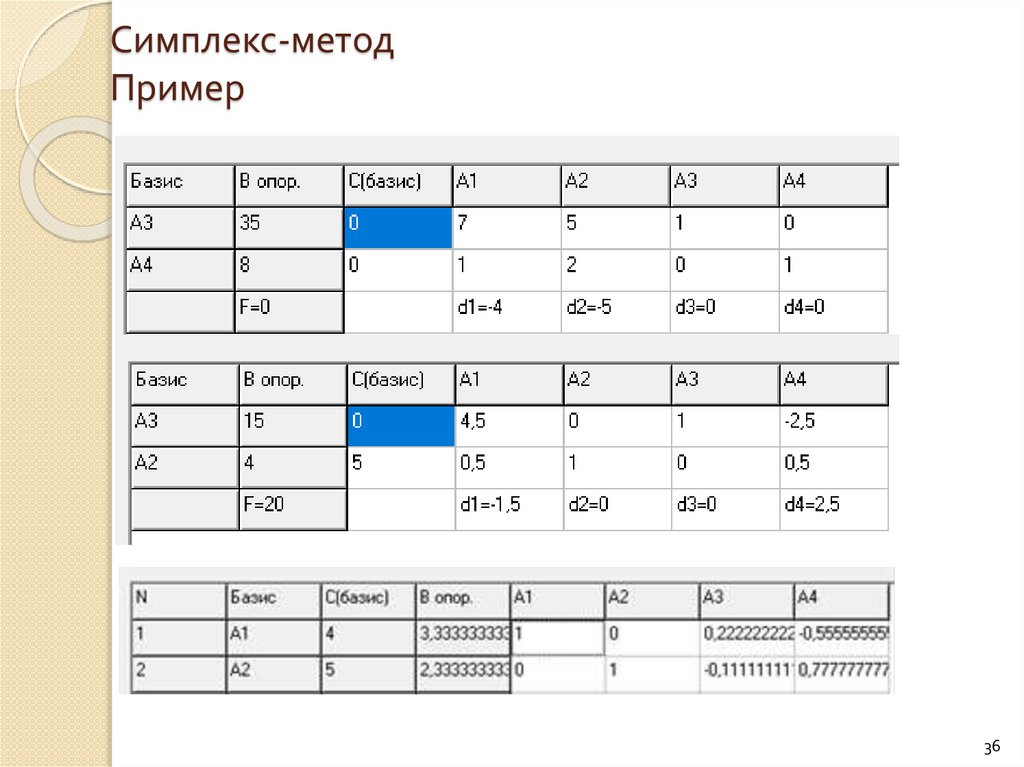
36.

Симплекс-метод
Пример
36

37.

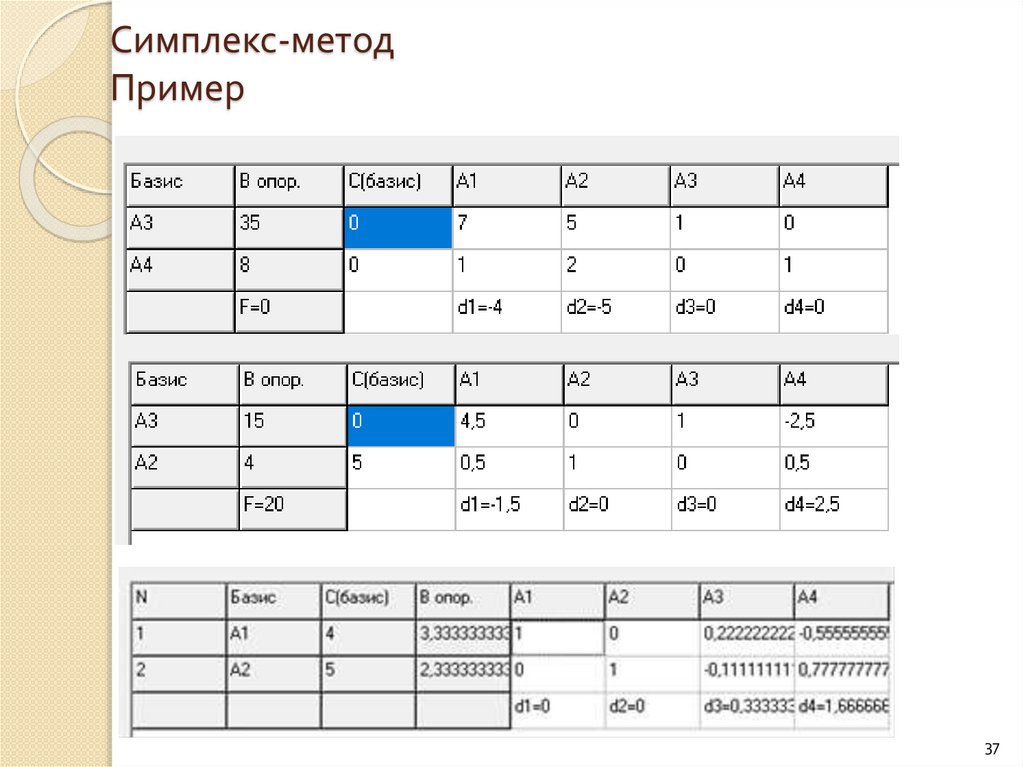
Симплекс-метод
Пример
37

38.

Симплекс-метод
Пример
38

39.

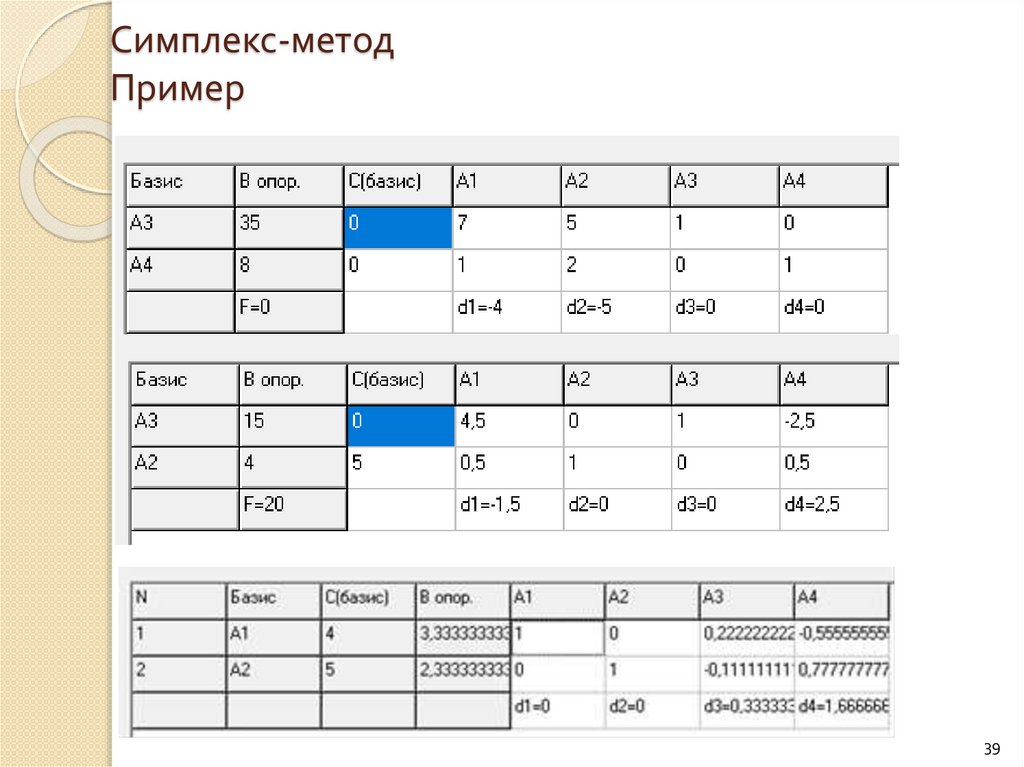
Симплекс-метод
Пример
39

40.

Симплекс-метод
Вообще говоря, поиск опорной точки множества D по своей
трудоемкости
сопоставим
с самой
процедурой
симплекс-метода.
Поиск
начальной
опорной
точки
методом
искусственного базиса
Будем считать, что для задачи (1)
c, x max
D : Ax b, x 0
(1)
выполнено условие b 0
Рассмотрим вспомогательную задачу:
m
yi max (2)
i 1
~
D : Ax y b, x 0, y 0
n
m
~
D x, y Rn m : A j x j ei yi b, x 0, y 0
j 1
i 1
0, b - опорная точка в D .
Целевая функция вспомогательной задачи ограничена сверху
нулем (0). Следовательно, эта задача имеет оптимальное решение.
40

41.

Симплекс-метод
Поиск начальной опорной точки методом искусственного базиса
G y y ... y max
a x ... a x y b
a x ... a x 0 y y b
1
2
m
11
1
1n
n
21
1
2n
n
1
1
2
... a mn x n 0 y ... y bm
1
m
a m1 x 1
1
2
x 0, j 1,n
j
y 0, i 1,m
i
Переменные y1, y2, … , ym – называют искусственными
переменными.
1
0
Очевидно, что векторы An 1 0 ,
0
0
0
1
0
An 2 0 , ... , An m 0
0
1
образуют базис для опорного решения x ( 0 ,0 ,...,0 ,b1 ,b2 ,...,bm ) ,
n
который называют искусственным базисом.
41

42.

Симплекс-метод
Поиск начальной опорной точки методом искусственного базиса
Утверждение.
m
Пусть (x ,y ) – решение задачи (2) и f yi*
*
*
*
i 1
Если f*=0, то x* - опорная точка множества D.
Если f*<0, то задача (1) не имеет допустимых точек: множество D пусто.
Доказательство:
~
1) Если f*=0, y*=0, то (x*,0) – опорная точка множества D и D,
следовательно, оптимальный базис вспомогательной задачи можно
взять в качестве начального для задачи (1).
~
2) Если f <0, то, если x D x,0 D , что несовместимо с
*
условием f*<0 задача (1) не имеет область допустимых решений.
42

43.

Симплекс-метод
Поиск начальной опорной точки методом искусственного базиса
Решая вспомогательную задачу симплекс-методом,
(0)
(0)
(0)
оптимальное решение x(0) ( x(0)
,...,
,
,...,
x n y1 y m ) .
1
мы
найдем
Если в этом решении среди искусственных переменных есть
положительные, то исходная задача линейного программирования
неразрешима, так ее ОДР пуста.
Если же
(0)
y 0, i 1,m ,
i
то базис, соответствующий оптимальному
решению вспомогательной задачи, можно взять в качестве исходного
базиса основной задачи.
43

44.

Поиск начальной опорной точки методом искусственного базиса
Пример
F 5 x1 2 x2 max(min)
5 x1 6 x2 30
x1 2 x2 4
x1 0 x2 0
5 x1 6 x 2 30
x1 2 x 2 4
n grad F (5,2)
x1 2 x2 4
x1 0
x 0; 2
F 4
xmin (0, 2)
F ( xmin ) 4
44

45.

Поиск начальной опорной точки методом искусственного базиса
Пример
F 5 x1 2 x2 max(min)
5 x1 6 x2 x3 30
x1 2 x2 x4 4
x1 0 x2 0 x3 0 x4 0
G y1 max(min)
5 x1 6 x2 x3 30
x1 2 x2 x4 y1 4
x1 0 x2 0 x3 0 x4 0 y1 0
Базис Сбаз
B (опорное
0
0
0
решение)
A1
A2
A3
0
A4
-1
A5
A3
0
30
5
-6
1
0
0
A5
-1
4
1
2
0
-1
1
Оценки
F=0
1 1
2 2
3 0
4 1
5 0
45

46.

Замечания
Проблема зацикливания.
◦ Вырожденные планы могут привести к зацикливанию, т.е. к
многократному повторению процесса вычислений, не
позволяющему получить оптимальный план.
◦ Можно использовать метод Крено: Элементы строк, имеющие
одинаковые наименьшие симплексные отклонения, делятся на
предполагаемые разрешающие элементы. За ведущую
выбирается та сторона, в которой раньше встретится
наименьшее частное при просмотре слева направо по
столбцам.
Бесчисленное множество решений
◦ Если в строке ∆ оптимального плана находится нуль,
принадлежащий свободной переменной, вектор которой не
входит в базис, а в столбце этого вектора имеется хотя бы один
положительный элемент, то задача имеет бесчисленное
множество решений.
◦ Свободные переменные можно ввести в базис, в результате
будет получен новый оптимальный план с другим набором
базисных переменных.
46

47.

Проверяли: Абаева Зарина и Бакшеева Татьяна (С18-702)
Список опечаток :
№
слайда
Ошибка
Исправление
5
Опечатка в целевой функции