Лекция 1 сгм 25-26

1.

Специальные главы математики
Лекция 1
Числовые ряды
Поторочина К.С.
Доцент ДИТиА, ИРИТ-РТФ

2.

О дисциплине
Курс в LMS Moodle:
Специальные главы математики ИРИТ-РТФ 25-26 (Поторочина КС)
• Код доступа: сгм25
• Команда в Телеграм

3.

О дисциплине
Разделы:
• Ряды (числовые и функциональные).
КР Числовые ряды. + ИДЗ Функциональные ряды.
• ТФКП.
КР Вычисление ФКП. Дифференцируемость и аналитичность ФКП.
+ КР Интегрирование ФКП
• Операционное исчисление.
КР Изображение и оригинал функции. Решение ДУ операционным
методом.

4.

Литература
1. Краснов М.Л. Киселев А.И., Макаренко Г.И.
Вся высшая математика: Учебник. Т. 3, 4. 2001
2. Функции комплексного переменного. Задачи и примеры с подробными
решениями/ Краснов М.И., Киселев А.И., Макаренко Г.И., 2003
3. Сборник задач по математике для втузов. Ч.3/ Ефимов А.В., Поспелов
А.С., 2003
4. Табуева В.А. Математика. Математический анализ. Специальные
разделы: Уч.пособие. Ек-г, 2004
4

5.

Тема 1. Ряды
1. Числовые ряды: основные понятия
Рассмотрим числовую последовательность
а1, а2,…, аn,…={an}, где an − действительные или комплексные числа.
Выражение вида
называется числовым рядом.
a a a a
n 1
n
1
2
3
an
аn − общий член ряда,
а1, а2, а3, … − члены ряда.
1
1
1
1
n
2
3
n 1
an
1
n
1
1
; a3 n 3
n
3
5

6.

Сумма ряда
Сумма первых n членов ряда называется n-й частичной суммой ряда и обозначается Sn,
т.е. Sn= а1+а2+…+аn.
Сумма слагаемых после Sn образует n-й остаток ряда: Rn= аn+1+аn+2+аn+3+….
Sn n 1
имеет конечный предел S при
S lim Sn
называют суммой ряда.
• Если последовательность частичных сумм ряда
n→∞, то ряд называется сходящимся, число
n
a сходится S : lim S S
n 1
• Если
n
n
n
lim Sn не существует или равен ∞, то такой ряд суммы не имеет. Говорят, что ряд
n
расходится.
6

7.

ПРИМЕРЫ РЯДОВ
1 1 1 1
n
1
предела S нет
0 S2 n 1 1 Единого
S2 n n
и ряд расходится
n
n2
Sn n
n
n 1
2
2
2
n
1
2
3
n 1
1
1 1
1
n
2 4
n 0 2
1
1 1
1
2 3
n 1 n
1
n
2
1
n
Конечного предела S нет
и ряд расходится
1
b1
1
S
2
n
n
1 q 1 1
n 0 2
2
Гармонический расходящийся ряд
Ряд сходится к 2

8.

ПРИМЕРЫ РЯДОВ
1
1 1
1
2 3
n 1 n
1
k
1
n
Гармонический расходящийся ряд
Ряд назван гармоническим, так как складывается из «гармоник»: k-я гармоника,
извлекаемая из скрипичной струны, — это основной тон, производимый струной
длиной 1/k от длины исходной струны. Кроме того, каждый член ряда, начиная со
второго, представляет собой среднее гармоническое двух соседних членов.
Cреднее гармоническое чисел есть обратная величина к среднему от обратных
к этим числам.
H ( x1 , x2 , , xn ) n
n
1
i 1 xi

9.

ПРИМЕРЫ РЯДОВ
Пример 1.
1
1 1
1
2 3
n 1 n
1
n
Рассмотрим разность частичных сумм
1
1
1
S2 n Sn
n 1 n 2 n 3
1
2n
1
1
1
2n 2n 2n
n слагаемых
о/п По определению, если ряд сходится, то
Но мы получили:
Значит, ряд расходится.
1 1
2n 2
lim Sn S , lim S 2 n S lim S 2 n S n 0.
n
n
n
1
lim S2 n Sn .
n
2

10.

ПРИМЕРЫ РЯДОВ
Пример 2. Рассмотрим ряд
Члены ряда образуют геометрическую прогрессию, поэтому сумма
первых членов находится по формуле:
1. Если |q|<1, то qn→0 при n→∞, ряд сходится и его сумма S=a/(1−q).
2. Если |q|>1, то qn→∞ при n→∞, поэтому и ряд расходится.
3. Если q = 1, то ряд примет вид: а + а + а +…
В этом случае Sn= nа ,
ряд расходится.

11.

ПРИМЕРЫ РЯДОВ
4. Если q = −1, то ряд примет вид: а − а + а −…
В этом случае Sn = 0 при четном n и Sn = а при нечетном n, поэтому
не существует и ряд расходится.
сходится при |q| < 1
расходится при |q| ≥ 1.
11

12.

ПРИМЕРЫ РЯДОВ
Пример 3. Рассмотрим ряд
1
2
n
1
n 2
1
1
A
B
2
n 1 n 1 n 1 n 1 n 1
A n 1 B n 1 1
1
2
1
n 1 2 B 1 B
2
n 1 2A 1
A
1
1 1
1
.
2
2 n 2 n 1 n 1
n 2 n 1
1 1 1 1 1 1 1 1
Sn 1
2 3 2 4 3 5 4 6
1 1 1
1
1
2 2 n n 1
1
1
1
1
1
1
n 3 n 1 n 2 n n 1 n 1
3 Ряд сходится к ¾.
S lim Sn .
n
4
12

13.

СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
1. Если к ряду
a прибавить (или отбросить)
n 1
n
конечное число членов, то исходный ряд и полученный ряд сходятся или расходятся
одновременно.
2. Если ряд
сходится и его сумма равна S, то ряд
также сходится и его сумма равна с·S.
3. Если ряды
сходятся ряды
сходятся и их суммы соответственно равны Sа и Sb, то
и их суммы соответственно равны Sа ± Sb.
13

14.

СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
4. Если an
n 1
сходится, то остаток ряда стремится к нулю.
Вспомним, что n-й остаток ряда получается путем отбрасывания n первых его
членов.
Доказательство:
a a a a
n 1
n
2
3
an an 1 an 2
Sn
a
n 1
1
n
Rn
- сходящийся S lim Sn
n
0 N : n N S n S lim Rn 0
n
Rn
14

15.

2. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Установить сходимость или расходимость ряда путем вычисления
во многих случаях является непростой задачей.
Поэтому для выяснения сходимости ряда используют специальные
признаки сходимости.
A B
Необходимое условие для А
(из А необходимо следует В)
A B
Достаточное условие для А
(для А достаточно выполнения В)
A B
Критерий
( А верно тогда и только тогда, когда верно В)
15

16.

2. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Теорема 1 (необходимый признак сходимости).
Если ряд
сходится, то предел его общего члена при n → ∞ равен нулю: lim an 0.
Доказательство.
Пусть ряд
n
сходится.
Тогда, учитывая, что an = Sn−Sn −1, получим
Следствие (достаточное условие расходимости ряда). Если предел n-го члена
ряда отличен от нуля или не существует, то ряд расходится.
16

17.

2. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Достаточные признаки сходимости
Рассмотрим некоторые достаточные признаки сходимости для
знакоположительных рядов, т.е. рядов с неотрицательными членами.
Замечание. Ряд с отрицательными членами превращается в
знакоположительный путем умножения на (−1), что, согласно свойствам
рядов, не влияет на сходимость ряда.
17

18.

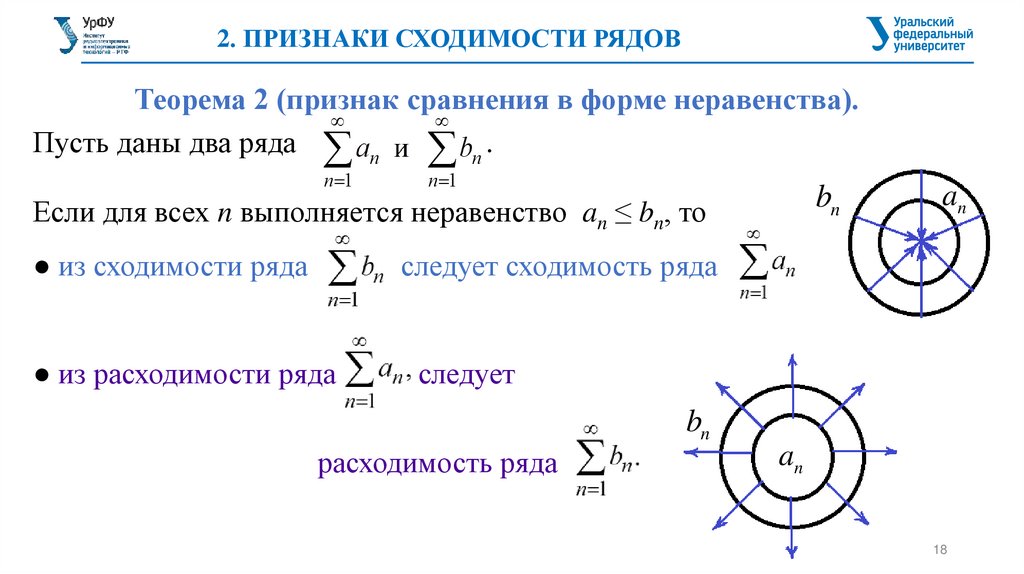
2. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Теорема 2 (признак сравнения в форме неравенства).
Пусть даны два ряда
.
bn
Если для всех n выполняется неравенство an ≤ bn, то
● из сходимости ряда
следует сходимость ряда
● из расходимости ряда
следует
an
bn
расходимость ряда
an
18

19.

ПРИМЕРЫ
Пример 1. Исследовать сходимость ряда
1
1
n
n
n 3 3
n N
1
n
- сходящийся, как сумма бесконечно убывающей геометрической
3
n 1
прогрессии.
По признаку сравнения в форме неравенства, исходный ряд тоже сходится.
19

20.

ПРИМЕРЫ
Пример 2. Исследовать сходимость ряда
n ln n n N
1
1
n N
ln n n
Так как ряд
1
расходится, то и
n 2 n
исходный ряд тоже расходится.
20

21.

2. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Теорема 3 (предельный признак сравнения).
Если
– знакоположительные ряды и существует
конечный, отличный от нуля предел
k 0, k
то ряды одновременно сходятся или расходятся.
21

22.

ПРИМЕРЫ
Пример 3. Исследовать сходимость ряда
1
Подберем ряд для сравнения. - расходящийся.
n 1 n
sin
an
2
n
lim lim
sin
n b
n
1
2n
n
n
n
lim
0
2n n 2n 2
Ряды ведут себя одинаково.
Исходный ряд расходится, как и гармоничный ряд.
22

23.

2. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Теорема 4 (признак Даламбера).
Пусть для ряда
с положительными членами существует предел
Тогда ряд сходится при k < 1 и расходится при k > 1.
!!! При k = 1 признак ответ на вопрос о сходимости ряда не дает.
Рекомендации к применению: наличие факториала, показательной функции с n в
степени (например: n!, 3n).
23

24.

ПРИМЕРЫ
Пример 4. Исследовать сходимость ряда
n 1
an 1
n 2 !
n 1
n
n
an
,
n 1 !
n
n 1
n 1 !
an 1
n
1
n
1
!
n 1
lim
lim
lim
n
n a
n n 2 !
n n 1 ! n 2
n
n
n
1
e
n 1
n 1 1
lim
1 e
n n 2
n
n
e >1, значит исходный ряд расходится.
24

25.

2. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Теорема 5 (радикальный признак Коши).
Пусть для ряда
с положительными членами существует предел
Тогда ряд сходится при k < 1 и расходится при k > 1.
При k = 1 признак ответ на вопрос о сходимости ряда не дает.
25

26.

ПРИМЕРЫ
Пример 5. Исследовать сходимость ряда
По признаку Даламбера:
n 1
an 1
2
1 n 1
lim
lim
2lim
n
1
n
n a
n
n n 2
2
n 2
n 2
n
n 1
n 2 1 n
1 n 2
1
1
1
1
2lim
1
2lim
1
n n 2
n n 2
n 2
n 2
n
n
n
2
1
lim
0
n
e
n 2
0 < 1, значит ряд сходится.
По радикальному признаку Коши:
2n
2
lim an lim n
lim
0 1
n
n
n
n 1 n n 1
n
ряд сходится.
26

27.

2. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Теорема 6 (интегральный признак Коши).
Пусть члены знакоположительного ряда
являются значениями некоторой непрерывной монотонно убывающей на
промежутке [1; +∞) функции f(x) так, что a1 = f(1), a2 = f(2),…, an = f(n),...
Тогда
1)если
сходится, то сходится и ряд
2) если
расходится, то и ряд
расходится.
27

28.

ПРИМЕРЫ
сходится при > 1 и расходится при ≤ 1.
Пример 6. Доказать, что ряд
1
Рассмотрим функцию f ( x) - монотонно убывающую на отрезке 1; .
x
1
dx x
1 x 1 , 1.
1
α <1, тогда 1-α >0 и интеграл равен бесконечности, то есть расходится одновременно с
рядом.
1
1 1
1
α >1, тогда 1-α <0 и интеграл равен
1
,
1
x 1 1
1 1
то есть расходится одновременно с рядом.
28

29.

ПРИМЕРЫ
Пример 7. Исследовать сходимость ряда
Условия теоремы об интегральном признаке Коши выполнены.
d ln x 1
dx
1 x 1 ln x 1 1 ln x 1 ln ln x 1 1
Интеграл расходится одновременно с рядом.
29

30.

ПРИМЕРЫ
n
n n 1
n 1
3
5
n2 n
6n 7 n 1
n 2
3
15
1
n tg
n
n 1
1
n
2
Ряд расходится
1
3
n 1 n
Ряд сходится
n 1
3
1
n tg 1 0, n
n
Ряд расходится