LEKTsIYa_integralnoe ischislenie_DBUgms

1. Интегральное исчисление

Высшая математика
Голиков Руслан Юрьевич,
к.т.н., доцент
1

2. Задача, обратная дифференцированию

3. Задача, обратная дифференцированию

h
Чтобы найти закон перемещения падающего тела h(t) по известному
закону его скорости v(t)=gt, надо подобрать функцию такого вида,
что если мы ее продифференцируем, то опять получим функцию
v t gt
скорости, т.е. v(t)=gt. Поэтому все, что мы делаем при
v t h t
дифференцировании таких функций, сделаем наоборот, начиная с
конца. Если показатель степени надо было уменьшать на единицу мы его увеличим на единицу. Если основание надо было умножать
на старый показатель степени - мы поделим его на новый:
t 1+1=2
gt 2
v t gt g
h t
2
2
Если мы продифференцируем эту функцию, то получим исходную функцию:
gt 2 1
1
2
h t
g t g 2t gt v t .
2
2 2
gt 2
, полученную по известной ее производной v t gt,
Поэтому неизвестную функцию h t
2
называют первообразной.

4. Понятие первообразной

ОПРЕДЕЛЕНИЕ 1. Функция F(x) называется первообразной от функции f(x) на отрезке
[a, b], если во всех точках этого отрезка выполняется равенство F΄(x)=f(x).
ПРИМЕР. Найти первообразную от функции f(x)=х3.
Из определения первообразной следует, что мы должны отыскать такую функцию,
чтобы при ее дифференцировании получить х3. При дифференцировании такой
функции мы умножаем х на показатель степени, а потом уменьшаем показатель
степени на единицу. Следовательно, при отыскании первообразной мы должны
поступить наоборот: показатель степени увеличить на единицу, а х разделить на это
число, чтобы при дифференцировании дробь сократилась. Значит, искомая функция
будет иметь вид F(x)=х4/4, а ее производная будет: F΄(x)=(х4/4)΄=1/4∙4 ·х4-1=х3. А также:
F΄(x)=(х4/4+3)΄=х3, F΄(x)=(х4/4-5)΄=х3, … или F(x)=х4/4+С, где С – произвольная постоянная.
ТЕОРЕМА : Если F1(x) и F2(x) – две первообразные от функции f(x) на отрезке[a, b], то
разность между ними равна постоянному числу: F1(x) - F2(x)=С.
* Иными словами, все первообразные от функции f(x) отличаются друг от друга на некоторую
постоянную величину С.

5. Неопределенный интеграл

ОПРЕДЕЛЕНИЕ 2: Если функция F(x) является первообразной для функции f(x), то
выражение F(x)+С называется неопределенным интегралом от функции f(x) и
обозначается символом ∫f(x)dx. Таким образом, по определению
∫ f(x)dx = F(x) + С,
если F΄(x)=f(x).
∫ - знак неопределенного интеграла;
f(x) - подынтегральная функция;
f(x)dx - подынтегральное выражение;
С - постоянная интегрирования.
Подынтегральное выражение представляет собой дифференциал:
Если F΄(x)=f(x), то f(x)dx =F΄(x)dx=dF (x) (дифференциал)

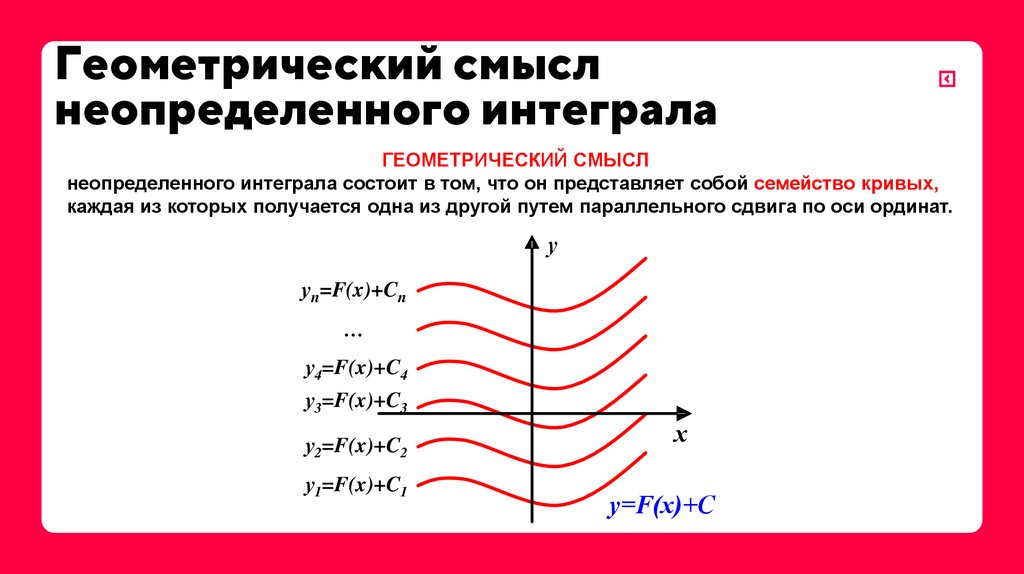
6. Геометрический смысл неопределенного интеграла

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
неопределенного интеграла состоит в том, что он представляет собой семейство кривых,
каждая из которых получается одна из другой путем параллельного сдвига по оси ординат.
у
уn=F(x)+Cn
…
у4=F(x)+C4
у3=F(x)+C3
у2=F(x)+C2
у1=F(x)+C1
х
у=F(x)+C

7. Связь дифференциала и неопределенного интеграла

ТЕОРЕМА (о непрерывности дифференцируемой функции):
Если функция f(x) дифференцируема в каждой точке отрезка [a, b], то она на этом
отрезке непрерывна.
Следствие: всякую непрерывную на отрезке [a, b] функцию f(x) мы можем
рассматривать в качестве производной от некоторой другой непрерывной
функции F(x), т.к. F΄(x)=f(x).
Иными словами, у всякой непрерывной функции f(x) имеется первообразная F(x).

8. Таблица основных интегралов

1. dx x С.
6. sin xdx cos x C.
x n 1
2. x dx
C (n 1).
n 1
7. cos xdx sin x C.
dx
arctgx C .
12.
2
1 x
dx
arcsin x C .
13.
2
1 x
8. tgxdx ln | cos x | C.
dx
1
x
arctg
C.
14. 2
2
x a
a
a
9. ctgxdx ln | sin x | C.
dx
1
x a
ln
C.
15. 2
x a 2 2a x a
dx
ctgx C .
10.
2
sin x
dx
1 a x
ln
C.
16. 2
2
a x
2a a x
n
dx
ln | x | C х 0 .
3.
x
x
a
x
C,
4. a dx
ln a
где a 0 и a 1.
5. e dx e C.
x
x
dx
tgx C .
11.
2
cos x

9. Свойства неопределенного интеграла

СВОЙСТВО 1. Неопределенный интеграл от алгебраической суммы двух или нескольких
функций равен алгебраической сумме интегралов:
∫ ( f1(x)+f2(x)+f3(x))dx = ∫ f1(x)dx + ∫ f2(x)dx + ∫ f3(x)dx
СВОЙСТВО 2. Постоянный множитель можно выносить за знак интеграла, т.е. если a = const, то:
∫а f(x)dx=а∫ f(x)dx
ПРАВИЛА ИНТЕГРИРОВАНИЯ СОСТАВНЫХ ТАБЛИЧНЫХ ФУНКЦИЙ:
1
1. f (ax )dx F (ax ) C
a
2. f ( x b)dx F ( x b) C
1
3. f (ax b)dx F (ax b) C
a

10. Метод непосредственного интегрирования

ПРИМЕР 1. Вычислить неопределенный интеграл:
x4 5 x3 3x2
( 2 x 5 x 3 x 4 )dx 2 x dx 5 x dx 3 xdx 4 dx 2 3 2 4 x C
3
2
3
2
Проверка решения дифференцированием:
x4 5 x3 3x2
1
5
3
4 x C 4 х 3 3 х 2 2 х 4 2 х 3 5 х 2 3 х 4
3
2
2
3
2
2
ПРИМЕР 2. Вычислить неопределенный
интеграл:
3
1
2
x2 2x 2
x2 2
x2 2
3
x x dx xdx x dx 2 3 C 2 3 x C 2 3 x x C
Проверка решения дифференцированием:
3
1
x2 2
1
2 2
2
x x C 2 х ( х ) х х х х
2
3
2 3

11. Метод непосредственного интегрирования

5x
5x
ПРИМЕР 3. Вычислить неопределенный интеграл: e a dx
e a dx e dx a dx.
5x
5x
5x
5x
(Используем Свойство 1)
1 5x
x
x
5x
e
dx
e
С
e
dx
e
С
5
(Используем Правило 1)
x
5x
a
1a
x
5x
a
dx
С
a
dx
С
ln a
5 ln a
e5 x
a5 x
1 5 x a5 x
5x
5x
e
a
dx
C
e
C
5 5ln a
5
ln a
ПРИМЕР 4. Вычислить неопределенный интеграл:
dx
ln
|
x
|
C
x
dx
1
3 x 7 3 ln | 3 x 7 | C (Используем Правило 3)
dx
3x 7
1
3
1
1
1
.
ln | 3 x - 7 | C ln 3 x - 7
3 3x - 7 3x - 7
3
3
1
u 3 x - 7 yu ln u ; u x 3 x - 7 3;
u
3
3
y x yu u x
.
u 3x - 7

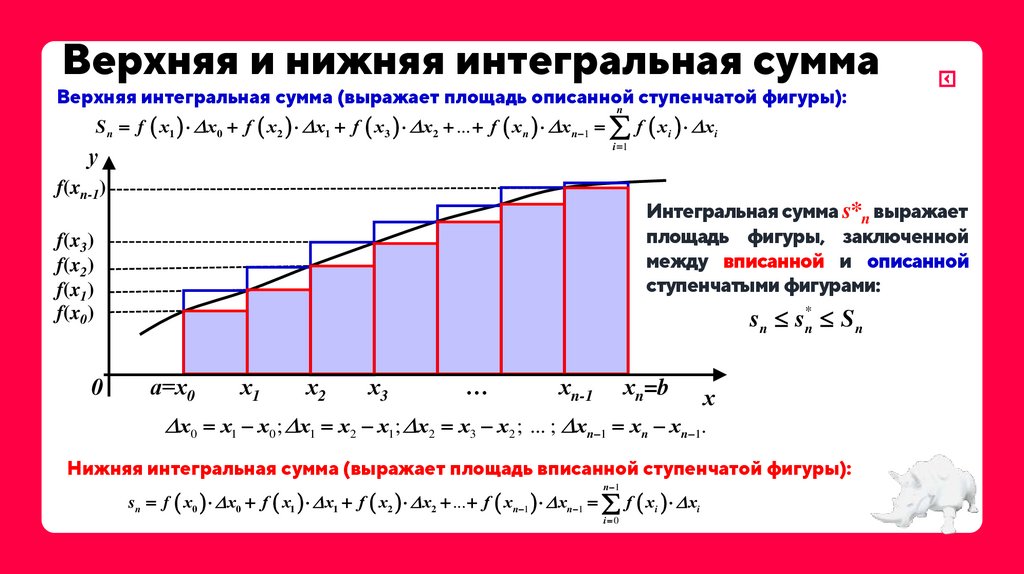
12. Верхняя и нижняя интегральная сумма

Верхняя интегральная сумма (выражает площадь описанной ступенчатой фигуры):
n
Sn f х1 х0 f х2 х1 f х3 х2 ... f хn хn 1 f х i х i
i 1
у
f(xn-1)
Интегральная сумма s*n выражает
площадь фигуры, заключенной
между вписанной и описанной
ступенчатыми фигурами:
f(x3)
f(x2)
f(x1)
f(x0)
0
sn sn* Sn
а=х0
х1
х2
х3
…
хn-1
хn=b
х
х0 х1 х0 ; х1 х2 х1; х2 х3 х2 ; ... ; хn 1 хn хn 1.
Нижняя интегральная сумма (выражает площадь вписанной ступенчатой фигуры):
n 1
sn f х0 х0 f х1 х1 f х2 х2 ... f хn 1 хn 1 f хi хi
i 0

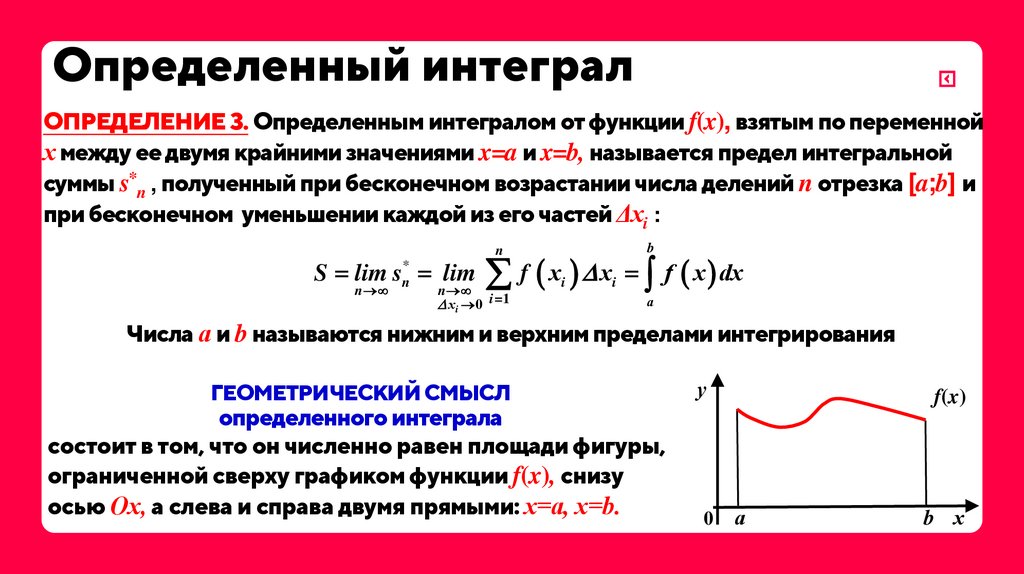
13. Определенный интеграл

ОПРЕДЕЛЕНИЕ 3. Определенным интегралом от функции f(x), взятым по переменной
х между ее двумя крайними значениями x=a и x=b, называется предел интегральной
суммы s*n , полученный при бесконечном возрастании числа делений n отрезка [a;b] и
при бесконечном уменьшении каждой из его частей Δxi :
n
b
хi 0 i=1
а
S lim sn* lim f хi хi f х dх
n
n
Числа а и b называются нижним и верхним пределами интегрирования
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
определенного интеграла
состоит в том, что он численно равен площади фигуры,
ограниченной сверху графиком функции f(x), снизу
осью Ох, а слева и справа двумя прямыми: х=а, х=b.
у
0
f(x)
а
b х

14. Определенный интеграл

ТЕОРЕМА. Если F(x) есть какая-либо
первообразная от непрерывной
функции f(x), то справедлива формула:
b
f ( x )dx F ( x )| F ( b ) F ( a )
b
a
a
Формула Ньютона-Лейбница
Готфрид Вильгельм Лейбниц
1646 – 1716 г.г.
Исаак Ньютон
1642 – 1727 г.г.
b
| - знак двойной подстановки
a

15. Свойства определенного интеграла

СВОЙСТВО 1. Определенный интеграл от алгебраической суммы двух или нескольких функций
равен алгебраической сумме определенных интегралов:
b
b
b
b
f ( x) f ( x) f ( x) dx f ( x )dx f ( x )dx f ( x )dx
1
2
2
a
1
2
а
a
3
а
СВОЙСТВО 2. Постоянный множитель можно выносить за знак интеграла, т.е. если a = const, то:
b
b
a
а
аf ( x)dx а f ( x)dx
СВОЙСТВО 3. При перестановке пределов интегрирования определенный интеграл меняет знак на
b
а
противоположный:
f ( x )dx f ( x )dx
a
b
СВОЙСТВО 4. Если функция f(x) интегрируема на наибольшем из отрезков [a;b], [a;с] и [с;b], то
она интегрируема и на двух других отрезках. Если [a;с] и [с;b] ϵ [a;b], то:
b
с
b
a
а
с
f ( x)dx f ( x)dx f ( x)dx
а
СВОЙСТВО 6. Если a = b, то:
f ( x )dx 0
a

16. Вычисление определенного интеграла

ПРИМЕР 1. Вычислить определенный интеграл:
2
x5 2 1 5 5
1
31
1 x dx 5 |1 5 (2 1 ) 5 32 1 5 .
4
ПРИМЕР 2. Вычислить определенный интеграл:
2
sin xdx cos x| (cos 2 cos 0) (0 1) 1.
2
0
0
ПРИМЕР 3. Вычислить определенный интеграл:
а
а
dx
1
1
1
ln(2
x
1)
[ln(2
а
1)
ln1]
ln(2а 1). (Используем Правило 3)
|1 2
1 2 x 1 2
2

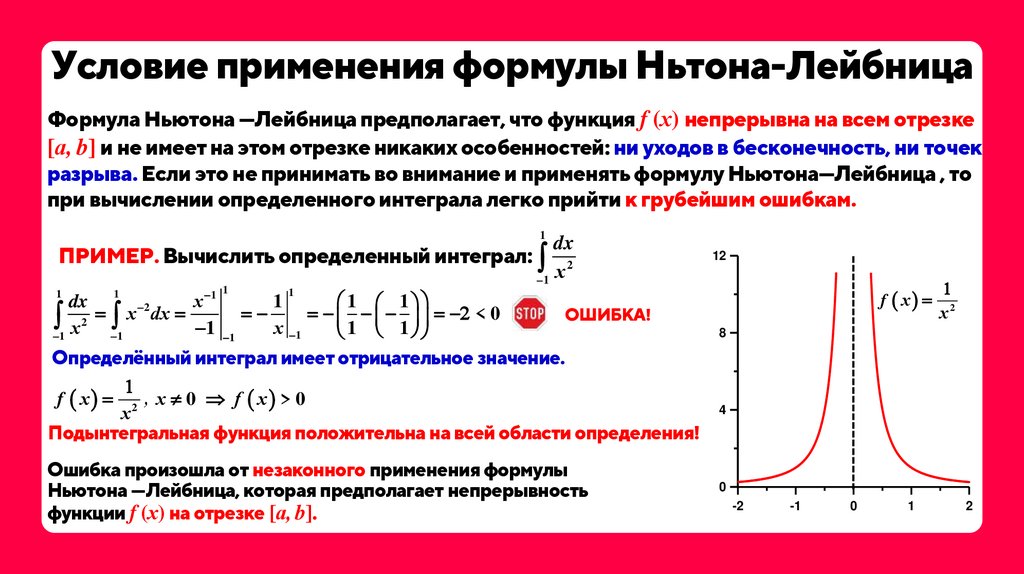
17. Условие применения формулы Ньтона-Лейбница

Формула Ньютона —Лейбница предполагает, что функция f (х) непрерывна на всем отрезке
[а, b] и не имеет на этом отрезке никаких особенностей: ни уходов в бесконечность, ни точек
разрыва. Если это не принимать во внимание и применять формулу Ньютона—Лейбница , то
при вычислении определенного интеграла легко прийти к грубейшим ошибкам.
1
dx
х2
1
ПРИМЕР. Вычислить определенный интеграл:
1
dx
х 1
1
1 1
2
х
dx
1 1 < 0
1 х 2 1
1 1
х 1
1
1
12
f х
1
ОШИБКА!
Определённый интеграл имеет отрицательное значение.
f х 2 , х 0 f х > 0
х
Подынтегральная функция положительна на всей области определения!
Ошибка произошла от незаконного применения формулы
Ньютона —Лейбница, которая предполагает непрерывность
функции f (х) на отрезке [а, b].
х2
8
4
0
-2
-1
0
1
2

18. Приложения определенного интеграла

ПРИМЕР 1: Вычислить площадь фигуры, ограниченной линиями:
-1
0
х2
у=, х1 = -1, х2 = 1.
2
1
-1
1
1
х2
1 х3
1 3
1
1
1 1
3
1 2 dх 2 3 1 6 1 1 6 2 3 S = 3 3 .
ФИГУРА НИЖЕ ОСИ Ох

19. Приложения определенного интеграла

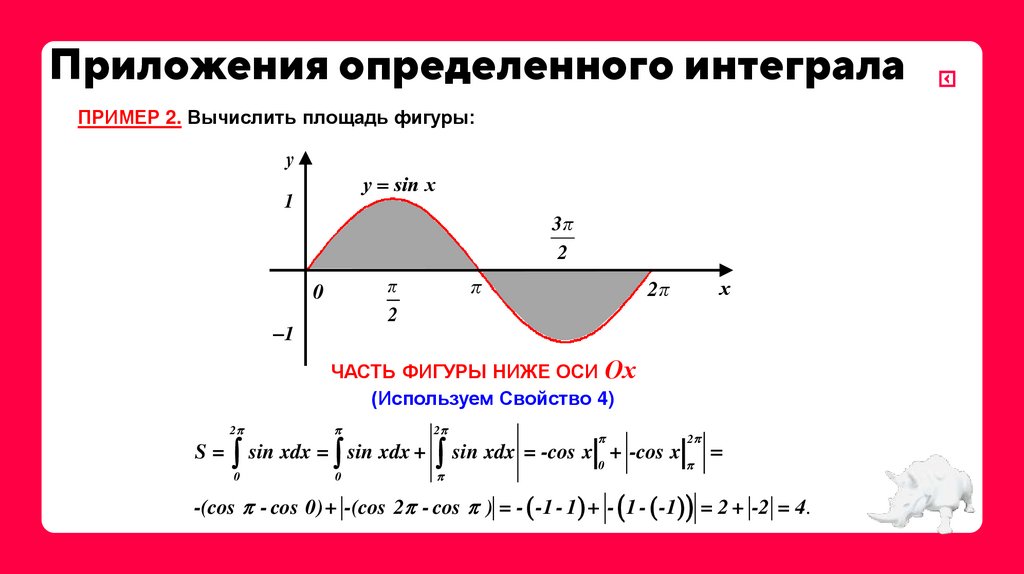
ПРИМЕР 2. Вычислить площадь фигуры:
у
у sin х
1
3π
2
π
2
0
1
π
х
2π
ЧАСТЬ ФИГУРЫ НИЖЕ ОСИ Ох
(Используем Свойство 4)
2
2
2
0
S = sin xdx = sin xdx + sin xdx = -cos x| + -cos x|
0
0
-(cos - cos 0)+ -(cos 2 - cos ) = - -1 - 1 + - 1 - -1 = 2 + -2 = 4.

20. Приложения определенного интеграла

ПРИМЕР 3: Вычислить площадь фигуры, ограниченной линиями: у = х , у =
х.
Находим точки пересечения кривых (пределы интегрирования):
1
х =
х х х = х х =
х = х х = х = = .
0
1
S
а = х = b = х = .
b
S = f х - f х dx
а
3
х х
х - х dx = х dx - х 2dx =
- - -

21. Вычисление объемов тел вращения

х=а
Si-1(xi-1)
Si (xi)
Si+1(xi+1)
xi-1
xi
xi+1
S( х) r 2 у2 f 2 ( х)
b
b
b
а
а
а
V = S х dx = f 2 х dx = f 2 х dx
х=b
x

22. Вычисление объемов тел вращения

ПРИМЕР 1: Вычислить объем тела, образованного вращением прямой у=х+1 на
участке х1=1, х2=2.
ОБЪЕМ УСЕЧЕННОГО КОНУСА (Геометрическая формула):
у
3
2
1
-1
0
b
V = f
а
1
2
2
1
1
1
1
r12 h1 r2 2 h2 3 2 3 2 2 2 =
3
3
3
3
1
19
1
= 27 - 8 = = 6 .
3
3
3
V=
х dx х + 1
1
х
2
2
2
2
2
2
dx = х + 2х + 1 dx = х dx + 2х dx + dx =
1
1
1
1
2
2
2
23
х3
13
1
8 1
19
2
2
2
х х + 2 + 2 + 1 + 1 - + 4 + 2 - 1 - 1 = 6 .
3
3 3
3
3
1
3
3

23. Вычисление объемов тел вращения

ПРИМЕР 2: Линия, ограниченная полуволной синусоиды y=sinx и осью Ох
вращается вокруг оси Ох. Найти объем тела вращения.
у
1
0
-1
y=sinx
1 1
V sin2 xdx cos 2 x dx dx cos 2 xdx
2 2
20
20
0
0
π
х
x
1
2
2
sin2 x|
sin2 sin0
.
|
2
22
2 4
2
0
0

24. КРОССВОРД Математический анализ