L12_Equilibrium_2025_11_24

1.

Общая Физика. Механика
Лекция 12
Условия равновесия и движение тел
вблизи положения равновесия
Лектор:
Профессор НИЯУ МИФИ
Ольчак Андрей Станиславович(

2.

Ддвижение тв. тела. Итоги:
Комбинированное движение: сочетание поступательного и
вращательного. Для его полного описания нужны 1-3 координаты
центра масс и от одной до трех угловых координат, причем скорости и
ускорения для любой точки тела складывается из 2-х компонент:
v = vc+[ω, r]
w = wc+[β, r]
vc и wc – скорость и ускорение поступат. движения центра масс тела.
r - радиус-вектор точки относительно центра масс тела
Кинетическая энергия комбинированного движения тв. тела:
T = Izω2/2 + mvc2/2
Комбинированное движение определяют два уравнения движения::
1. Уравнение движения центра масс: mwc = mdvc/dt = ΣF
2. Уравнение моментов для вращения вокруг оси 0Z, проходящей через
центр масс: dM/dt = ΣNBH или dMZ/dt = IZ dω/dt = ΣNZ
..

3.

Свободное движение твердого тела
При свободном движении твердого тела связь векторов угловой
скорости и момента импульса усложняется
Mi= Iijωj
Iij =
Ixx
Iyх
Izx
Ixy
Iyy
Izy
Ixz
Iyz
Izz
тензор (матрица)
моментов инерции
Mx= Ixх ωx + Ixy ωy + Ixz ωz
My= Iyх ωx + Iyy ωy + Iyz ωz
Mz= Izх ωx + Izy ωy + Izz ωz

4.

Свободное движение твердого тела
Если тело имеет оси симметрии, и если направить оси координат x, y,
z вдоль осей симметрии, тензор инерции может стать диагональным
Ixx
0
0x
0
Iyy
0
0
0
Izz
Mx= Ixх ωx
My= Iyy ωy
Mz= Izz ωz
Mi= Iiiωi
Для “самых симметричных” тел (сфера, шар) Ixx = Iyy = Izz = I; M= Iω
Свободно движущееся тело всегда вращается вокруг
оси, проходящей через центр масс тела. Оси вращения
несимметричных тел, как правило, не устойчивы. У
симметричных тел могут быть т.н. главные оси
симметрии, вращение вокруг которых может быть
устойчиво. «Самые главные» оси те, вращение вокруг
которых всегда устойчиво.

5. ГИРОСКОПЫ

Гироскоп = массивное, осесимметричное тело,
вращающееся вокруг оси симметрии с большой
угловой скоростью Ω. При этом момент импульса
гироскопа устойчиво сохраняется: M = IzΩ = Const
Гироскопический эффект: если к оси гироскопа
приложить силу F , ось гироскопа смещается в
направлении момента этой силы,
Ось симметрии гироскопа начинает сама вращаться
(прецессировать) вокруг направления действующей
силы с некоторой угловой скоростью ω << Ω,
Причем: ω ~ 1/ Ω,
С уменьшением скорости вращения гироскопа начинаются
нутации (колебания направления оси симметрии) и
движение теряет устойчивость.

6.

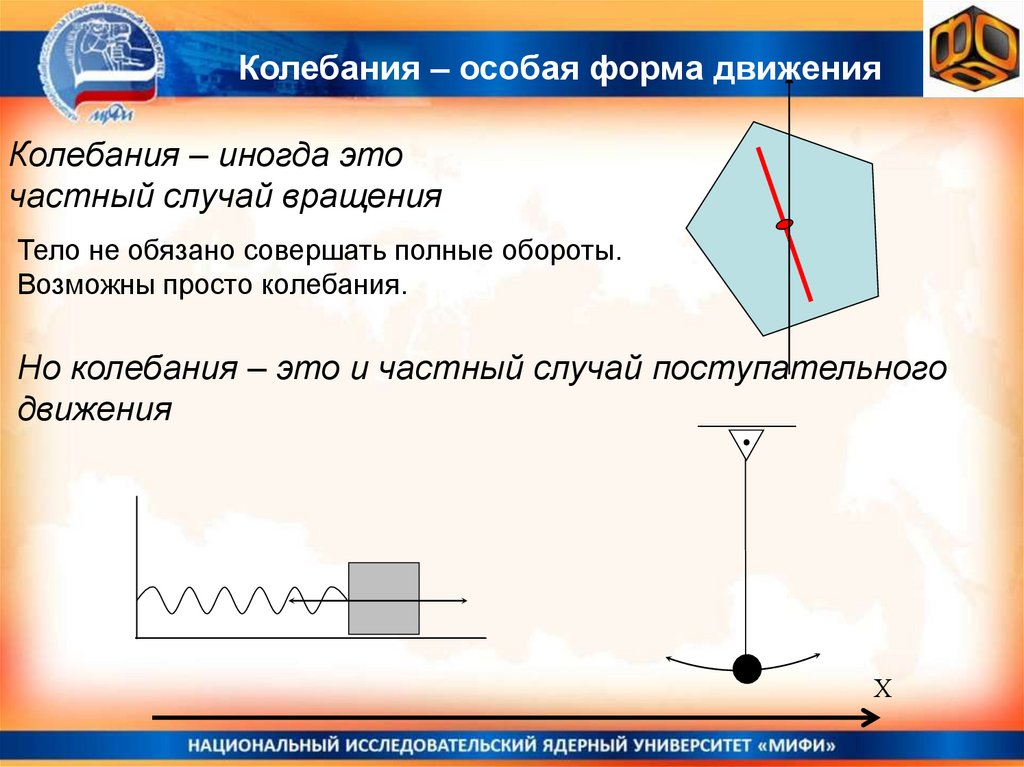
Колебания – особая форма движения
Колебания – иногда это
частный случай вращения
Тело не обязано совершать полные обороты.
Возможны просто колебания.
Но колебания – это и частный случай поступательного
движения
Х

7.

Колебания
x
t
x
T
T
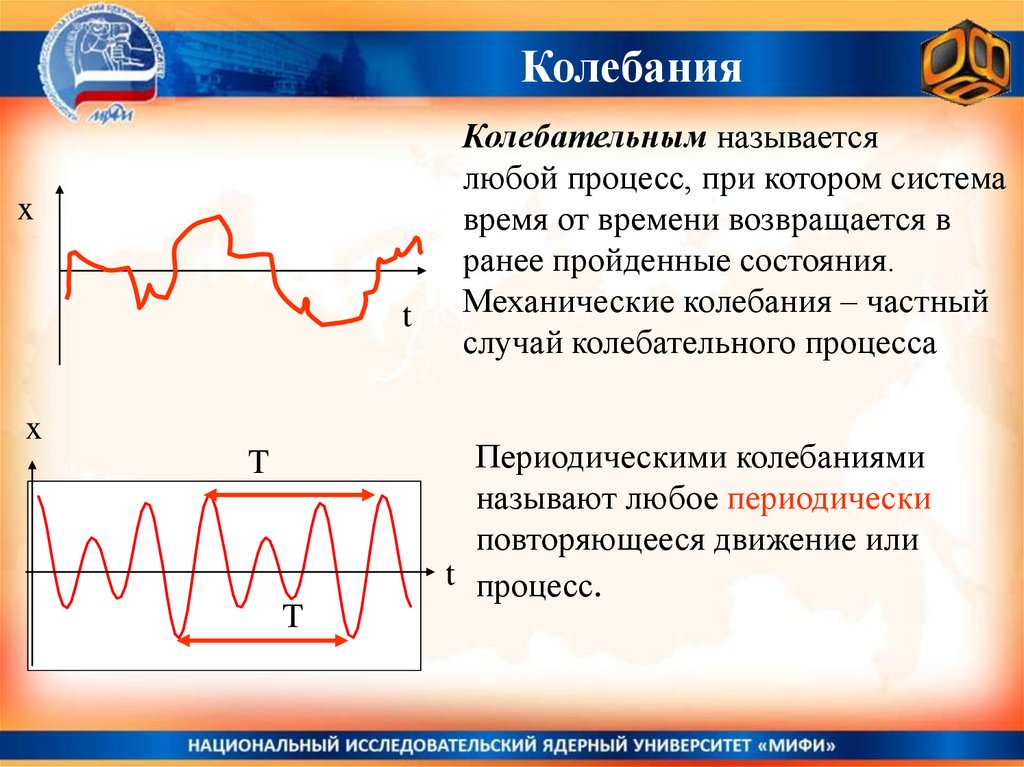
Колебательным называется
любой процесс, при котором система
время от времени возвращается в
ранее пройденные состояния.
Механические колебания – частный
случай колебательного процесса
Периодическими колебаниями
называют любое периодически
повторяющееся движение или
t процесс.

8.

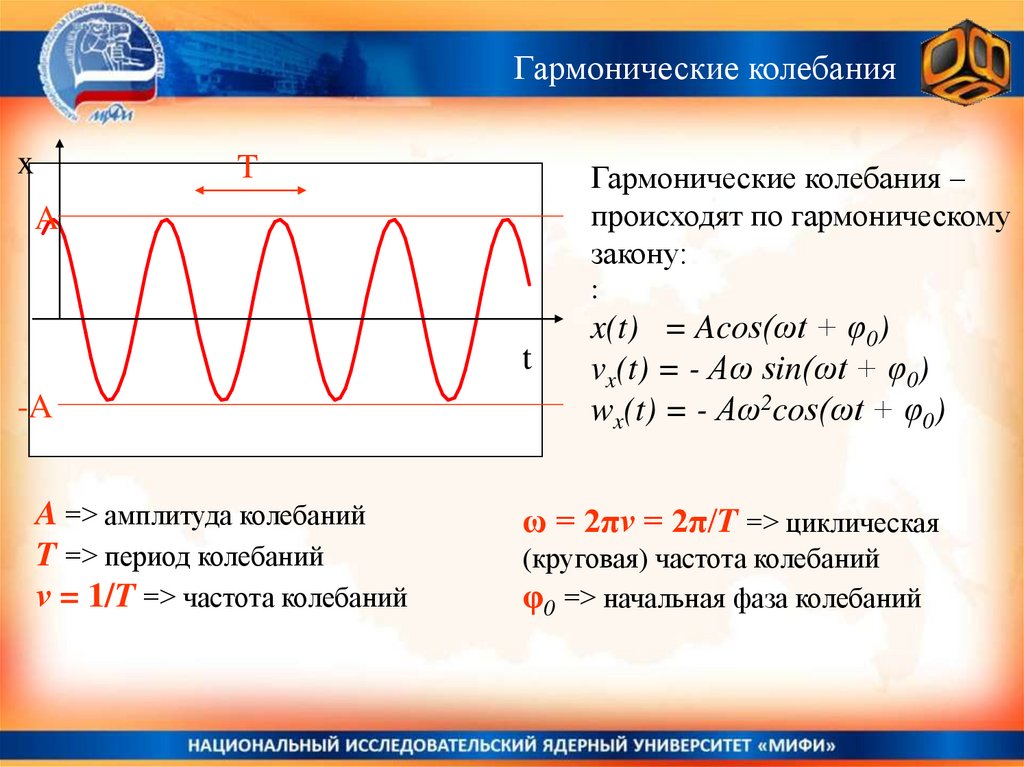
Гармонические колебания
x
T
Гармонические колебания –
происходят по гармоническому
закону:
A
:
t
-A
A => амплитуда колебаний
T => период колебаний
ν = 1/T => частота колебаний
x(t) = Acos(ωt + φ0)
vx(t) = - Aω sin(ωt + φ0)
wx(t) = - Aω2cos(ωt + φ0)
ω = 2πν = 2π/T => циклическая
(круговая) частота колебаний
φ0 => начальная фаза колебаний

9.

Гармонические колебания
Производные любого порядка от гармонической
функции – тоже гармонические функции.
положения x(t)
скорости v(t)
ускорения w(t)
x(t) = Acos(ωt + φ0)
vx(t) = - Aω sin(ωt + φ0)
wx(t) = - Aω2cos(ωt + φ0)
9

10.

Сходство математического описания
колебаний и вращения
ω
φ0 + ωt
R
φ0
φ = φ0 + ωt
x(t) = Rcos(ωt + φ0),
y(t) = Rsin(ωt + φ0),
Подробнее об особенностях колебательного движения –
во втором семестре

11.

Условие равновесия для мат. точки
Колебания возникают при отклонении системы от положения
устойчивого равновесия.
Для мат. точки условие равновесия = равенство нулю суммы сил
на нее действующих: ΣF = 0.
Этому условию всегда отвечает состояние покоя (v = Const)
(равномерное прямолинейное движение в ИСО), но нас интересуют
Системы, имеющие точки равновесия устойчивого,
В потенциальном поле сил U(r) на мат. точку действует сила
F = grad U(r), которая может равняться нулю в отдельных точках –
экстремумах функции U(r) ,
Напоминание: grad U = i дU/дх + j дU/дy + k дU/дz

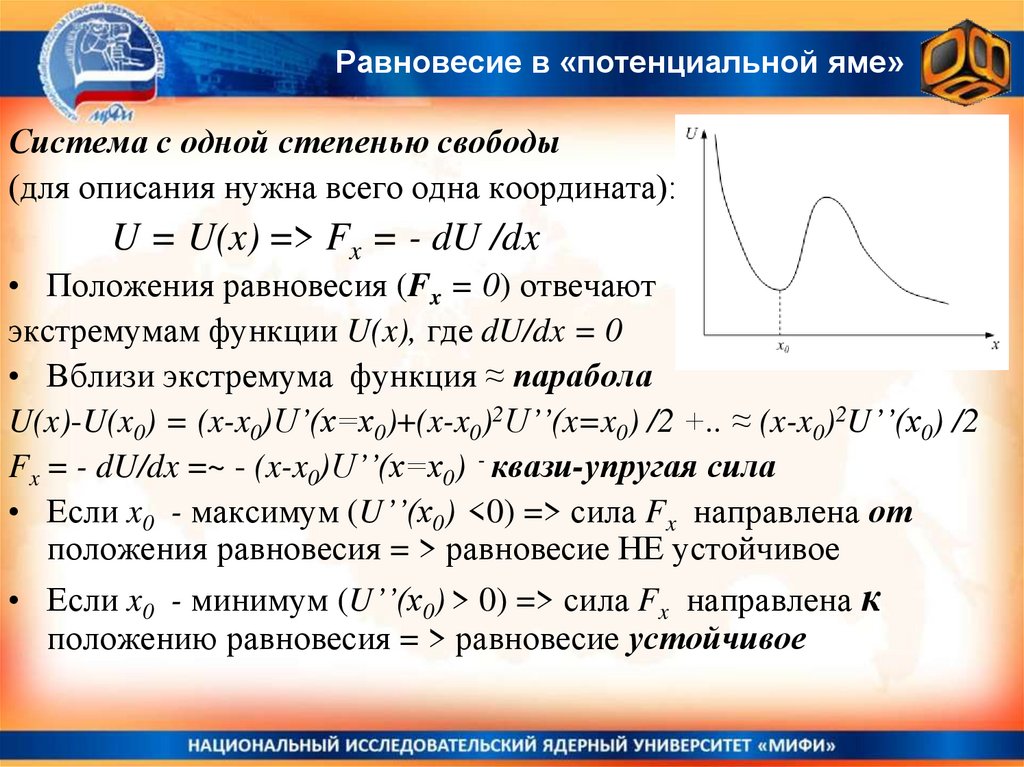
12. Равновесие в «потенциальной яме»

Система с одной степенью свободы
(для описания нужна всего одна координата):
U = U(x) => Fx = - dU /dx
• Положения равновесия (Fx = 0) отвечают
экстремумам функции U(x), где dU/dx = 0
• Вблизи экстремума функция ≈ парабола
U(x)-U(x0) = (x-x0)U’(x=x0)+(x-x0)2U’’(x=x0) /2 +.. ≈ (x-x0)2U’’(x0) /2
Fx = - dU/dx =~ - (x-x0)U’’(x=x0) - квази-упругая сила
• Если x0 - максимум (U’’(x0) <0) => сила Fx направлена от
положения равновесия = > равновесие НЕ устойчивое
• Если x0 - минимум (U’’(x0) > 0) => сила Fx направлена к
положению равновесия = > равновесие устойчивое

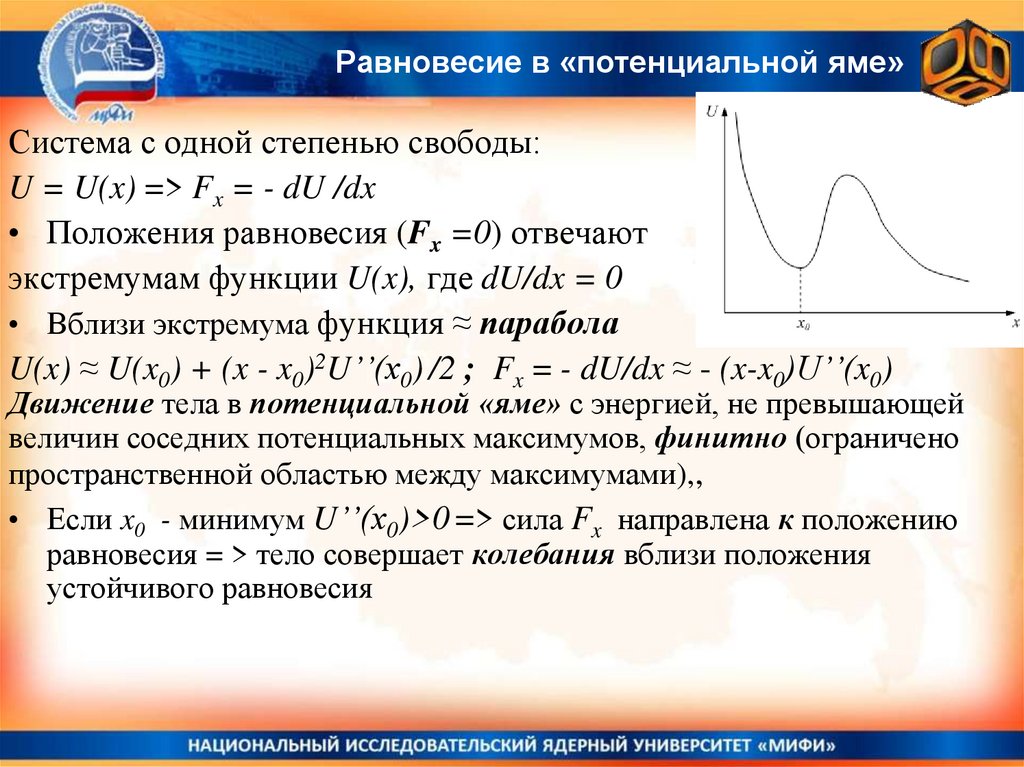
13. Равновесие в «потенциальной яме»

Система с одной степенью свободы:
U = U(x) => Fx = - dU /dx
• Положения равновесия (Fx =0) отвечают
экстремумам функции U(x), где dU/dx = 0
• Вблизи экстремума функция ≈ парабола
U(x) ≈ U(x0) + (x - x0)2U’’(x0) /2 ; Fx = - dU/dx ≈ - (x-x0)U’’(x0)
Движение тела в потенциальной «яме» с энергией, не превышающей
величин соседних потенциальных максимумов, финитно (ограничено
пространственной областью между максимумами),,
• Если x0 - минимум U’’(x0)>0 => сила Fx направлена к положению
равновесия = > тело совершает колебания вблизи положения
устойчивого равновесия

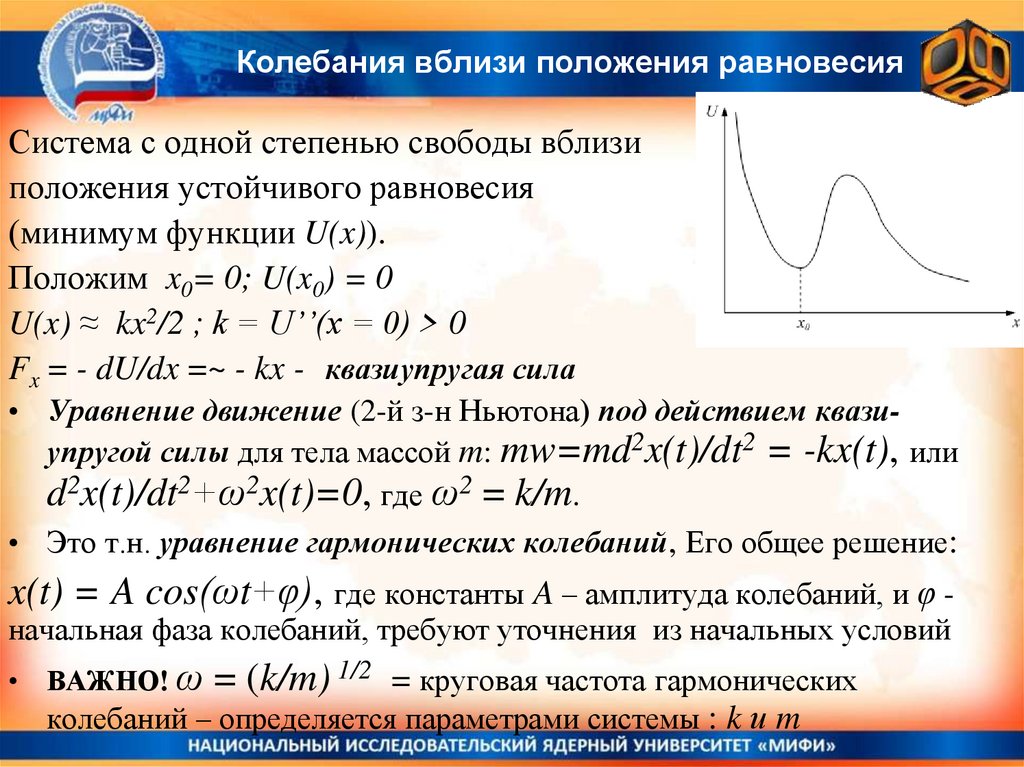
14. Колебания вблизи положения равновесия

Система с одной степенью свободы вблизи
положения устойчивого равновесия
(минимум функции U(x)).
Положим x0= 0; U(x0) = 0
U(x) ≈ kx2/2 ; k = U’’(x = 0) > 0
Fx = - dU/dx =~ - kx - квазиупругая сила
• Уравнение движение (2-й з-н Ньютона) под действием квазиупругой силы для тела массой m: mw=md2x(t)/dt2 = -kx(t), или
d2x(t)/dt2+ω2x(t)=0, где ω2 = k/m.
• Это т.н. уравнение гармонических колебаний, Его общее решение:
x(t) = A cos(ωt+φ), где константы A – амплитуда колебаний, и φ начальная фаза колебаний, требуют уточнения из начальных условий
• ВАЖНО! ω = (k/m) 1/2 = круговая частота гармонических
колебаний – определяется параметрами системы : k и m

15. Колебания вблизи положения равновесия

Система вблизи положения устойчивого равновесия:
Fx = - dU/dx =~ - kx - квази-упругая сила
ВАЖНО! В любой системе, где потенциальная энергия U(x) = kx2/2
(параболическая функция), неизбежно возникает квази-упругая сила
F = -kx , приводящая к появлению гармонических колебаний с
круговой частотой ω = (k/m)1/2. Это так для систем и сил любой природы
Решение уравнения колебаний – гармоническая функция:
x(t) = A cos(ωt+φ), где требуют уточнения константы A –
амплитуда колебаний, и φ - начальная фаза колебаний.
Эквивалентные формы записи гармонической функции:
x(t) = A cos(ωt) + В sin (ωt)
x(t) = A exp (iωt) + В exp (-ωt)
x(t) = A exp (iωt + φ)

16.

Гармонические колебания
Производные любого порядка от гармонической
функции – тоже гармонические функции.
положения x(t)
скорости v(t)
ускорения w(t)
x(t) = Acos(ωt + φ0)
vx(t) = - Aω sin(ωt + φ0)
wx(t) = - Aω2cos(ωt + φ0)
16

17. Энергия гармонических колебаний

x(t) = A cos(ω0 t + φ0)
v(t) = x’(t) =-Aω0 sin(ω0 t +φ0) =Aω0 cos(ω0 t +φ0+π/2
w(t) = x’’(t) = -Aω02 cos (ω0 t +φ0) =Aω02 cos(ω0 t+π)
T = mv2/2 = mA2ω02 sin2(ω0 t + φ0)/2
U = kx2/2 = kA2cos2(ω0 t + φ0)/2
E = mA2(ω02 sin2(ω0 t + φ0) + (k/m)cos2(ω0 t + φ0))/2
k/m = ω02
E = mA2ω02(sin2(ω0 t+φ0)+cos2(ω0 t+φ0))/2=mA2ω02/2
E = mA2ω02/2 =mvmax2/2 = kA2/2 = Const
17

18.

Механические колебательные системы
Пружинный маятник - тело массы m на
пружине жесткостью k
U(x) = kx2/2 ; F = -kx
Тело совершает гармонические колебания с
параметрами: :ω = 2πν = (k/m)1/2
ν = 1/ 2π(m/k)1/2 T = 2π(m/k)1/2
Груз на пружине, подвешенный вертикально:
U(x) = kx2/2 - mgx = k(x - х0 )2/2 - (mg)2/2k
х0 = mg/k – новое положение равновесия, U 0 = -(mg)2/2k – новый уровень
отсчета потенциальной энергии. Частоты и период колебаний те же:
ω = 2πν = (k/m)1/2
ν = 1/ 2π(m/k)1/2
T = 2π(m/k)1/2
Маятник на наклонной плоскости (без трения) будет совершать гармонические
колебания с теми же параметрами: :

19.

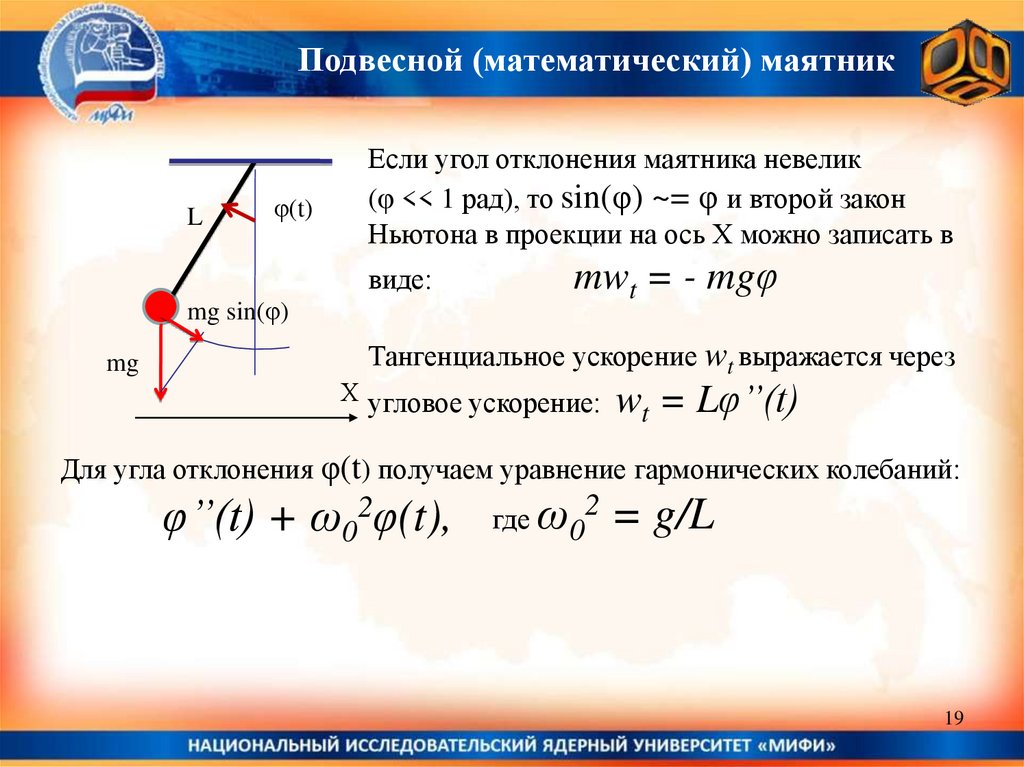
Подвесной (математический) маятник
L
φ(t)
Если угол отклонения маятника невелик
(φ << 1 рад), то sin(φ) ~= φ и второй закон
Ньютона в проекции на ось Х можно записать в
виде:
mg sin(φ)
mg
mwt = - mgφ
Тангенциальное ускорение wt выражается через
Х угловое ускорение: w = Lφ’’(t)
t
Для угла отклонения φ(t) получаем уравнение гармонических колебаний:
φ’’(t) + ω02φ(t),
где ω02 = g/L
19

20.

Подвесной (физический) маятник
o
L
C
m
Физический маятник - массивное тело, совершающее
(небольшие) колебания относительно оси подвеса
Полная энергия колебаний физического маятника равна:
E = T+U =Izω2/2+mgL(1-cosφ) = Const
dE/dt = Izφ’’(t) φ’(t) +mgL sin(φ(t)) φ’(t) = 0
Если φ<<1 => sin φ ~= φ
Мы снова получаем уравнение гармонических колебаний
с круговой частотой ω02 = mgL/Iz
φ’’(t) + ω02φ(t) = 0
20

21.

Физический маятник/. Приведенная длина
o
L0C
C
m
Физический маятник - массивное тело, совершающее
(небольшие) колебания относительно оси подвеса
с круговой частотой ω02 = mgL0C/Iz
Математический маятник – материальная точка на
невесомом подвесе длины L, совершающая (небольшие)
колебания с круговой частотой ω02 = g/L
Приведенная длина Lпривед физического маятника равна длине
математического маятника, совершающего колебания с такой-же частотой:
ω02 = mgL0C/Iz = g/L привед => Lпривед = Iz /mL0C
21

22.

Условия равновесия для твердого тела
o
L
C
m
Колебания физического маятника у положения равновесия –
= частный случай вращательного движения.
φ(t) = φ0 cos(ω0t+a), где требуют уточнения константы
φ0 – амплитуда колебаний, и a - начальная фаза колебаний
Круговая частота колебаний ω02 = mgL/Iz
Уточним определение равновесия для твердого тела и его условия (их 2):.
равенство нулю суммы сил, действующих на тело: ΣF = 0
равенство нулю суммы моментов сил, действующих на тело: ΣN = 0
ВАЖНО! dM/dt = ΣN . Если ΣN = 0 => М = Izω = Const => ω = Const
:Вращение с постоянной угловой скоростью = состояние равновесного движения
твердого тела. В отсутствие внешних сил оно может продолжаться неограниченно
долго (вращение Земли, например) Но! Это не состояние покоя, каковым является
только движение с постоянной поступательной скоростью относительно ИСО.
1.
2.
NB: положения устойчивого равновесия, вблизи которых возможны
колебания = точки минимумов потенциальной энергии системы
22

23.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Далее:
Механика больших скоростей
(релятивистская механика)..