Similar presentations:
6. Вычисление пределов
1. Вычисление предела функции
12.
2 x 5 3x 3 1Пример 1. Вычислить lim 5
2
x x 4 x 2 x
Решение. Делим числитель и знаменатель
дроби почленно на наивысшую из имеющихся
степень переменной x, т.е. на x5.
2 x 5 3x 3
1
3
1
2
x 2 x5
x5
x5
x5
2 x 5 3x 3 1
lim
lim 5
2
4
2
lim
5
2
x
x
4x
2x
x
1
x x 4 x 2 x
3
4
5 5
5
x
x
x
x
x
3
1
3
1
2 lim 2 lim 5 2 0 0 2
2 2 5 lim
lim
x
x x
x x
x
x
x
2
4
2
4
2
1 0 0 1
1
lim
1
lim
lim
lim
2
x x 3
x x 4
x 3 x 4 x
x
3.
Пример 2. Вычислить5x3 x 2 1
lim
4
2
x 2 x 3 x 5 x 2
Решение. Делим числитель и знаменатель
дроби почленно на наивысшую из имеющихся
степень переменной x т.е. на x4.
5
1
1
5x3 x 2
1
x x2 x4
x4
x4 x4
5x3 x 2 1
lim
4
2
lim
3
5
2
lim
4
2
3x
5x
2
x
x 2 x
2 2 3 4
x 2 x 3 x 5 x 2
4
4
4
4
x
x
x
x
x
x
x
5
1
1
1
1
5
lim
lim
lim
2 4
lim
x x
x x 2
x x 4
x
x
x x
3
5
2
3
5
2
2 2 3 4 lim 2 lim
lim
lim
lim
x
x
x x
x
x x 2
x x 3
x x 4
0 0 0
0
0
2 0 0 0 2
3
4.
2x6 x2 14
3
Пример 3. Вычислить lim
x
2
x
x
x
Решение. Делим числитель и знаменатель
дроби почленно на наивысшую из имеющихся
степень переменной x, т.е. на x6.
1
1
2x6 x2
1
2 4 6
6 6
6
6
2
x
x
x
x
x
2x x 1
lim
lim x 4 2 x 3
1
2
1
lim
4
3
x
x
x
x
2
x
x
3 5
x
6 6
2
6
x
x
x
x
x
x
1
1
1
1
lim 2 lim 4 lim 6
2 4 6
lim
x
x x
x x
x
x
n
1
2
1
2
1
1
2 3 5 lim 2 lim 3 lim 5
lim
x x
x x
x
x x x
n x
2 0 0 2
(не существует)
0 0 0 0
4
5. Правила вычисления пределов
ПРАВИЛА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ1. Если старшая степень
числителя и знаменателя
совпадают, то предел такого вида
всегда будет равен отношению
коэффициентов при старших
степенях переменной.
2 x 3x 1
- старшая степень
2
lim
5
2
x x 4 x 2 x
5
3
числителя и знаменателя совпадают
5
6. Правила вычисления пределов
ПРАВИЛА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ2. Если степень знаменателя
выше степени числителя, то
предел такого вида равен
нулю.
5x x 1
- старшая
0
lim
4
2
x 2 x 3 x 5 x 2
3
2
степень знаменателя выше степени числителя
6
7. Правила вычисления пределов
ПРАВИЛА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ3. Если же старшая степень числителя выше
степени знаменателя, то, очевидно, все
слагаемые знаменателя в пределе будут равны
нулю, это означает, что предел не существует.
x x 1
- старшая степень
lim
4
3
x x 2 x x
6
2
числителя выше степени знаменателя
7
8.
Вычислите самостоятельно пределы функций набесконечности:
x4 4x 2
1. lim 2
x 5 x 3 x 1
3x
2. lim x 2 3x 7 0
x
x 4x 7
3. lim 2
x x 4 x 3
4
2
6 x 3 3x 2 x 1 6
3
4. lim
3
2 x x 13
x
2
8
9. Методика вычисления пределов в точке
МЕТОДИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ВТОЧКЕ
Если функция существует в точке x = a, то ее
предел равен f(a).
Пример 1. Вычислить lim (2 x 5)
x 3
Решение. Подставим вместо x число 3 (т.к. x 3) и
применим правила вычисления пределов.
(2 x 5) lim 2 x lim 5 2 lim x lim 5
lim
x 3
x 3
x 3
x 3
x 3
6 5 2 3 5 11
9
10.
lim ( x 2 x 3)2
Пример 2. Вычислить
Решение.
x ( 2 )
lim ( x 2 x 3) lim x lim 2 x lim 3
2
2
x ( 2 )
x ( 2 )
x ( 2 )
x ( 2 )
lim x 2 lim x lim 3
2
x ( 2 )
x ( 2 )
x ( 2 )
( 2) 2 ( 2) 3 4 4 3 3
3x
Пример 3. Вычислить lim 2 x 1
x 3
Решение.
3 lim x
2
lim 3 x
x 3
3x
x 3
lim
2 lim x lim1
lim( 2 x 1)
x 3 2 x 1
x 3
x 3
x 3
3 3
1,8
2 3 1
10
11.
x3Пример 4. Вычислить lim 3
x 2 x x 2 4
Решение. Подставим вместо x число 2 (т.к. x 2) и
применим правила вычисления пределов.
lim x 3
3
x
x 2
lim 3
3
2
2
x 2 x x 4
lim( x x 4)
lim x
3
x 2
3
2
3
3
2
2
lim x lim x lim 4 2 2 4
x 2
x 2
x 2
x 2
8
8
8 4 4 0
11
12.
МЕТОДИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ВТОЧКЕ
0
Правило раскрытия неопределенности . 0
0
Чтобы раскрыть неопределенность
0 ,
нужно числитель и знаменатель дроби разложить на
множители так, чтобы можно было сократить.
14
13.
x2 4x 5Пример 1. Вычислить lim 2
x 1 x 4 x 3
Используемые формулы:
Разложение квадратного трехчлена на множители
ax2+bx+c=a(x-x1)(x-x2),
где х1, х2 корни квадратного уравнения ax2+bx+c=0.
( x 1)( x 5)
x2 4x 5 0
lim
lim
2
x 1 x 4 x 3
0 x 1 ( x 1)( x 3)
( x 5)
6
lim
3
x 1 ( x 3)
2
15
14. Методика вычисления пределов в точке
x 2 9 x 14Пример 2. Вычислить lim 2
x 2 x 3 x 10
Используемые формулы:
Разложение квадратного трехчлена на множители
ax2+bx+c=a(x-x1)(x-x2),
где х1, х2 корни квадратного уравнения ax2+bx+c=0.
( x 2)( x 7)
x 2 9 x 14 0
lim
lim
2
x 2 x 3 x 10
0 x 2 ( x 2)( x 5)
5
( x 7)
lim
x 2 ( x 5)
7
16
15.
Активно используйте формулы сокращенногоумножения
x2 4
3
Пример 3. Вычислить lim
x 2 x 8
Решение. Выяснили, что при х = 2 и числитель и
знаменатель равны нулю, значит имеем неопределенность









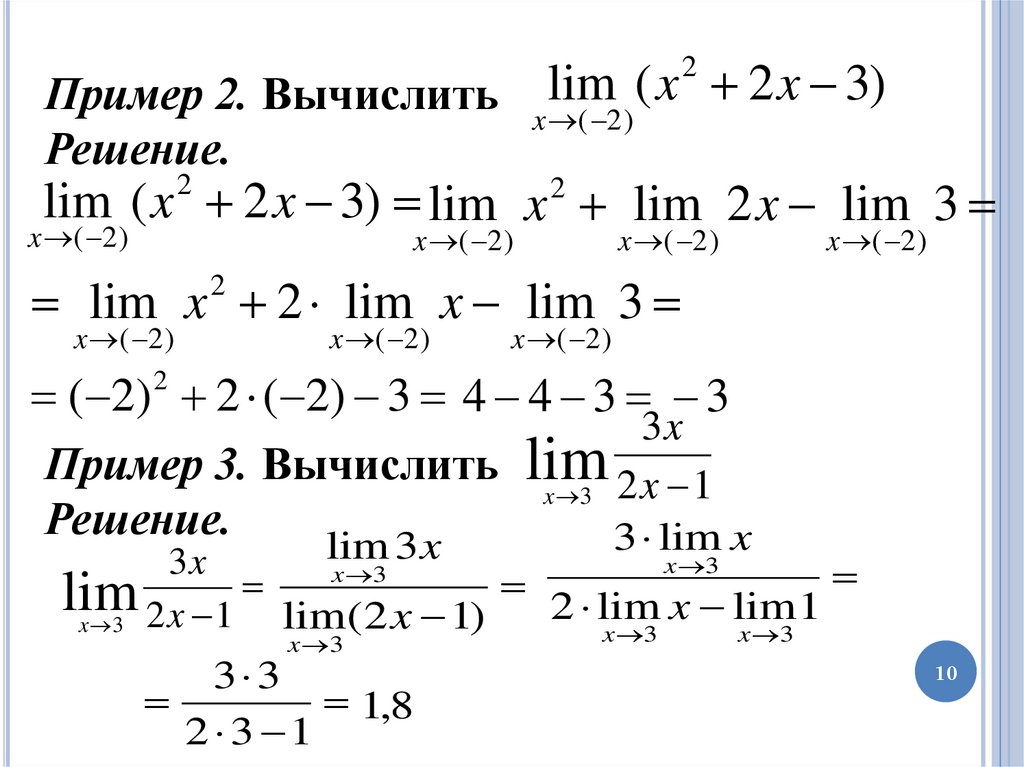







 mathematics
mathematics