Элементы квантовой механики

1.

Тема лекции:
Элементы квантовой механики
Вопросы:
1. Волна де Бройля.
2. Соотношение неопределенностей.
3. Волновая функция.
4. Уравнение Шредингера.
5. Движение свободной частицы.
6. Частица в потенциальной яме с бесконечно высокими
«стенками».
7. Гармонический осциллятор.
8. Прохождение частиц сквозь потенциальный барьер.
Туннельный эффект.
9. Квантовая частица в сферически симметричном
поле.

2.

Луи де Бройль высказал предположение, что
двойственность свойств присуща не только
фотонам (квантам электромагнитного излучения), но и любым частицам вещества.
Причем количественные соотношения между волновыми и квантовыми свойствами частиц такие же, как
и для фотонов:
h
p
и
h
.
Подтверждением гипотезы де Бройля явился опыт
по дифракции электронов на кристалле никеля.
Луи де Бройль
Лауреат Нобелевской
премии по физике
1892 - 1987
Впоследствии опыты были проведены с нейтронами, протонами, атомами и молекулами. Всюду гипотеза де Бройля блестяще подтвердилась.
Присущи ли волновые свойства макрообъектам?
Считают, что макрообъекты проявляют только корпускулярные свойства, а волновые свойства выражены
крайне слабо.
2

3.

Сравним дифракцию световых волн и микрочастиц.
При дифракции световых волн происходит перераспределение энергии волны, в
результате на экране наблюдаются участки различной интенсивности. С точки зрения
квантовой теории интенсивность света больше там, куда больше попало фотонов, т.е. где
больше вероятность попадания фотонов. Можно сделать вывод, что интенсивность
световой волны в разных точках экрана пропорциональна вероятности
попадания фотона в эту точку пространства.
Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется
неодинаковым распределением числа частиц по разным направлениям. Можно
утверждать, что вероятность попадания микрочастицы в ту или другую точку
пространства пропорциональна интенсивности волн де Бройля.
Вероятностный подход к описанию микрочастиц – важнейшая
особенность квантовой теории.
3

4.

Двойственная корпускулярно-волновая природа частиц вещества ставит вопрос о
границах применимости классической физики: до каких пор можно пользоваться
классическими представлениями и учитывать только корпускулярные свойства тел?
Вернер Гейзенберг пришел (1927 г.) к выводу, что
объект микромира нельзя одновременно с любой высокой
точностью характеризовать его координатой и импульсом:
произведение неопределенностей координат
на соответствующие неопределенности
импульса не может быть меньше постоянной
Планка h
x p x h
y p y h
z p z h
Это соотношение необходимо для понимания многих
особенностей микромира.
Вернер Гейзенберг
1901–1976
4

5.

Соотношение неопределённостей приводит к важному следствию:
микрочастицы не могут покоиться! Поэтому:
в атомах и молекулах при температуре 0 К сохраняется движение электронов
около ядра и ядер относительно друг друга (нулевые колебания);
чем меньше область пространства, в которой находится частица, тем большая
энергия требуется для ее удержания.
Соотношение неопределённостей для энергии и времени:
E t h
т.е. разброс значений энергии Е возрастает с уменьшением среднего времени
жизни t частицы.
Например, по ширине спектральной линии можно оценить время нахождения атома в
возбужденном состоянии.
Существенно, что невозможность одновременно точного определения
координат и импульса или энергии и времени не есть следствие
несовершенства измерительной техники. Это принципиальная
невозможность, отражающая двойственную природу микрочастиц.
5

6.

Для описания движущихся микрочастиц в квантовой теории разработан некий
математический формализм, суть которого в следующем.
Каждой микрочастице ставится в соответствие некоторая функция, значение
которой зависит от координат и времени (x , y, z ,t ) - это так называемая псифункция.
Формально пси-функция обладает свойством классической волны, поэтому
ее часто называют волновой функцией.
Волновая функция является основным носителем информации о волновых и
квантовых свойствах частиц и полностью описывает их состояние.
Квадрат модуля волновой функции (x , y, z ,t ) пропорционален вероятности
обнаружить частицу в момент времени t в элементе объема dV dx dy dz :
2
dw dV .
2
Величина определяет интенсивность волн де Бройля.
2
6

7.

.
Вероятность обнаружить частицу в момент времени t в конечном объеме V
w dw dV .
2
V
V
Пси-функция удовлетворяет условию нормировки
2
dV 1,
т.е. обнаружить частицу где-нибудь в бесконечном объеме есть достоверное
событие.
Пси-функция является объективной характеристикой состояния
микрочастицы, поэтому она конечна (w 1), однозначна и непрерывна.
7

8.

.
– это уравнение движения микрочастиц в силовых полях:
2 2
U (x , y, z , t ) i
2m
t
h
;
2
m - масса частицы;
2
2
2
2 2 2 - оператор Лапласа;
x
y
z
i 1 - мнимая единица;
U (x , y, z , t ) - потенциальная энергия частицы
2
в силовом поле, в котором она движется;
(x , y, z , t ) - искомая волновая функция.
Эрвин Шрёдингер
1887 - 1961
8

9.

Уравнение Шредингера в квантовой механике играет такую же
роль, что и уравнение Ньютона в классической механике. Как и другие
фундаментальные законы физики, оно не выводится, а постулируется.
Правильность его подтверждается опытом, что и придает ему статус
закона природы.
Если силовое поле стационарно, т.е. не зависит от времени, то U (x , y, z )
имеет смысл потенциальной энергии, и решение уравнения Шрёдингера можно
представить в виде произведения двух функций: только координат и только
времени
(x , y , z ) e
i
E
t
,
где E WK WP – полная энергия частицы, не зависящая от времени. В этом
случае имеет место стационарное уравнение Шрёдингера
2m
2 (E U ) 0 .
2
Разность (E U ) является кинетической энергией частицы.
9

10.

Частица называется свободной, если на нее ничто не действует. В этом
случае потенциальная энергия частицы U = 0, а ее полная энергия равна
кинетической энергии.
Пусть частица движется вдоль оси Х, тогда уравнение Шредингера
2 2mE
2 0.
2
x
Решением данного уравнения является плоская монохроматическая волна
Ae i ( t kx ) ,
где волновое число k
Так как k
2
, то
h
p
2mE mv p
p k .
– это волна де Бройля.
Таким образом, свободная частица в квантовой механике описывается
плоской монохроматической волной де Бройля. Этому соответствует не
зависящая от времени вероятность обнаружить частицу в данной точке
2
пространства, причем одинаковая в любой точке * A .
2

11.

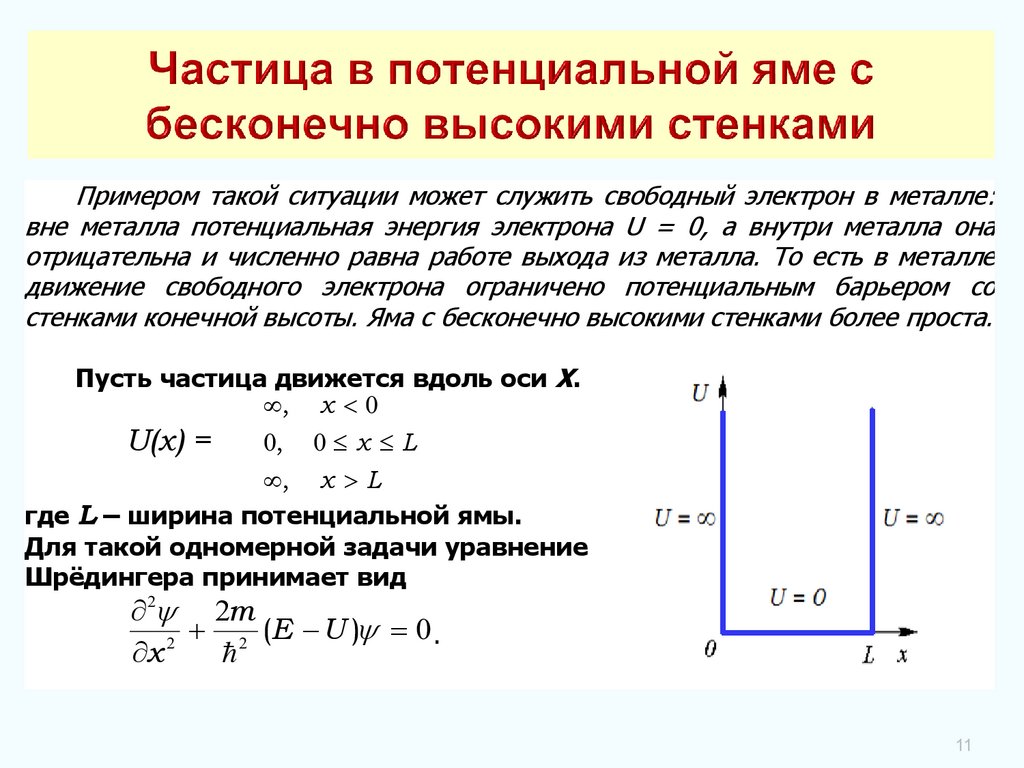
Примером такой ситуации может служить свободный электрон в металле:
вне металла потенциальная энергия электрона U = 0, а внутри металла она
отрицательна и численно равна работе выхода из металла. То есть в металле
движение свободного электрона ограничено потенциальным барьером со
стенками конечной высоты. Яма с бесконечно высокими стенками более проста.
Пусть частица движется вдоль оси Х.
, x 0
0, 0 x L
U(x) =
, x L
где L – ширина потенциальной ямы.
Для такой одномерной задачи уравнение
Шрёдингера принимает вид
2 2m
2 (E U ) 0 .
2
x
11

12.

Так как высота стенок бесконечна, то вероятность обнаружить частицу
за пределами ямы рана нулю, т.е. 0 .
В силу непрерывности волновой функции граничные условия
(0) 0; (L ) 0 .
В пределах ямы (0 < x < L) уравнение Шредингера
2 2m
2
2
или
E
0
k
0,
2
2
2
x
x
2m
где
(*)
k2 2 E .
Общее решение этого дифференциального уравнения
(x ) A sin kx B cos kx .
По первому граничному условию (0) = 0, поэтому В = 0.
Из второго граничного условия (L) = 0, то есть
(L ) A sin kL 0 .
Это возможно, если kL = nπ, где n = 1, 2, ... . Из выражения (*) следует, что
n 2 2 2
En
2mL2
12

13.

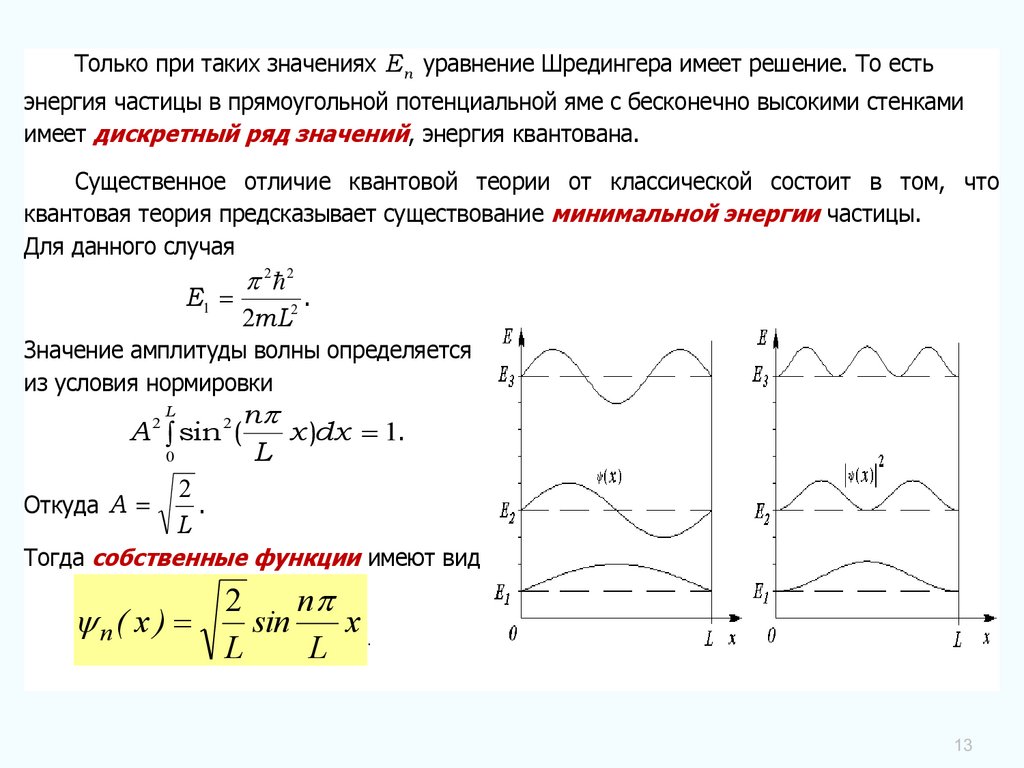
Только при таких значениях En уравнение Шредингера имеет решение. То есть
энергия частицы в прямоугольной потенциальной яме с бесконечно высокими стенками
имеет дискретный ряд значений, энергия квантована.
Существенное отличие квантовой теории от классической состоит в том, что
квантовая теория предсказывает существование минимальной энергии частицы.
Для данного случая
2 2
E1
.
2
2mL
Значение амплитуды волны определяется
из условия нормировки
n
A sin 2 (
x )dx 1.
L
0
2
Откуда A
.
L
2
L
Тогда собственные функции имеют вид
2
n
n( x )
sin
x.
L
L
13

14.

Гармонический осциллятор
Гармоническим осциллятором называют
частицу, совершающую одномерное движение
под действием квазиупругой силы F = - kx.
Потенциальная энергия частицы
U kx / 2
2
или
m 2 x 2
U
,
2
где k
m

15.

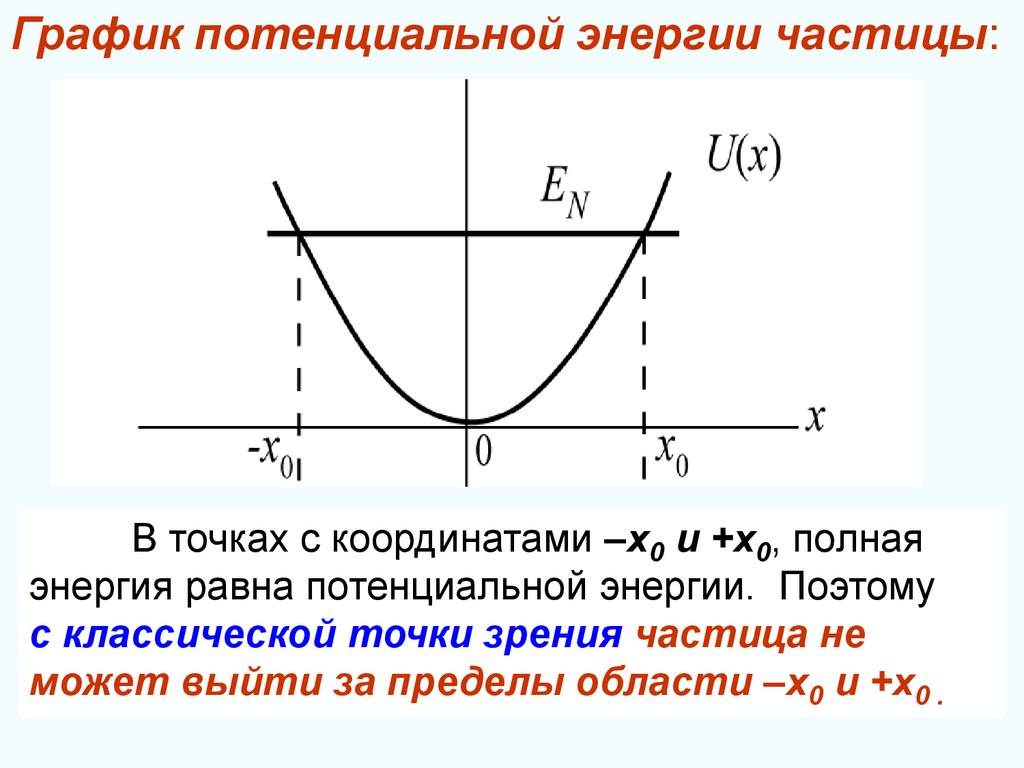
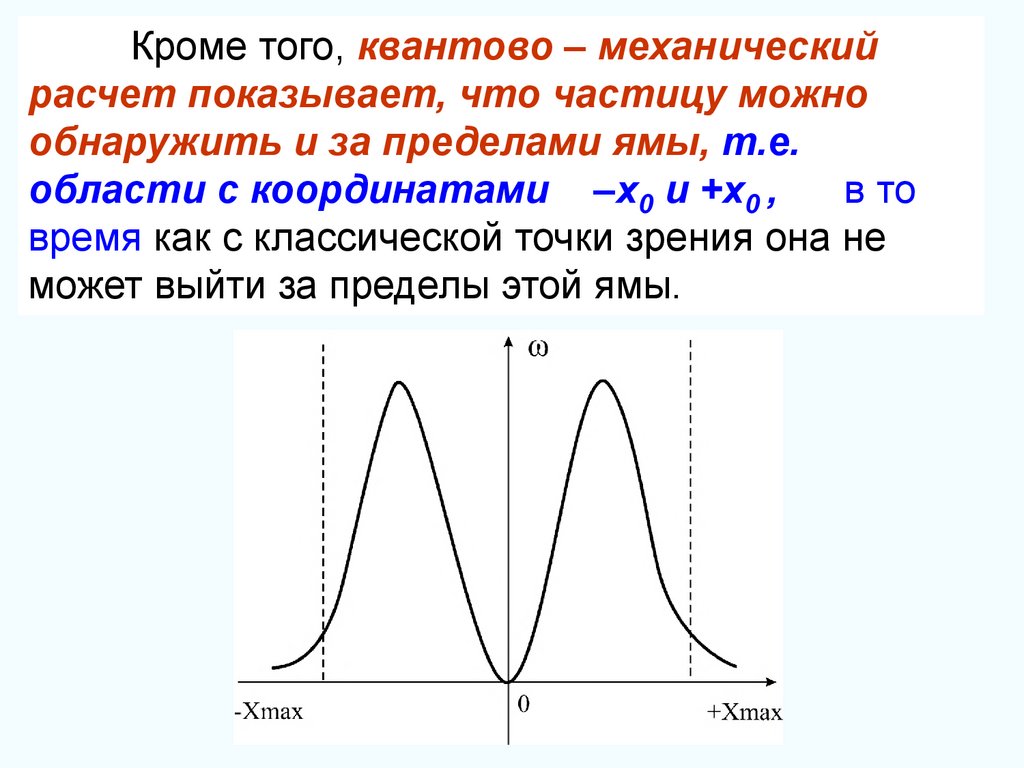
График потенциальной энергии частицы:
.
В точках с координатами –x0 и +x0, полная
энергия равна потенциальной энергии. Поэтому
с классической точки зрения частица не
может выйти за пределы области –x0 и +x0 .

16.

Гармонический осциллятор в квантовой
механике - квантовый осциллятор описывается уравнением Шредингера:
d Ψ 2m
m x
2 (E
)Ψ 0
2
2
dx
2
2
2
Значения полной энергии
осциллятора
En (n 1 / 2) , где n = 0, 1, 2…

17.

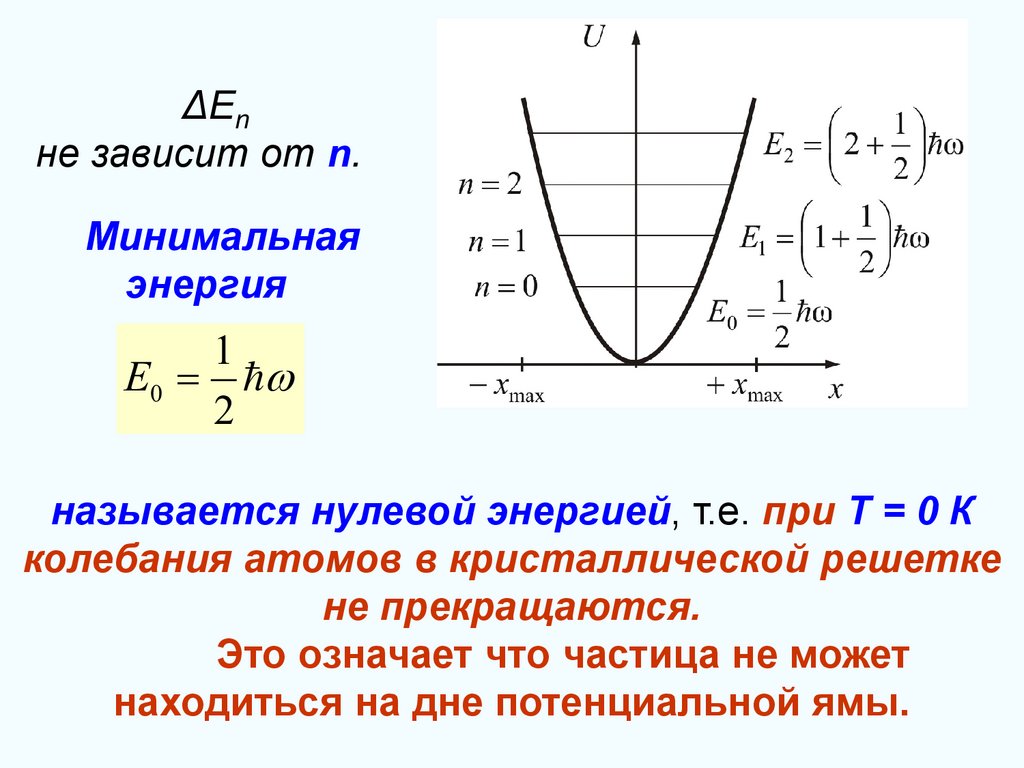
ΔEn
не зависит от n.
Минимальная
энергия
1
E0
2
называется нулевой энергией, т.е. при Т = 0 К
колебания атомов в кристаллической решетке
не прекращаются.
Это означает что частица не может
находиться на дне потенциальной ямы.

18.

В
квантовой
механике
вычисляется
вероятность различных переходов квантовой
системы из одного состояния в другое. Для
гармонического осциллятора возможны лишь
переходы между соседними уровнями.
Условия, накладываемые на
изменения квантовых чисел при
переходах системы из одного
состояния в другое, называются
правилами отбора
n 1

19.

Таким образом, энергия
гармонического осциллятора
изменяется только порциями
E n , т.е. квантуется.
1
Причем минимальная энергия E0
2

20.

Кроме того, квантово – механический
расчет показывает, что частицу можно
обнаружить и за пределами ямы, т.е.
в то
области с координатами –x0 и +x0 ,
время как с классической точки зрения она не
может выйти за пределы этой ямы.

21.

Прохождение частиц сквозь
потенциальный барьер. Туннельный эффект
Рассмотрим простейший потенциальный
барьер прямоугольной формы высоты U
и шириной l для одномерного (по оси х)
движения частицы.
Рисунок 5
1 обл.
0, x 0
U ( x) U , 0 x 1 2 обл.
0, x 1
3 обл.
При данных условиях задачи классическая частица,
обладая энергией Е:
либо беспрепятственно пройдет под барьером (E > U) ,
либо отразится от него (E < U) и будет двигаться в
обратную сторону, т.е. она не может проникнуть через барьер.

22.

Для микрочастицы
даже при E > U, имеется
отличная от нуля
возможность, что
частица отразится от
барьера и будет
двигаться в обратную
сторону.
А при E < U имеется отличная от нуля
вероятность, что частица окажется в
области x > l, т.е. проникнет сквозь барьер.
Такой вывод следует непосредственно из решения
уравнения
Шредингера,
описывающего
движение
микрочастицы при данных условиях задачи.

23.

Уравнение Шредингера для состояний в каждой из
выделенных областей имеет вид:
1,3
2
x 2
2mE
2
k 1,3 0 для1, 3 обл. k 2
2
2
2
q 2 0
2
x
2
2 m( E U )
2
для 2 обл. q
2
2m(U E )
Здесь q = iβ – мнимое число, β
.
Общее решение этих дифференциальных уравнений:
Ψ1( x ) A1eikx B1e ikx ( 1 )
Ψ 2 ( x ) A2eiqx B2e iqx ( 2 )
ikx
ikx
Ψ3( x ) A3e B3e
(3)

24.

Учитывая значение q и то, что А1 = 1, B3 = 0, получим
решение уравнения Шредингера для трех областей в
следующем виде:
Ψ1( x ) A1e
ikx
Ψ 2 ( x ) A2e
Ψ3( x ) A3e
B1e
x
ikx
ikx
x
B2e
(1 )
(2)
(3)
В области 2 функция уже не соответствует
плоским волнам, распространяющимся в обе
стороны, поскольку показатели степени не
мнимые а действительные.

25.

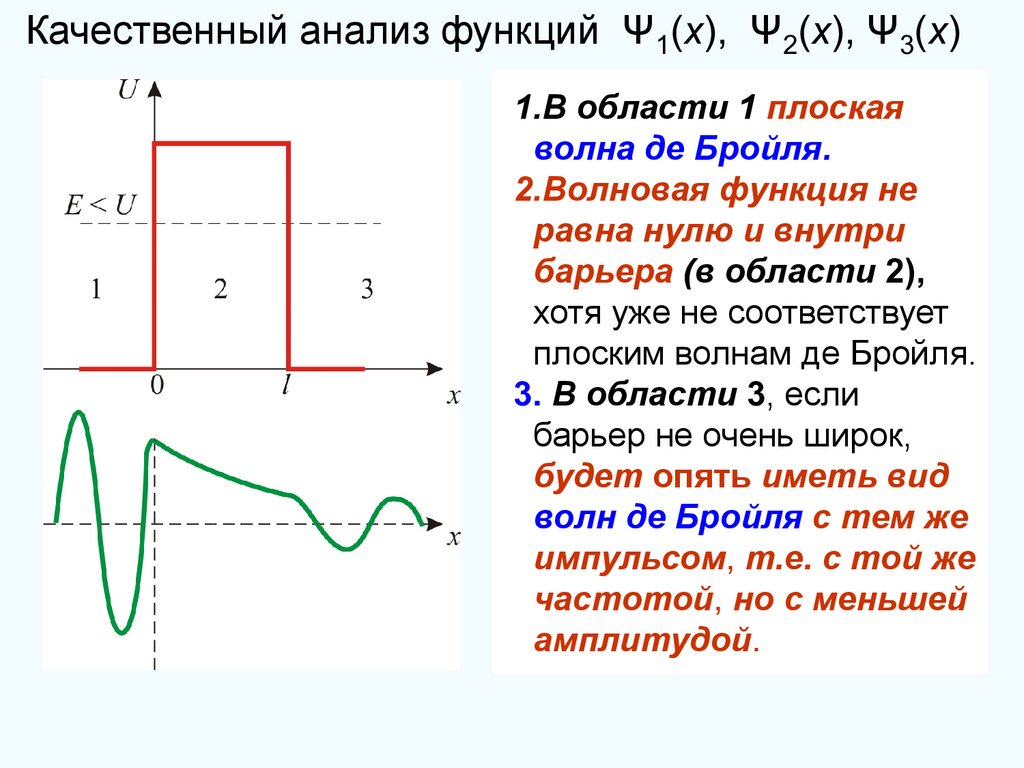
Качественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x)
1.В области 1 плоская
волна де Бройля.
2.Волновая функция не
равна нулю и внутри
барьера (в области 2),
хотя уже не соответствует
плоским волнам де Бройля.
3. В области 3, если
барьер не очень широк,
будет опять иметь вид
волн де Бройля с тем же
импульсом, т.е. с той же
частотой, но с меньшей
амплитудой.

26.

Таким образом, квантовая
механика приводит к
принципиально новому
квантовому явлению туннельному эффекту,
в результате которого
микрообъект может пройти
через барьер.

27.

Коэффициент прозрачности для
барьера прямоугольной формы
2
D D0exp
2m(U E )l
Для барьера произвольной формы
2 x2
D D0exp 2m(U E )l dx
x
1

28.

Прохождение частицы сквозь ,барьер можно
пояснить соотношением неопределенностей:
Неопределенность импульса на отрезке Δx=l
составляет х p .
Связанная с разбросом в значении импульса
p
кинетическая энергия Е
2m
2
p
l
может оказаться достаточной для того,
чтобы полная энергия оказалась больше
высоты потенциального барьера..

29.

С классической точки зрения
прохождение частицы сквозь
потенциальный барьер при E < U
невозможно, так как частица, находясь в
области барьера, должна была бы обладать
отрицательной кинетической энергией.
Туннельный эффект является
специфическим квантовым эффектом.

30.

Основы теории туннельных переходов
заложены работами советских ученых
Л.И. Мандельштама и М.А. Леонтовича
в 1928 г.
Туннельное прохождение сквозь
потенциальный барьер лежит в основе
многих явлений:
• физики твердого тела (например, явления
в контактном слое на границе двух
полупроводников),
• атомной и ядерной физики
(например, α-распад, протекание
термоядерных реакций).

31.

Решение этой задачи позволяет описать состоянии электрона в атоме водорода
и в водородоподобных системах (Hе+, Li++ ...).
Потенциальная энергия взаимодействия электрона с ядром
Ze 2
U (r )
,
4 0r
r – расстояние между электроном и ядром;
Ze – заряд ядра (для водорода Z = 1).
Уравнение Шредингера в данном случае
2m
Ze 2
2 (E
) 0 .
4 0r
2
Уравнение имеет решение, если значения энергии
Z 2me 4
En 2 2 2 , где n = 1, 2, ...
8n h 0
Уровень E 1 , соответствующий минимальной энергии,
называется основным ; остальные – возбужденными.
Пока Е < 0, электрон находится в гиперболической
потенциальной яме и является связанным.
При Е > 0 электрон становится свободным, и он может
уйти в бесконечность. В таком состоянии электрон имеет
непрерывный спектр энергии.
Энергия ионизации Ei E1 .

32.

Поглощая энергию извне, электрон переходит в возбуждённое состояние, которому
соответствует большее значение энергии. Возвращаясь в стационарное состояние,
электрон излучает квант, энергия которого равна разности энергий возбужденного Em и
стационарного En состояний:
hc
h mn
Em En Emn .
mn
Каждый атом характеризуется определенным набором уровней разрешенной
энергии.
В зависимости от случайных обстоятельств возникают самые различные
энергетические переходы.
32

33.

Переходя после возбуждения на нижележащий уровень, электрон излучает квант, энергию
которого для атома водорода можно рассчитать по формуле
c
1
1
hcR 2 2 ,
mn
m
n
где m определяет номер уровня, с которого электрон переходит, n – на который;
h mn h
-1
R 1,097 107 м
- постоянная Ридберга.
Такие переходы могут происходить «прыжками» через различное число
ступеней. Поэтому спектр излучения состоит из набора некоторого числа
линий – это линейчатый спектр излучения.
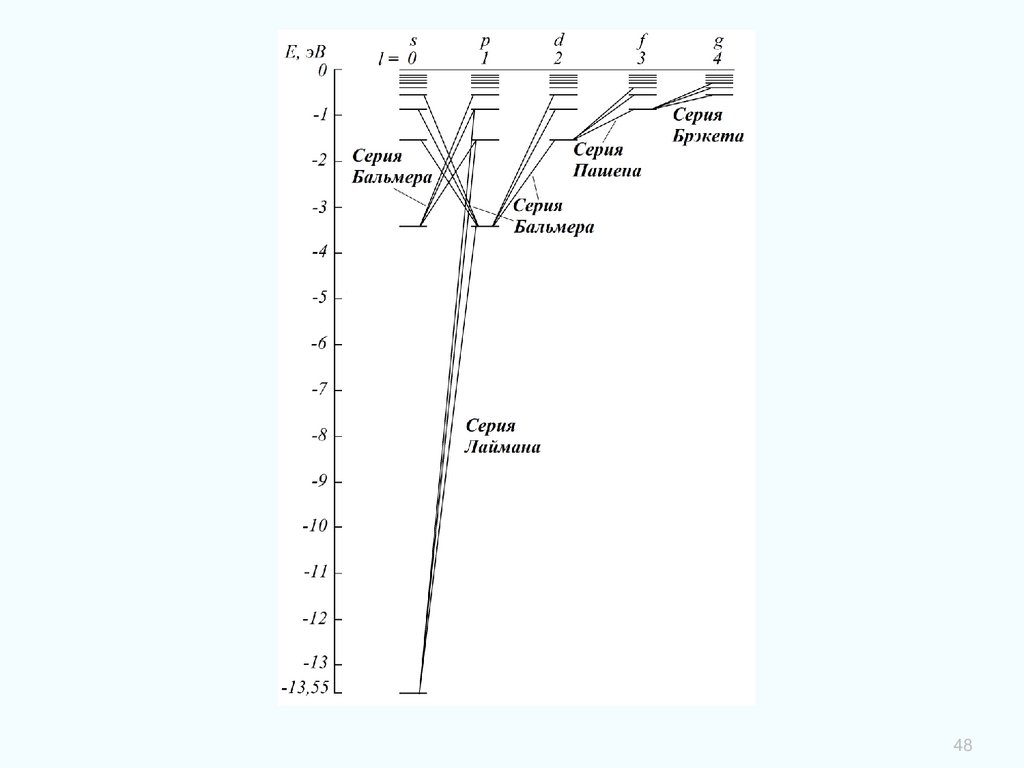
В зависимости от значения числа n различают спектральные серии:
серия Лаймана (n = 1; m = 2, 3, 4, …),
серия Бальмера (n = 2; m = 3, 4, 5, …),
серия Пашена (n = 3; m = 4, 5, 6, …),
серия Пфунда (n = 4; m = 5, 6, 7, …) ...
Первые четыре линии серии Бальмера лежат в видимой области спектра.
33

34.

Уравнению Шредингера удовлетворяют собственные функции nlm (r , , ), которые определяются
тремя квантовыми числами: n, l и m.
Главное квантовое число n определяет энергию электрона в атоме, и оно может принимать
значения
n = 1, 2, ... .
Момент импульса электрона в атоме может принимать только определенные дискретные значения
Ll l (l 1) .
Орбитальное квантовое число l определяет момент импульса электрона в атоме, которое при
заданном n может принимать значения
l = 0, 1, ... , (n – 1).
Проекция вектора момента импульса электрона на направление внешнего магнитного поля B также
может принимать только дискретные значения, кратные :
L l B m .
Магнитное квантовое число m определяет проекцию момента импульса электрона на заданное
направление внешнего магнитного поля, которое при заданном l может принимать значения
m = –l, – (l – 1), ... , – 1, ... , (l – 1), l.
Каждому собственному значению En (кроме E1 ) соответствует несколько собственных функций
nlm , отличающихся значениями l и m. Т.е. атом может иметь одно значение энергии, но находиться в
нескольких различных состояниях. Это явление называется вырождением. Степень вырождения равна
n 1
(2l 1) n .
l 0
2
34

35.

Орбитальное квантовое число
l = 0, 1, 2,...n – 1
определяет момент импульса электрона L.
Состояния, соответствующие орбитальному числу
l = 0, 1, 2, 3,…, обозначаются буквами
s, p, d, f,….
sharp, principal, diffuse, fundamental
0
1
2
3
s
p
d
f
l

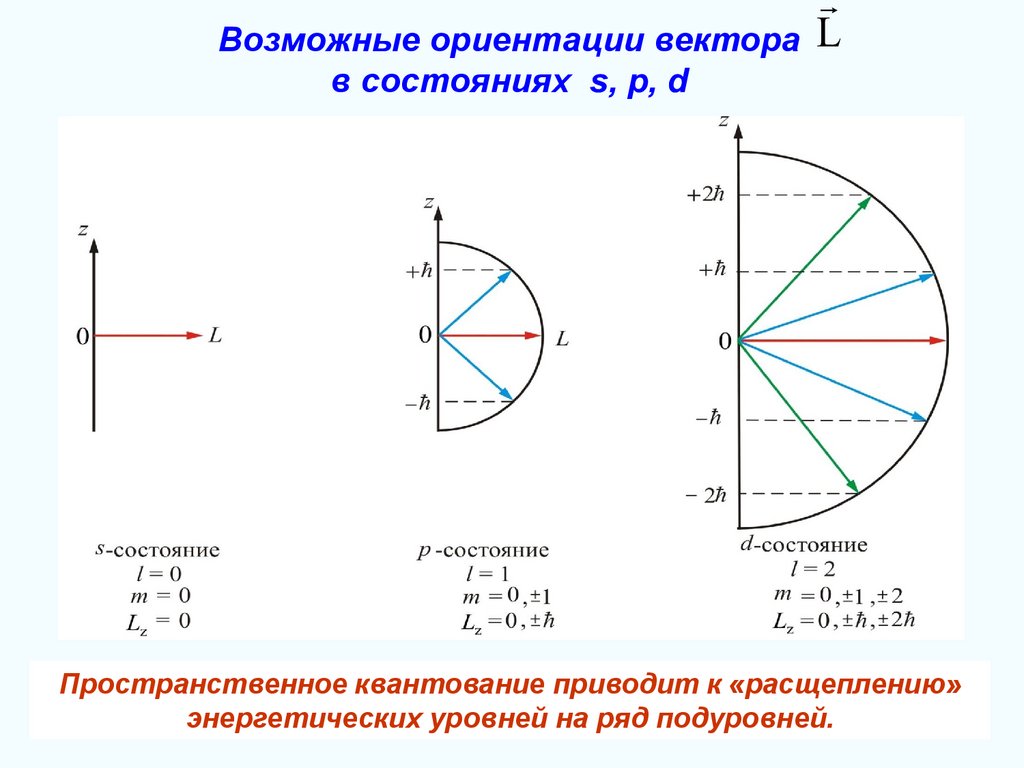
36.

Возможные ориентации вектора L
в состояниях s, p, d
Пространственное квантование приводит к «расщеплению»
энергетических уровней на ряд подуровней.

37.

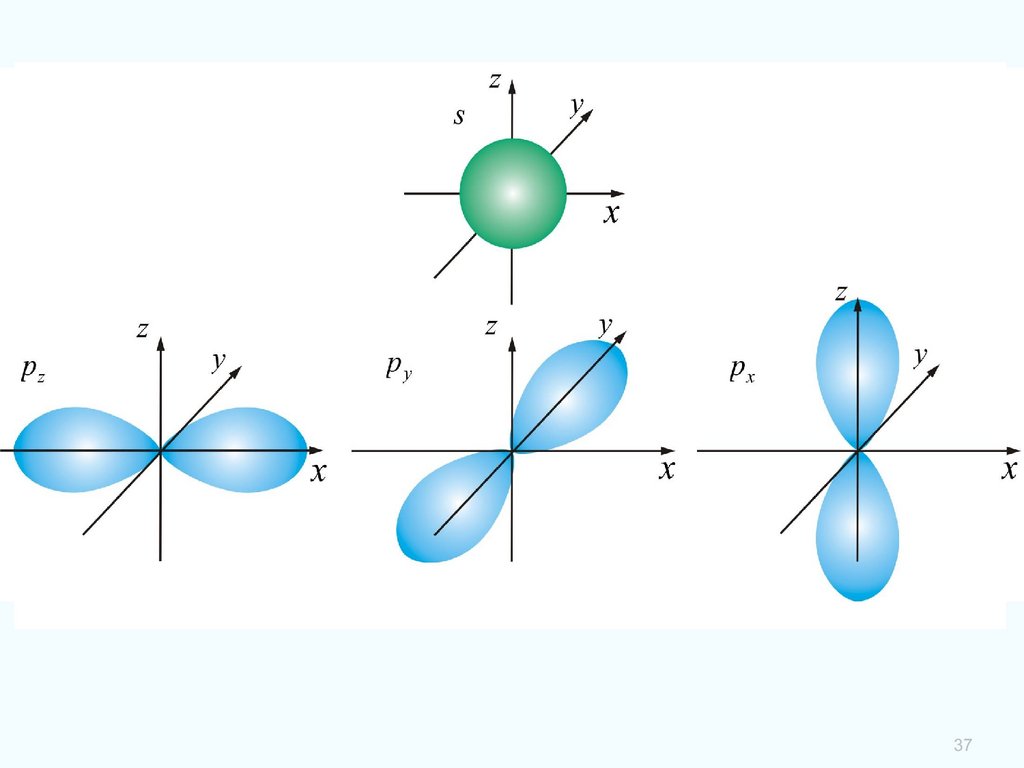
Квадрат модуля волновой функции определяет вероятность обнаружить электрон в
единице объема. Электрон при своем движении в атоме образует электронное облако,
плотность которого характеризует вероятность нахождения электрона в различных точках
объема атома. Квантовые числа n и l определяют размер и форму электронного облака, а m –
ориентацию облака в пространстве.
2
Электрон, кроме того, обладает собственным моментом импульса, не связанным с его
движением в пространстве – спином. Спин электрона квантуется по закону LS mS , где
mS - магнитное спиновое квантовое число, которое может принимать только два
значения:
1
mS .
2
Для полного описания состояния электрона в атоме необходимо задать четыре квантовые
числа: n, l, m, mS.
Распределение электронов в атоме подчиняется принципу Паули: в одном атоме не
может быть более одного электрона с одинаковым набором квантовых чисел n, l, m, mS. Два
электрона, связанные в одном атоме, различаются значением, по крайней мере, одного
37
квантового числа.

38.

Опыт Штерна и Герлаха
В 1922 году Штерн и Герлах
поставили опыты, целью которых было
измерение магнитных моментов атомов
различных химических элементов.
Для химических элементов, образующих
первую группу таблицы Менделеева и
имеющих
один
валентный
электрон,
магнитный момент атома равен магнитному
моменту одного валентного электрона.

39.

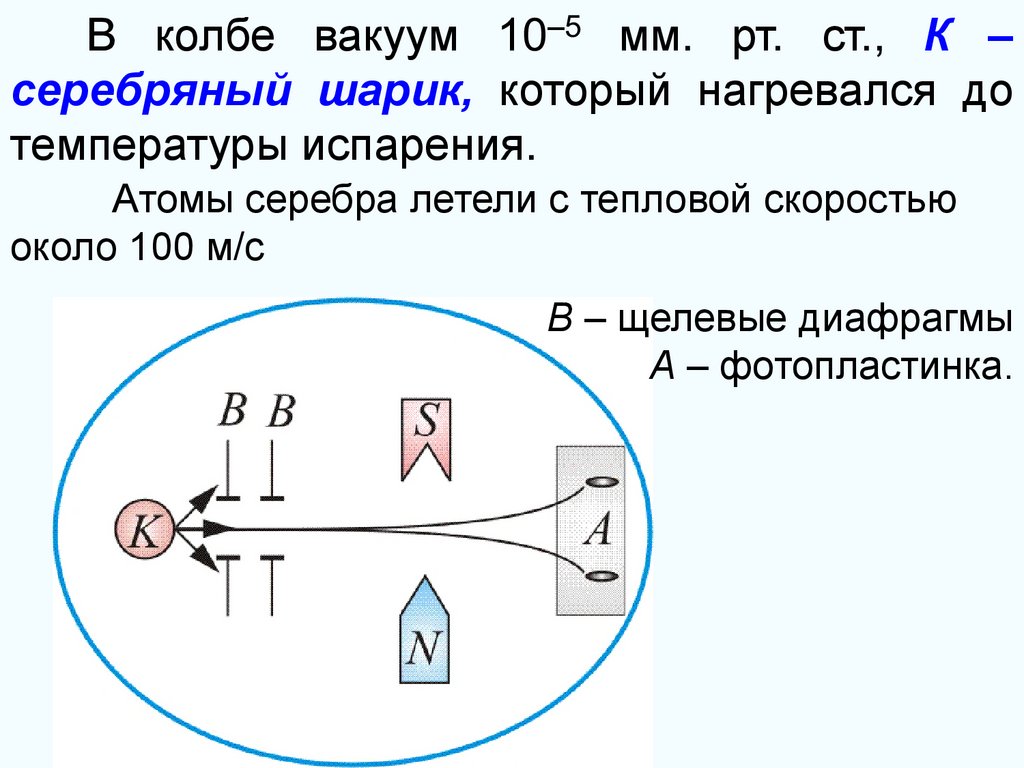
В колбе вакуум 10–5 мм. рт. ст., К –
серебряный шарик, который нагревался до
температуры испарения.
Атомы серебра летели с тепловой скоростью
около 100 м/с
В – щелевые диафрагмы
А – фотопластинка.
Рисунок 5

40.

Если бы момент импульса L мог принимать
произвольные ориентации в пространстве, т.е.
в магнитном поле, то можно было ожидать
непрерывного
распределения
попаданий
атомов серебра на фотопластинку с большой
плотностью попаданий в середине.
Но на опыте были получены совершенно
неожиданные результаты: на фотопластинке
получились две резкие полосы – все атомы
отклонялись в магнитном поле двояким
образом,
соответствующим
лишь
двум
возможным ориентациям магнитного
момента.

41.

Этим доказывался квантовый характер
магнитных моментов электронов.
Количественный анализ показал, что
проекция магнитного момента электрона
равна
e
0,927 10 23 –Дж Тл 1 магнетон
Б
2m
Бора
Т.е. для серебра Штерн и Герлах
получили,
что
проекция
магнитного
момента атома (электрона) на направление
магнитного поля численно равна магнетону
Бора.

42.

Кроме того, в этих опытах было
обнаружено новое явление. Валентный
электрон в основном состоянии атома серебра
имеет орбитальное квантовое число l = 0 (s –
состояние).
L
l
(
l
1
)
0
Но при l = 0,
(проекция момента импульса на направление
внешнего поля равна нулю).
Возник
вопрос,
пространственное
квантование какого момента импульса
обнаружилось в этих опытах, и проекция
какого магнитного момента равна магнетону
Бора?

43.

В 1925 г. студенты Геттингенского
университета
Гаудсмит
и
Уленбек
предложили существование собственного
импульса
у
механического
момента
электрона S (спина) и, соответственно,
собственного
магнитного
момента
электрона mS.
Введение понятия спина сразу объяснило
ряд затруднений, имевшихся к тому времени в
квантовой механике и в первую очередь,
результатов опытов Штерна и Герлаха.

44.

Авторы дали такое толкование спина: электрон
вращающийся волчок.
Но тогда следует, что «поверхность» волчка (электрона)
должна вращаться с линейной скоростью равной 300с, где с –
скорость света.
От такого толкования спина пришлось отказаться.
Спин, как заряд и масса, есть свойство
электрона.
П.Дирак
впоследствии
показал,
что
существование спина вытекает из решения
релятивистского
волнового
уравнения
Шредингера.
Из общих выводов квантовой механики следует,
что спин
LS S ( S 1)
S –спиновое квантовое число.

45.

Проекция спина на ось z (LSz) (ось z совпадает
с направлением внешнего магнитного поля) должна
быть квантована и вектор LSz может иметь (2S + 1)
различных ориентаций в магнитном поле.
Проекция спина на направление внешнего
магнитного поля, являясь квантовой величиной,
определяется выражением:
Lsz ms
где ms – магнитное спиновое квантовое число
может принимать только два значения
ms 1/ 2
Это и наблюдается в опыте Штерна и Герлаха.

46.

Т.о. магнитное спиновое квантовое
ms 1/ 2
число
может
принимать
два
значения.
Спиновое квантовое число S имеет только
одно значение S = 1/2.
Итак, проекция спинового механического
момента импульса на направление внешнего
магнитного поля может принимать два
значения:
LSz 1/ 2

47.

числа: n, l, m, mS.
Распределение электронов в атоме подчиняется принципу Паули: в одном атоме не
может быть более одного электрона с одинаковым набором квантовых чисел n, l, m, mS. Два
электрона, связанные в одном атоме, различаются значением, по крайней мере, одного
квантового числа.
Максимальное число электронов, находящихся в состоянии с данным главным квантовым
числом n, равно 2n 2 .
При излучении или поглощении света атом переходит из
одного состояния в другое, т.е. у волновой функции nlm изменяется набор индексов (nlm ).
Возможны не любые переходы, а только удовлетворяющие правилам отбора:
l 1; m 0, 1.
47

48.

48