Динамика-пример3

1. Теоретическая механика Примеры решения задач

Динамика
В. Л. Лапшин

2. Пример 3

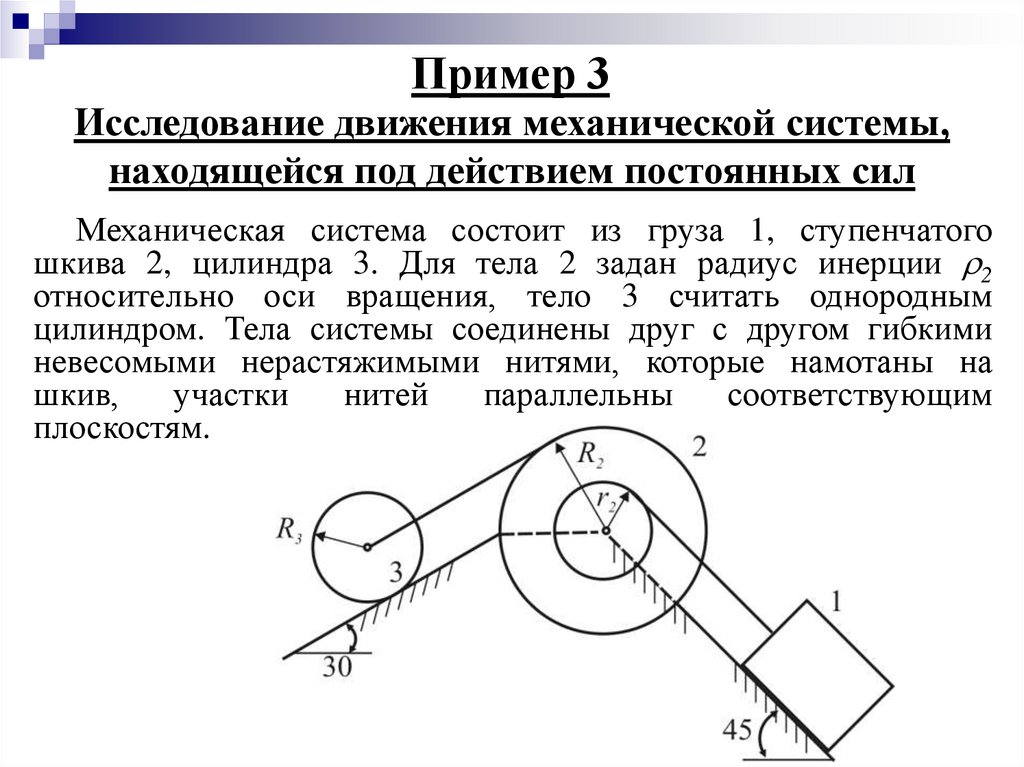
Исследование движения механической системы,
находящейся под действием постоянных сил
Механическая система состоит из груза 1, ступенчатого
шкива 2, цилиндра 3. Для тела 2 задан радиус инерции 2
относительно оси вращения, тело 3 считать однородным
цилиндром. Тела системы соединены друг с другом гибкими
невесомыми нерастяжимыми нитями, которые намотаны на
шкив,
участки
нитей
параллельны
соответствующим
плоскостям.

3.

Радиус инерции - величина , имеющая
размерность длины, с помощью которой момент
инерции тела относительно данной оси выражается
формулой:
I = М 2, где М — масса тела.
Таким образом, радиусом инерции тела
относительно оси называется такое расстояние,
квадрат которого, умноженный на массу тела, равен
моменту инерции тела относительно этой оси.
Моме́нт ине́рции — скалярная физическая
величина, мера инертности во вращательном
движении вокруг оси, подобно тому, как масса тела
является мерой его инертности в поступательном
движении.

4.

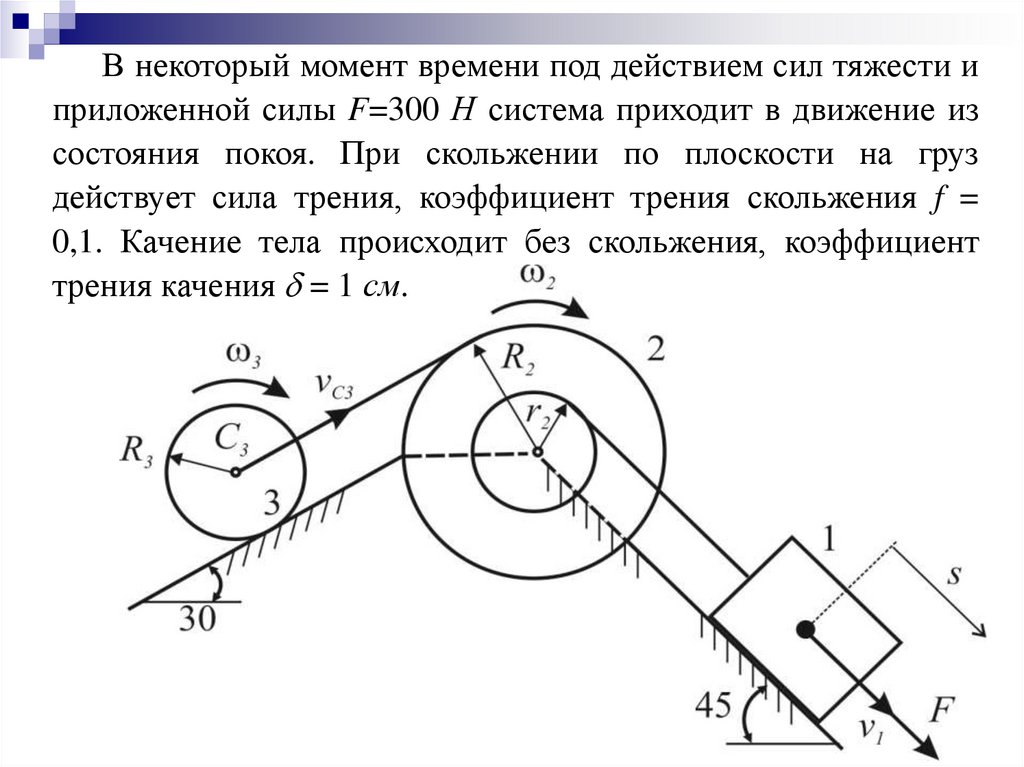
В некоторый момент времени под действием сил тяжести и
приложенной силы F=300 Н система приходит в движение из
состояния покоя. При скольжении по плоскости на груз
действует сила трения, коэффициент трения скольжения f =
0,1. Качение тела происходит без скольжения, коэффициент
трения качения = 1 см.

5.

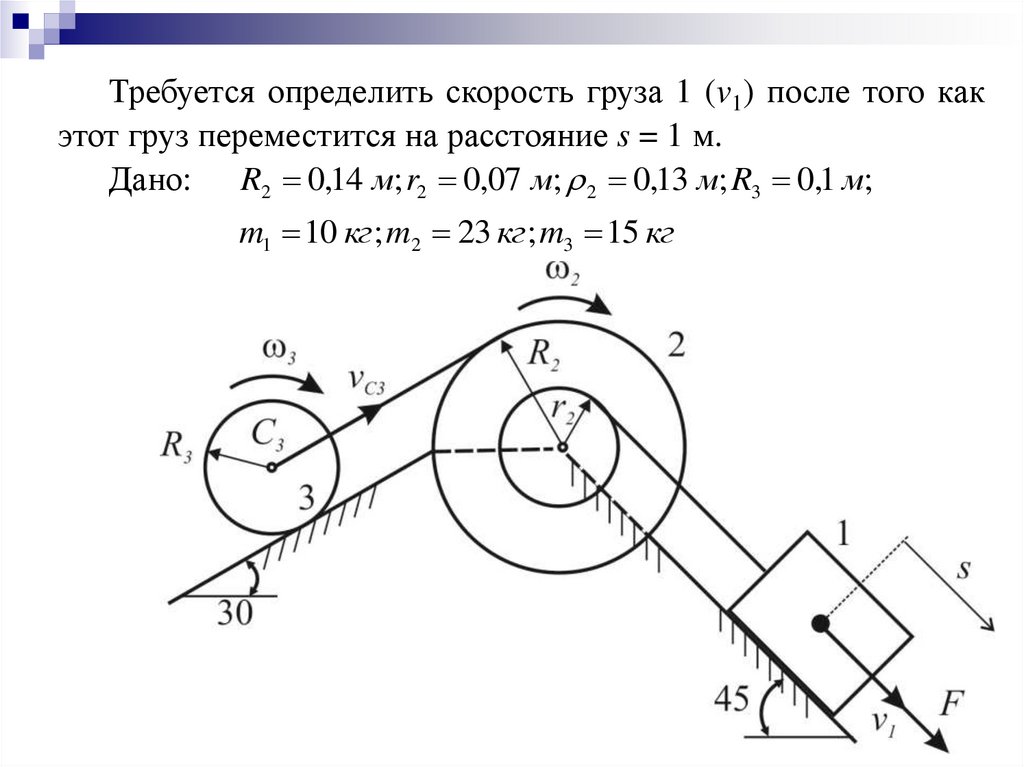
Требуется определить скорость груза 1 (v1) после того как
этот груз переместится на расстояние s = 1 м.
Дано: R2 0,14 м; r2 0,07 м; 2 0,13 м; R3 0,1 м;
m1 10 кг ; m2 23 кг ; m3 15 кг

6.

Решение
1. Рассмотрим движение механической системы. Для
определения искомой скорости воспользуемся теоремой об
изменении кинетической энергии: T T Ae Ai ,
0
Fi
Fi
где T0 и T – кинетическая энергия системы в начальном и
конечном положениях; AFie сумма работ внешних сил на
перемещениях системы из начального положения в
конечное; AFii сумма работ внутренних сил на тех же
перемещениях.
2. Для рассматриваемой системы, состоящей из
абсолютно твердых тел, соединенных нерастяжимыми
i
A
нитями, имеем:
Fi 0
Определяем Т0 и Т. Так как в начальный момент система
находилась в покое, то Т0 = 0.

7.

В результате исходное уравнение примет вид:
T AFie
Груз 1 перемещается на расстояние s. Показываем скорости
центров масс тел и угловые скорости тел. Записываем
кинетическую энергию системы Т, при этом выразим энергию
через v1: T Т 3 Т 2 Т 1
Груз 1 движется поступательно,
его
кинетическая
энергия
определяется:
1
1
2
Т1 m1v1 10v12 5v12
2
2
Ступенчатый шкив
2 вращается вокруг
неподвижной оси.
Определяем
кинетическую
энергию шкива 2:
1
Т 2 J 2 22 ; J 2 m2 22 ,
2

8.

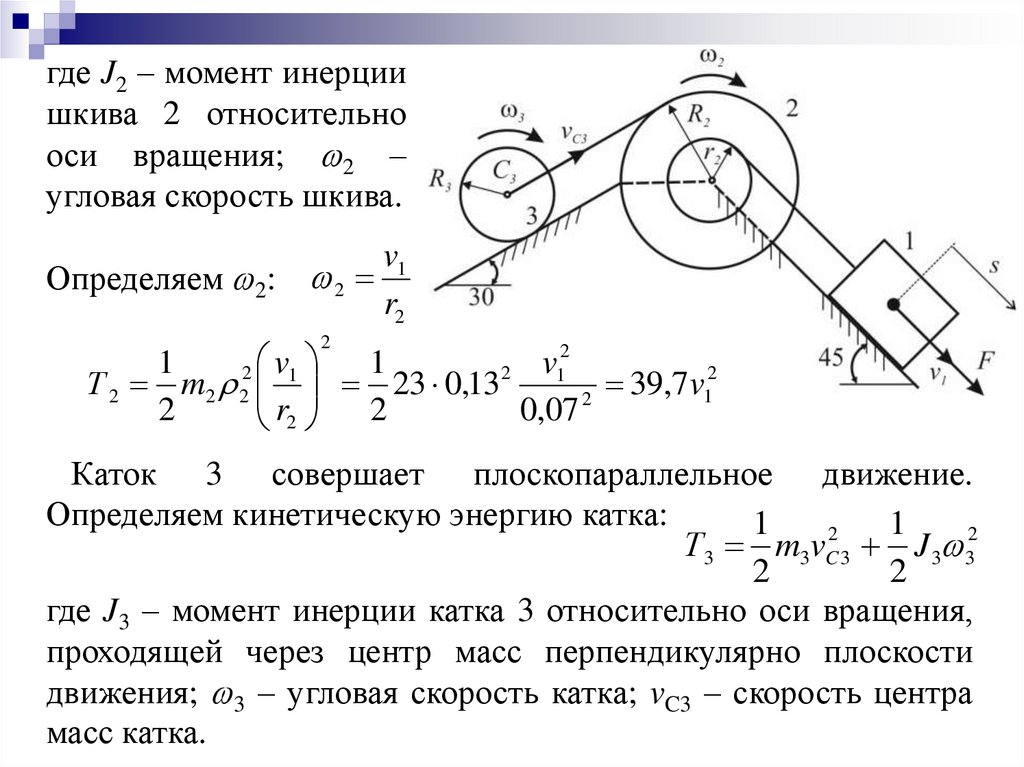
где J2 – момент инерции
шкива 2 относительно
оси вращения; 2 –
угловая скорость шкива.
v1
Определяем 2: 2
r2
2
2
v
v
1
1
Т 2 m2 22 1 23 0,13 2 1 2 39,7v12
2
2
0,07
r2
Каток 3 совершает плоскопараллельное движение.
Определяем кинетическую энергию катка:
1
1
2
Т 3 m3vC 3 J 3 32
2
2
где J3 – момент инерции катка 3 относительно оси вращения,
проходящей через центр масс перпендикулярно плоскости
движения; 3 – угловая скорость катка; vC3 – скорость центра
масс катка.

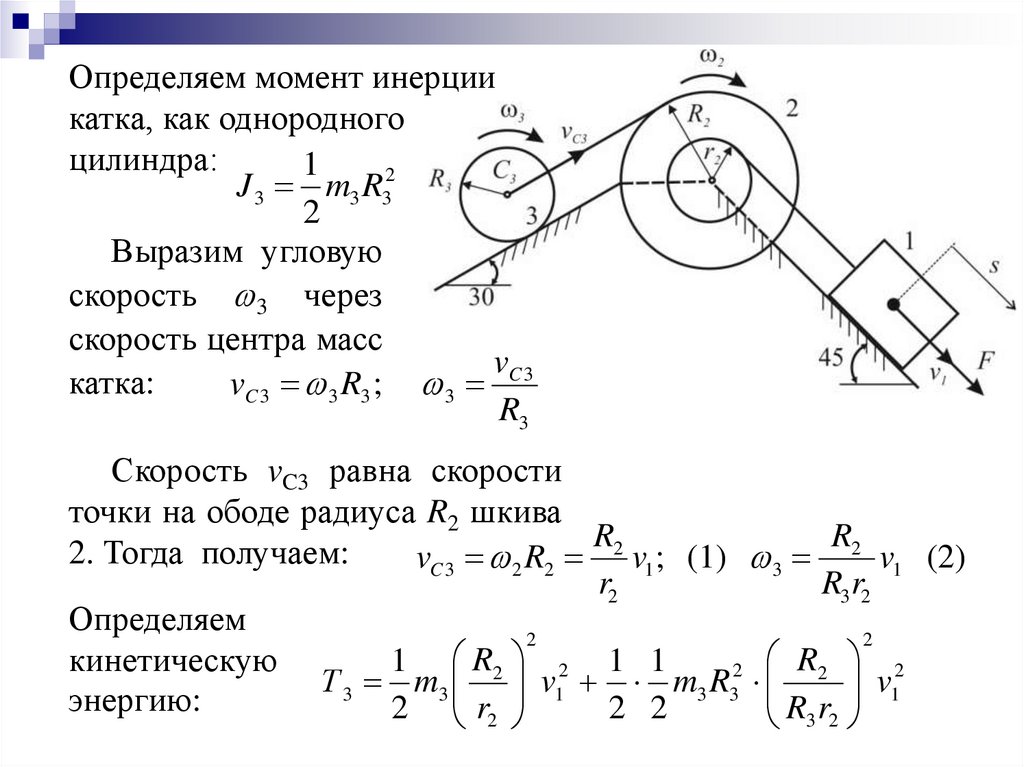
9.

Определяем момент инерции
катка, как однородного
цилиндра:
1
J 3 m3 R32
2
Выразим угловую
скорость 3 через
скорость центра масс
vC 3
катка:
vC 3 3 R3 ; 3
R3
Скорость vC3 равна скорости
точки на ободе радиуса R2 шкива
R2
R2
2. Тогда получаем:
vC 3 2 R2 v1; (1) 3
v1 (2)
r2
R3r2
Определяем
2
2
кинетическую
1 R2 2 1 1
2 R2
v12
Т 3 m3 v1 m3 R3
энергию:
2 r2
2 2
R3 r2

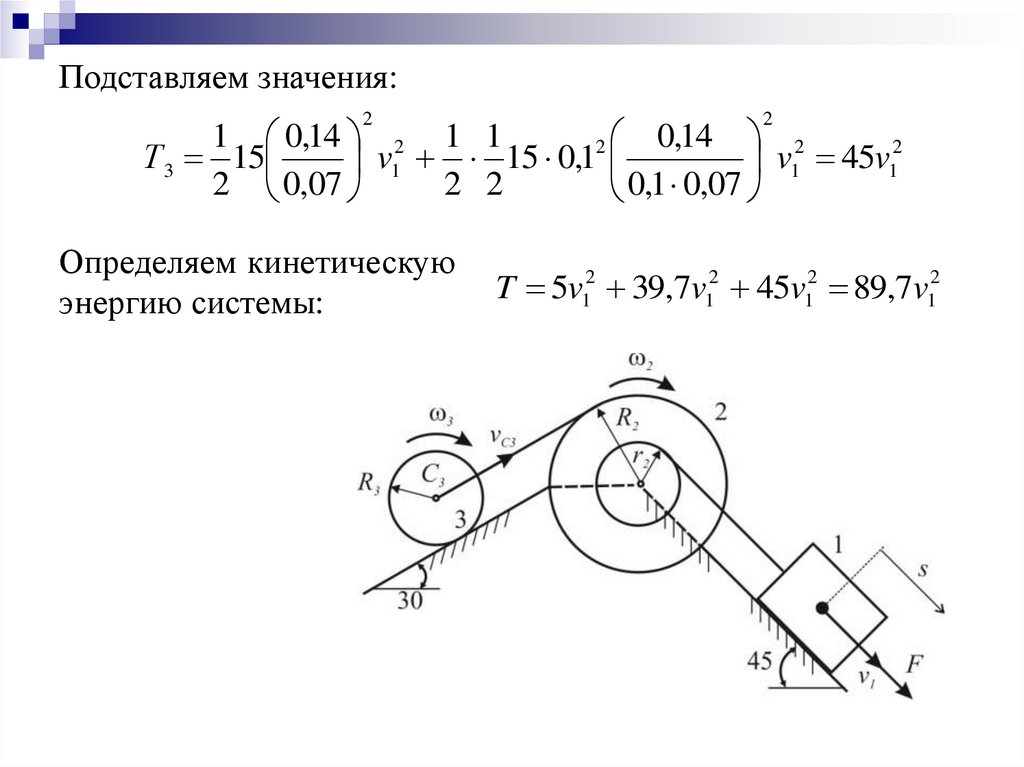
10.

Подставляем значения:
2
2
1 0,14 2 1 1
0,14 2
2
Т 3 15
v
15
0
,
1
1
v1 45v12
2 0,07
2 2
0,1 0,07
Определяем кинетическую
энергию системы:
T 5v12 39,7v12 45v12 89,7v12

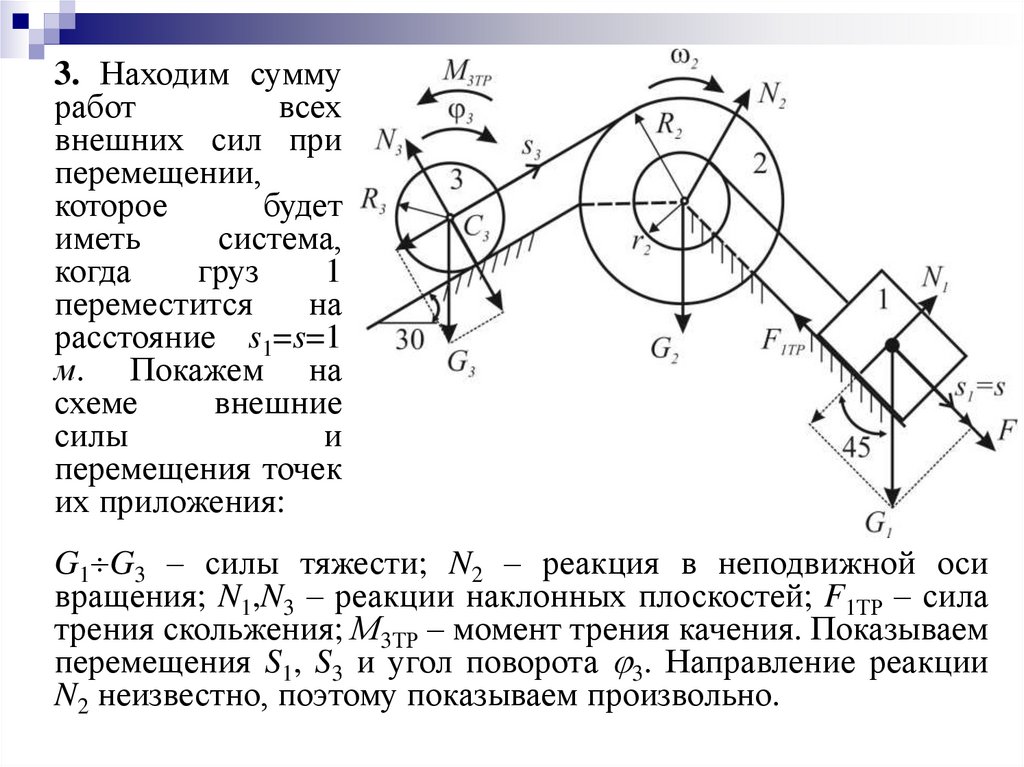
11.

3. Находим сумму
работ
всех
внешних сил при
перемещении,
которое
будет
иметь
система,
когда
груз
1
переместится
на
расстояние s1=s=1
м. Покажем на
схеме
внешние
силы
и
перемещения точек
их приложения:
G1 G3 – силы тяжести; N2 – реакция в неподвижной оси
вращения; N1,N3 – реакции наклонных плоскостей; F1ТР – сила
трения скольжения; М3ТР – момент трения качения. Показываем
перемещения S1, S3 и угол поворота 3. Направление реакции
N2 неизвестно, поэтому показываем произвольно.

12.

Определяем сумму работ внешних сил, отличных от нуля:
e
A
Fi A(G3 ) A(M 3ТР ) A(G1 ) A( F1ТР ) А( F )
Работы силы тяжести A(G2) и реакции неподвижного
шарнира A(N2) равны нулю, так как перемещения отсутствуют.
Работа силы трения скольжения F3ТР также равна нулю, так как
эта сила приложена к мгновенному центру скоростей катка 3,
являющегося в данный момент времени неподвижной точкой.
Вычисляем работы сил:
G mg ( g 9,81 м / с 2 ); FТР fN ;
N1 G1 cos 45 m1 g cos 45
10 9,81 0,71 69,7 H ;
F1ТР fN1 0,1 69,7 6,97 H ;
М 3ТР N 3 m3 g cos 30 0,01 15 9,81 0,866 1,27 Hм

13.

Модули линейных и угловых перемещений находим
учитывая, что зависимости между перемещениями будут
такими же, как и между скоростями.
R2 точек v на
Поэтому, заменяя в формулах (1),
(2)
скорости
vC 3 2 R2 v1; (1)
r2 тел на их
их линейные
перемещения s, угловые скорости
R2
3 поворота
v1 (2) , получаем:
углы
R2
0,14
R3r2
s3
s1
1 2 м;
r2
0,07
R2
0,14
3
s1
1 20 рад.
R3 r2
0,1 0,07
Вычисляем работы сил:
A(G3 ) G3 sin 30 s3
m3 g sin 30 s3
15 9,81 0,5 2 147 Дж;
A( М 3ТР ) М 3ТР 3 1,27 20 25,4 Дж ;

14.

A(G1 ) G1 sin 45 s1 m1 g sin 45 s1 10 9,81 0,71 1 69,7 Дж ;
A( F1ТР ) F1ТР s1 6,97 1 6,97 Дж ;
A( F ) F s1 300 1 300 Дж
Вычисляем сумму работ внешних сил:
e
A
Fi 147 25,4 69,7 6,97 300 190 Дж
Таким образом: T AFie ; T 89,7v12 ; 89,7v12 190
v1
190
1,46 м / с
89,7
Ответ: под действием
постоянной силы F и сил
тяжести тел груз 1 будет
двигаться вниз и после
перемещения из начального
положения на расстояние s
=1 м его скорость составит
v1 1,46 м / с