Similar presentations:
Динамика кулисного механизма
1. КУРСОВАЯ РАБОТА по теоретической механике «ДИНАМИКА КУЛИСНОГО МЕХАНИЗМА»
Министерство по образованию и науки Российской ФедерацииФГАОУ ВПО «Уральский федеральный университет
имени первого Президента России Б.Н.Ельцина»
КУРСОВАЯ РАБОТА
по теоретической механике
«ДИНАМИКА КУЛИСНОГО МЕХАНИЗМА»
Вариант: 2307017
Студент: Крупенин А.Ю.
Группа: М-230701
Преподаватель: Савина Е.А.
2. Кулисный механизм
3. Задание курсовой работы
Кулисный механизм приводится в движение из состояния покоявращающим моментом , создаваемым электродвигателем. Заданы
массы звеньев механизма; величина вращающего момента; радиус
инерции катка и радиусы его ступеней; радиус маховика,
представляющего собой сплошной однородный цилиндр, R1 = 0,36 м;
OA = 0,24 м.
Определить:
Угловую скорость маховика при его повороте на угол .
Угловое ускорение маховика при его повороте на угол .
Силу, приводящую в движение кулису в положении механизма, когда
и реакцию подшипника на оси маховика.
Силу, приложенную в центре катка и уравновешивающую механизм в
положении, когда .
m1, кг
m2, кг
m3, кг
Mд, Н·м
p3, м
R3,м
φ, рад
72
12
18
22
0,18
0,18
2π/3
4. Этап I. Кинематический анализ механизма.
R3vD
1
v2 x R3 R3 2
Следовательно,
1
v D OA sin
2
5. Этап I. Кинематический анализ механизма.
Угловую скорость катка находим поформуле
3
vD
1
OA sin
R3
2 R3
Угловое
ускорение
находим
дифференцированием угловой скорости.
3
1
1 2
OA sin
OA cos
2 R3
2 R3
6. Этап I. Кинематический анализ механизма.
Переносноеускорение
точки
определяет ускорение кулисы в
поступательном движении
a
2x
A x OA sin
a
2
А
ее
OA cos
Ускорение центра катка находим по формуле
1
1
a D v D OA sin 2 OA cos
2
2
7. 1.2. Уравнения геометрических связей
Как и раньше, начало координат помещаем вточку , ось направляем вправо, ось – вверх.
Уравнения связей:
x A OA cos
y A OA sin
xD xD0
yC 2 0
1
OA cos
2
xC 2 xC 20 OA cos
3
y D R3
1
OA cos
2 R3
Последние два соотношения получены интегрированием равенств
1
x D OA sin
2
3
1
OA sin
2 R3
8. Этап II. Угловая скорость и угловое ускорение маховика.
2.1 Для определения угловой скорости маховика воспользуемсятеоремой об изменении кинетической энергии в интегральной
форме
Так как по условию задачи механизм приводится в движение из
состояния покоя, то
Так как система состоит из абсолютно твердых тел, то работа
внутренних сил равна нулю
9. Этап II. Угловая скорость и угловое ускорение маховика.
Кинетическая энергия вращающегося маховика вычисляется по формулеКулиса совершает поступательное движение, следовательно
Кинетическая энергия катка, совершающего плоское движение:
Момент инерции маховика относительно оси вращения определяется
формулой
Момент инерции катка вычисляется по формуле
10. Этап II. Угловая скорость и угловое ускорение маховика.
После тождественных преобразованийопределяется равенством:
кинетическая
энергия
системы
I пр ( ) 4.6656 1.2096 sin 2
I пр ( * ) 5,573
Элементарная работа определяется равенством:
Работа при повороте маховика на угол φ*
Подставим выражения, полученные для вычисления кинетической энергии и
работы внешних сил, в теорему об изменении кинетической энергии
Подставляя числовые значения, получаем
рад
4,066
с
*
11. Этап II. Угловая скорость и угловое ускорение маховика.
2.2 Для определения углового ускорения маховика воспользуемся теоремой обизменении кинетической энергии в дифференциальной форме
Вычислим производную от кинетической энергии по времени
dI пр
d
1.2096 sin 2
*
dI пр
d
1,0475
Вычислим мощность внешних сил при повороте маховика на угол φ*.
1 5,502
Выразим дифференциальное уравнение движения механизма
(4.6656 1.2096 sin 2 ) 0.6048 sin (2 ) 2 22
рад
с2
12. Этап III. Реакции связей и уравновешивающая сила.
Маховик совершает вращательное движение.Система сил инерции приводится к паре сил с моментом M I 1 1
Составим уравнения равновесия.
Fkx 0;
X O N A 0,
Fky 0;
YO 0,
mO Fk 0; M Д M N A y A 0;
NA
MД M
yA
M Д I 1
yA
N A 55,045Н
YO 0 Н ,
X O 55,045Н .
Сила, приводящая в движение кулису, по третьему закону динамики равна
реакции кулисы и направлена в противоположную сторону.
13. Этап III. Реакции связей и уравновешивающая сила.
Воспользуемся принципом возможных перемещенийСоставим уравнение в аналитическом виде
Используя уравнения связей
y D R3
находим вариации координат y D 0
1
x D x D 0 OA sin
2
1
x D OA cos
2
Подстановка этих соотношений в уравнение принципа виртуальных
перемещений дает
F 366,667 Н
x
14. Этап IV. Дифференциальное уравнение движения кулисного механизма.
Запишем уравнение Лагранжа второго рода в общем видеОбобщенная сила определяется отношением
Тогда
Кинетическая энергия определяется выражением, найденным ранее
I пр ( ) 4.6656 1.2096 sin
2
dI пр
d
Выразим дифференциальное уравнение движения механизма
(4.6656 1.2096 sin 2 ) 0.6048 sin (2 ) 2 22
1.2096 sin 2
15. Этап IV. Дифференциальное уравнение движения кулисного механизма.
Составление уравнения движения машины.Машиной называется совокупность твердых тел (звеньев), соединенных между
собой так, что положение и движение любого звена определяется положением
и движением одного звена, называемого ведущим.
Если ведущим звеном
записывается в виде
является
кривошип,
то
уравнение
движения
Приведенный вращающий момент определяется равенством
Для рассматриваемого кулисного механизма
Дифференциальные уравнения движения механизма, полученные с помощью
теоремы об изменении кинетической энергии, уравнения Лагранжа и
уравнение движения машины совпадают.
(4.6656 1.2096 sin 2 ) 0.6048 sin (2 ) 2 22
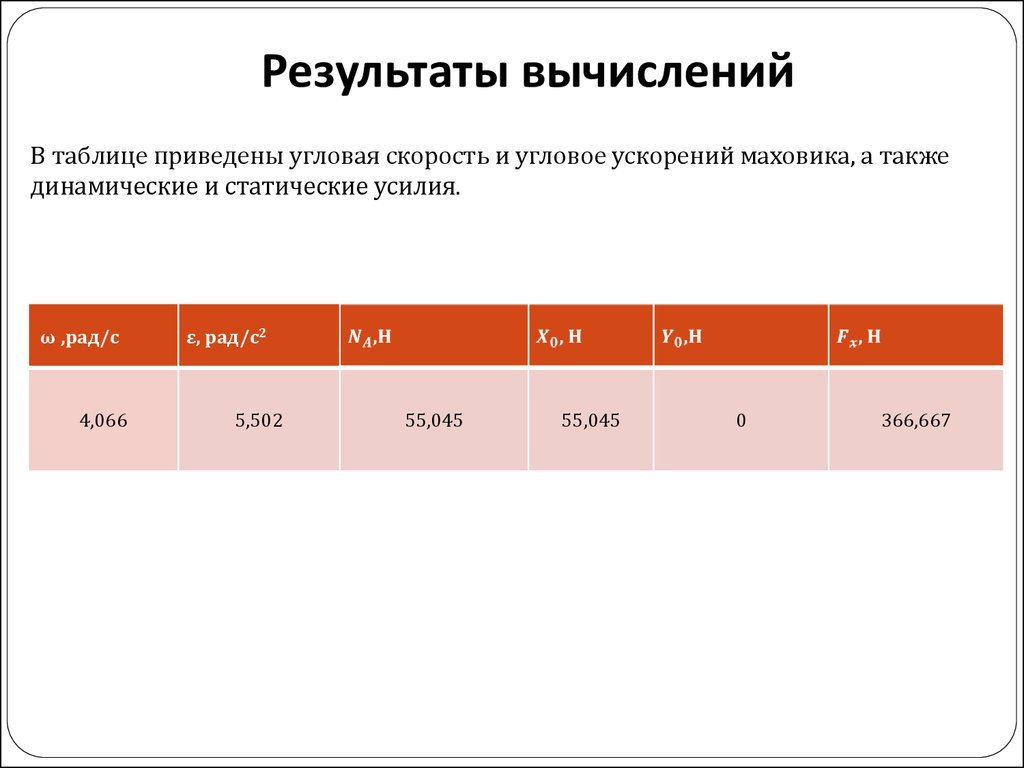
16. Результаты вычислений
В таблице приведены угловая скорость и угловое ускорений маховика, а такжединамические и статические усилия.
ω ,рад/с
4,066
ε, рад/с2
5,502
55,045
55,045
0
366,667















 mechanics
mechanics industry
industry








