Динамика кулисного механизма

1. Курсовая работа «Динамика кулисного механизма» Вариант 2310045

Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего
профессионального образования
«Уральский федеральный университет имени первого Президента России
Б.Н.Ельцина»
Кафедра теоретической механики
Курсовая работа
«Динамика кулисного механизма»
Вариант 2310045
Выполнил
Студент:Вахрушев И.В.
Группа ММ-231004
Екатеринбург
2014

2. Задание

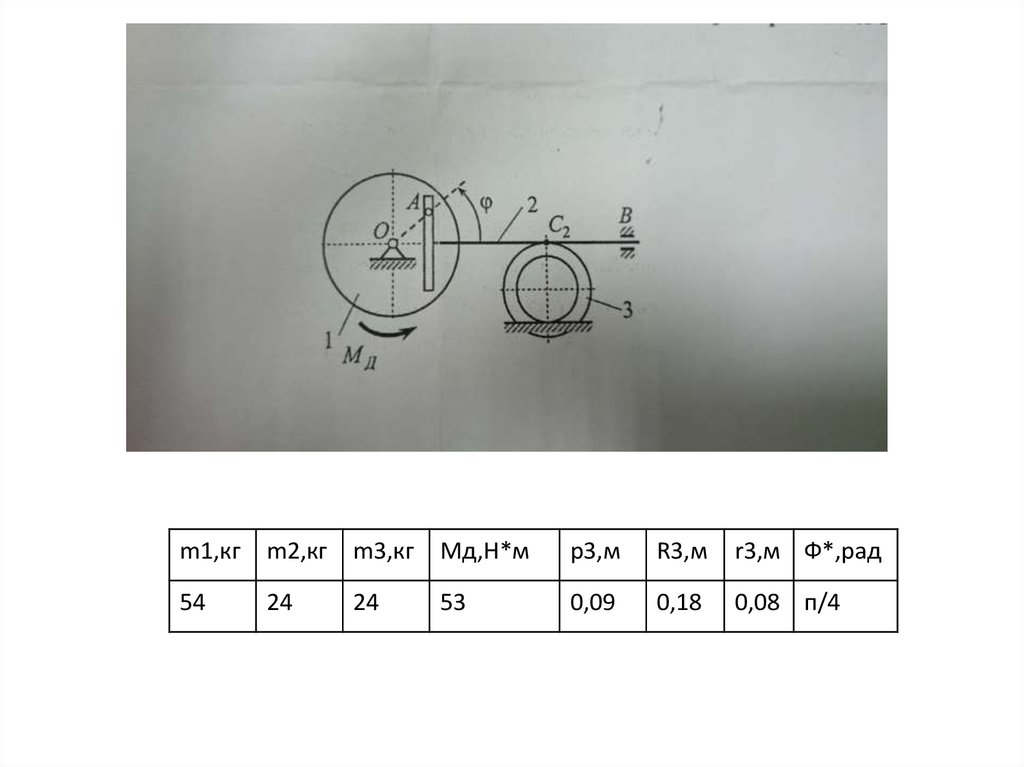
• Кулисный механизм (рис. 1), состоящий из маховика 1, кулисы 2
и катка 3, расположен в горизонтальной плоскости и
приводится в движение из состояния покоя вращающим
моментом , создаваемым электродвигателем. Заданы массы
звеньев механизма; величина вращающего момента; радиус
инерции катка и радиусы его ступеней; радиус маховика,
представляющего собой сплошной однородный цилиндр, R1 =
0,36 м; OA = 0,24 м. (табл. 1).
• Определить:
• Угловую скорость маховика при его повороте на угол .
• Угловое ускорение маховика при его повороте на угол .
• Силу, приводящую в движение кулису в положении механизма,
когда и реакцию подшипника на оси маховика.
• Силу, приложенную в центре катка и уравновешивающую
механизм в положении, когда .
Записать дифференциальное уравнение движение
механизма, используя уравнение Лагранжа второго рода и
уравнение движения машины.

3.

m1,кг
m2,кг
m3,кг
Mд,Н*м
p3,м
R3,м
r3,м Ф*,рад
54
24
24
53
0,09
0,18
0,08 п/4

4. I этап Кинематический анализ механизма

• 1.1. Определение кинематических
характеристик
Используя теорему сложения скоростей и ускорений, найдем скорость и
ускорение поступательно движущейся кулисы.
v
2x
A x
v
OA sin
a2x vA x 2OA cos OA sin
Угловую скорость катка находим как отношение скорости его центра к
расстоянию до мгновенного цента скоростей, угловое ускорение
дифференцированием угловой скорости.
vC 3 y
1
1
1
2
OA
cos
OA sin
3
OA cos
3
r3 R3
r3 R3
R3
r3 R3

5. I этап Кинематический анализ механизма

• 1.2. Уравнения геометрических связей
Уравнения связей:
x A OA cos
xC 3
xC 3
y A OA sin
r3
xc3o
OA sin
r3 R3
r3
OA cos
r3 R3
xC 2 xC 20 OA cos
1
3
OA sin
r3 R3
1
3
OA cos
r3 R3

6. II этап Определение угловой скорости и углового ускорения маховика.

• 2.1. Кинетическая энергия системы
Кинетическую энергию находим как сумму кинетических энергий его звеньев.
После тождественных преобразований:
2
I пр
2
2
r3
mR
1
2
2
I пр
m2 ( OA sin ) m3
OA sin m3 3
OA sin
2
r3 R3
r3 R3
2
1 1
I пр 51.53 кг м2
2

7. II этап Определение угловой скорости и углового ускорения маховика.

• 2.2. Производная кинетической энергии по времени
Производную кинетической энергии по времени находим по правилу
вычисления производной произведения и производной сложной функции
dT 1 dI пр
2 I пр
dt 2 d
dI пр
d
dI пр
d
m r R m
2
2
0.099
3
3
3
2
r3 R3
здесь
2
3
r32
OA
2
sin 2

8. II этап Определение угловой скорости и углового ускорения маховика.

• 2.4. Определение угловой скорости
маховика при его повороте на угол φ*
Для определения угловой скорости маховика применяем теорему об
изменении кинетической энергии. После подстановки мы получим:
I пр 2
4 M
Д
2
4
где I пр ,
0.24 0.71
6.6( м / с 2 )
0.08 0.18
4
I пр 51.53
4

9. II этап Определение угловой скорости и углового ускорения маховика.

• 2.5. Определение углового ускорения
маховика при его повороте на угол φ*
Воспользуемся теоремой об изменении кинетической. После
подстановки мы получим:
1 dI пр 2
I пр
M Д
2 d
подставляя значения получим,
1
2
53 0.099 6.6
2
1
4
51.53

10. Краткие итоги II этапа

,
.
ω= 6,6 рад/с
ε= 9.8 рад/с2

11. III этап Определение реакций связей и уравновешивающей силы

• 3.1. Определение реакций внешних и
внутренних связей в положении φ*
С помощью принципа д`Аламбера определим реакцию подшипника на
оси маховика и силу, приводящую в движение кулису.
Fkx 0;
X O N A 0,
Fky 0;
YO 0,
mO Fk 0; M Д M N Ax y A 0;

12. III этап Определение реакций связей и уравновешивающей силы

NA
M MД
yA
NA
I1 M Д
yA
51.53 9.8 53
0.24 sin
144.87 Н
4
X O N Ax 144.87 Н
YO 0,

13. III этап Определение реакций связей и уравновешивающей силы

• 3.2. Определение силы
уравновешивающей кулисный механизм
Найдем силу, которую надо приложить к оси катка, чтобы она
уравновешивала действие момента, создаваемого электродвигателем
в положении маховика .
M Д r3 R3
53 0.08 0,16
F x
R3OA sin 0.8 0.24 0.013

14. Краткие итоги III этапа

,
.
FA = 144.87H
X O = -144.87H
YO = 0,H
FC3 =5512H

15. IV этап Составление дифференциального уравнения движения кулисного механизма

• 4.1. Уравнение Лагранжа второго рода
Подстановка найденных значений в уравнение Лагранжа дает
I пр
1 dI пр 2
M Д подставляя точные значения получаем
2 d
1
(3.24 2.147 sin 2 ) (2.147 2 cos sin ) 2 M Д при угле
2
4
1
2
(
3
.
24
2
.
147
sin
)
(2.147 2 cos sin ) 2 53
Получаем
2

16. IV этап Составление дифференциального уравнения движения кулисного механизма

• 4.2. Уравнение движения машины
Подстановка найденных значений в уравнение Лагранжа дает
I пр
1 dI пр 2
M пр подставляя точные значения получаем
2 d
1
(3.24 2.147 sin 2 ) (2.147 2 cos sin ) 2 M пр при угле
2
4
1
2
(
3
.
24
2
.
147
sin
)
(2.147 2 cos sin ) 2 53
получаем
2

17. Итоговые ответы

FА,144.87,H
X0= -144.87 , H
YO= 0,H
Fc3= 5512,H
ω= 6,6рад/с
ε= 9,8 рад/с2