7-lek-kolebanija-volny_фт2024

1. Колебания и волны

2024 г.
1

2. План

1.
Колебательные процессы. Гармонические колебания. Понятие о
спектральном разложении.
2. Дифференциальное уравнение гармонических колебаний.
3. Пружинный, физический и математический маятники.
4. Энергия гармонического осциллятора.
5. Сложение колебаний.
5а. Сложение колебаний одинаковой частоты, происходящих вдоль
одной прямой.
5b. Сложение взаимно перпендикулярных колебаний одинаковой
частоты.
5с. Сложение взаимно перпендикулярных колебаний кратных частот.
Фигуры Лиссажу.
1. Затухающие колебания.
2. Вынужденные колебания.
3. Упругие волны. Основные понятия.
4. Дифференциальное уравнение волны.
5. Стоячие волны.
6. Скорость упругих волн.
7. Энергия волны. Групповая скорость. Вектор плотности потока
энергии (вектор Умова). Интенсивность волны.
8. Элементы акустики.
9. Эффект Доплера для звуковых волн.
2

3. Колебания (колебательные движения)- изменения состояния, обладающие той или иной степенью повторяемости во времени.

Колебательные процессы.
Колебания (колебательные движения)изменения состояния, обладающие той или
иной степенью повторяемости во времени.
Колебания могут иметь различную физическую
природу.
Колебания различают:
•по характеру физических процессов
•по характеру зависимости от времени.

4.

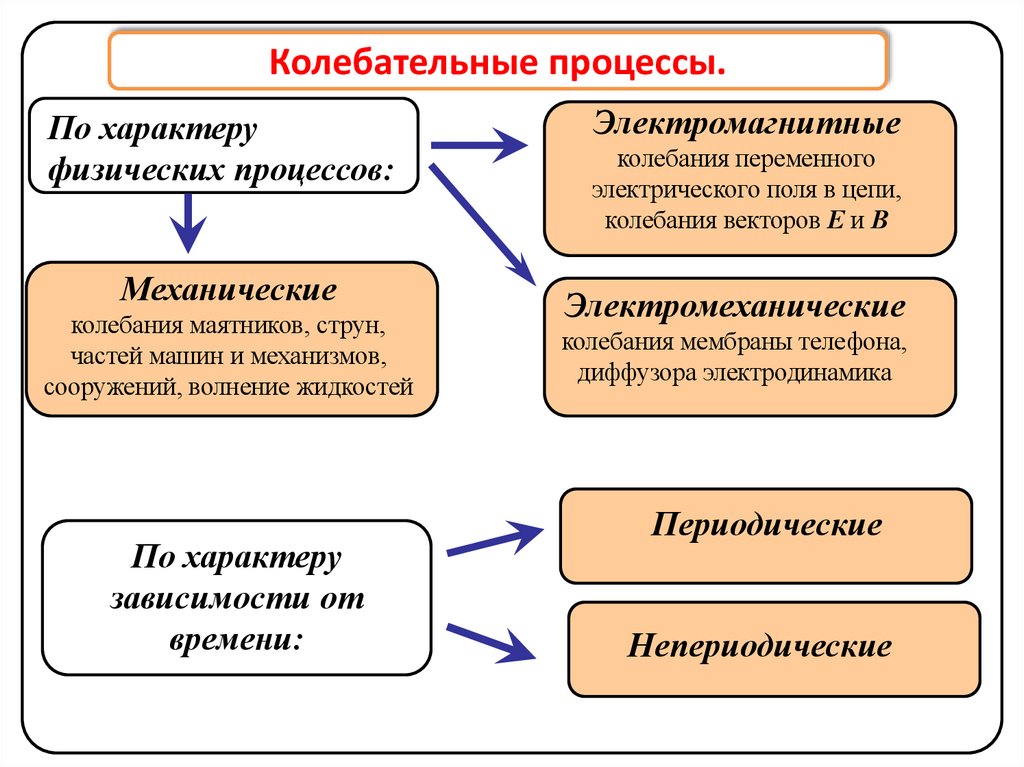
Колебательные процессы.
По характеру
физических процессов:
Механические
колебания маятников, струн,
частей машин и механизмов,
сооружений, волнение жидкостей
По характеру
зависимости от
времени:
Электромагнитные
колебания переменного
электрического поля в цепи,
колебания векторов Е и В
Электромеханические
колебания мембраны телефона,
диффузора электродинамика
Периодические
Непериодические

5.

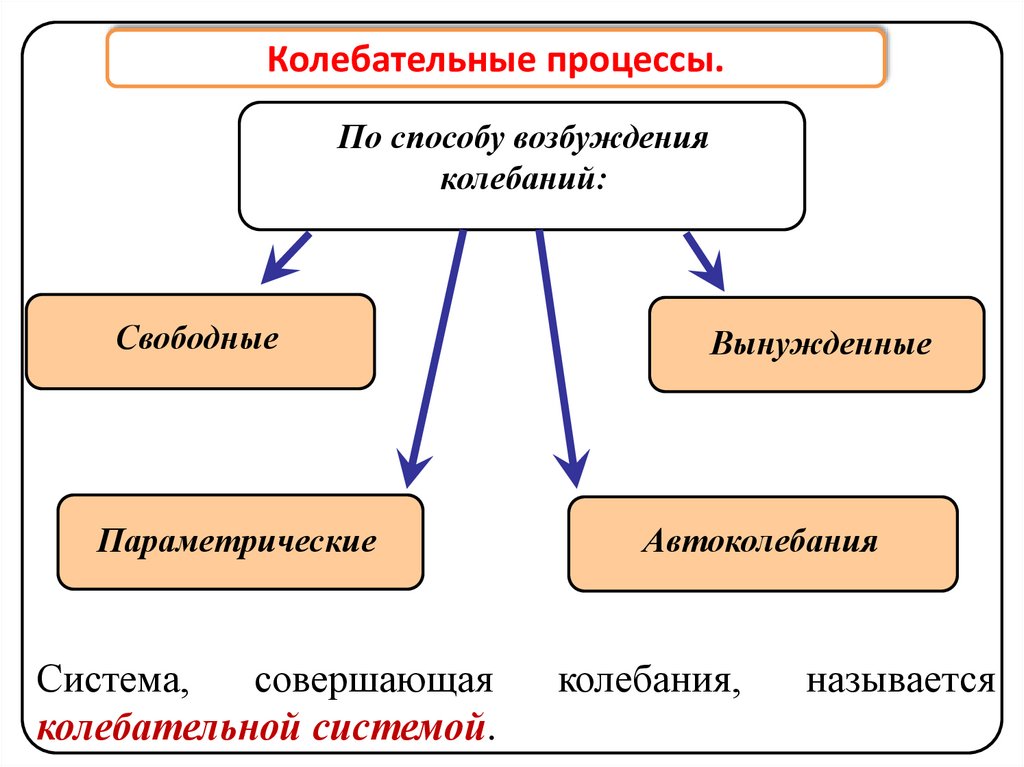
Колебательные процессы.
По способу возбуждения
колебаний:
Свободные
Параметрические
Система,
совершающая
колебательной системой.
Вынужденные
Автоколебания
колебания,
называется

6.

Колебательные процессы.
Колебания называются периодическими, если
значения физических величин, изменяющихся
в процессе колебаний, повторяются через
равные промежутки времени.
Периодические процессы можно представить
как наложение гармонических колебаний.
Гармонические колебания – колебания, при
которых колеблющаяся величина изменяется со
временем по закону синуса или косинуса.

7.

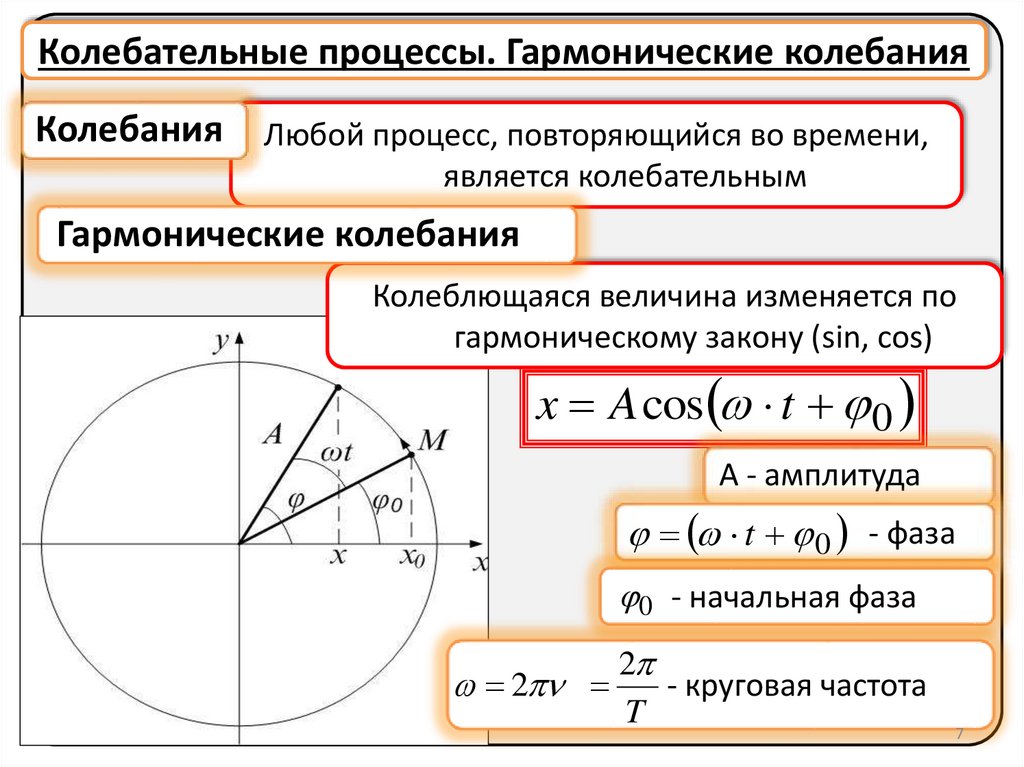
Колебательные процессы. Гармонические колебания
Колебания
Любой процесс, повторяющийся во времени,
является колебательным
Гармонические колебания
Колеблющаяся величина изменяется по
гармоническому закону (sin, cos)
x A cos t 0
А - амплитуда
t 0 - фаза
0 - начальная фаза
2
2
- круговая частота
T
7

8.

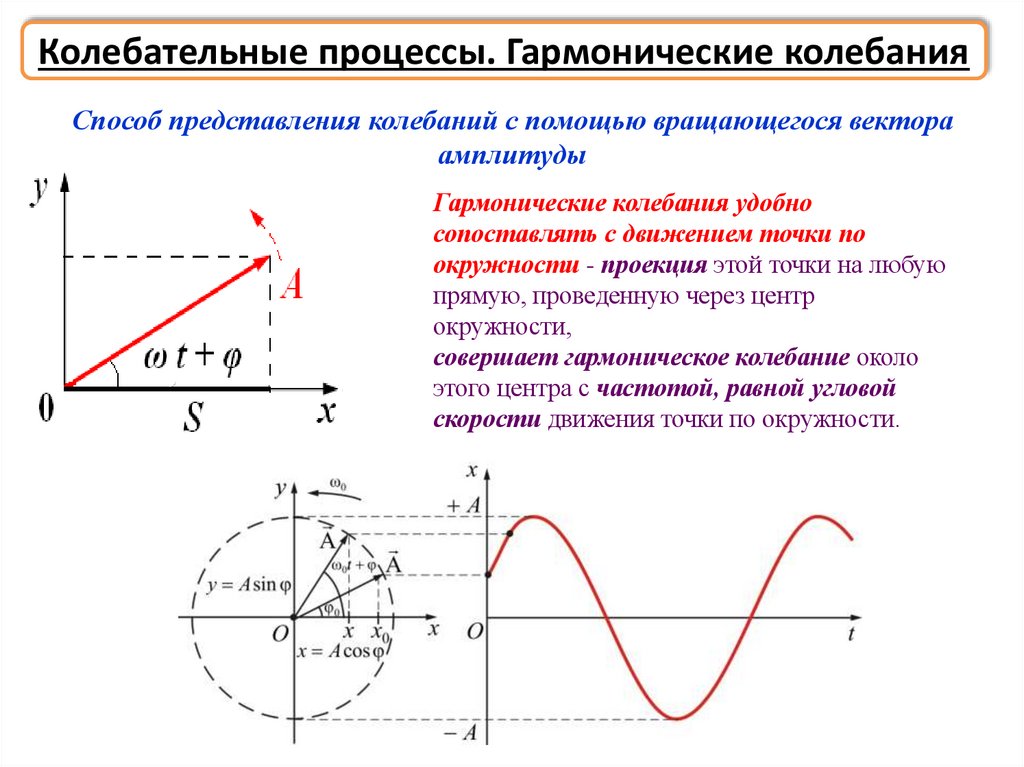
Колебательные процессы. Гармонические колебания
Способ представления колебаний с помощью вращающегося вектора
амплитуды
Гармонические колебания удобно
сопоставлять с движением точки по
окружности - проекция этой точки на любую
прямую, проведенную через центр
окружности,
совершает гармоническое колебание около
этого центра с частотой, равной угловой
скорости движения точки по окружности.

9.

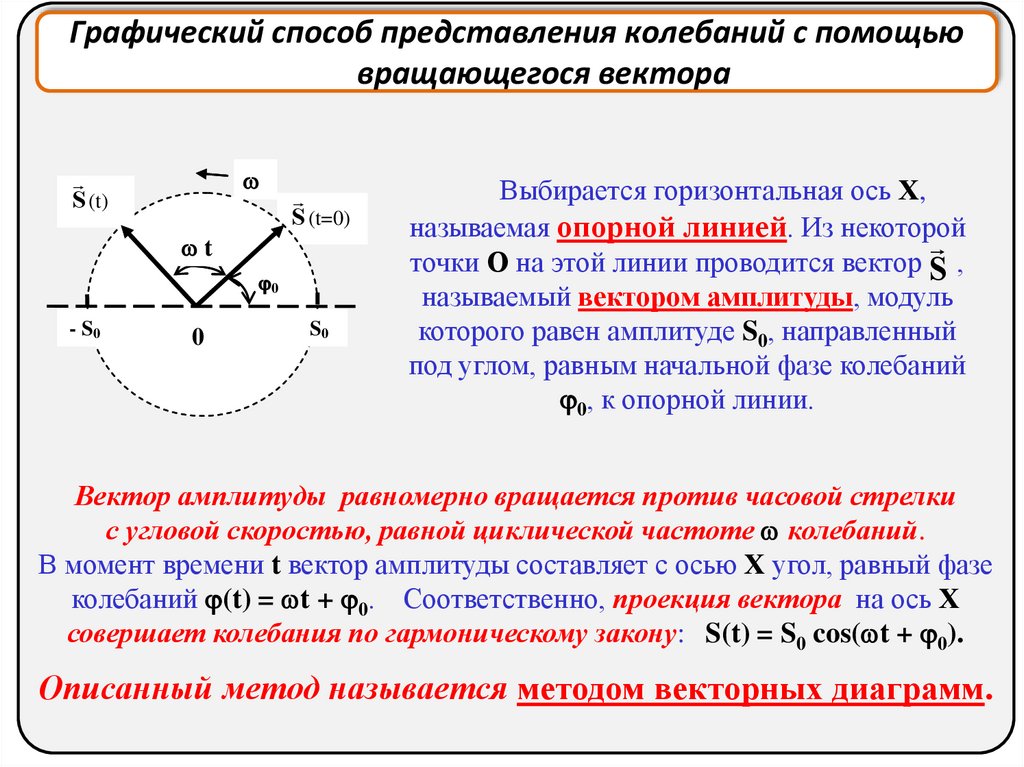
Графический способ представления колебаний с помощью
вращающегося вектора
S (t)
S (t=0)
t
0
- S0
0
S0
Выбирается горизонтальная ось Х,
называемая опорной линией. Из некоторой
точки О на этой линии проводится вектор S ,
называемый вектором амплитуды, модуль
которого равен амплитуде S0, направленный
под углом, равным начальной фазе колебаний
0, к опорной линии.
Вектор амплитуды равномерно вращается против часовой стрелки
с угловой скоростью, равной циклической частоте колебаний.
В момент времени t вектор амплитуды составляет с осью Х угол, равный фазе
колебаний (t) = t + 0. Соответственно, проекция вектора на ось Х
совершает колебания по гармоническому закону: S(t) = S0 cos( t + 0).
Описанный метод называется методом векторных диаграмм.

10.

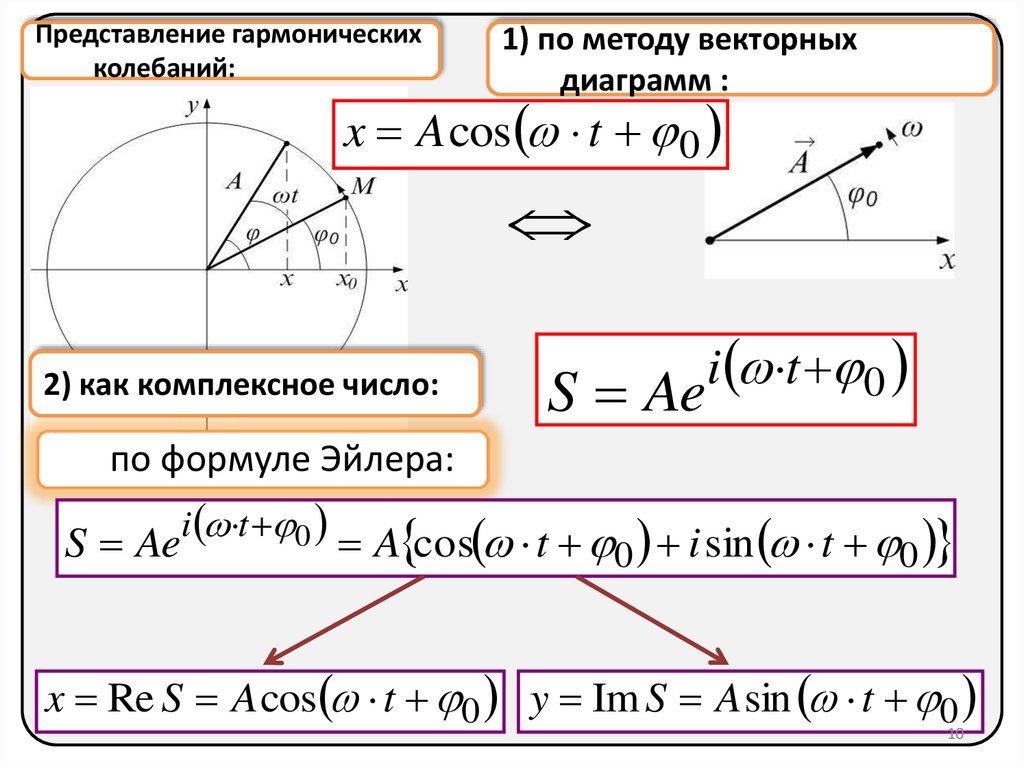
Представление гармонических
колебаний:
1) по методу векторных
диаграмм :
x A cos t 0
2) как комплексное число:
S Ae
i t 0
по формуле Эйлера:
S Aei t 0 A cos t 0 i sin t 0
x Re S A cos t 0 y Im S A sin t 0
10

11.

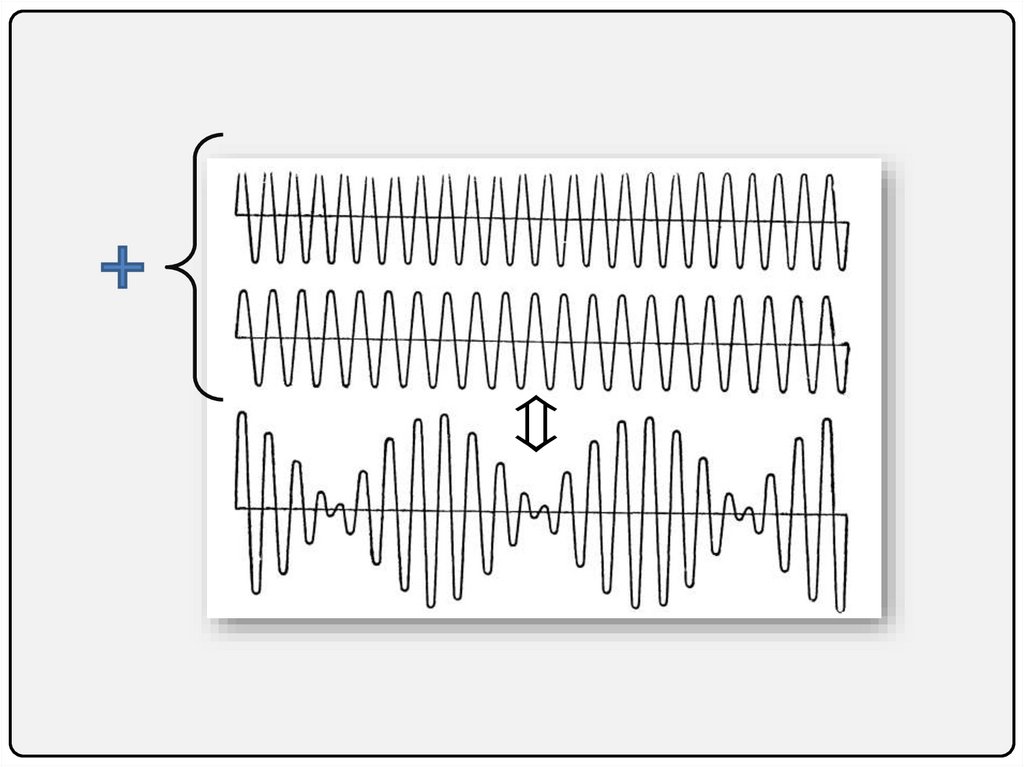
Понятие о спектральном разложении. Ряд Фурье
Теорема Фурье:
любую периодическую функцию f(t) можно
представить в виде ряда Фурье
(разложить по гармоническим составляющим)
f t f t T
T
2
0
f t a0 an cos n 0t bn sin n 0t
n 1
Для чётной функции:
f t f t
bn 0
f t a0 an cos n 0t
n 1
11

12.

Понятие о спектральном разложении. Ряд Фурье
f t a0 an cos n 0t bn sin n 0t
n 1
Гармонические
составляющие
12

13.

14.

Дифференциальное уравнение гармонических колебаний
x A cos t 0
x A sin t 0
a x 2 A cos t 0 2 x
2
x x 0
Решение этого дифференциального
уравнения – гармоническая функция:
Если вторая производная по времени какой-либо
физической величины пропорциональна самой величине с
противоположным знаком, то данная физическая величина
изменяется со временем по гармоническому закону
Сила пропорциональна смещению
F ma m 2 x kx
(квазиупругая, возвращающая)
k m 2
14

15.

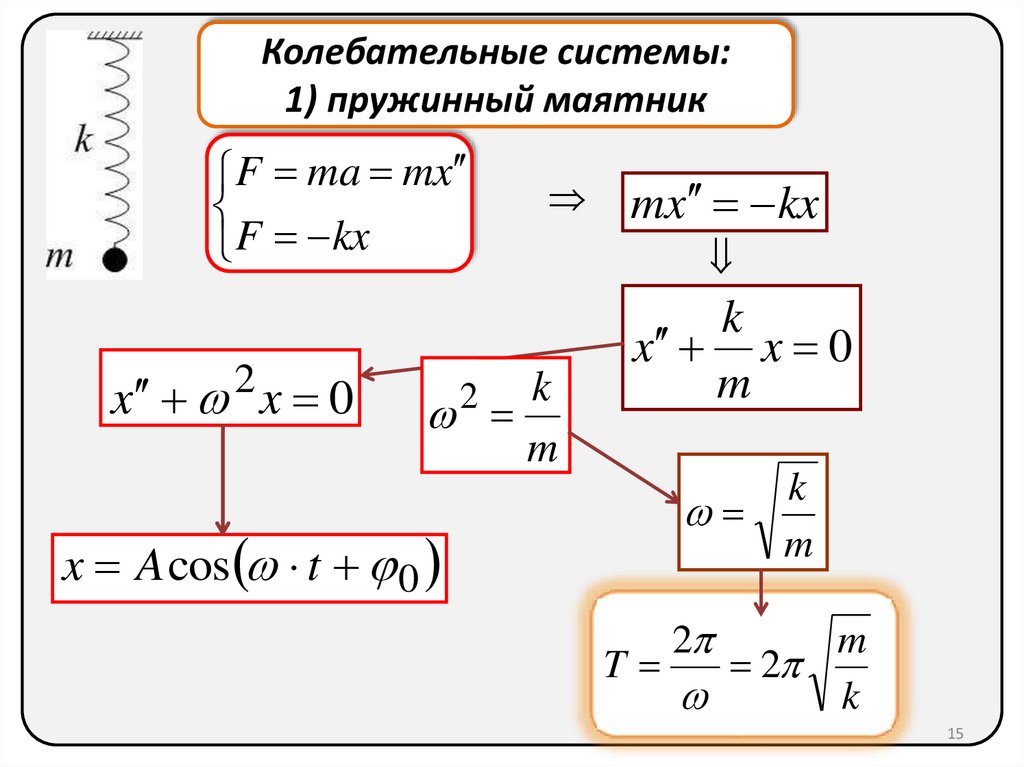
Колебательные системы:
1) пружинный маятник
F ma mx
F kx
x x 0
2
k
m
x A cos t 0
2
mx kx
k
x x 0
m
k
m
2
m
T
2
k
15

16.

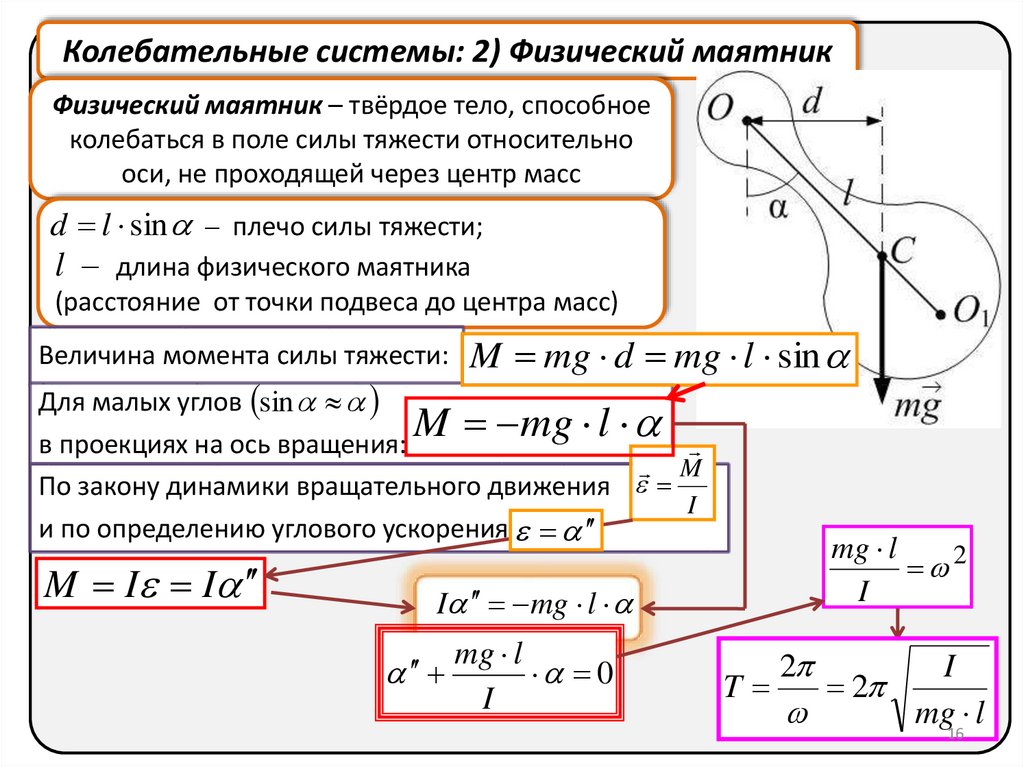
Колебательные системы: 2) Физический маятник
Физический маятник – твёрдое тело, способное
колебаться в поле силы тяжести относительно
оси, не проходящей через центр масс
d l sin – плечо силы тяжести;
l – длина физического маятника
(расстояние от точки подвеса до центра масс)
Величина момента силы тяжести:
M mg d mg l sin
Для малых углов sin
M mg l
в проекциях на ось вращения:
M
По закону динамики вращательного движения
I
и по определению углового ускорения
M I I
mg l
2
I
I mg l
mg l
0
I
2
I
T
2
mg16 l

17.

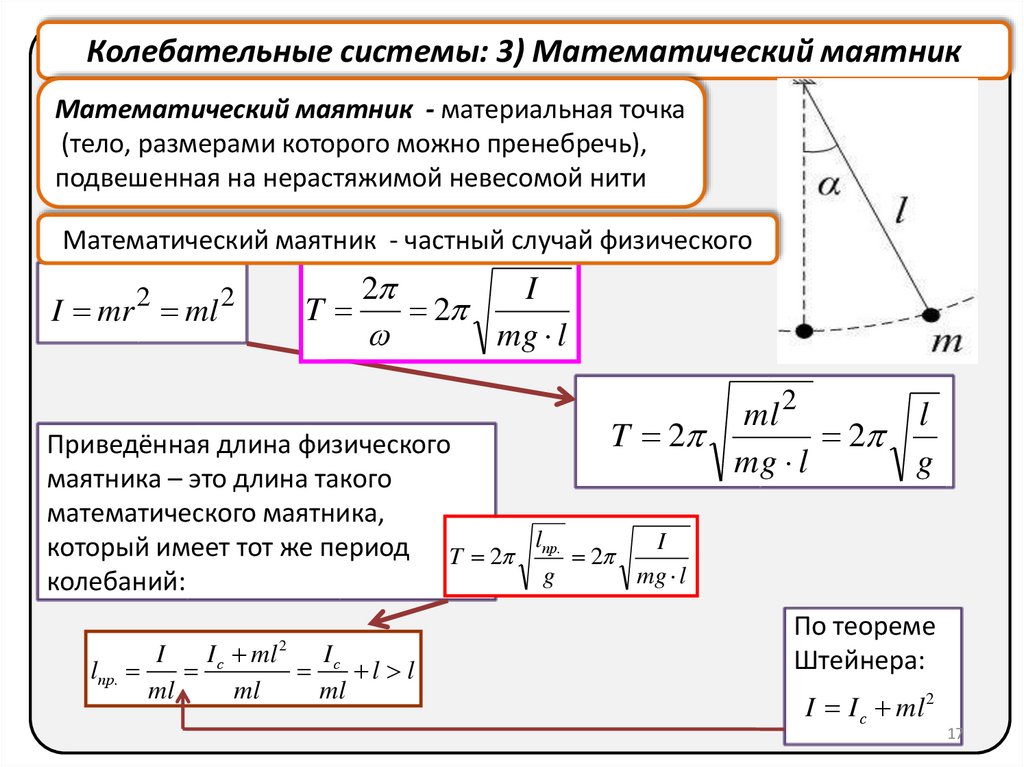
Колебательные системы: 3) Математический маятник
Математический маятник - материальная точка
(тело, размерами которого можно пренебречь),
подвешенная на нерастяжимой невесомой нити
Математический маятник - частный случай физического
2
I mr ml
2
I
T
2
mg l
2
ml 2
l
T 2
2
mg l
g
Приведённая длина физического
маятника – это длина такого
математического маятника,
который имеет тот же период T 2 lпр. 2 I
g
mg l
колебаний:
lпр.
I
I ml
I
с
с l l
ml
ml
ml
2
По теореме
Штейнера:
I I с ml 2
17

18.

Энергия гармонического осциллятора
Полная энергия:
m 2 kx2
W Wкин. Wпот.
2
2
x A cos t 0
x A sin t 0
k m 2
Гармониический
осциллятор — система,
которая при выведении
её из положения
равновесия испытывает
действие возвращающей
силы,
пропорциональной
смещению
m 2 A2 sin 2 t 0 k A2 cos2 t 0 m 2 A2
W
2
2
2
Полная энергия сохраняется; переходит из кинетической
в потенциальную и обратно
Максимальные значения:
m 2 A 2
W
2
m 2 A2 k A2
Wкин. max Wпот. max
2
2
Средние значения:
W m 2 A2 k A2
Wкин. Wпот.
2
4
4
18

19.

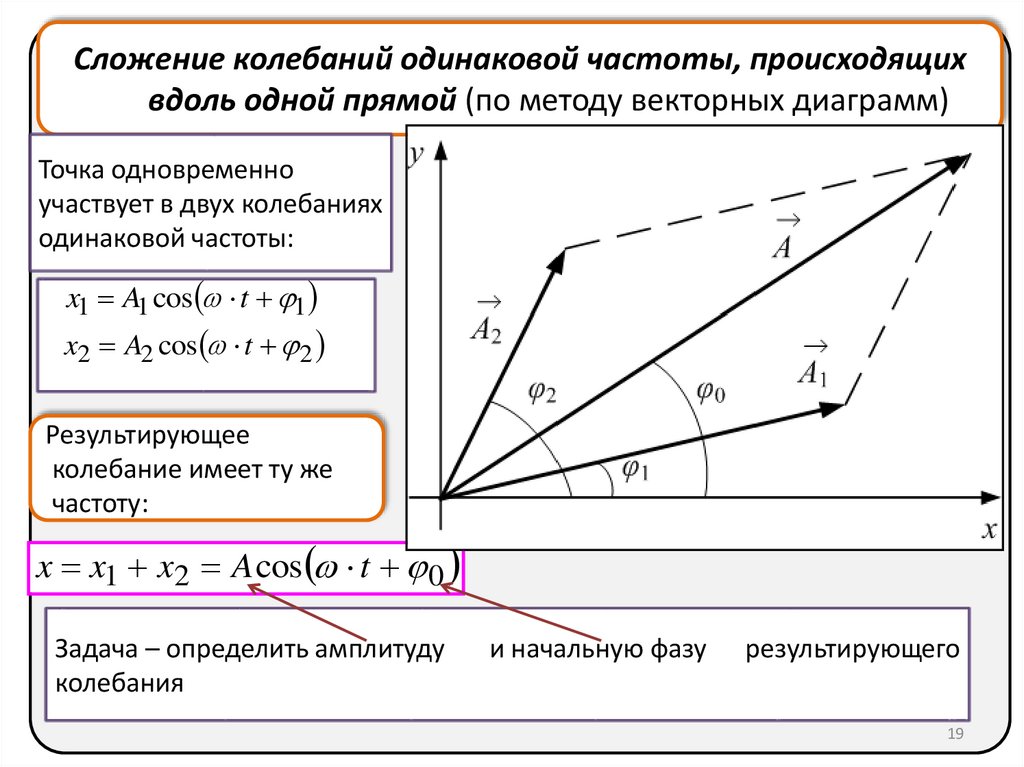
Сложение колебаний одинаковой частоты, происходящих
вдоль одной прямой (по методу векторных диаграмм)
Точка одновременно
участвует в двух колебаниях
одинаковой частоты:
x1 A1 cos t 1
x2 A2 cos t 2
Результирующее
колебание имеет ту же
частоту:
x x1 x2 A cos t 0
Задача – определить амплитуду
колебания
и начальную фазу
результирующего
19

20.

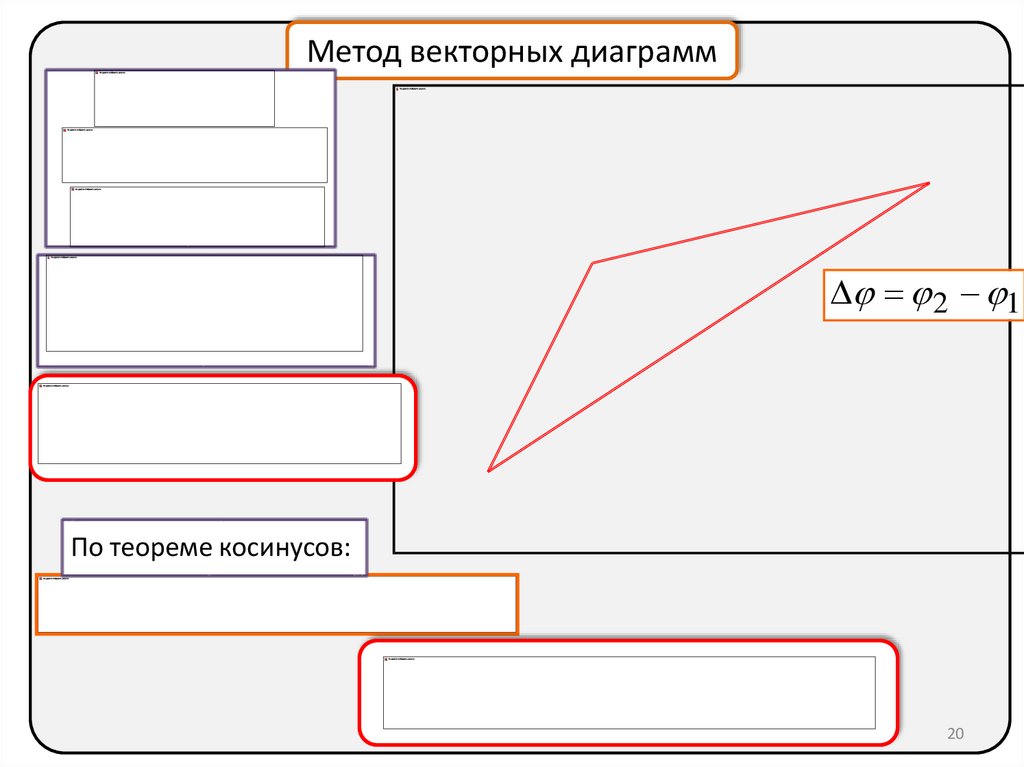
Метод векторных диаграмм
2 1
По теореме косинусов:
20

21.

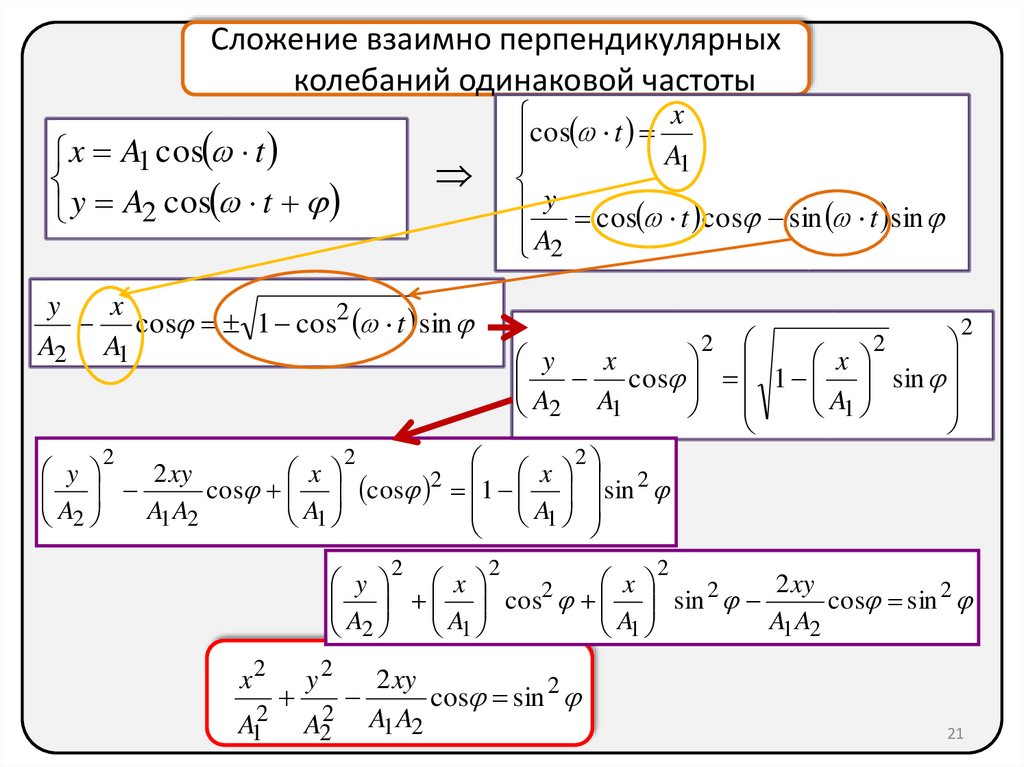
Сложение взаимно перпендикулярных
колебаний одинаковой частоты
x A1 cos t
y A2 cos t
x
cos t A
1
y cos t cos sin t sin
A2
y
x
cos 1 cos2 t sin
A2 A1
y
x
cos
A2 A1
2
2
x
1 sin
A1
2
2
2
x 2
y
x
2 xy
cos cos 2 1 sin 2
A1 A2
A1
A2
A1
2
2
2
y
x
x
2 xy
cos2 sin 2
cos sin 2
A1 A2
A2
A1
A1
x2
A12
y2
A22
2 xy
cos sin 2
A1 A2
21

22.

Сложение взаимно перпендикулярных
колебаний одинаковой частоты
x A1 cos t
y A2 cos t
x2
A12
y2
A22
2 xy
cos sin 2
A1 A2
В общем случае это уравнение эллипса:
22

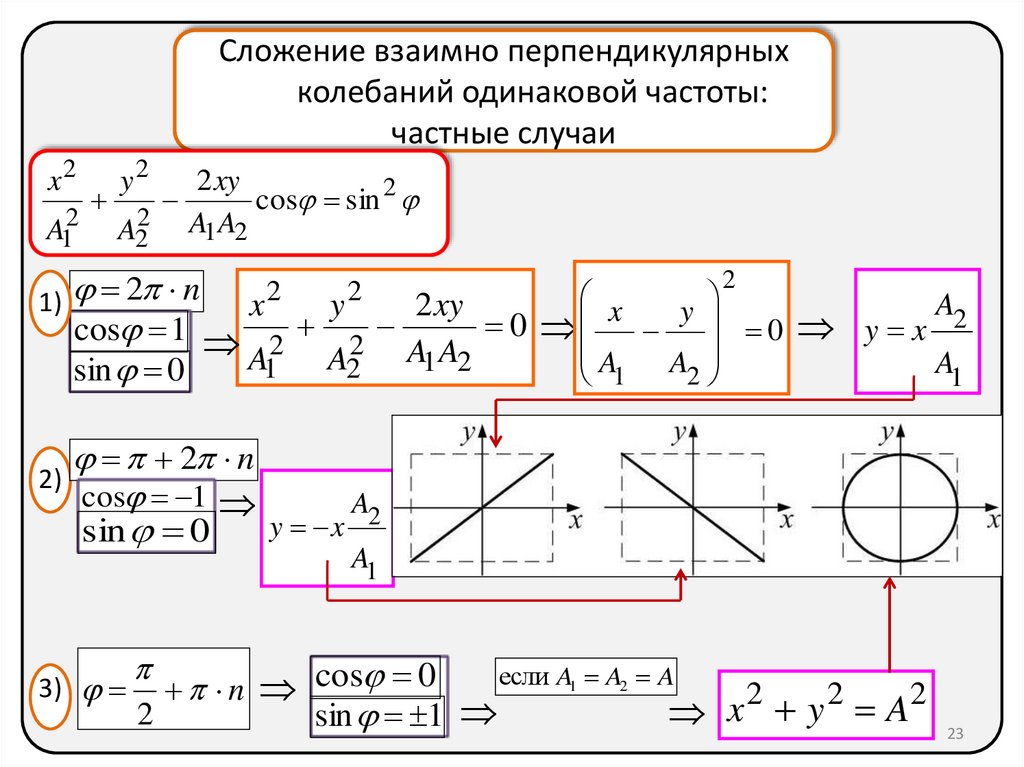
23.

Сложение взаимно перпендикулярных
колебаний одинаковой частоты:
частные случаи
x2
A12
y2
A22
2 xy
cos sin 2
A1 A2
2
2
n
2
2
x
1)
A2
x
y
2 xy
y
0
0 y x
cos 1 2 2
A1 A2 A1 A2
A1
sin 0
A1 A2
2)
2 n
cos 1
sin 0
3)
y x
A2
A1
если A1 A2 A
n cos 0
2
2
2
x
y
A
2
sin 1
23

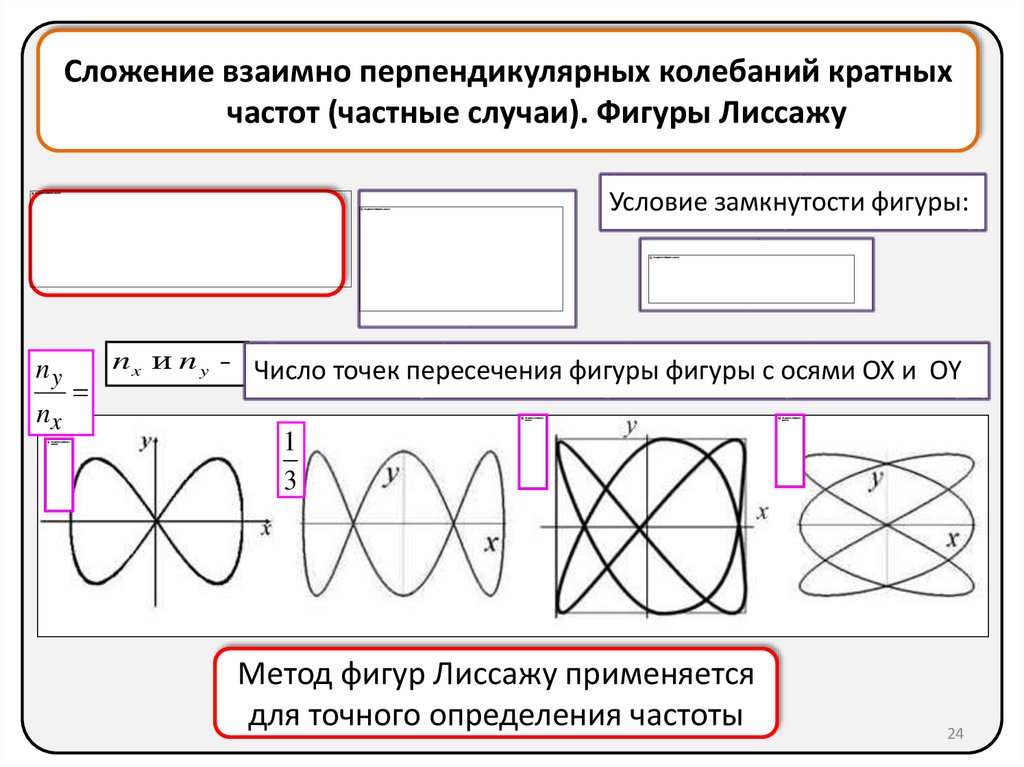
24.

Сложение взаимно перпендикулярных колебаний кратных
частот (частные случаи). Фигуры Лиссажу
Условие замкнутости фигуры:
ny
nx
n x и n y - Число точек пересечения фигуры фигуры с осями OX и OY
1
3
Метод фигур Лиссажу применяется
для точного определения частоты
24

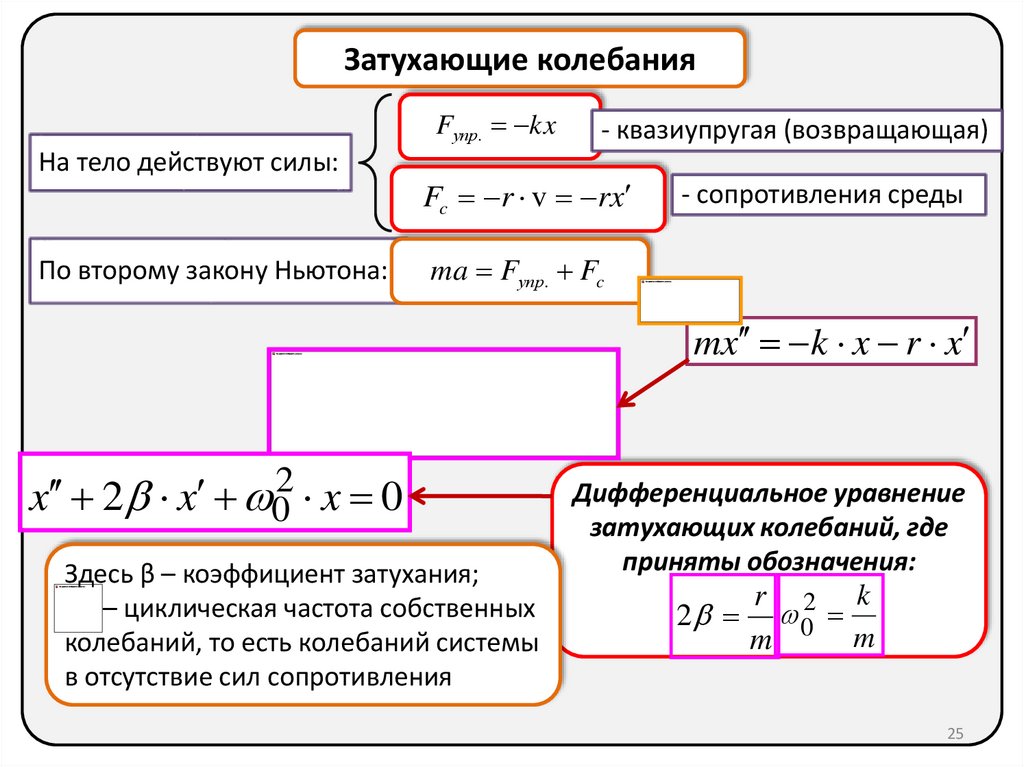
25.

Затухающие колебания
Fупр. kx
На тело действуют силы:
По второму закону Ньютона:
- квазиупругая (возвращающая)
Fc r v rx
- сопротивления среды
ma Fупр. Fc
mx k x r x
x 2 x 02 x 0
Здесь β – коэффициент затухания;
– циклическая частота собственных
колебаний, то есть колебаний системы
в отсутствие сил сопротивления
Дифференциальное уравнение
затухающих колебаний, где
приняты обозначения:
k
r
2 02
m
m
25

26.

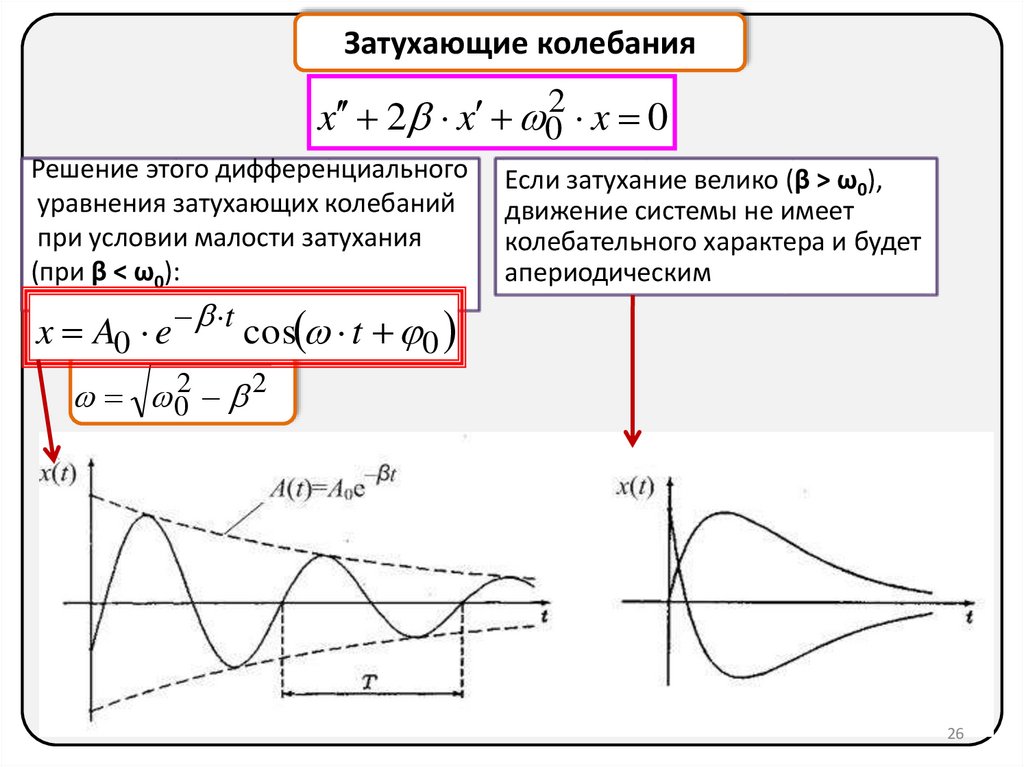
Затухающие колебания
x 2 x 02 x 0
Решение этого дифференциального
уравнения затухающих колебаний
при условии малости затухания
(при β < ω0):
Если затухание велико (β > ω0),
движение системы не имеет
колебательного характера и будет
апериодическим
x A0 e t cos t 0
02 2
26

27.

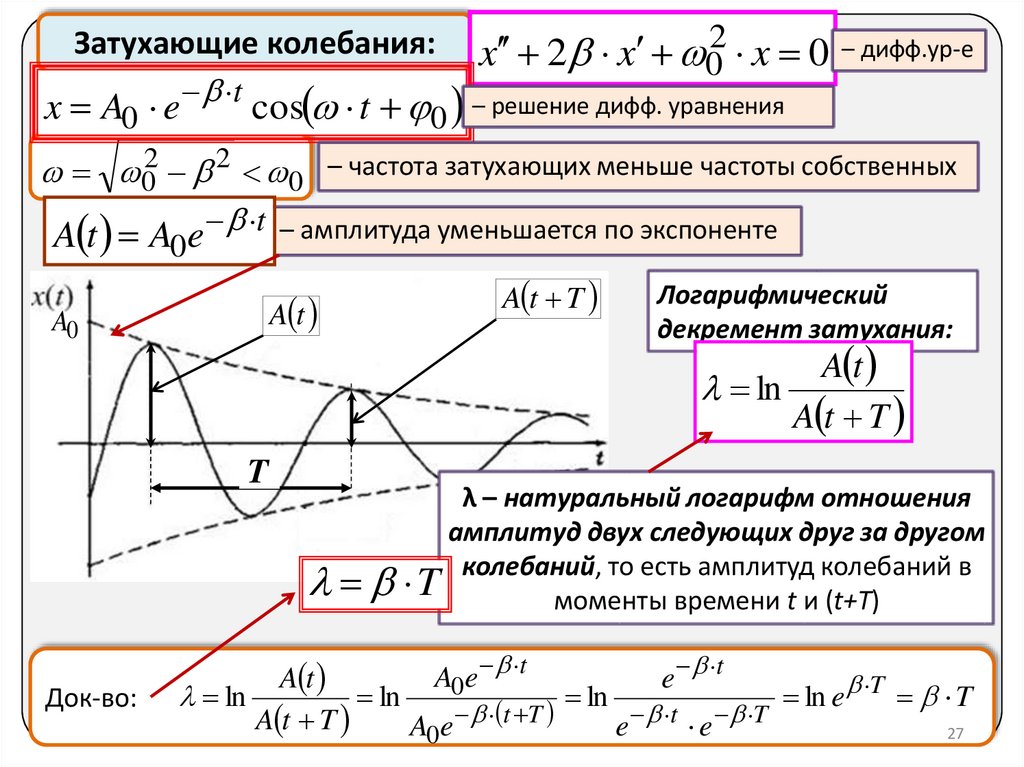
Затухающие колебания: x 2 x 2 x 0 – дифф.ур-е
0
x A e t cos t – решение дифф. уравнения
0
0
02 2 0 – частота затухающих меньше частоты собственных
A t A e t – амплитуда уменьшается по экспоненте
0
A t
A0
T
Док-во:
A t T
Логарифмический
декремент затухания:
A t
ln
A t T
λ – натуральный логарифм отношения
амплитуд двух следующих друг за другом
то есть амплитуд колебаний в
T колебаний,
моменты времени t и (t+T)
A0e t
A t
e t
ln
ln
ln
ln e T T
A t T
A0e t T
e t e T
27

28.

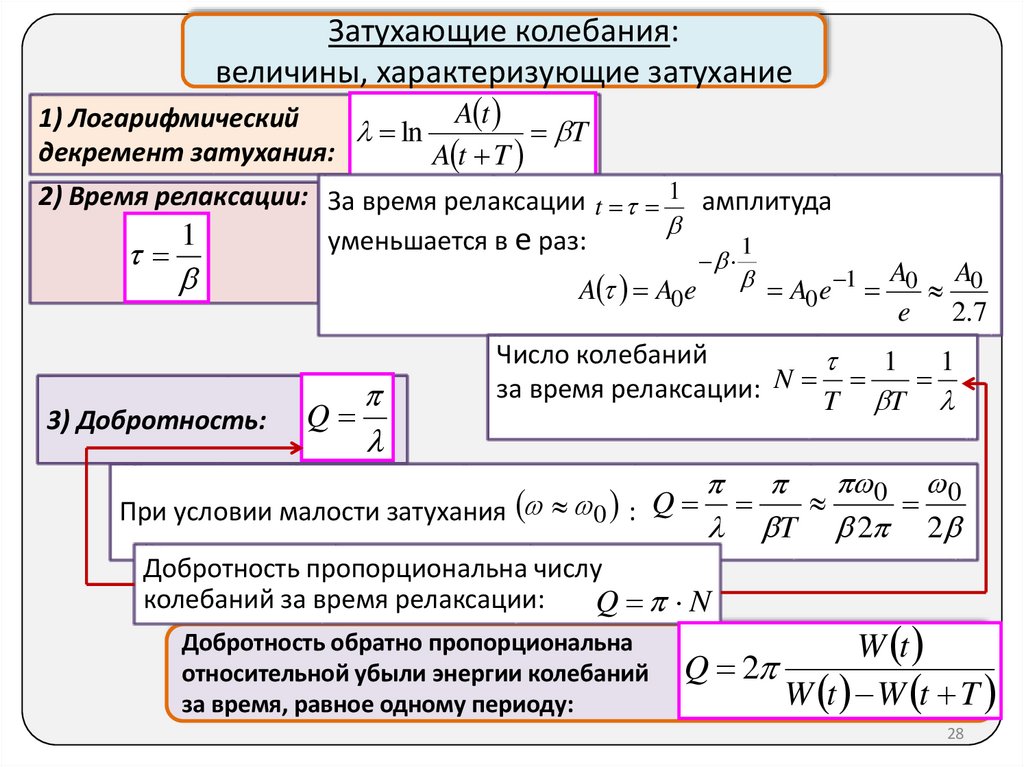
Затухающие колебания:
величины, характеризующие затухание
A t
1) Логарифмический
ln
T
декремент затухания:
A t T
2) Время релаксации: За время релаксации t 1 амплитуда
1
уменьшается в е раз:
1
3) Добротность:
A A0e
Q
A e 1 A0 A0
0
e
2.7
Число колебаний
1
1
N
за время релаксации:
T T
0 0
При условии малости затухания 0 : Q
T 2 2
Добротность пропорциональна числу
колебаний за время релаксации:
Q N
Добротность обратно пропорциональна
относительной убыли энергии колебаний
за время, равное одному периоду:
W t
Q 2
W t W t T
28

29.

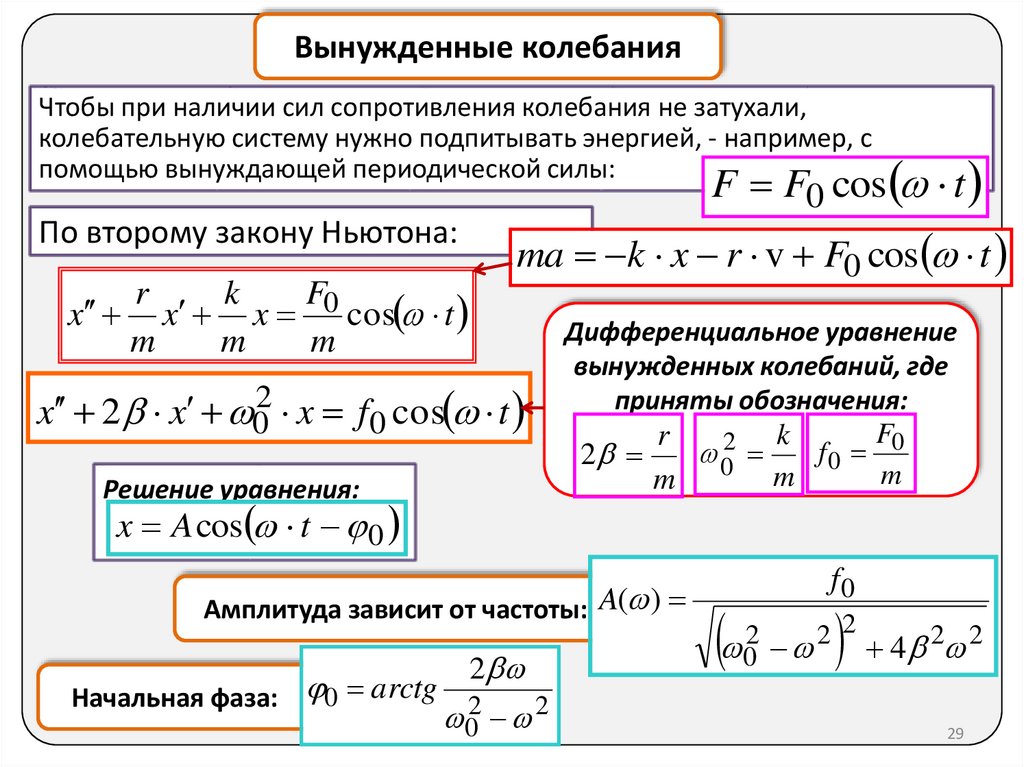
Вынужденные колебания
Чтобы при наличии сил сопротивления колебания не затухали,
колебательную систему нужно подпитывать энергией, - например, с
помощью вынуждающей периодической силы:
F F0 cos t
По второму закону Ньютона:
x
r
k
F0
x x cos t
m
m
m
ma k x r v F0 cos t
x 2 x 02 x f0 cos t
Решение уравнения:
x A cos t 0
Дифференциальное уравнение
вынужденных колебаний, где
приняты обозначения:
F0
k
r
2
f0
0
2
m
m
m
Амплитуда зависит от частоты: A( )
2
arctg
0
Начальная фаза:
02 2
f0
2
2 2
0
4 2 2
29

30.

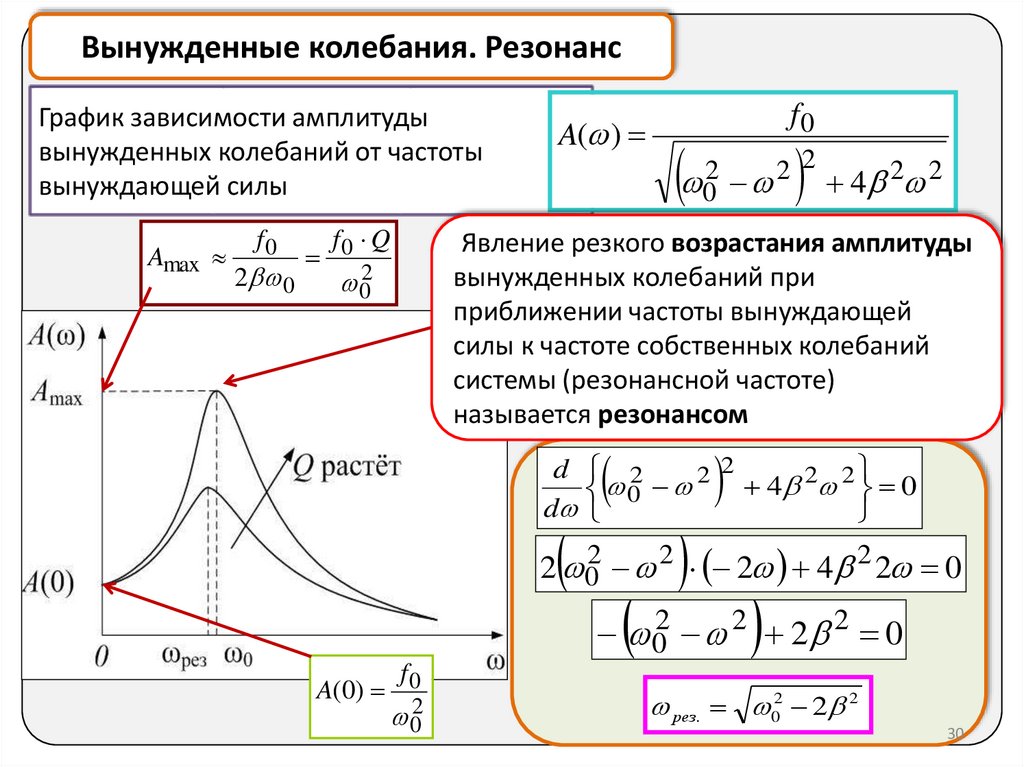
Вынужденные колебания. Резонанс
График зависимости амплитуды
вынужденных колебаний от частоты
вынуждающей силы
Amax
f0
2 0
f Q
0
A( )
f0
2
2 2
0
4 2 2
Явление резкого возрастания амплитуды
вынужденных колебаний при
приближении частоты вынуждающей
силы к частоте собственных колебаний
системы (резонансной частоте)
называется резонансом
02
d 2
2 2
4 2 2 0
0
d
2 02 2 2 4 2 2 0
02 2 2 2 0
f
A(0) 0
02
рез. 02 2 2
30

31.

По этим ссылкам можно посмотреть видео
http://www.youtube.com/watch?v=093CzGsstv0 – свободные и
вынужденные колебания, резонанс
http://www.youtube.com/watch?v=BAyt7KVtG58 – вынужденные
колебания, резонанс
http://youtu.be/rdWWvjH8cPM - фигуры Лиссажу
31

32.

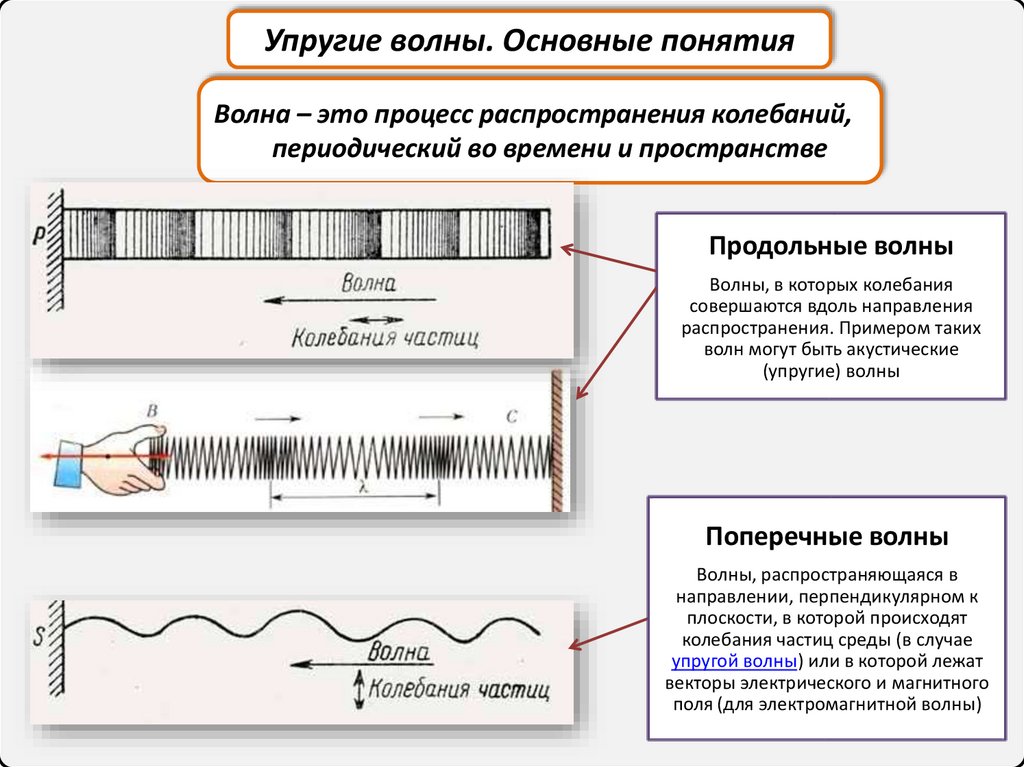
Упругие волны. Основные понятия
Волна – это процесс распространения колебаний,
периодический во времени и пространстве
Продольные волны
Волны, в которых колебания
совершаются вдоль направления
распространения. Примером таких
волн могут быть акустические
(упругие) волны
Поперечные волны
Волны, распространяющаяся в
направлении, перпендикулярном к
плоскости, в которой происходят
колебания частиц среды (в случае
упругой волны) или в которой лежат
векторы электрического и магнитного
поля (для электромагнитной волны)
32

33.

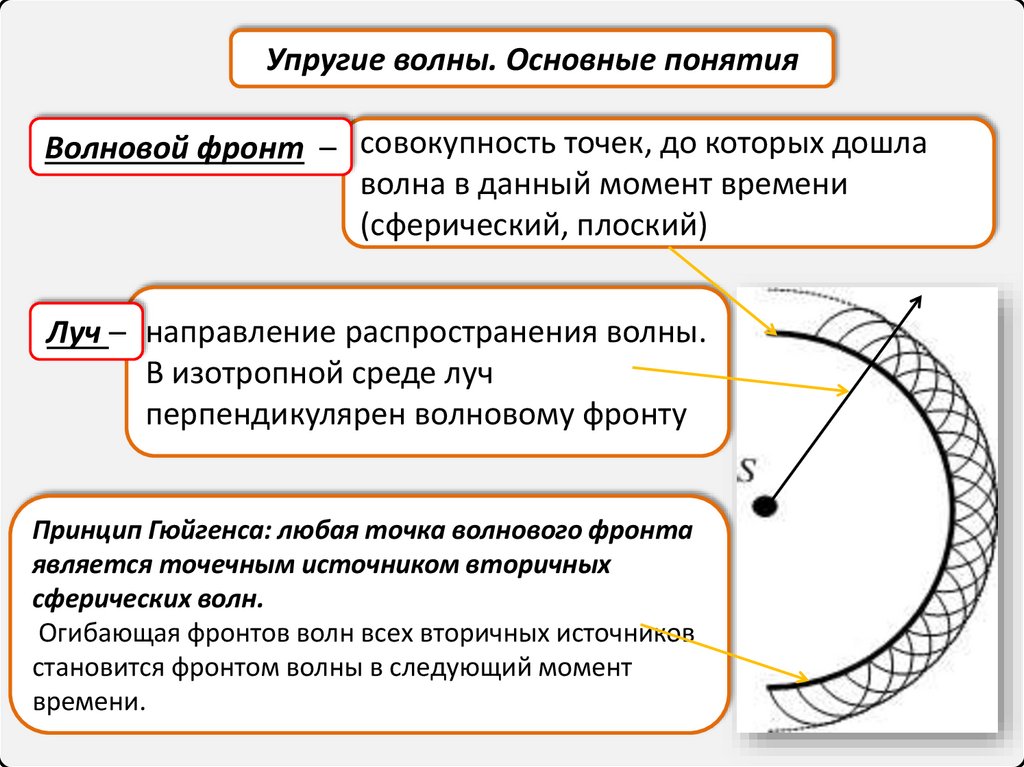
Упругие волны. Основные понятия
Волновой фронт – совокупность точек, до которых дошла
волна в данный момент времени
(сферический, плоский)
Луч – направление распространения волны.
В изотропной среде луч
перпендикулярен волновому фронту
Принцип Гюйгенса: любая точка волнового фронта
является точечным источником вторичных
сферических волн.
Огибающая фронтов волн всех вторичных источников
становится фронтом волны в следующий момент
времени.

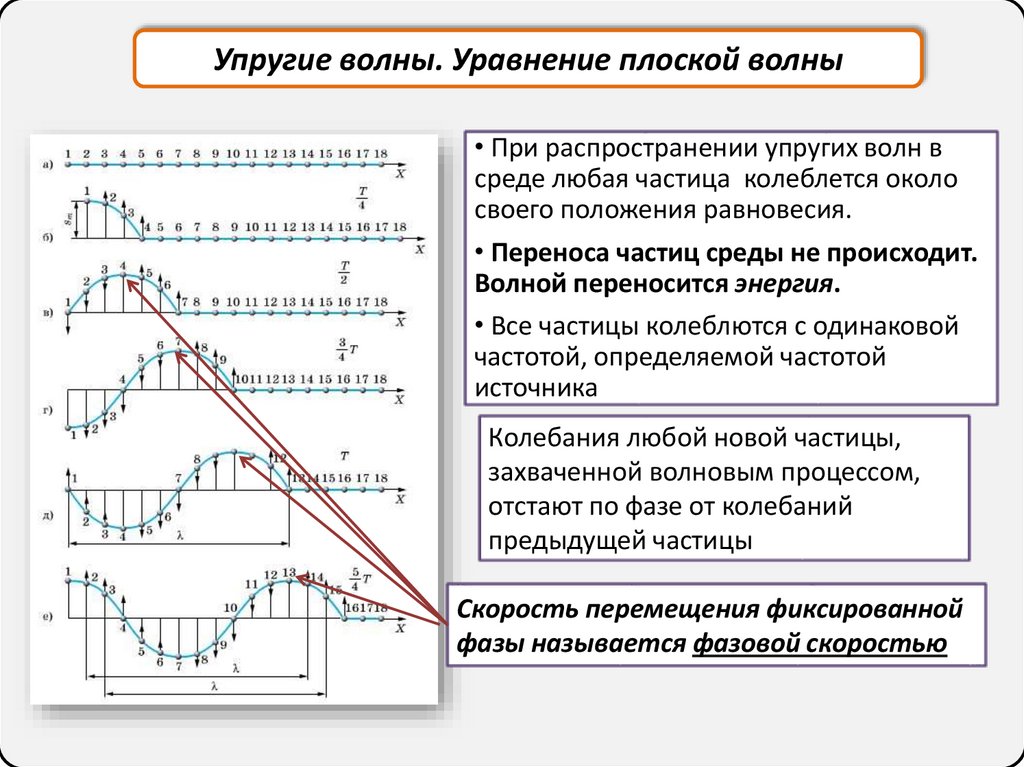
34.

Упругие волны. Уравнение плоской волны
• При распространении упругих волн в
среде любая частица колеблется около
своего положения равновесия.
• Переноса частиц среды не происходит.
Волной переносится энергия.
• Все частицы колеблются с одинаковой
частотой, определяемой частотой
источника
Колебания любой новой частицы,
захваченной волновым процессом,
отстают по фазе от колебаний
предыдущей частицы
Скорость перемещения фиксированной
фазы называется фазовой скоростью

35.

35

36.

36

37.

37

38.

38

39.

Уравнение плоской волны
Уравнение колебаний источника в
точке x=0:
S A cos t
В произвольной точке x
колебания запаздывают по фазе
x
– время запаздывания (за это время волна дойдёт до точки x)
v
Замена t t
даёт уравнение колебаний в точке x:
x
S x, t A cos t
v
x
S x, t A cos t
v
S x, t A cos t x
v

40.

Уравнение плоской волны
S x, t A cos t x
v
Функция двух переменных: x и t
k
v
S x, t A cos t k x
k - Волновое число
Волновой вектор — вектор, направление которого перпендикулярно
фронту волны, а абсолютное значение равно волновому числу.
Длина волны: v T
k
v
2
2
T v

41.

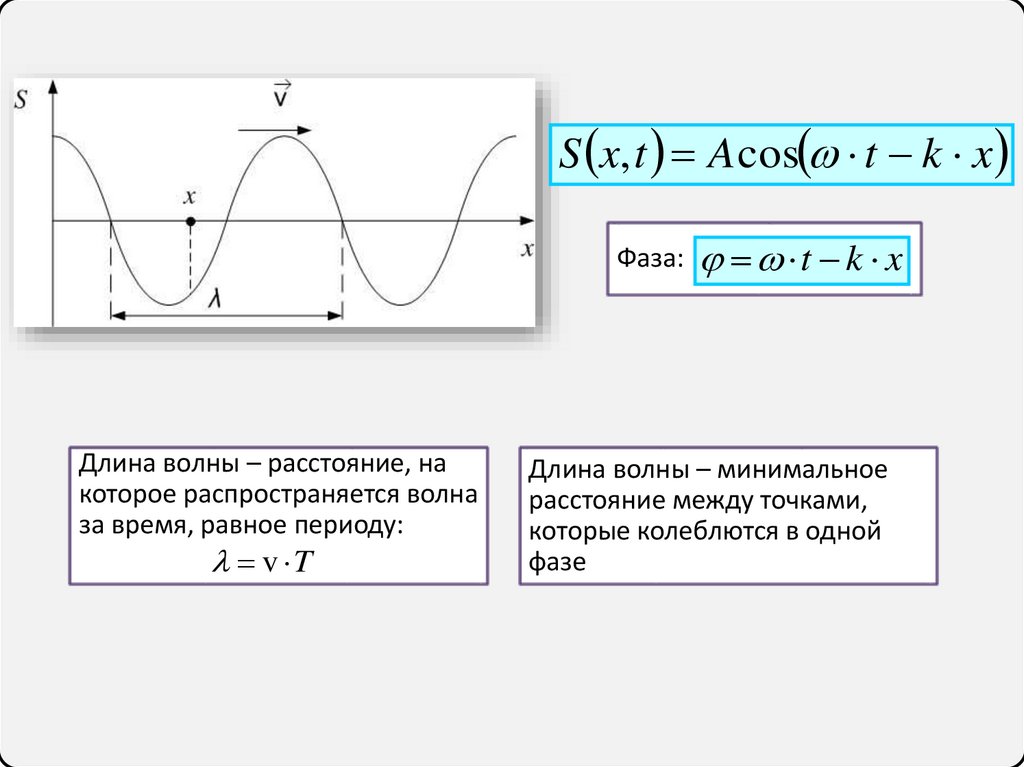
S x, t A cos t k x
Фаза: t k x
Длина волны – расстояние, на
которое распространяется волна
за время, равное периоду:
v T
Длина волны – минимальное
расстояние между точками,
которые колеблются в одной
фазе

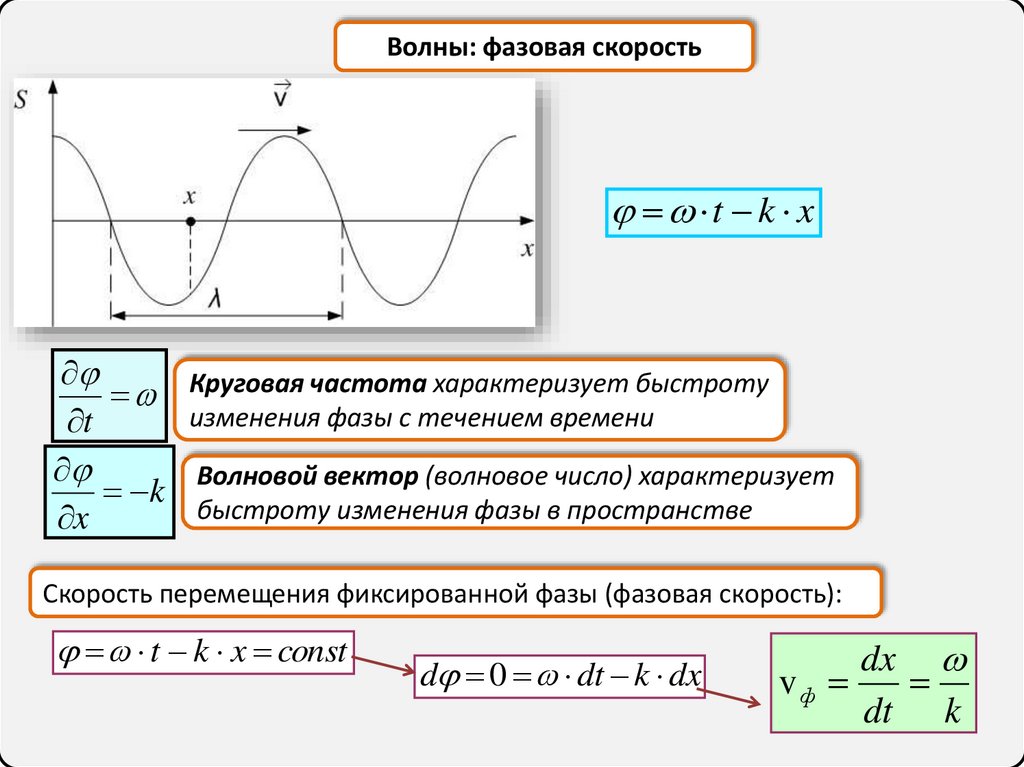
42.

Волны: фазовая скорость
t k x
t
k
x
Круговая частота характеризует быстроту
изменения фазы с течением времени
Волновой вектор (волновое число) характеризует
быстроту изменения фазы в пространстве
Скорость перемещения фиксированной фазы (фазовая скорость):
t k x const
d 0 dt k dx
dx
vф
dt k

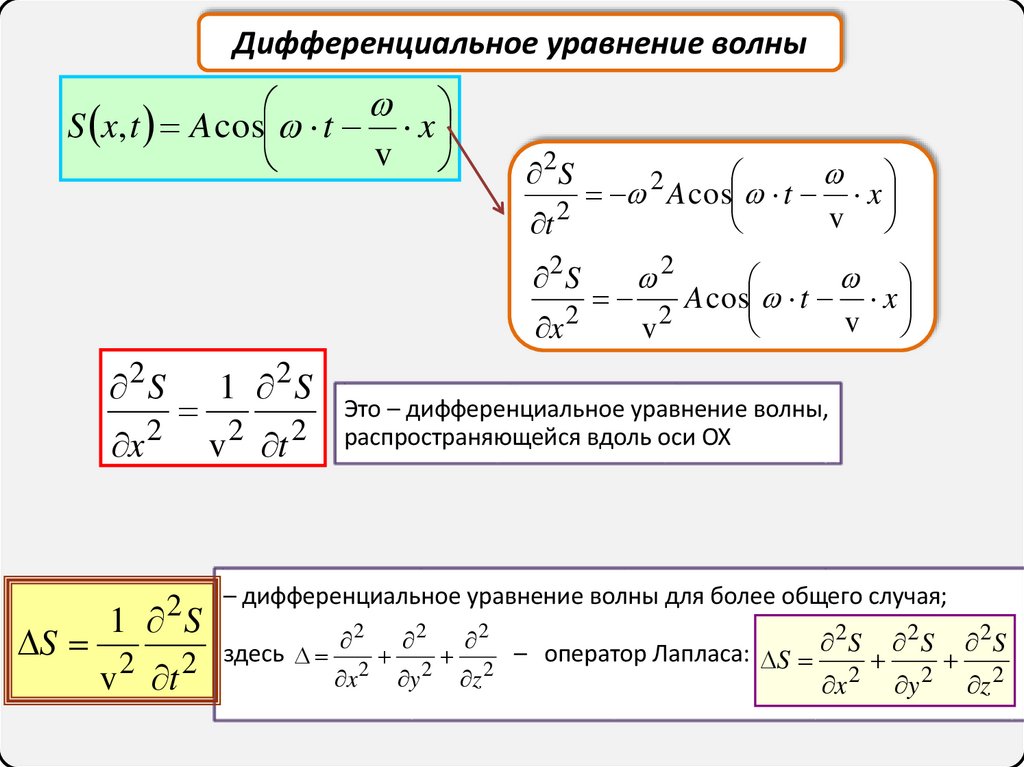
43.

Дифференциальное уравнение волны
S x, t A cos t x
v
2 A cos t x
v
t 2
2S
A cos t x
2
2
v
x
v
2S
2S
x 2
S
2
1 S
2
v t
1 2S
v 2 t 2
2
Это – дифференциальное уравнение волны,
распространяющейся вдоль оси OX
– дифференциальное уравнение волны для более общего случая;
2
2
2
2 здесь x 2 y 2 z 2 – оператор Лапласа: S
2S
x
2
2S
y
2
2S
z 2

44.

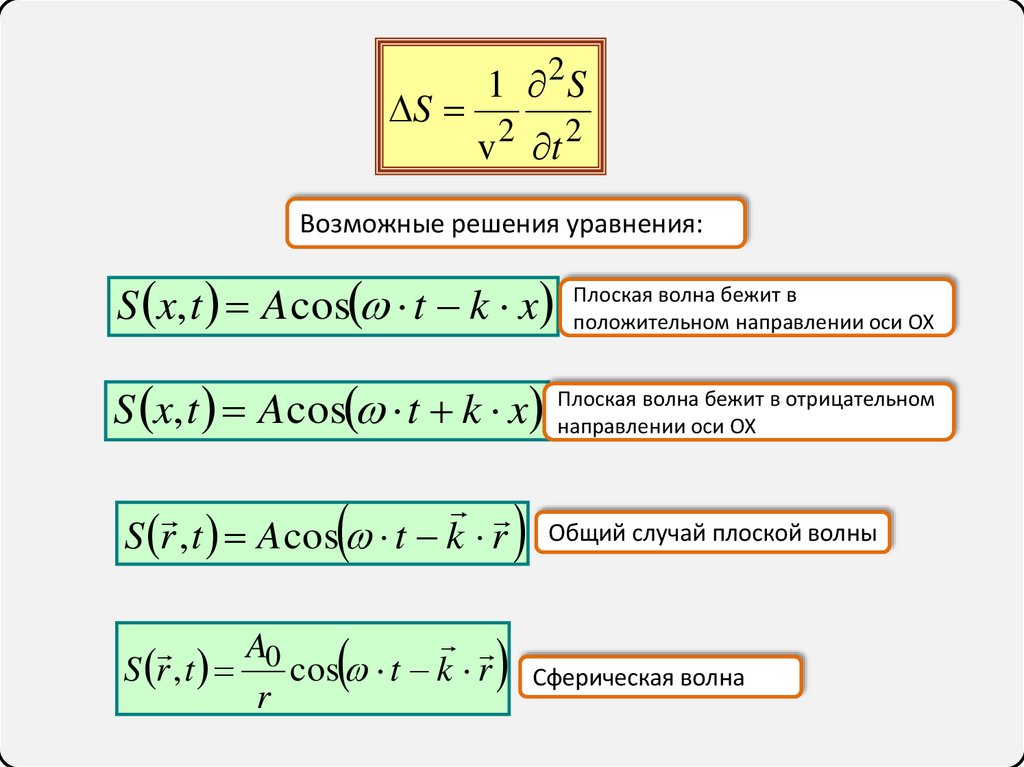
S
1 2S
v 2 t 2
Возможные решения уравнения:
волна бежит в
S x, t A cos t k x Плоская
положительном направлении оси OX
волна бежит в отрицательном
S x, t A cos t k x Плоская
направлении оси OX
Сферическая волна
S r , t A cos t k r
A0
S r , t
cos t k r
r
Общий случай плоской волны

45.

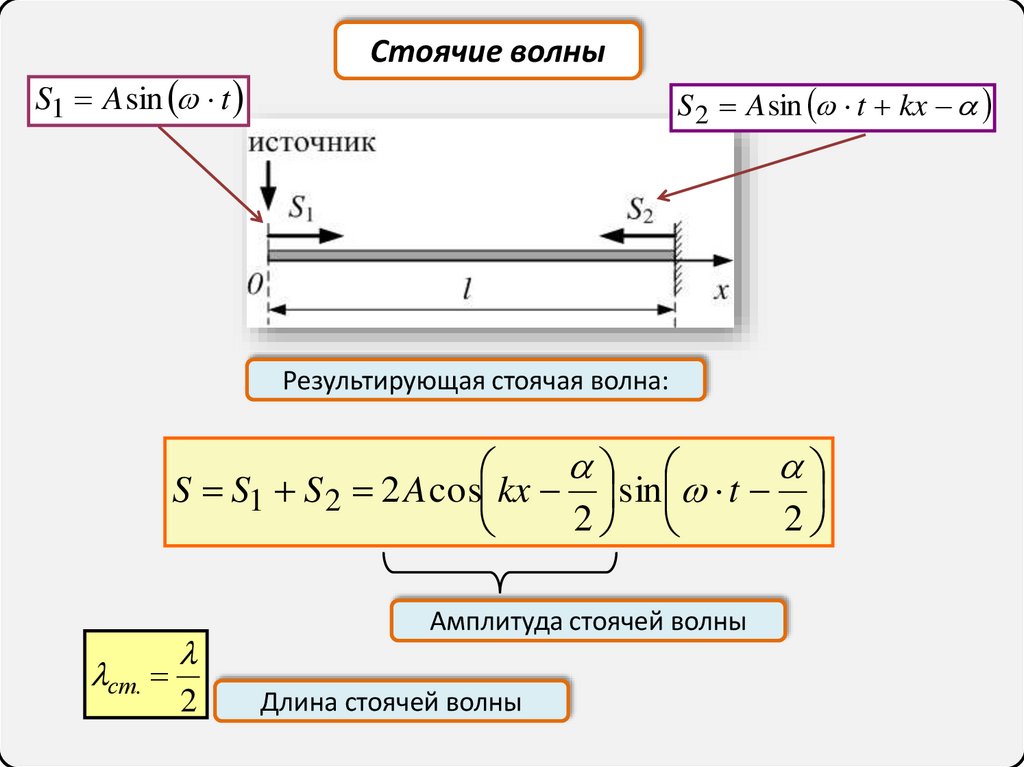
S1 A sin t
Стоячие волны
S 2 A sin t kx
Результирующая стоячая волна:
S S1 S 2 2 A cos kx sin t
2
2
ст.
2
Амплитуда стоячей волны
Длина стоячей волны

46.

46

47.

47

48.

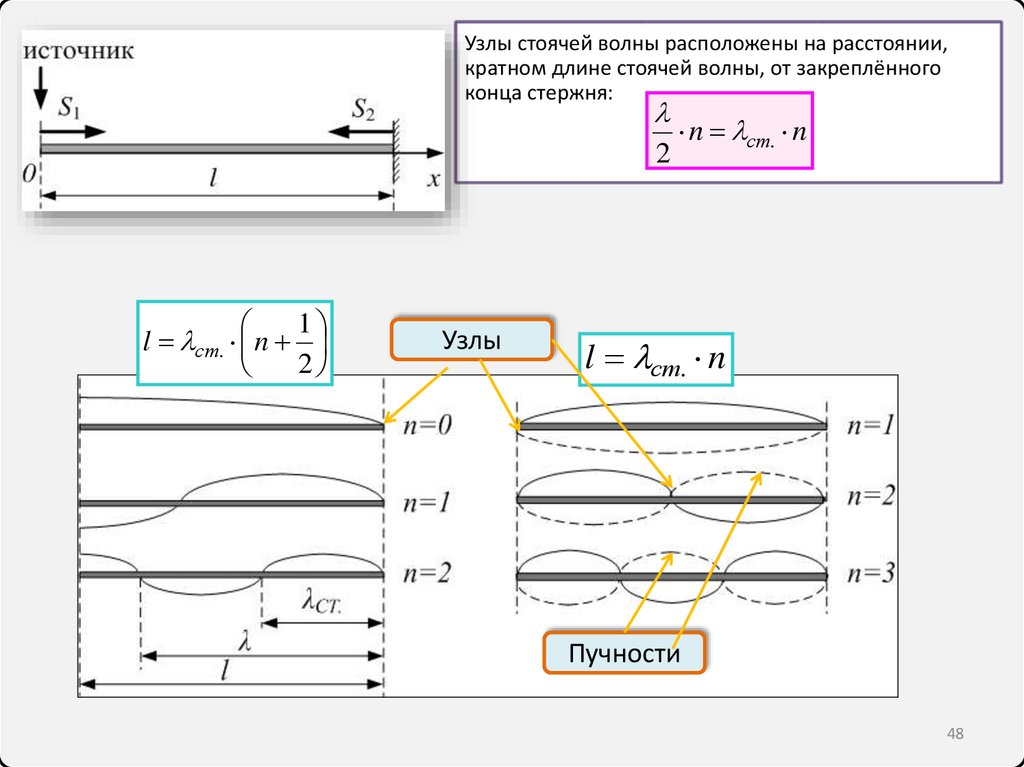
Узлы стоячей волны расположены на расстоянии,
кратном длине стоячей волны, от закреплённого
конца стержня:
2
1
l ст. n
2
Узлы
n ст. n
l ст. n
Пучности
48

49.

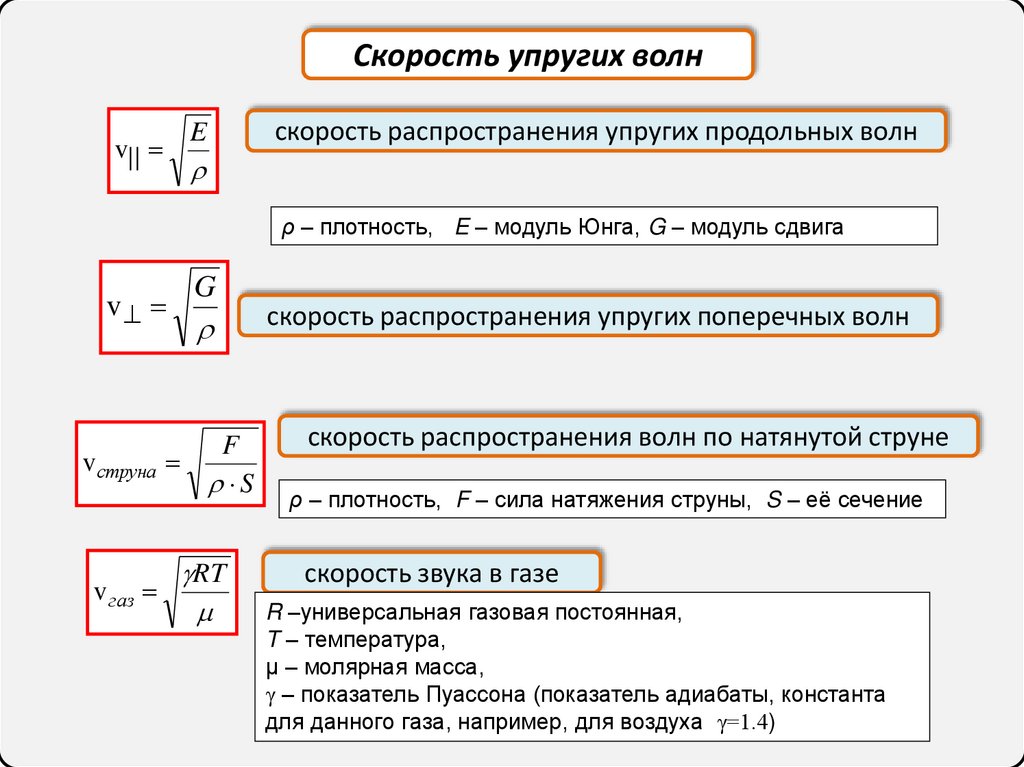
Скорость упругих волн
v| |
E
скорость распространения упругих продольных волн
ρ – плотность, E – модуль Юнга, G – модуль сдвига
v
G
F
vструна
S
v газ
RT
скорость распространения упругих поперечных волн
скорость распространения волн по натянутой струне
ρ – плотность, F – сила натяжения струны, S – её сечение
скорость звука в газе
R –универсальная газовая постоянная,
T – температура,
μ – молярная масса,
γ – показатель Пуассона (показатель адиабаты, константа
для данного газа, например, для воздуха γ=1.4)

50.

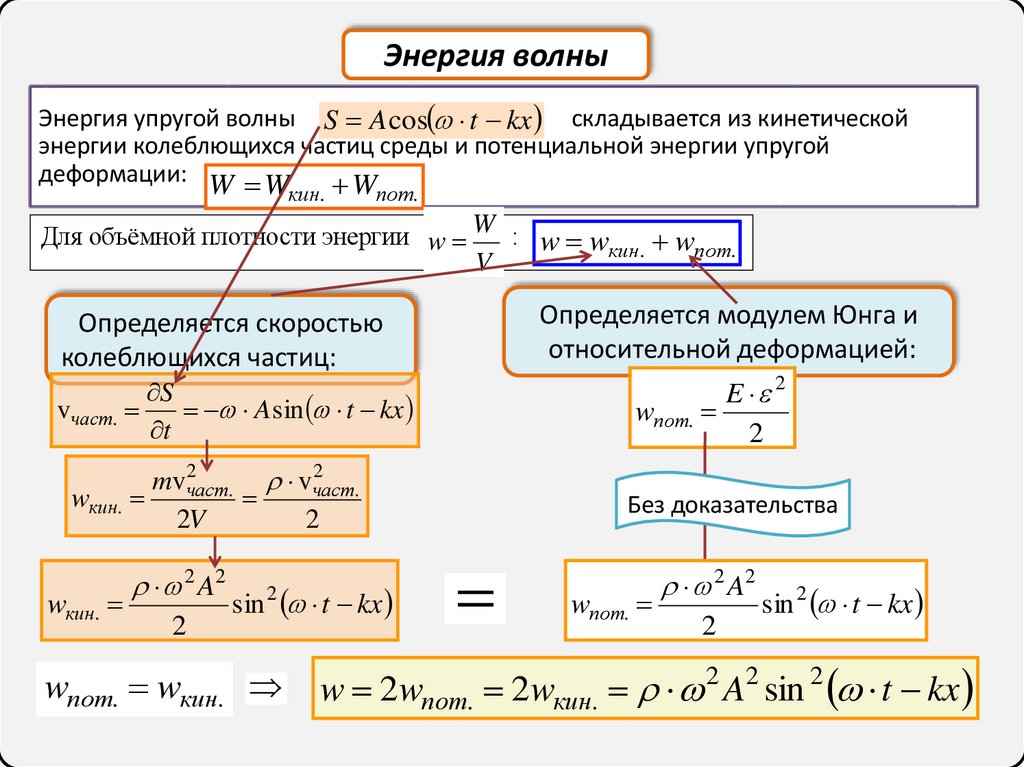
Энергия волны
Энергия упругой волны S A cos t kx складывается из кинетической
энергии колеблющихся частиц среды и потенциальной энергии упругой
деформации: W W
W
кин.
пот.
Для объёмной плотности энергии w W : w wкин. wпот.
V
Определяется модулем Юнга и
относительной деформацией:
Определяется скоростью
колеблющихся частиц:
E 2
wпот.
2
S
vчаст.
A sin t kx
t
2
2
mvчаст
v
.
част.
wкин.
2V
2
wкин.
2 A2
2
sin t kx
2
wпот. wкин.
Без доказательства
wпот.
2 A2
2
sin 2 t kx
w 2wпот. 2wкин. 2 A2 sin 2 t kx

51.

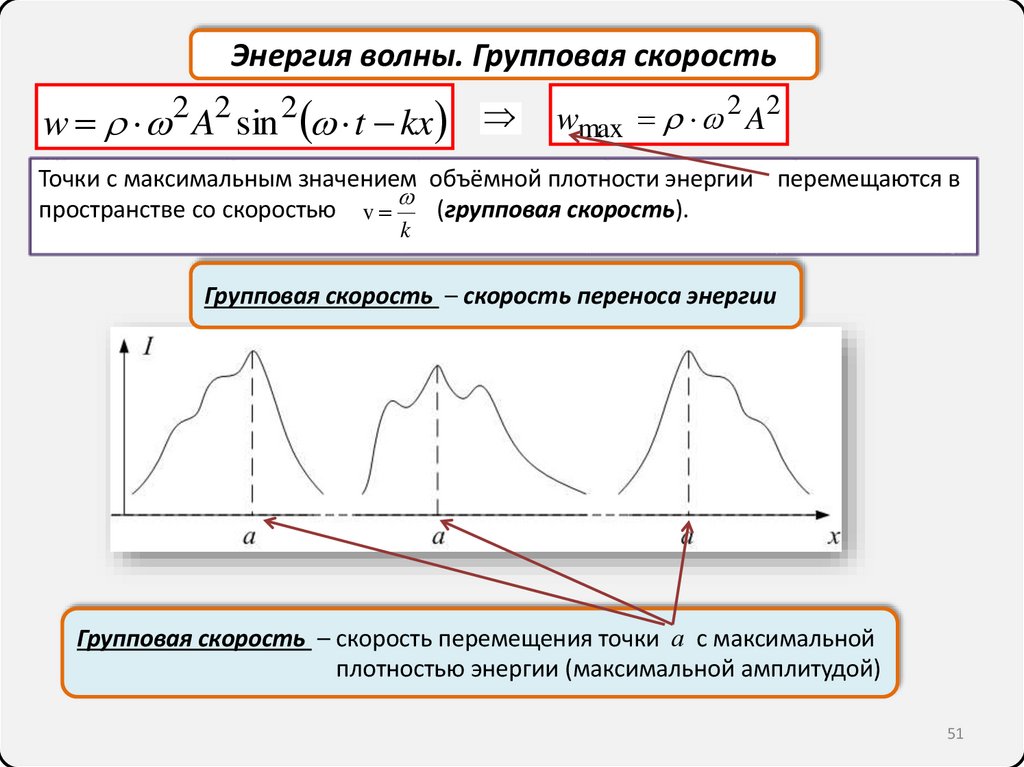
Энергия волны. Групповая скорость
w 2 A2 sin 2 t kx
wmax 2 A2
Точки с максимальным значением объёмной плотности энергии перемещаются в
пространстве со скоростью v (групповая скорость).
k
Групповая скорость – скорость переноса энергии
Групповая скорость – скорость перемещения точки а с максимальной
плотностью энергии (максимальной амплитудой)
51

52.

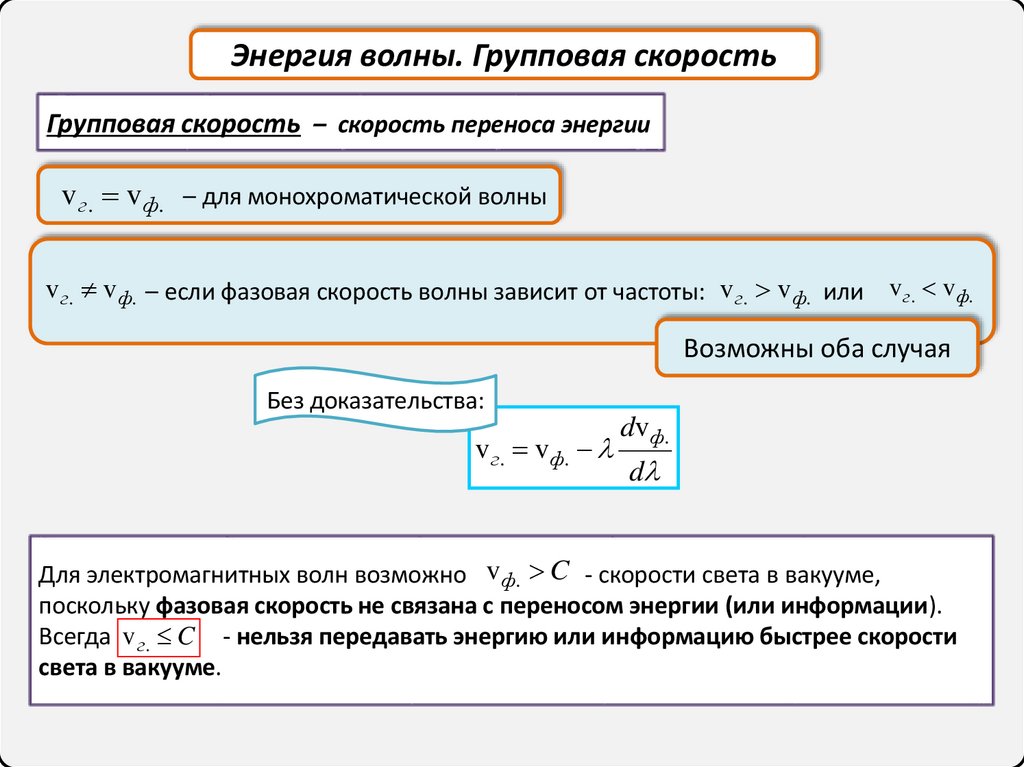
Энергия волны. Групповая скорость
Групповая скорость – скорость переноса энергии
v г. vф. – для монохроматической волны
v г. vф. – если фазовая скорость волны зависит от частоты: v г. vф. или v г. vф.
Возможны оба случая
Без доказательства:
v г. vф.
dvф.
d
Для электромагнитных волн возможно vф. C - скорости света в вакууме,
поскольку фазовая скорость не связана с переносом энергии (или информации).
Всегда v г. C - нельзя передавать энергию или информацию быстрее скорости
света в вакууме.

53.

Вектор плотности потока энергии
(вектор Умова). Интенсивность волны
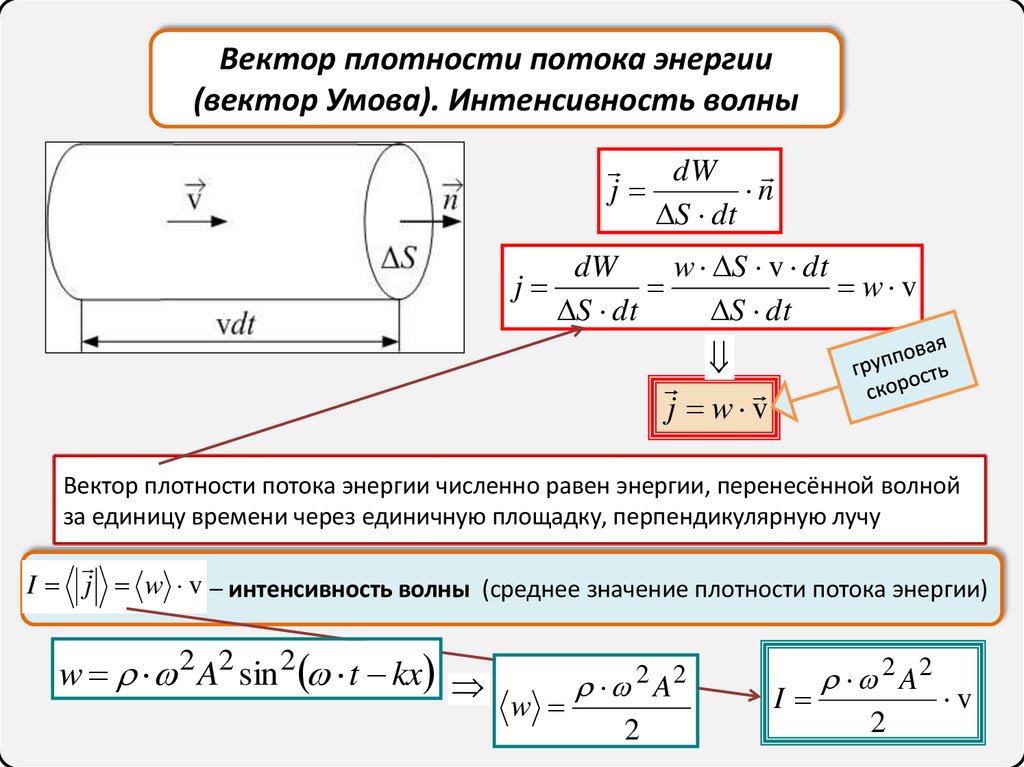
dW
j
n
S dt
dW
w S v dt
j
w v
S dt
S dt
j w v
Вектор плотности потока энергии численно равен энергии, перенесённой волной
за единицу времени через единичную площадку, перпендикулярную лучу
I j w v – интенсивность волны (среднее значение плотности потока энергии)
w 2 A2 sin 2 t kx
w
A
2 2
2
I
2 A2
2
v

54.

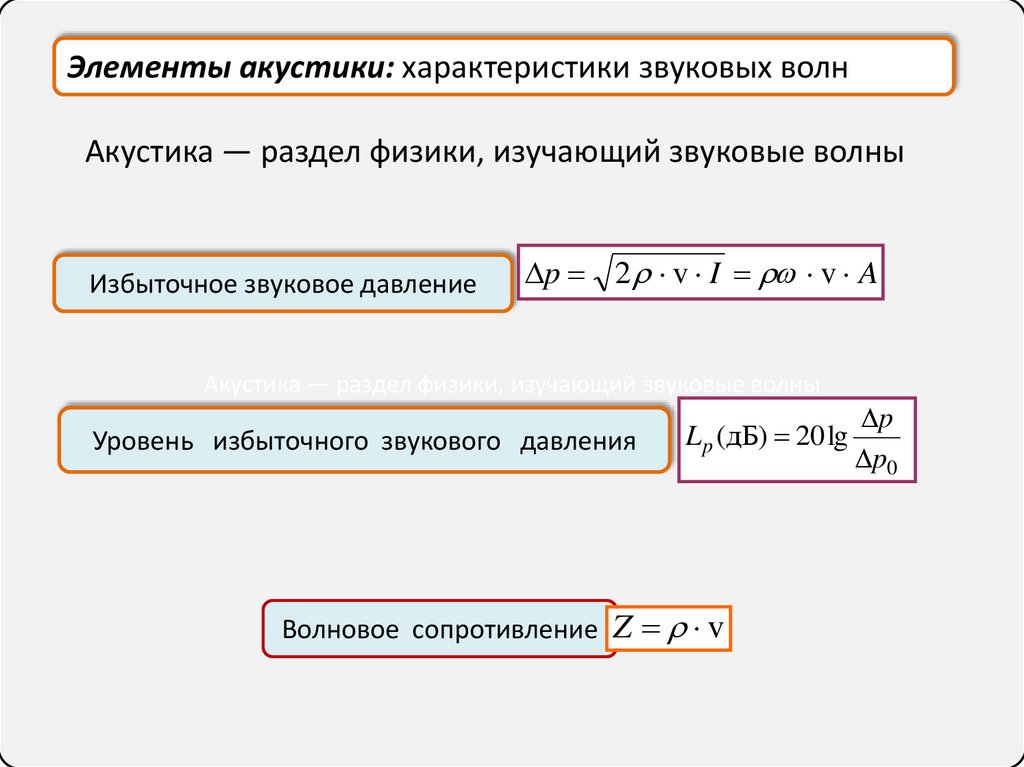
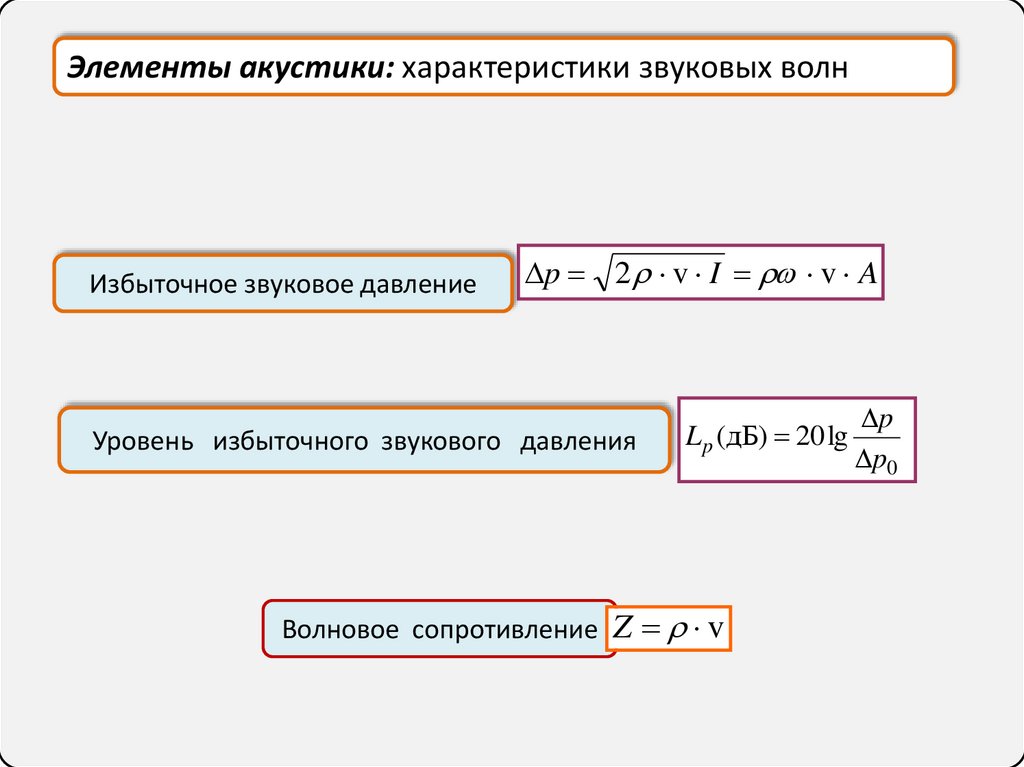
Элементы акустики: характеристики звуковых волн
Акустика — раздел физики, изучающий звуковые волны
Избыточное звуковое давление
p 2 v I v A
Акустика — раздел физики, изучающий звуковые волны
Уровень избыточного звукового давления
L p (дБ) 20 lg
Волновое сопротивление Z v
p
p0

55.

Акустика — раздел физики, изучающий звуковые волны
Звук — физическое явление, представляющее собой распространение
упругих волн в газообразной, жидкой или твёрдой среде.
55

56.

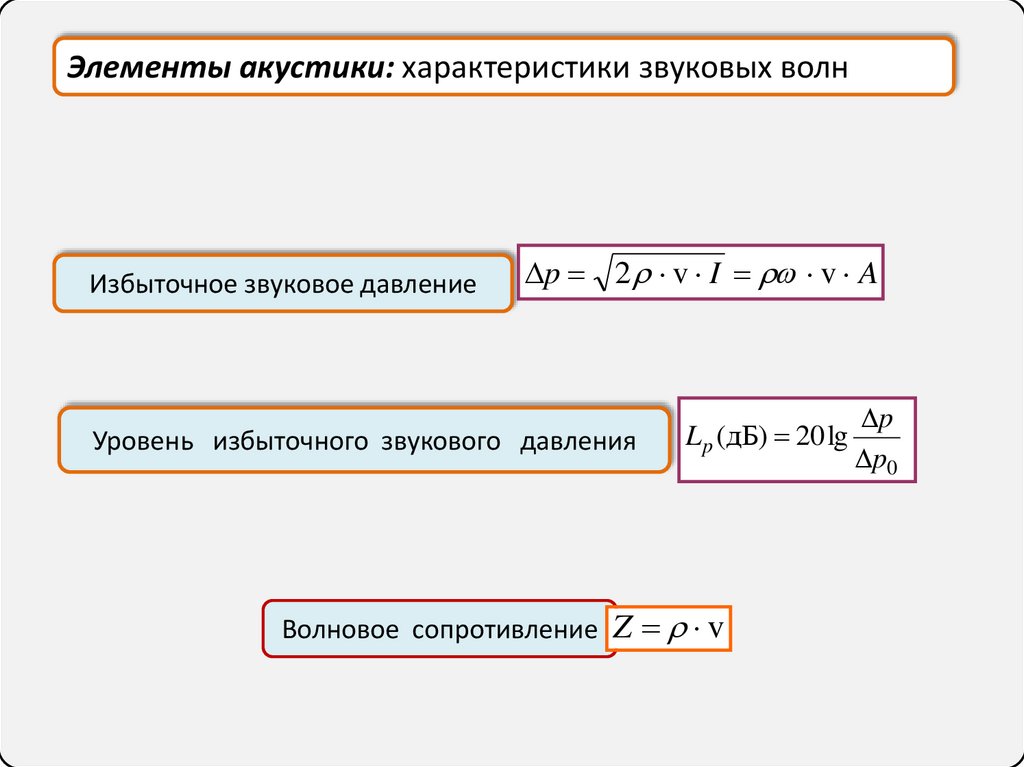
Элементы акустики: характеристики звуковых волн
Избыточное звуковое давление
p 2 v I v A
Уровень избыточного звукового давления
L p (дБ) 20 lg
Волновое сопротивление Z v
p
p0

57.

Звуковые волны
Акустика — раздел физики, изучающий звуковые волны
Звук — физическое явление, распространения упругих волн (в газообразной,
жидкой или твёрдой среде), которые, воздействуя на слуховой аппарат
человека, вызывают определенные (слуховые) ощущения.
,.
Уровень избыточного звукового давления
Волновое сопротивление
L p (дБ) 20 lg
Z v
p
p0

58.

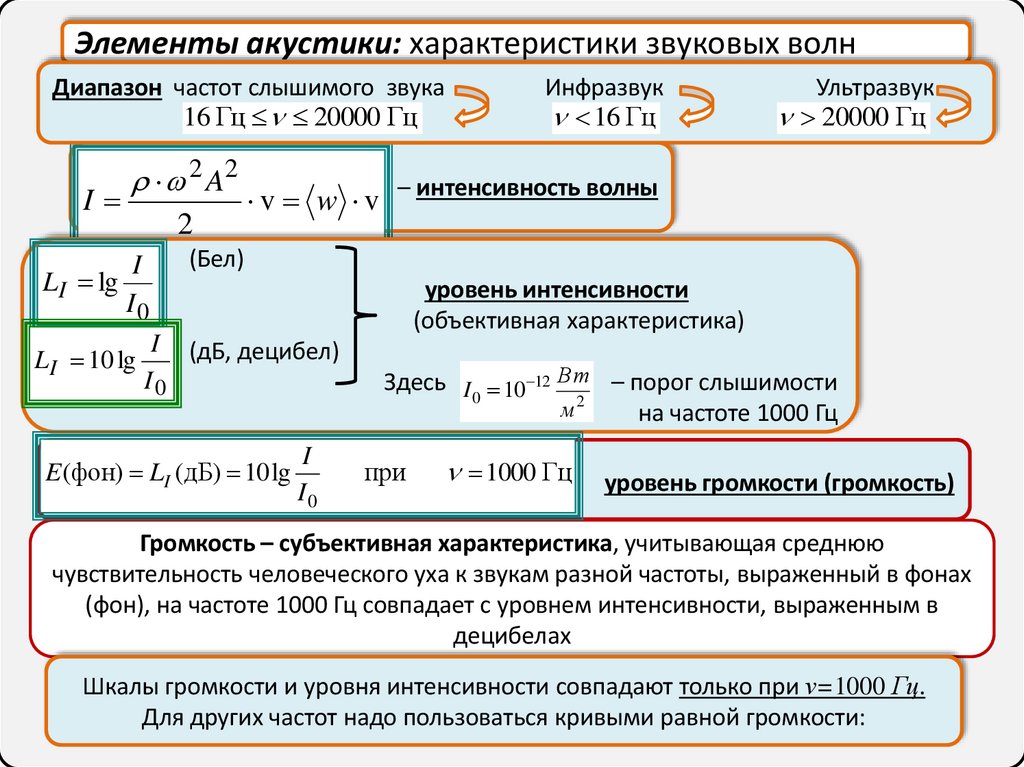
Элементы акустики: характеристики звуковых волн
Диапазон частот слышимого звука
16 Гц 20000 Гц
I
2 A2
2
I
LI lg
I0
LI 10 lg
Инфразвук
16 Гц
Ультразвук
20000 Гц
v w v – интенсивность волны
(Бел)
I (дБ, децибел)
I0
E (фон) LI (дБ) 10 lg
I
I0
уровень интенсивности
(объективная характеристика)
Здесь I 0 10 12 Вт – порог слышимости
м2
на частоте 1000 Гц
при
1000 Гц
уровень громкости (громкость)
Громкость – субъективная характеристика, учитывающая среднюю
чувствительность человеческого уха к звукам разной частоты, выраженный в фонах
(фон), на частоте 1000 Гц совпадает с уровнем интенсивности, выраженным в
децибелах
Шкалы громкости и уровня интенсивности совпадают только при ν=1000 Гц.
Для других частот надо пользоваться кривыми равной громкости:

59.

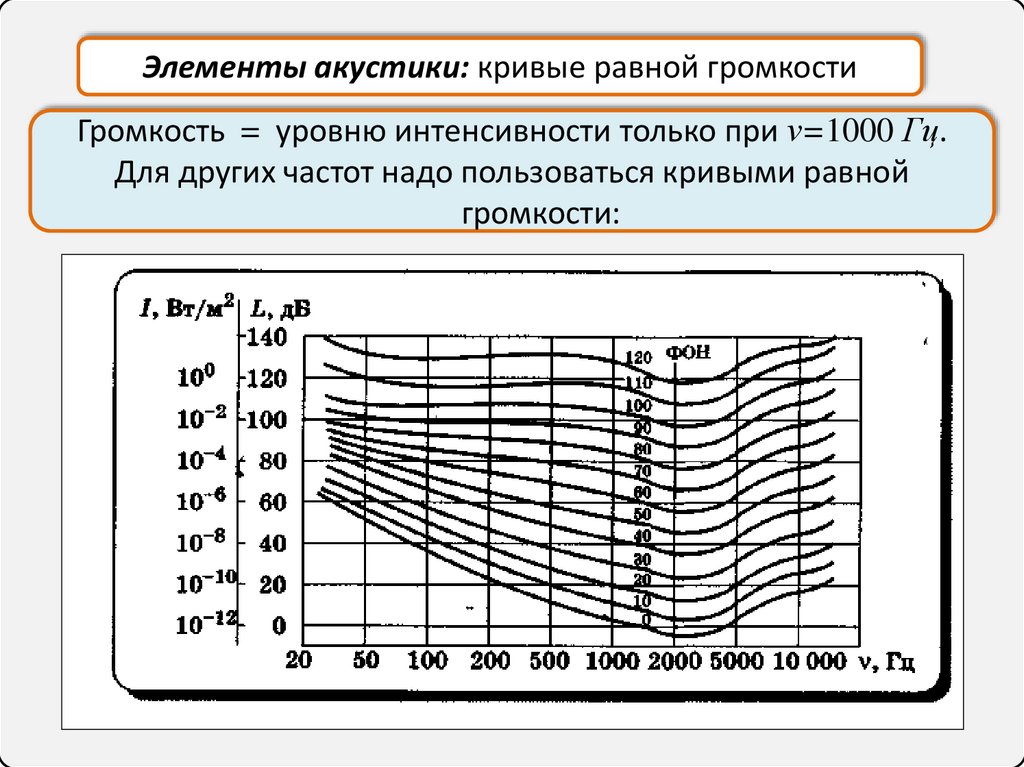
Элементы акустики: кривые равной громкости
Громкость = уровню интенсивности только при ν=1000 Гц.
Для других частот надо пользоваться кривыми равной
громкости:

60.

Элементы акустики: характеристики звуковых волн
Избыточное звуковое давление
p 2 v I v A
Уровень избыточного звукового давления
L p (дБ) 20 lg
Волновое сопротивление Z v
p
p0

61.

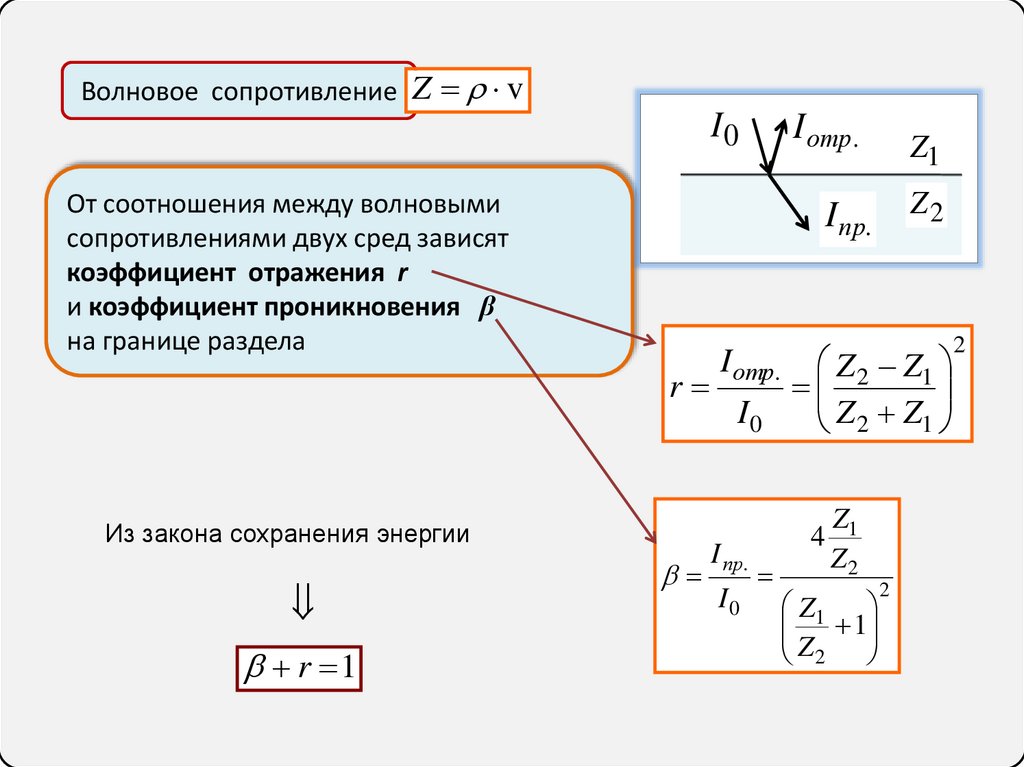
Волновое сопротивление Z v
I0
От соотношения между волновыми
сопротивлениями двух сред зависят
коэффициент отражения r
и коэффициент проникновения β
на границе раздела
Из закона сохранения энергии
r 1
Z1
Z2
I пр.
r
I отр .
I отр.
I0
I пр.
I0
Z 2 Z1
Z 2 Z1
4
Z1
Z2
Z1
1
Z2
2
2

62.

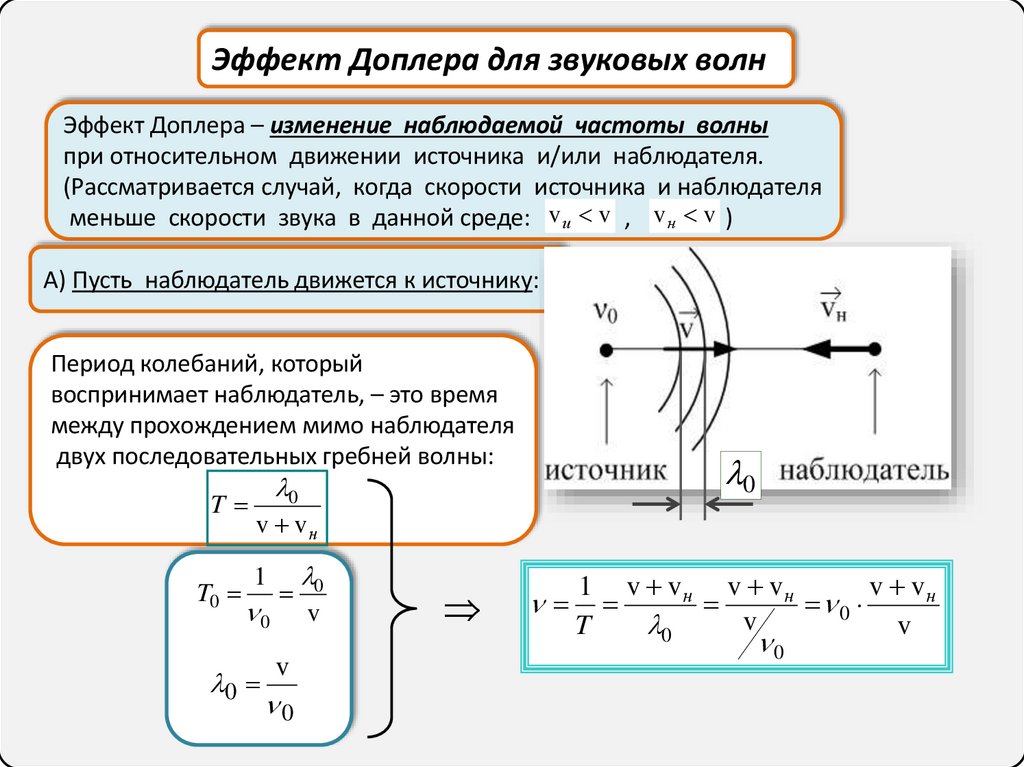
Эффект Доплера для звуковых волн
Эффект Доплера – изменение наблюдаемой частоты волны
при относительном движении источника и/или наблюдателя.
(Рассматривается случай, когда скорости источника и наблюдателя
меньше скорости звука в данной среде: vи v , v н v )
А) Пусть наблюдатель движется к источнику:
Период колебаний, который
воспринимает наблюдатель, – это время
между прохождением мимо наблюдателя
двух последовательных гребней волны:
T
T0
0
0
v vн
1
0
0
v
0
0
v
1 v vн v vн
v vн
0
v
T
0
v
0

63.

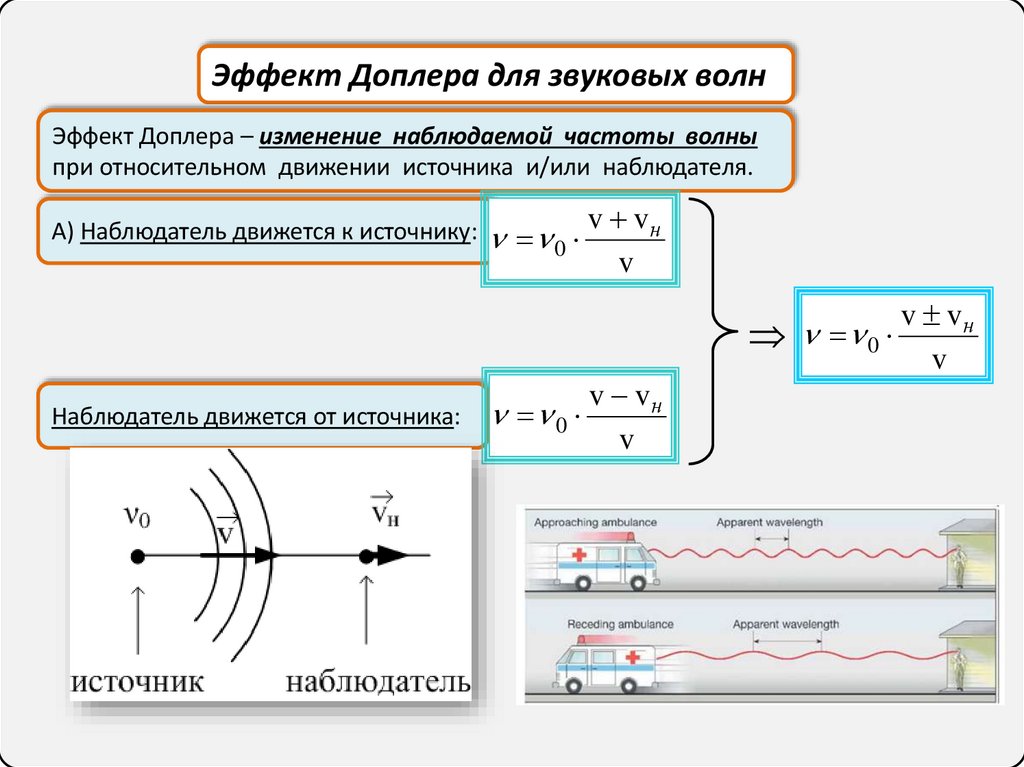
Эффект Доплера для звуковых волн
Эффект Доплера – изменение наблюдаемой частоты волны
при относительном движении источника и/или наблюдателя.
А) Наблюдатель движется к источнику:
0
v vн
v
0
Наблюдатель движется от источника:
0
v vн
v
v vн
v

64.

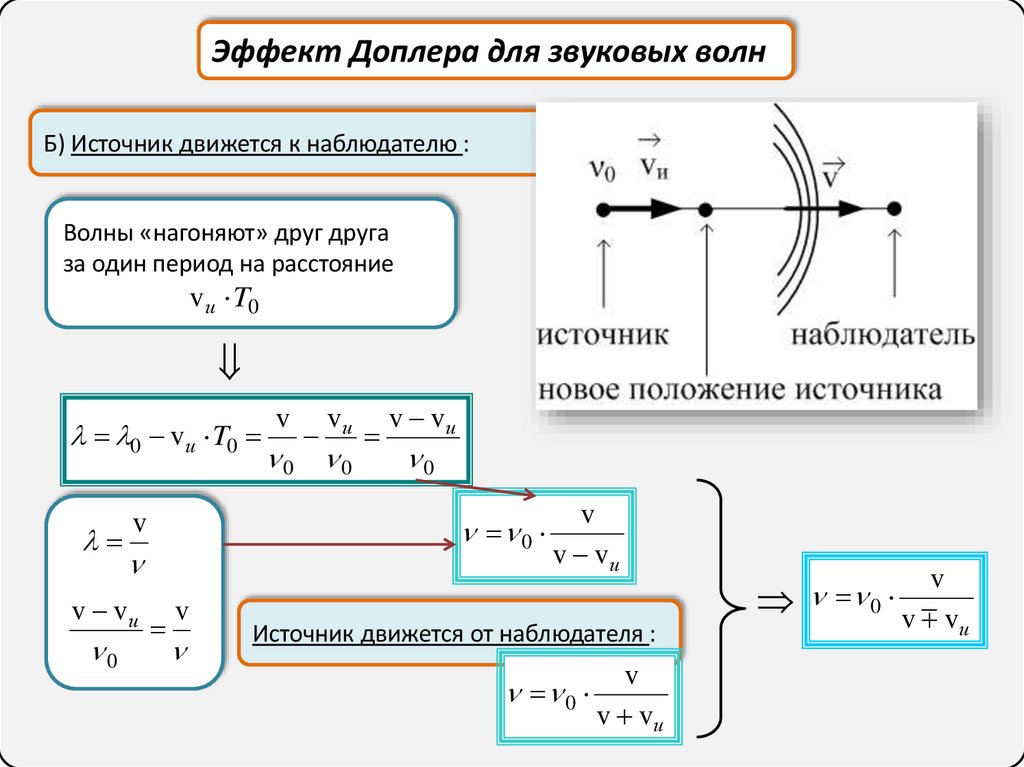
Эффект Доплера для звуковых волн
Б) Источник движется к наблюдателю :
Волны «нагоняют» друг друга
за один период на расстояние
vи T0
0 vи T0
0
vи
0 0
v vи
0
v
0
v vи
v
v vи
v
v
Источник движется от наблюдателя :
0
v
v vи
0
v
v vи

65.

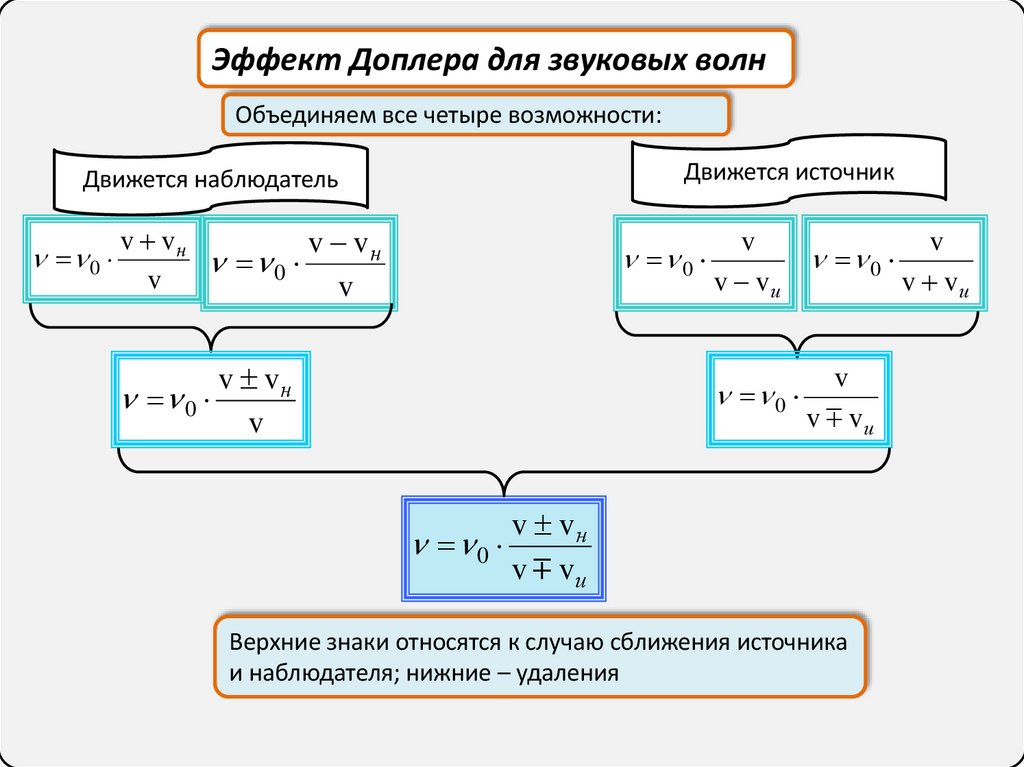
Эффект Доплера для звуковых волн
Объединяем все четыре возможности:
Движется источник
Движется наблюдатель
0
v vн
v vн
0
v
v
0
0
v vн
v
v
v
0
v vи
v vи
0
v
v vи
v vн
0
v vи
Верхние знаки относятся к случаю сближения источника
и наблюдателя; нижние – удаления