Similar presentations:
11_2 Кратные2-24(2)
1.
§ 3. Тройной интегралПусть функция f ( x; y; z ) определена и непрерывна по
совокупности переменных в пространственной области .
Интегральная сумма для функции f ( x; y; z ) по области (телу)
n
имеет вид
Sn f ( xi ; yi ; zi ) Vi ,
i 1
где Vi V ( i ) – объемы элементарных тел i , на которые
разбивается тело ; точки M i ( xi ; yi ; zi ) i – произвольно
выбранные точки в элементарных телах i .
Обозначим: d n max d ( i ) - диаметр разбиения (наибольший из
1 i n
диаметров d ( i ) элементарных областей i , составляющих
разбиение).
2.
Опр. 1. Тройной интеграл от функции f ( x; y; z ) по области(телу) определяется как предел интегральных сумм для
функции f ( x; y; z ) по области при измельчении разбиения:
n
f ( xi ; yi ; zi ) Vi ,
f ( x; y; z )dxdydz dlim
0
n
i 1
если этот предел существует, конечен и не зависит ни от способа
разбиения области на элементарные области, ни от выбора точек
M i в элементарных областях.
2
3.
Свойства тройного интегралаСвойства тройного интеграла повторяют свойства ИФ. В
частности, свойство линейности выражается формулами
kf ( x; y; z )dxdydz k f ( x; y; z )dxdydz
(k const);
f ( x; y; z )dv f ( x; y; z )dv f ( x; y; z )dv
1
2
оценить значение тройного интеграла можно по формуле
mV f ( x; y; z )dxdydz MV ,
где m
min
M ( x ; y ; z )
f ( x; y; z ); M
max
M ( x ; y ; z )
f ( x; y; z ) – наименьшее и
наибольшее значения функции f ( x; y; z ) в области ; V –объем
тела .
3
4.
Если область интегрирования (Ω) разбита на две части (Ω1 ) и(Ω2 ), не имеющие общих внутренних точек, то
f ( x; y; z )dv f ( x; y; z )dv f ( x; y; z )dv
1
2
Теорема о среднем. Если функция f(x,y,z) непрерывна по
совокупности переменным в замкнутой области (Ω), то
найдется такая точка P0(x0,y0,z0)єΩ, что справедливо равенство
f ( x; y; z )dv f ( x0 ; y0 ; z0 ) V , где V – объем области Ω.
Теорема (необходимое условие существования тройного интеграла).
Если функция f(x,y,z) интегрируема в области (Ω), то она ограничена
в этой области.
Теорема(достаточные условия существования тройного интеграла).
Если выполняются условия: 1) область (Ω) – кубируемая (т.е.
имеющая объём), 2) f(x,y,z) ограничена в области (Ω), 3) f(x,y,z)
непрерывна в области (Ω) всюду (за исключением, возможно,
некоторого множества точек объема нуль), то f(x,y,z) интегрируема
в
4
5.
Основные геометрические и физические приложениятройного интеграла
1. Объем пространственного тела равен тройному интегралу по
области от единицы: V dxdydz.
2. Масса тела равна тройному интегралу по области от
плотности ( x; y; z ) этого тела: m ( x; y; z )dxdydz.
3. Координаты центра тяжести тела , плотность которого в
каждой точке M ( x; y; z ) задается функцией ( x; y; z) 0 :
x ( x; y; z )dxdydz
y ( x; y; z )dxdydz
xC
; yC
( x; y; z )dxdydz
( x; y; z )dxdydz
;
z ( x; y; z )dxdydz
zC
( x; y; z )dxdydz
.
5
6.
Статические моменты тела G относительно координатныхплоскостей
S xy z ( x, y, z )dxdydz , S xz y ( x, y, z )dxdydz ,
G
G
S yz x ( x, y, z )dxdydz
G
Моменты инерции тела G относительно координатных
плоскостей равны
I xy z 2 ( x, y, z )dxdydz , I xz y 2 ( x, y, z )dxdydz ,
G
G
I yz x 2 ( x, y, z )dxdydz
G
6
7.
Моменты инерции относительно координатных осей Ох, Оу,Oz и полярный момент инерции I0 относительно начала
координат равны:
G
G
I z x 2 y 2 ( x, y, z )dxdydz , I 0 x 2 y 2 z 2 ( x, y, z )dxdydz
G
G
I x y 2 z 2 ( x, y, z )dxdydz , I y x 2 z 2 ( x, y, z )dxdydz ,
Для однородного тела γ(x,y,z)=const и в некоторых задачах
полагают γ=1.
7
8.
Вычисление тройных интегралов.Вычисление тройного интеграла f x, y, z dv так же как и
двойного, может быть осуществлено посредством ряда
последовательных интегрирований, т.е. сводится к вычислению
интеградлов меньшей кратности.
Декартовы координаты.
Пусть дан тройной интеграл от функции f(x,y,z) I f x, y, z dv
причем область Ω отнесена к системе декартовых координат Oxyz.
Разобьем область Ω плоскостями, параллельными координатным
плоскостям.
Тогда
частичными
областями
будут
параллелепипеды с гранями, параллельными плоскостям Oxy,
Oxz, Oyz.
Элемент объема будет равен произведению дифференциалов
переменных интегрирования dv=dxdydz.
В соответствии с этим
I f x, y, z dx dy dz
8
9.
Рассмотрим область V, ограниченнуюснизу и сверху поверхностями z=z1(x;y)
и z=z2 (x;y), и боковой цилиндрической
поверхностью
с
образующими,
параллельными оси Oz. Пусть область
D — проекция тела на плоскость Oxy ,
в которой определены и непрерывны
функции z=z1(x;y) и z=z2 (x;y).
Можно показать, что для любой
непрерывной в области V
функции f (x;y;z) имеет место
формула
z2 x , y
f x, y, z dx dy dz dxdy f x, y, z dz
V
D
z1 x ; y
При этом сначала вычисляется внутренний интеграл по
переменной z (при постоянных x и y), а затем внешний двойной
9
интеграл по области D.
10.
Внутренний интегралF x; y
z2 x ; y
f x; y; z dz
z1 x ; y
представляет собой функцию двух переменных х и у. При
интегрировании x и y рассматриваются здесь как постоянные.
Получим значение искомого тройного интеграла, если
возьмем интеграл от функции F(x;y) при условии, что точка
P(x;y) изменяется по области D, т.е.
F x; y dxdy
D
Приводя, далее, двойной интеграл по области D к повторному
и интегрируя сначала по y, а затем по x, получим
z2 x , y
b
y2 x
z2 x , y
z1 x ; y
a
y1 x
z1 x ; y
f x, y, z dx dy dz dxdy f x, y, z dz dx dy f x, y, z dz
V
D
где y1(x) и y2(x) — ординаты точек «входа» в область D и
«выхода» из нее прямой x=const (в плоскости Oxy), а a и b—
абсциссы конечных точек интервала оси Ox, на которой
10
проектируется область D.
11.
Вывод.Вычисление
тройного
интеграла
сводится
к
последовательному вычислению трех определенных интегралов
(если область интегрирования имеет несложную форму).
Пусть тело ограничено снизу поверхностью z z1 ( x; y ), сверху
поверхностью z z2 ( x; y ) и проектируется на плоскость Оxу в
область D. Тогда тело называется правильным в направлении
оси Оz, так как любая прямая, параллельная оси Оz, пересекает
границу тела не более двух раз. Если область D, на которую
проектируется тело , является правильной в направлении оси
Оу, то
{( x; y; z ) : z1 ( x; y ) z z2 ( x; y ), y1 ( x ) y y2 ( x ), a x b}.
Тогда формула сведения тройного интеграла к повторному:
b
y2 ( x )
z2 ( x ; y )
f ( x; y; z )dxdydz dx dy
a
y1 ( x )
z1 ( x ; y )
f ( x; y; z )dz.
12.
Выражение, стоящее в правой части формулы, называетсяповторным (трехкратным) интегралом.
Замечание. При сведении тройного интеграла к повторному тело
можно проектировать не на плоскость Оxy, а на ту
координатную плоскость, на которую удобнее. При этом порядок
интегрирования в повторном интеграле будет другим.
Для вычисления тройного интеграла от данной функции по
данной области рекомендуется действовать по следующей
схеме.
1) Строится в системе координат Oxyz область интегрирования.
2) Выбираем порядок интегрирования, который, в основном,
диктуется видом самой области интегрирования. Область
проецируется на одну из трех координатных плоскостей. В
результате мы определяем проекцию области Ω - плоскую
область D и уравнения поверхностей, которые ограничивают
область Ω
12
13.
3) Выносим, для удобства, проекцию – область D на отдельныйрисунок и дальнейшую расстановку пределов осуществляем как
в двойном интеграле.
4) В результате такой подготовительной работы мы определяем
пределы изменения для каждой из трех переменных x,y,z.
Если последовательность интегрирования выбрана в таком порядке:
внутреннее по z, z1(x;y) z z2 (x;y), y1(x) y y2 (x), a x b
13
14.
Примеры расстановки пределов интегрирования в тройноминтеграле по различным областям
x = 0, x = a,
y = 0, y = b,
z = 0, z = c
а
b
c
f
(
x
;
y
;
z
)
dx
dy
dz
dx
dy
f
(
x
,
y
,
z
)
dz
(V )
0
0
0
14
15.
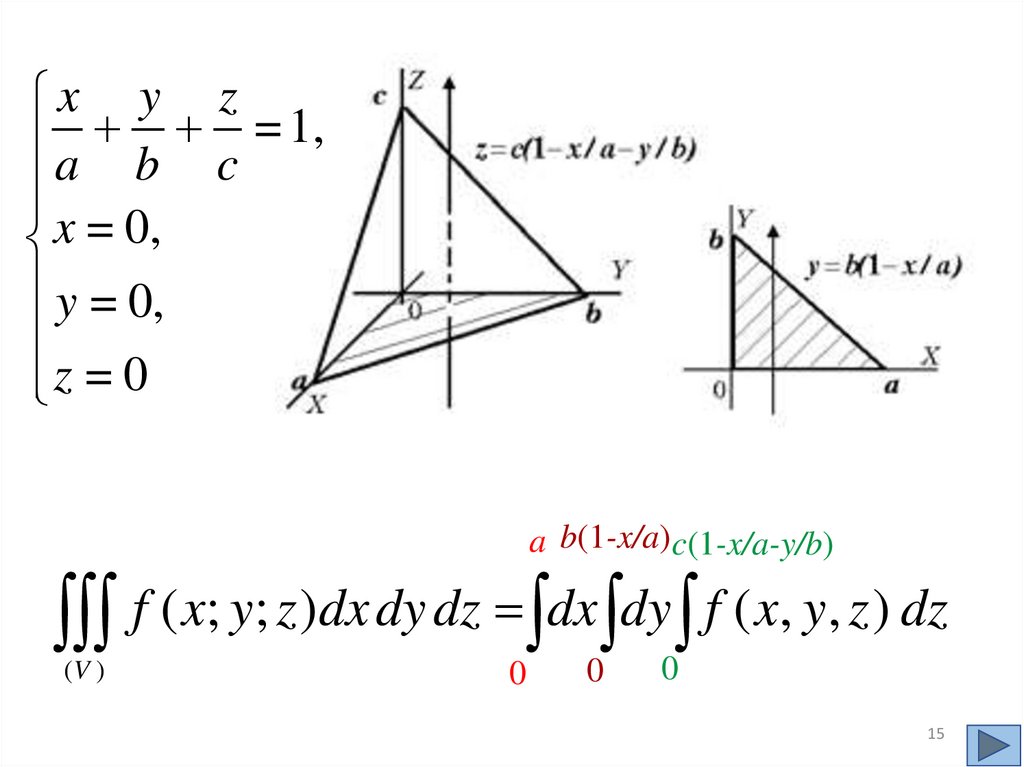
x y za b c = 1,
x = 0,
y = 0,
z = 0
a b(1-x/a) c(1-x/a-y/b)
f
(
x
;
y
;
z
)
dx
dy
dz
dx
dy
f
(
x
,
y
,
z
)
dz
(V )
0
0
0
15
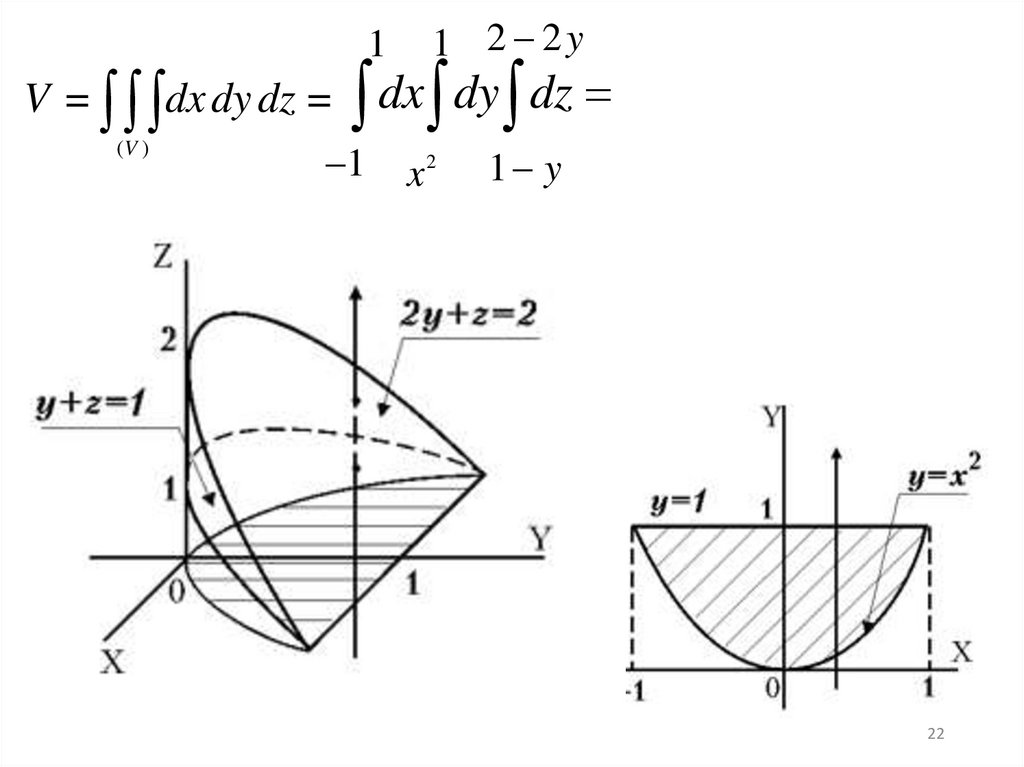
16.
z = 1 x ,y = 0, y = 2,
z 0
2
2
1
1-x2
f ( x; y; z )dx dy dz dx dy f ( x, y, z ) dz
(V )
-1
0
0
17.
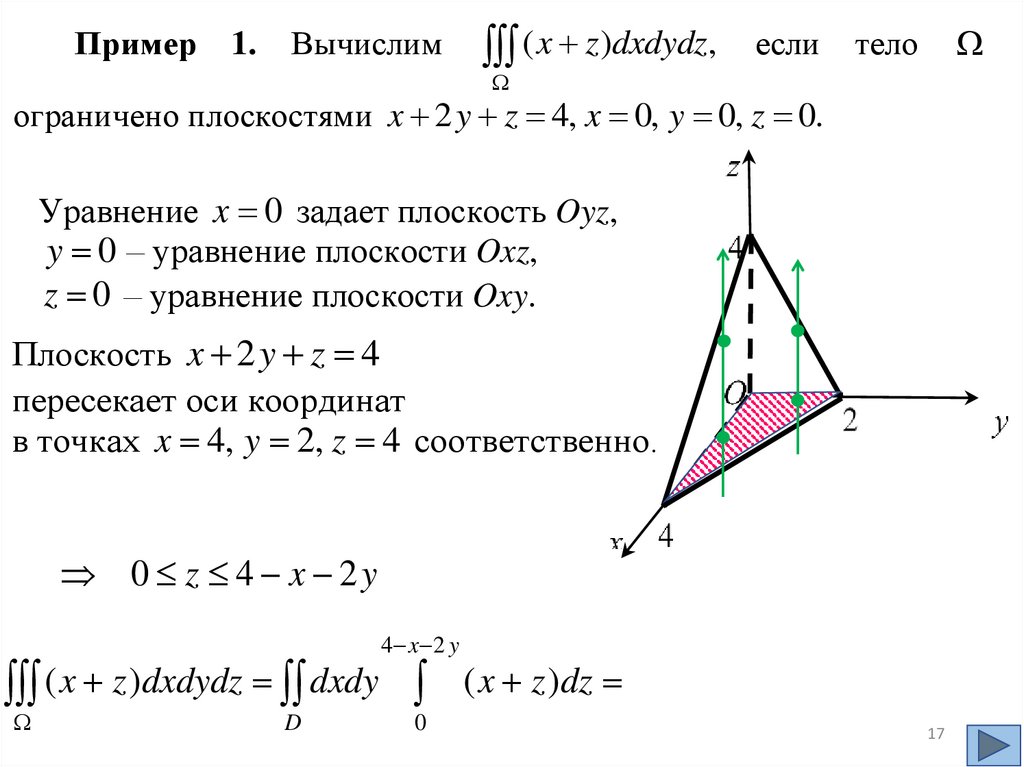
Пример1.
Вычислим
( x z)dxdydz,
если
тело
ограничено плоскостями x 2 y z 4, x 0, y 0, z 0.
Уравнение x 0 задает плоскость Oyz,
y 0 – уравнение плоскости Oxz,
z 0 – уравнение плоскости Oxy.
Плоскость x 2 y z 4
пересекает оси координат
в точках x 4, y 2, z 4 соответственно.
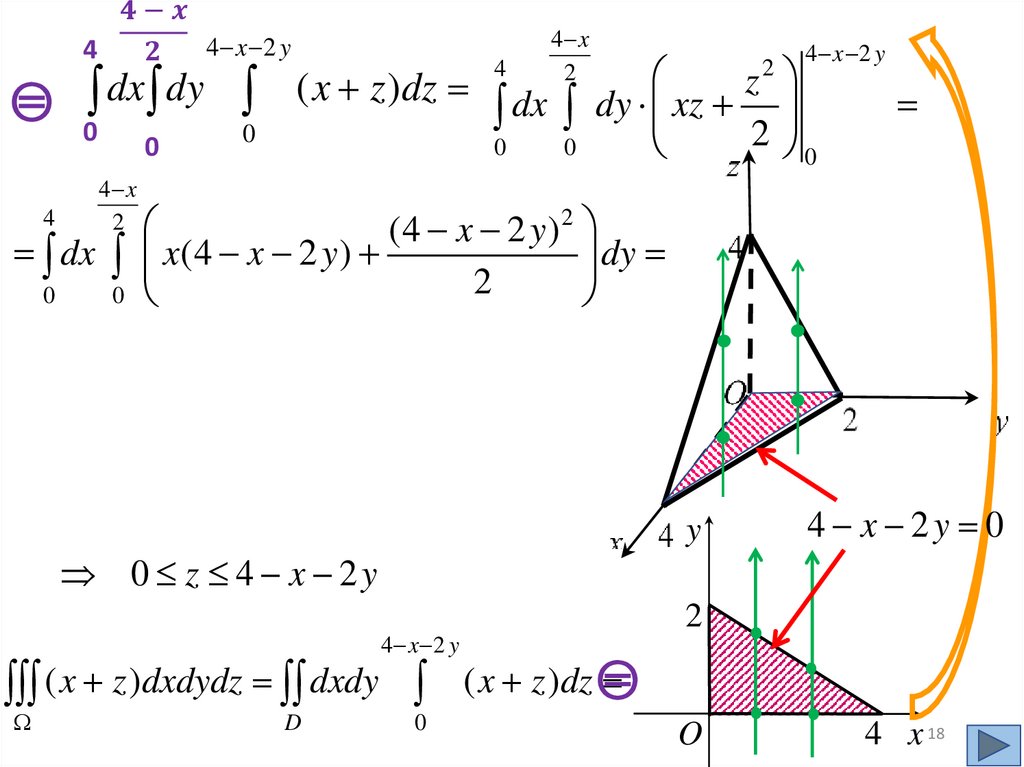
0 z 4 x 2y
4 x 2 y
( x z )dxdydz dxdy
D
0
( x z )dz
17














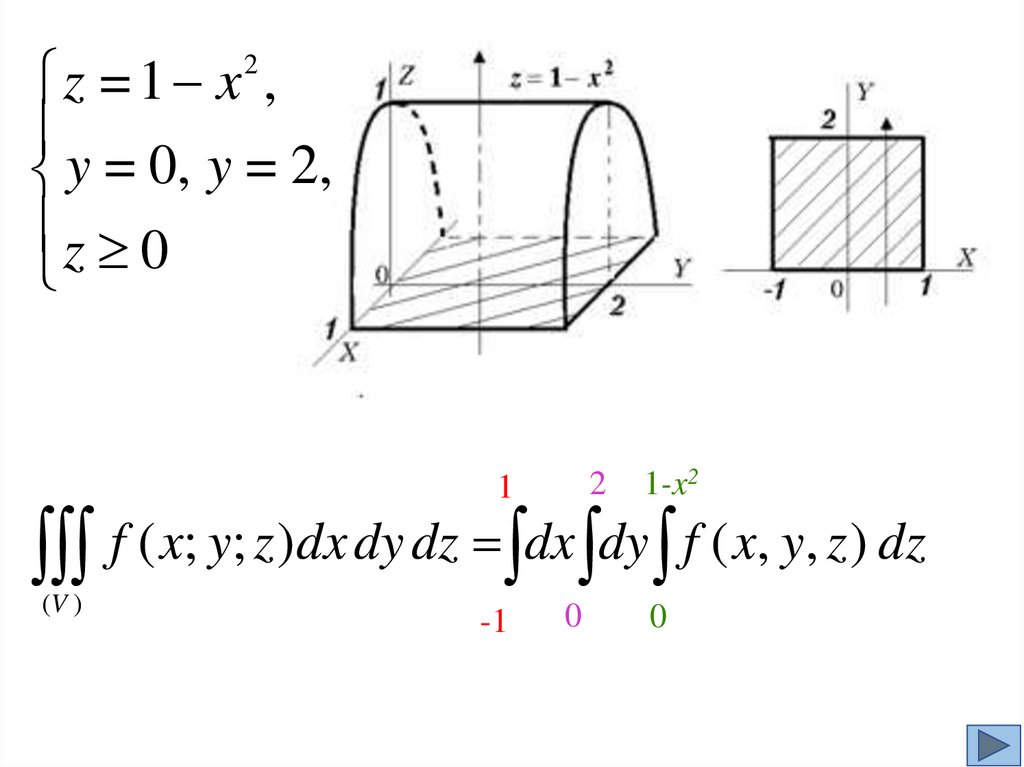
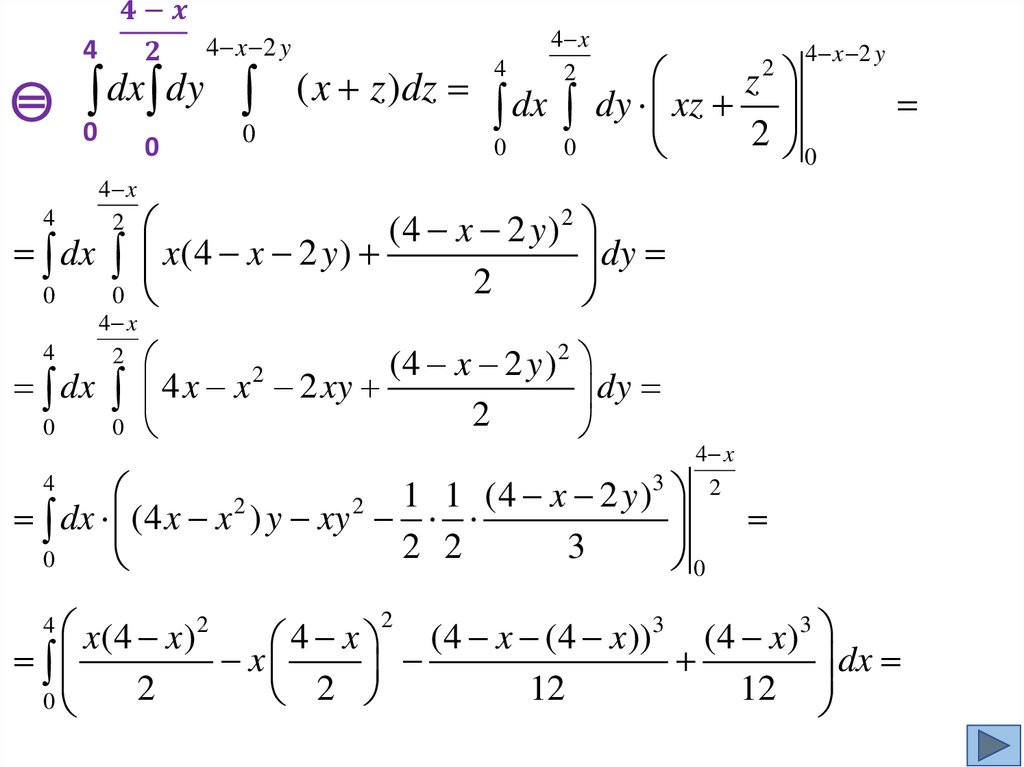
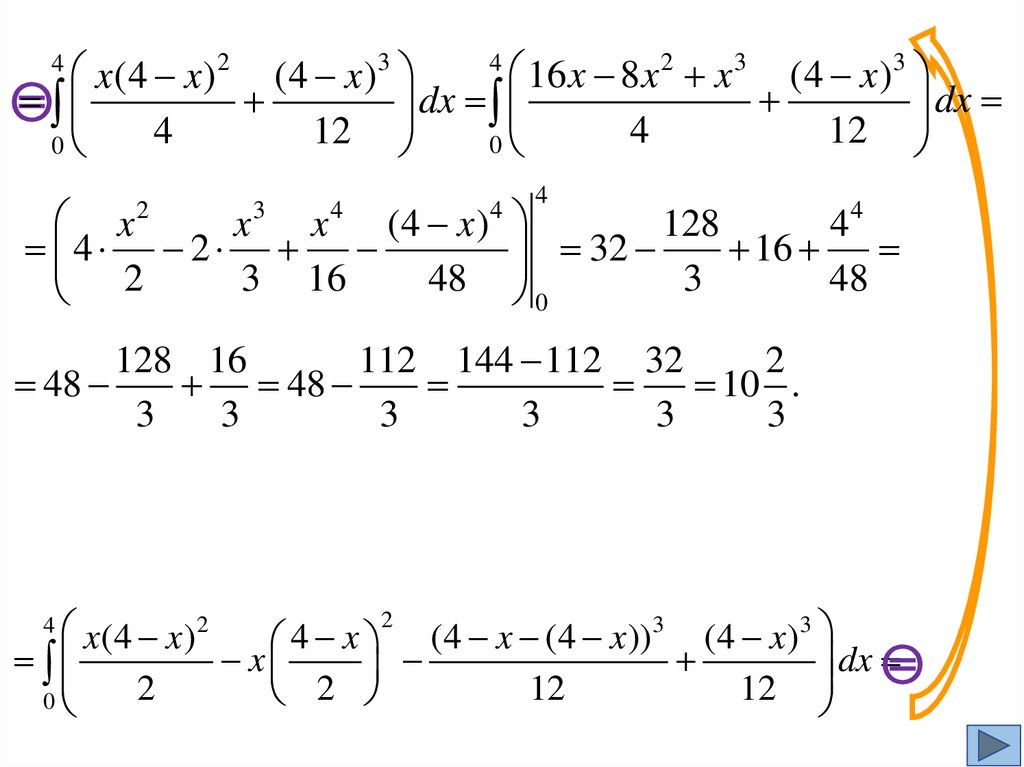

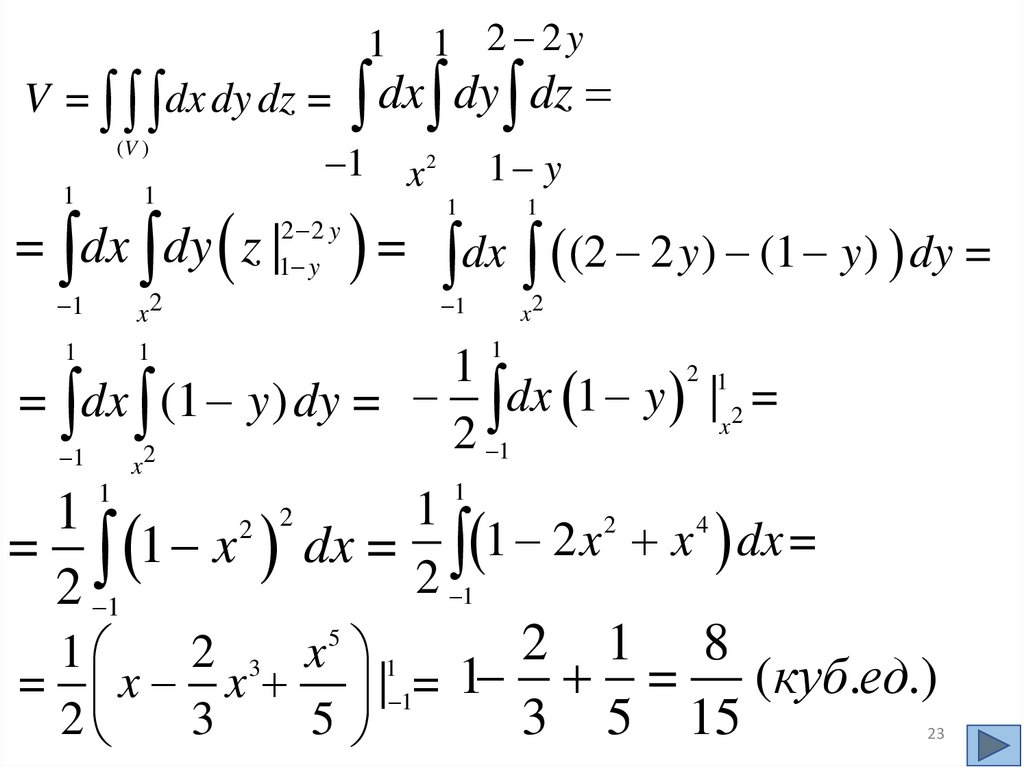



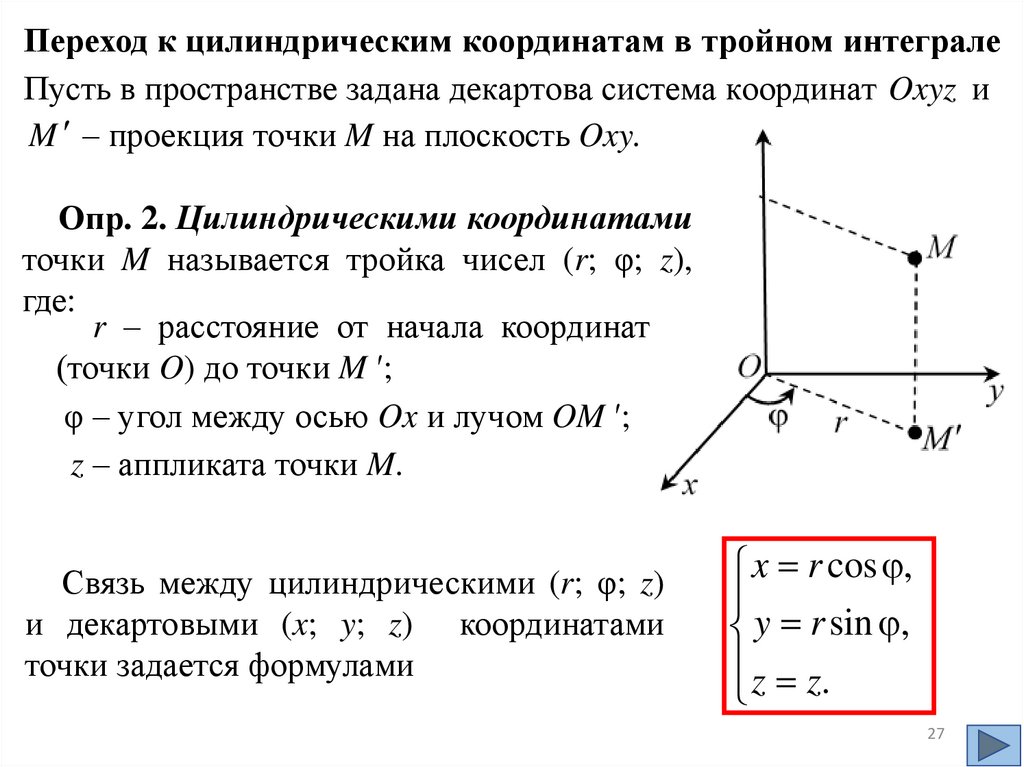
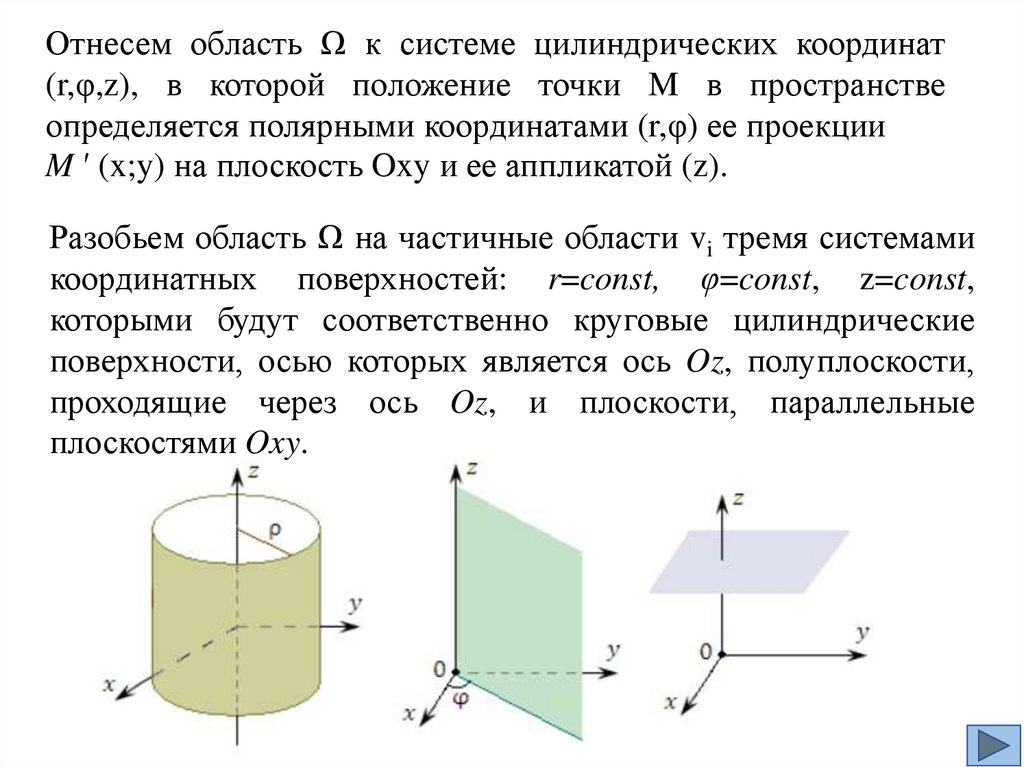







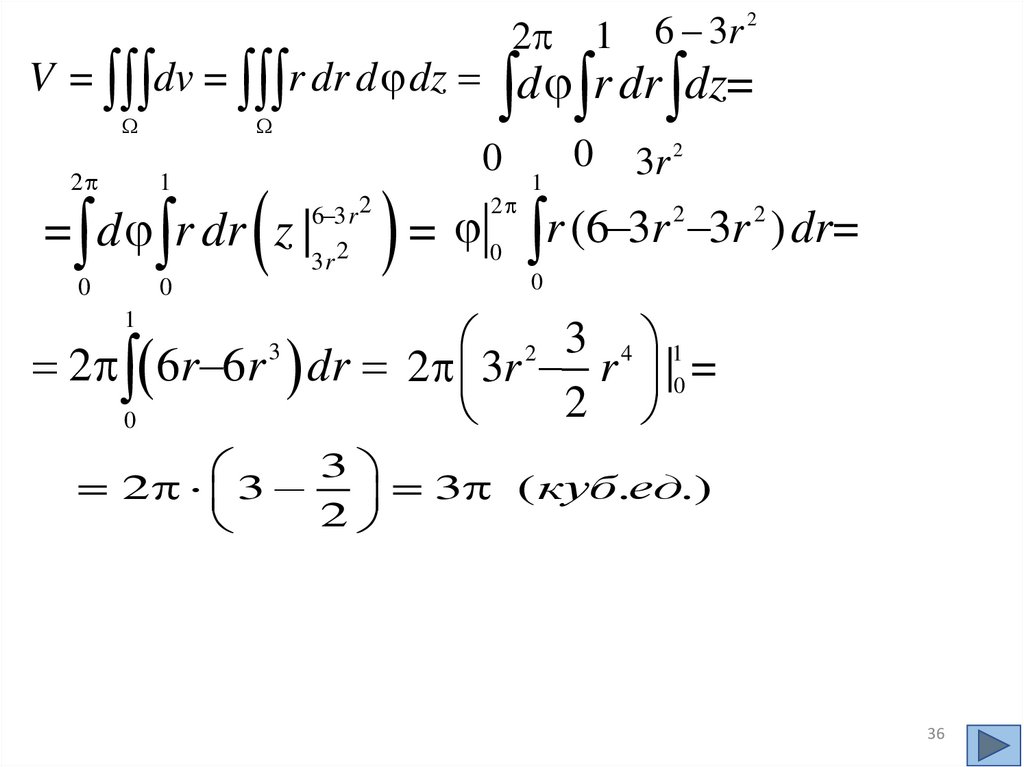





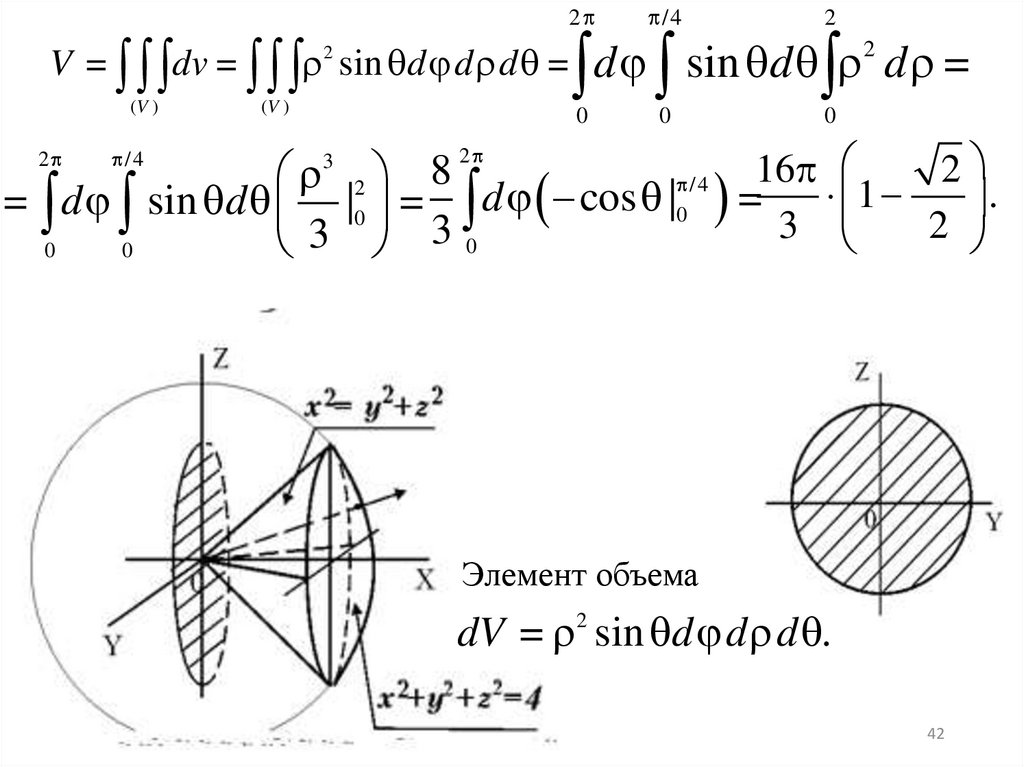

 mathematics
mathematics








