практика 12 операт. метод

1.

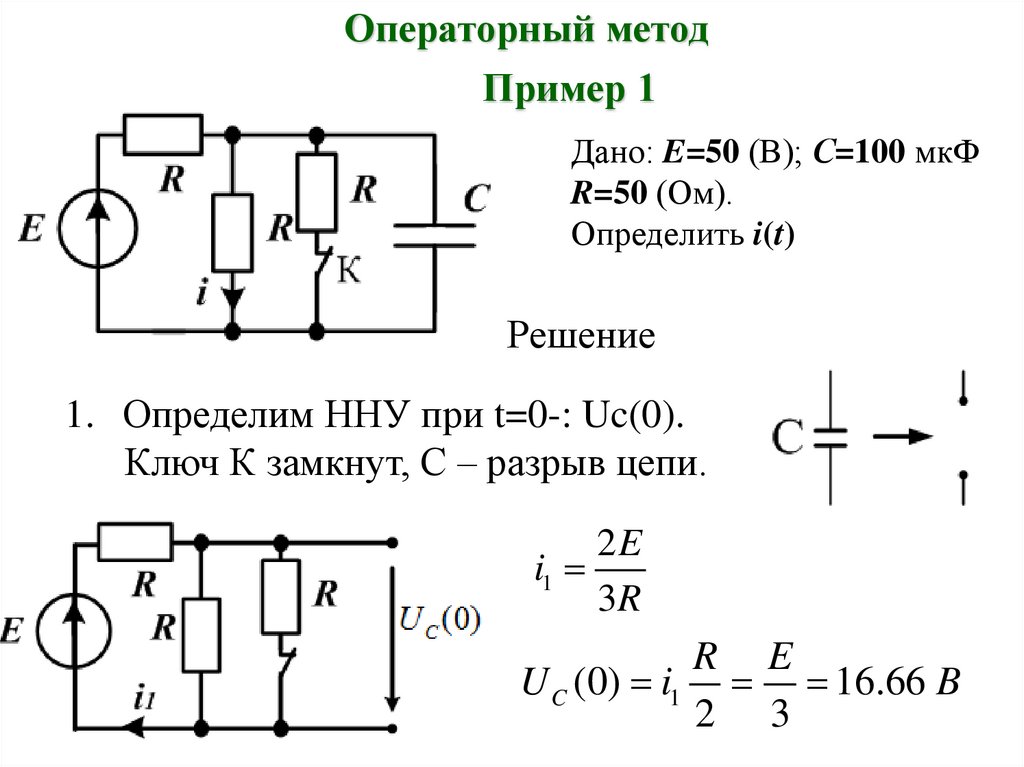
Операторный метод
Пример 1
Дано: E=50 (В); С=100 мкФ
R=50 (Ом).
Определить i(t)
Решение
1. Определим ННУ при t=0-: Uc(0).
Ключ К замкнут, С – разрыв цепи.
2E
i1
3R
R E
U C (0) i1 16.66 B
2 3

2.

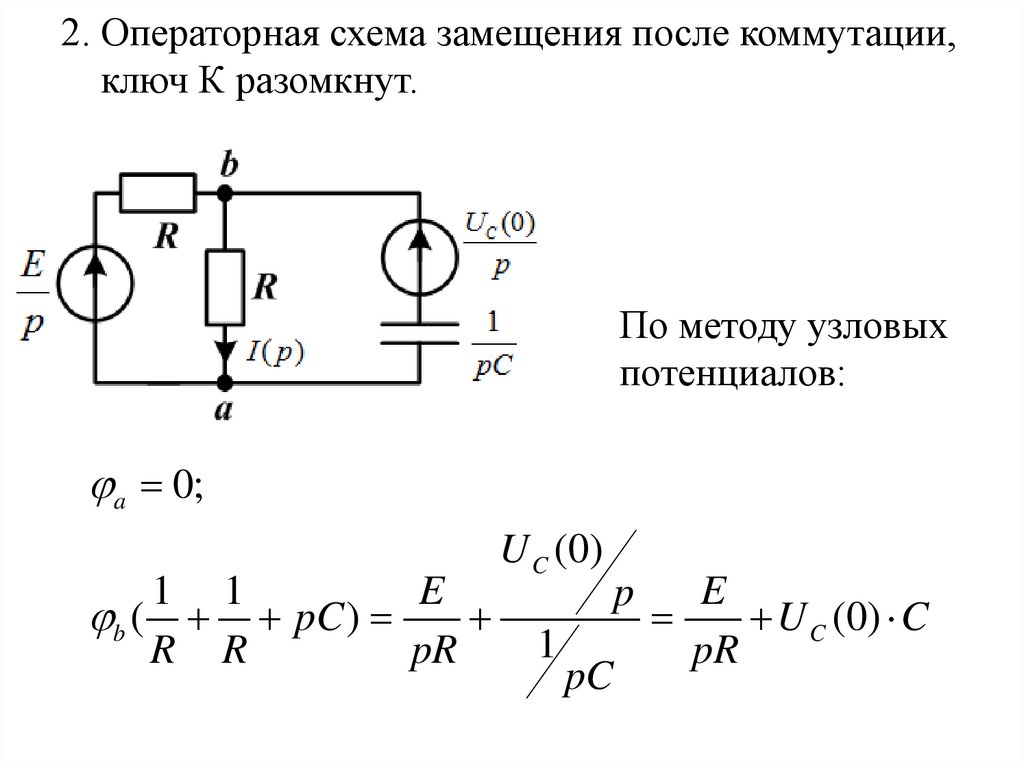
2. Операторная схема замещения после коммутации,
ключ К разомкнут.
По методу узловых
потенциалов:
a 0;
1 1
E
b ( pC )
R R
pR
U C (0)
1
pC
p
E
U C (0) C
pR

3.

Получаем:
E U C (0) RCp
b E U C (0) RCp
b
; I ( p)
p (2 RCp )
R
p (2 R R 2Cp )
50 16.66 5 10 3 p
50 0.833 p
A( p)
I ( p)
p (100 0.25 p )
p (100 0.25 p ) p B1 ( p )
По теореме разложения:
100
B1 ( p ) 100 0.25 p 0, получаем p1
400 1 c
0.25
B ( p ) (100 0.25 p) 0.25
'
1
'
A( p1 )
A(0)
50 50 0.0833 ( 400) 400t
p1t
i (t )
e
e
'
B1 (0) p1 B1 ( p1 )
100
( 400) 0.25
0.5 0.1668 e 400t A

4.

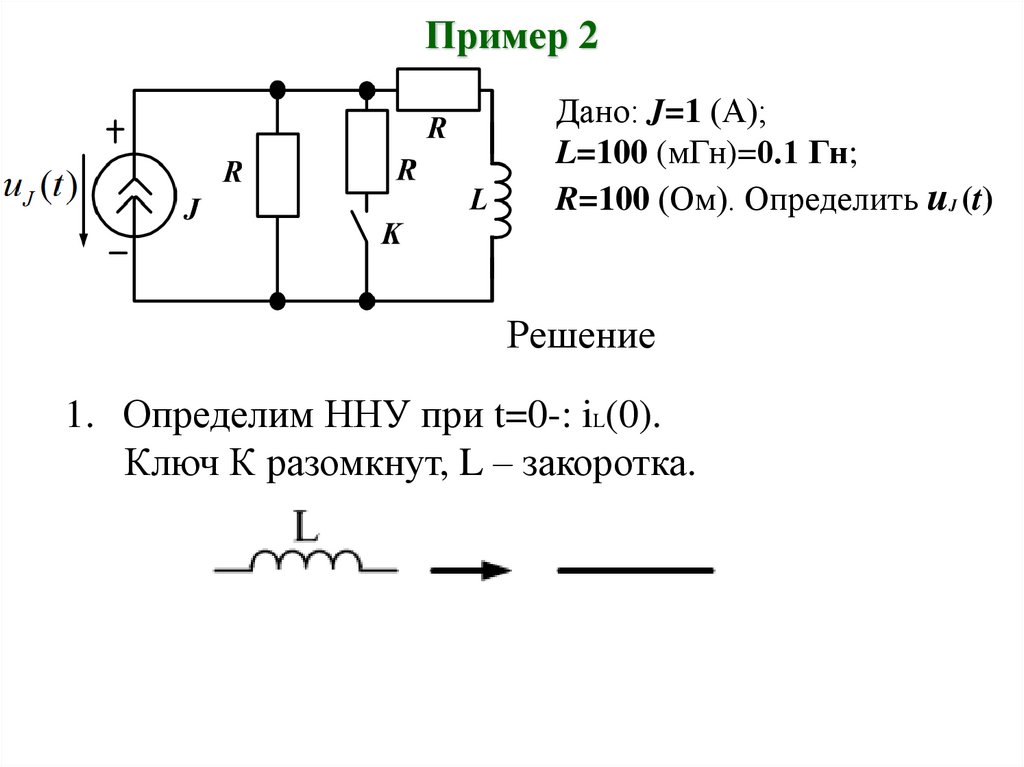
Пример 2
Дано: J=1 (А);
L=100 (мГн)=0.1 Гн;
R=100 (Ом). Определить uJ (t)
Решение
1. Определим ННУ при t=0-: iL(0).
Ключ К разомкнут, L – закоротка.

5.

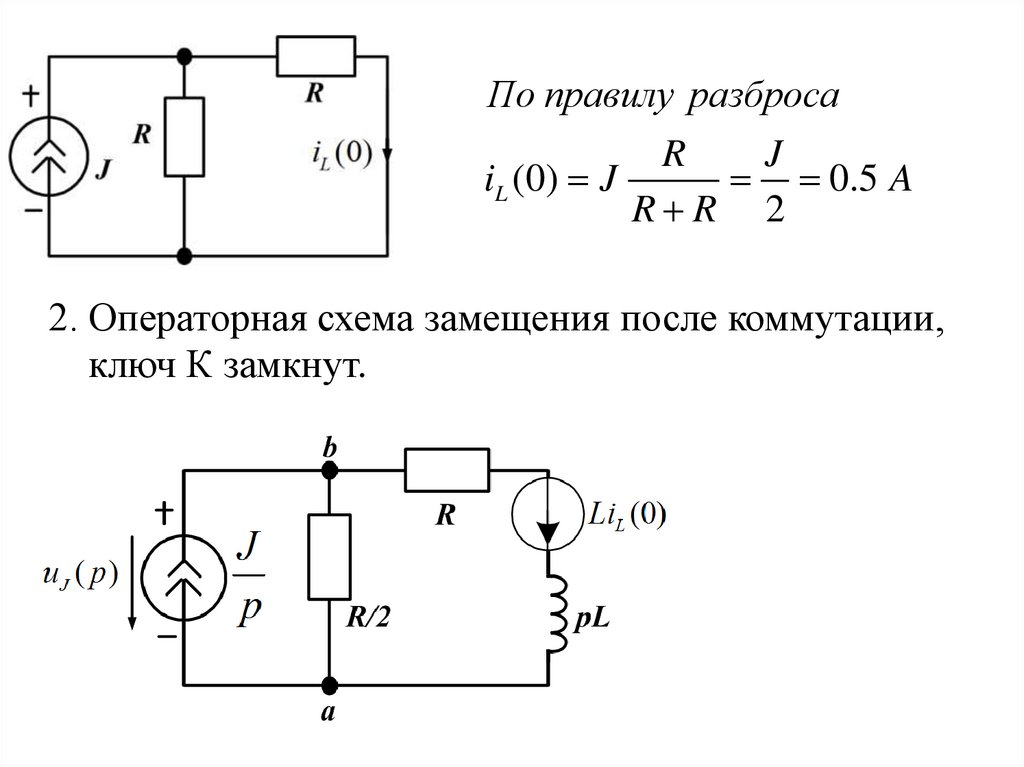
По правилу разброса
R
J
iL (0) J
0.5 A
R R 2
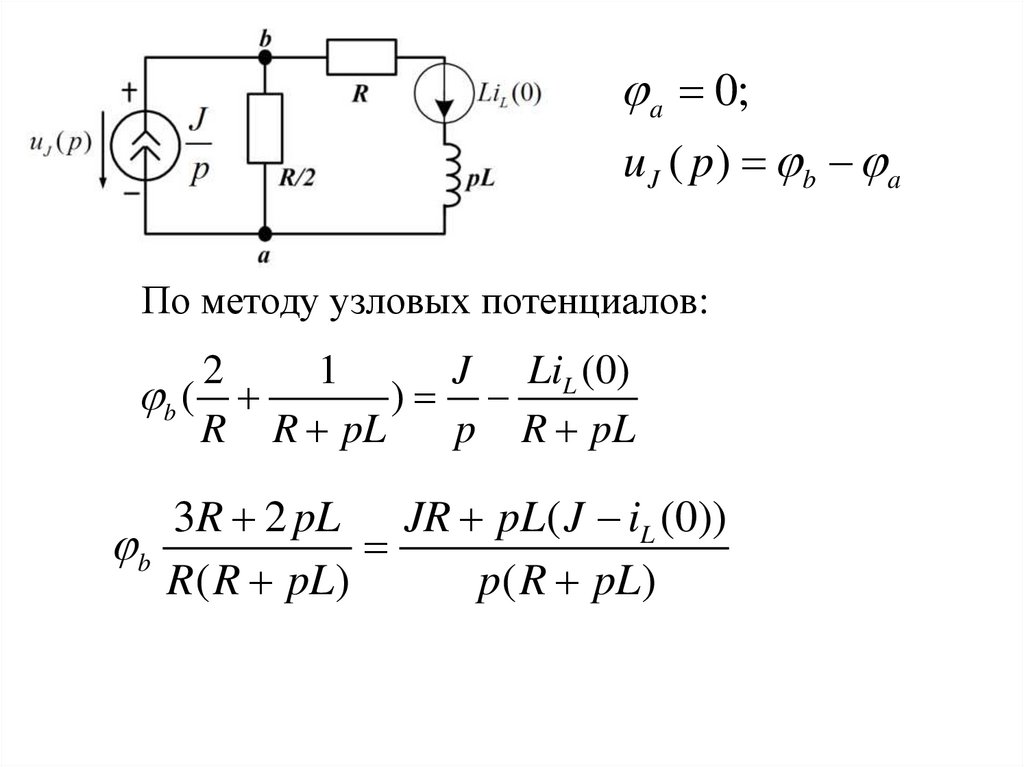
2. Операторная схема замещения после коммутации,
ключ К замкнут.

6.

a 0;
u J ( p ) b a
По методу узловых потенциалов:
2
1
J LiL (0)
b (
)
R R pL
p R pL
3R 2 pL JR pL( J iL (0))
b
R( R pL)
p ( R pL)

7.

JR 2 RpL( J iL (0))
104 5 p
A( p)
u J ( p ) b
p (3R 2 pL)
p (300 0.2 p) p B1 ( p )
По теореме разложения:
B1 ( p ) 300 0.2 p 0, получаем p1 1500 1 c
B1 (0) 300
B1' ( p ) (300 0.2 p) ' 0.2
4
4
A( p1 )
A(0)
10
10
5 1500 1500t
p1t
u J (t )
e
e
'
B1 (0) p1 B1 ( p1 )
300 1500 0.2
33.3 8.33e 1500t B

8.

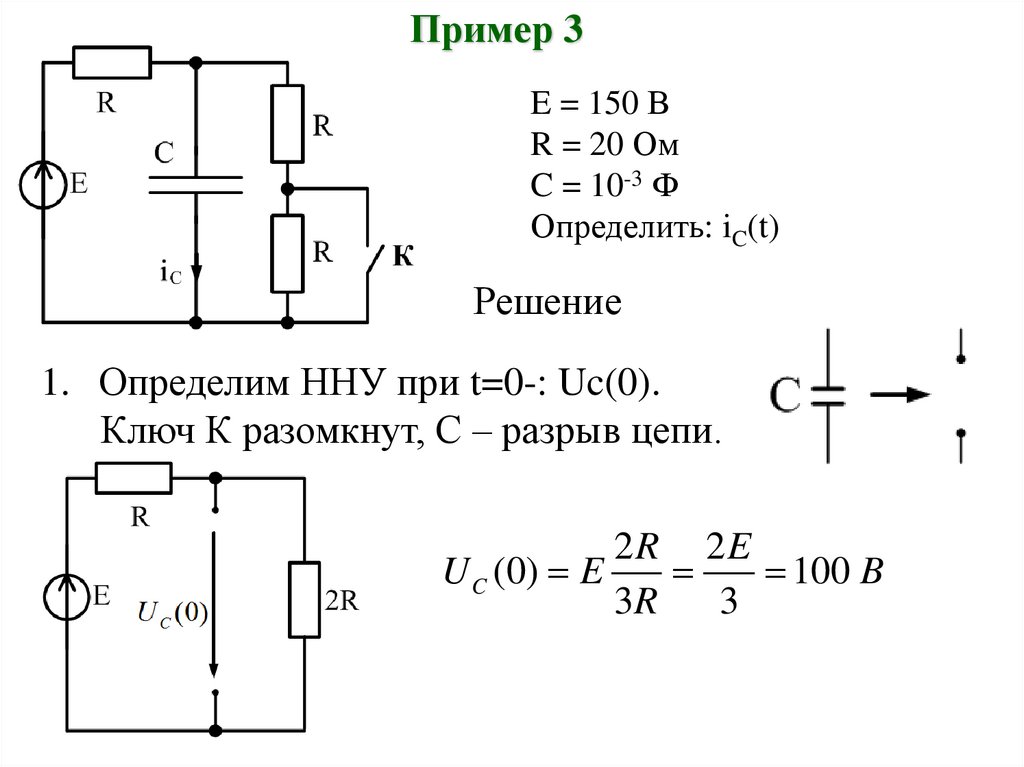
Пример 3
E = 150 В
R = 20 Ом
C = 10-3 Ф
Определить: iC(t)
Решение
1. Определим ННУ при t=0-: Uc(0).
Ключ К разомкнут, С – разрыв цепи.
2R 2E
U C (0) E
100 B
3R
3

9.

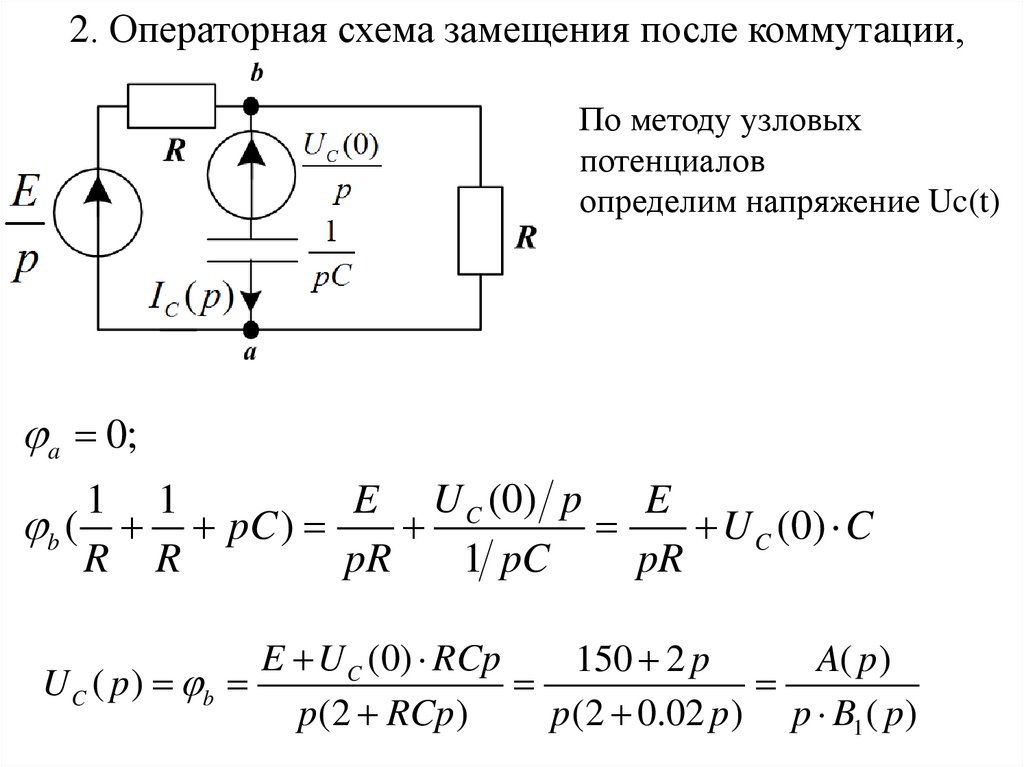
2. Операторная схема замещения после коммутации,
ключ К замкнут.
По методу узловых
потенциалов
определим напряжение Uc(t)
a 0;
1 1
E U C (0) p E
b ( pC )
U C (0) C
R R
pR
1 pC
pR
E U C (0) RCp
150 2 p
A( p)
U C ( p ) b
p (2 RCp )
p(2 0.02 p) p B1 ( p)

10.

По теореме разложения:
B1 ( p) 2 0.02 p 0, получаем p1 100 1 c
B1' ( p ) (2 0.02 p) ' 0.02
A( p1 )
A(0)
150 150 2 ( 100) 100t
p1t
uC (t )
e
e
'
B1 (0) p1 B1 ( p1 )
2
( 100) 0.02
75 25 e 100t B
Определим ток в емкости:
duC (t )
iC (t ) C
10 3 25 ( 100)e 100t 2.5e 100t A
dt

11.

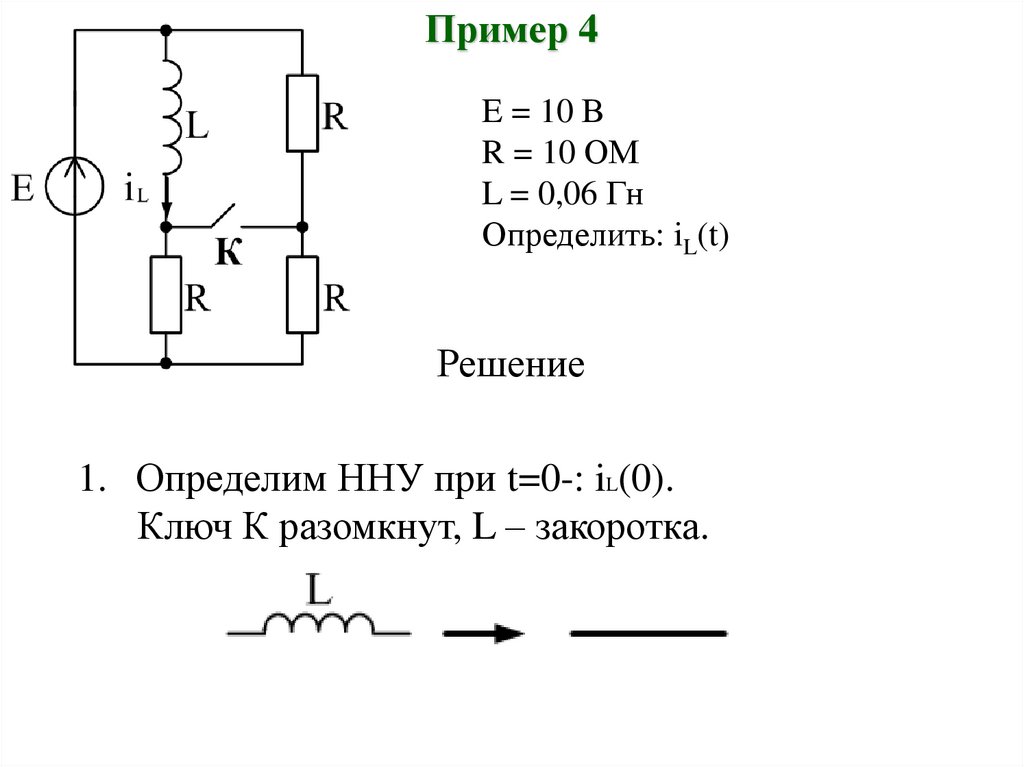
Пример 4
E = 10 В
R = 10 ОМ
L = 0,06 Гн
Определить: iL(t)
Решение
1. Определим ННУ при t=0-: iL(0).
Ключ К разомкнут, L – закоротка.

12.

E
iL (0) 1 A
R
2. Операторная схема замещения после
коммутации, ключ К замкнут.

13.

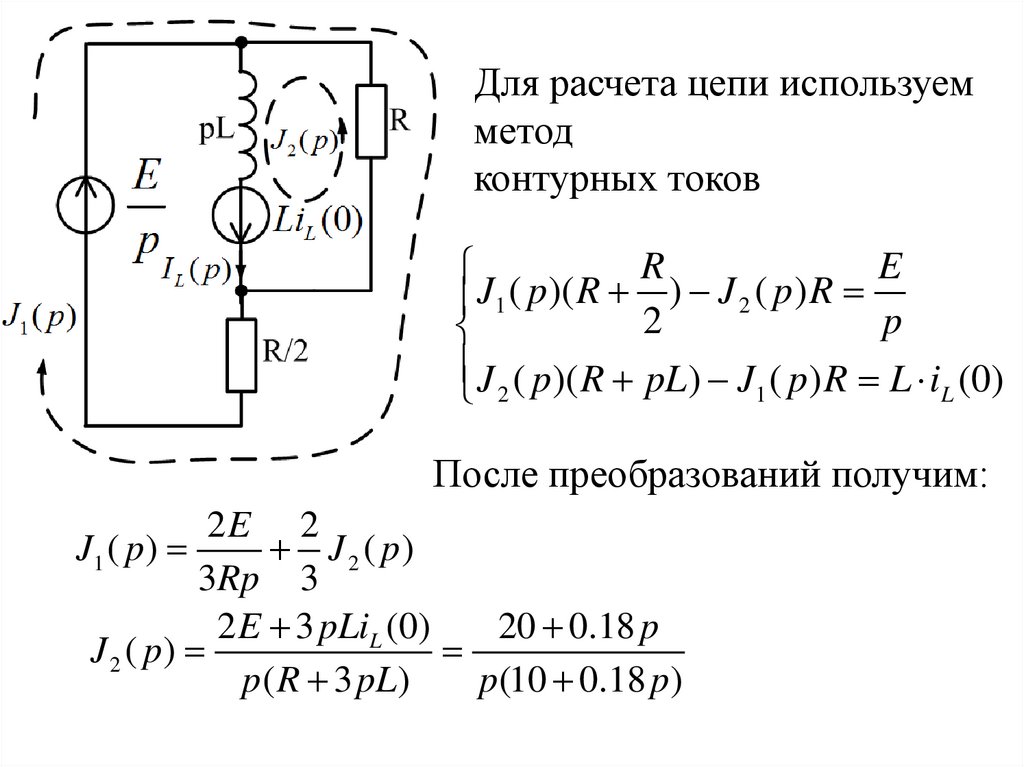
Для расчета цепи используем
метод
контурных токов
R
E
J1 ( p)( R ) J 2 ( p) R
2
p
J ( p )( R pL) J ( p ) R L i (0)
2
1
L
После преобразований получим:
2E 2
J1 ( p )
J 2 ( p)
3Rp 3
2 E 3 pLiL (0)
20 0.18 p
J 2 ( p)
p ( R 3 pL)
p (10 0.18 p)

14.

По теореме разложения:
B1 ( p) 10 0.18 p 0, получаем p1 55.55 1 c
B1' ( p ) (10 0.18 p)' 0.18
A( p1 )
A(0)
p1t
iL (t ) J 2 ( p )
e
'
B1 (0) p1 B1 ( p1 )
20 20 0.18 ( 55.55) 55.55t
e
10
( 55.55) 0.18
2 1 e 55.55t A

15.

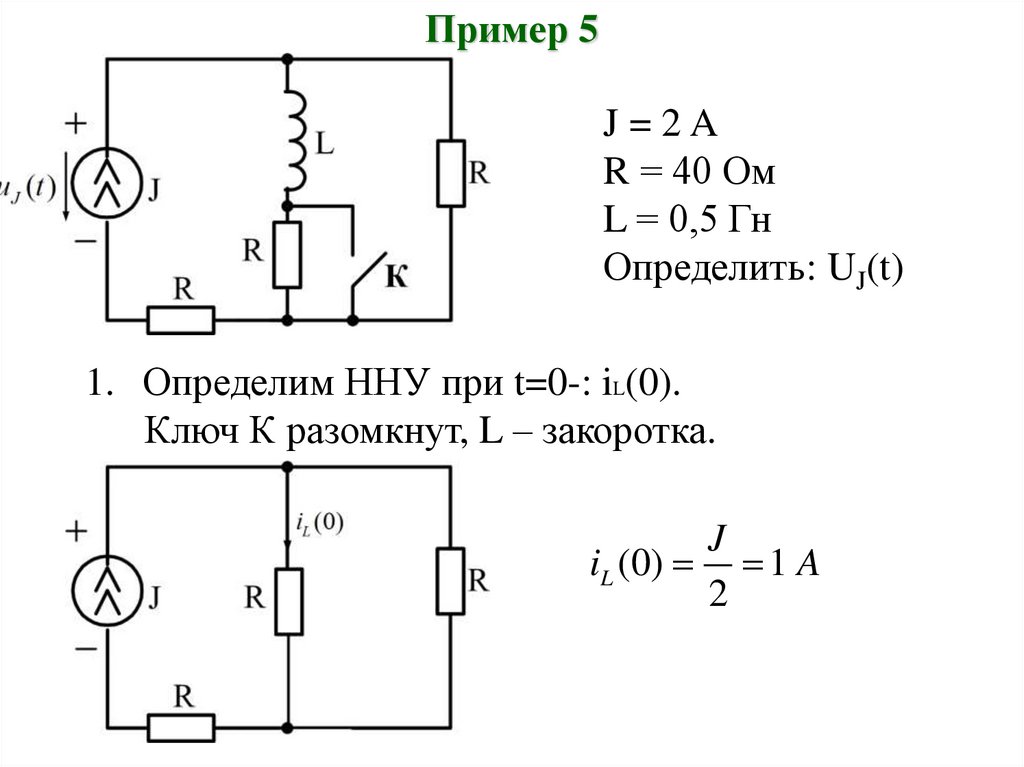
Пример 5
J=2A
R = 40 Ом
L = 0,5 Гн
Определить: UJ(t)
1. Определим ННУ при t=0-: iL(0).
Ключ К разомкнут, L – закоротка.
J
iL (0) 1 A
2

16.

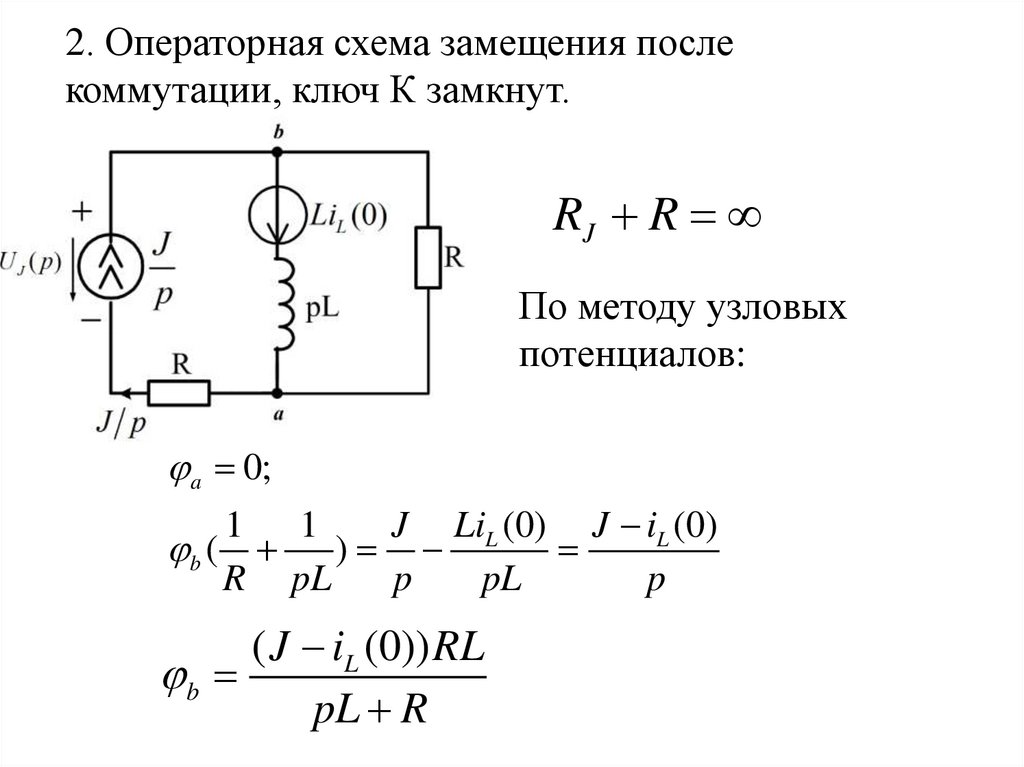
2. Операторная схема замещения после
коммутации, ключ К замкнут.
RJ R
По методу узловых
потенциалов:
a 0;
1 1
J LiL (0) J iL (0)
b ( )
R pL
p
pL
p
( J iL (0)) RL
b
pL R

17.

По 2 закону Кирхгофа:
( J iL (0)) RL J
J
U J ( p ) b a R
R
p
pL R
p
( J iL (0) J ) RLp JR 2
60 p 3200
A( p)
p ( pL R)
p (0.5 p 40) p B1 ( p )
По теореме разложения:
B1 ( p) 0.5 p 40 0, получаем p1 80 1 c
B1' ( p ) (0.5 p 40)' 0.5
A( p1 )
A(0)
3200 60 ( 80) 3200 80t
p1t
u J (t )
e
e
'
B1 (0) p1 B1 ( p1 )
40
( 80) 0.5
80 40 e 80t B