9-10 Уравнения плоскости

1. Плоскость в пространстве

Цель урока:
1) рассмотреть уравнения плоскости в пространстве.
Цель обучения:
11.3.4.3 составлять уравнение плоскости в пространстве;

2. Общее уравнение плоскости

Если в пространстве фиксирована произвольная декартова
система координат Oxyz, то всякое уравнение первой степени с
тремя переменными x y z определяет относительно этой системы
плоскость.
Ax By Cz D 0
(1)
A; B; C; D – некоторые постоянные, причем из чисел A; B; C хотя бы
Общее уравнение плоскости
одно отлично от нуля.
Пусть точка М0(x0; y0; z0) принадлежит плоскости:
Ax 0 By 0 Cz0 D 0 (2)
Вычтем из уравнения (1) тождество (2):
A x x0 B y y 0 C z z0 0
Общее уравнение плоскости
(3)

3. Общее уравнение плоскости

Виды неполных уравнений:
1) D 0;
2) A 0;
Ax By Cz 0 Плоскость проходит через точку О.
By Cz D 0 ll (OX )
z
3) B 0;
Ax Cz D 0
4) C 0;
Ax By D 0 ll (OZ )
ll (OY )
5) A 0; B 0
Cz D 0 ll ( XOY )
6) B 0; C 0 Ax D 0 ll (YOZ )
7) A 0; C 0
0
By D 0 ll ( XOZ ) x
8) B 0; C 0; D 0
Ax 0 x 0
9) A 0; C 0; D 0
By 0 y 0
Cz 0 z 0
10) A 0; B 0; D 0
(YOZ )
( XOZ )
( XOY )
y

4. Уравнение плоскости, проходящей через три точки

Пусть точки М1(х1 ; у1 ; z1 ), М2(х2 ; у2 ; z2 ) и М3(х3 ; у3 ; z3 ) не лежат
на одной прямой.
Тогда векторы: M1M 2 x 2 x1; y 2 y 1; z2 z1
и
M1M 3 x3 x1; y 3 y 1; z3 z1 не коллинеарны.
Точка М(х ; у ; z ) лежит в
одной плоскости с точками
М1 , М2 и М3 только в том
случае, если векторы:
M1M 2 ; M1M 3
и M1M
1
2
1
М
М1
М2
x x ; y y ; z z компланарны.
M M M M M M
1
М3
3
Уравнение плоскости,
проходящей через 3 точки
1
x x1
x 2 x1
x3 x1
1
1
y y1
y 2 y1
y 3 y1
z z1
z2 z1 0
z3 z1

5.

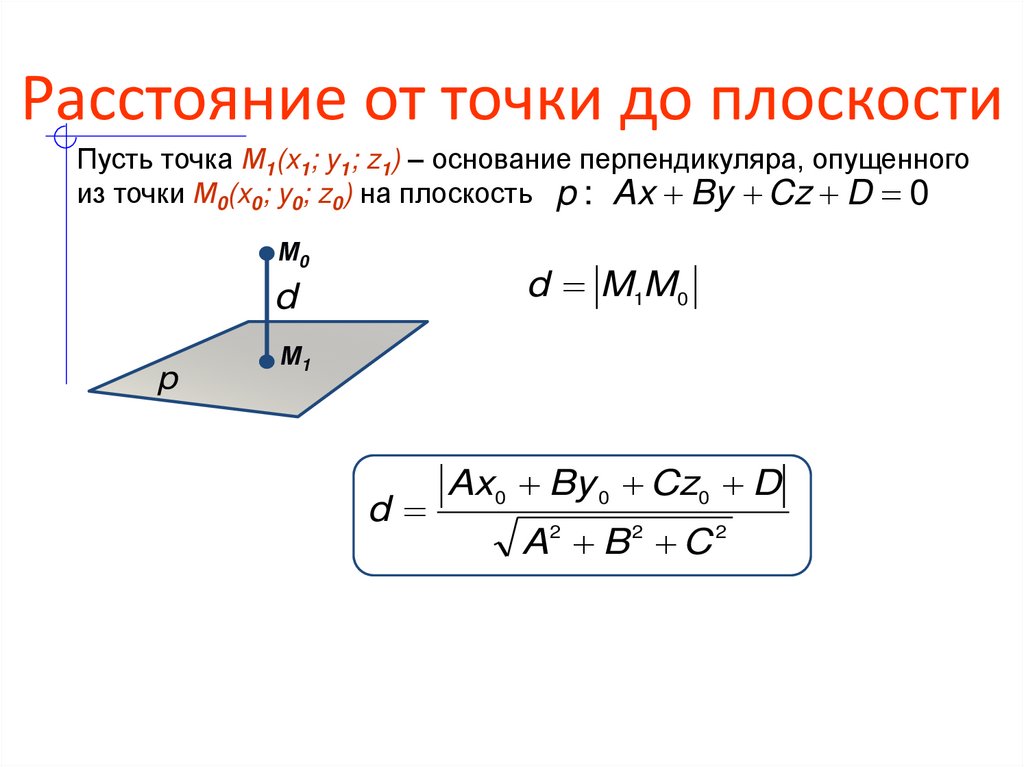
6. Расстояние от точки до плоскости

Пусть точка М1(x1; y1; z1) – основание перпендикуляра, опущенного
из точки М0(x0; y0; z0) на плоскость p : Ax By Cz D 0
М0
d M1M 0
d
p
М1
d
Ax 0 By 0 Cz0 D
A2 B 2 C 2

7.

8.

9.

10.

11.

12.

13.

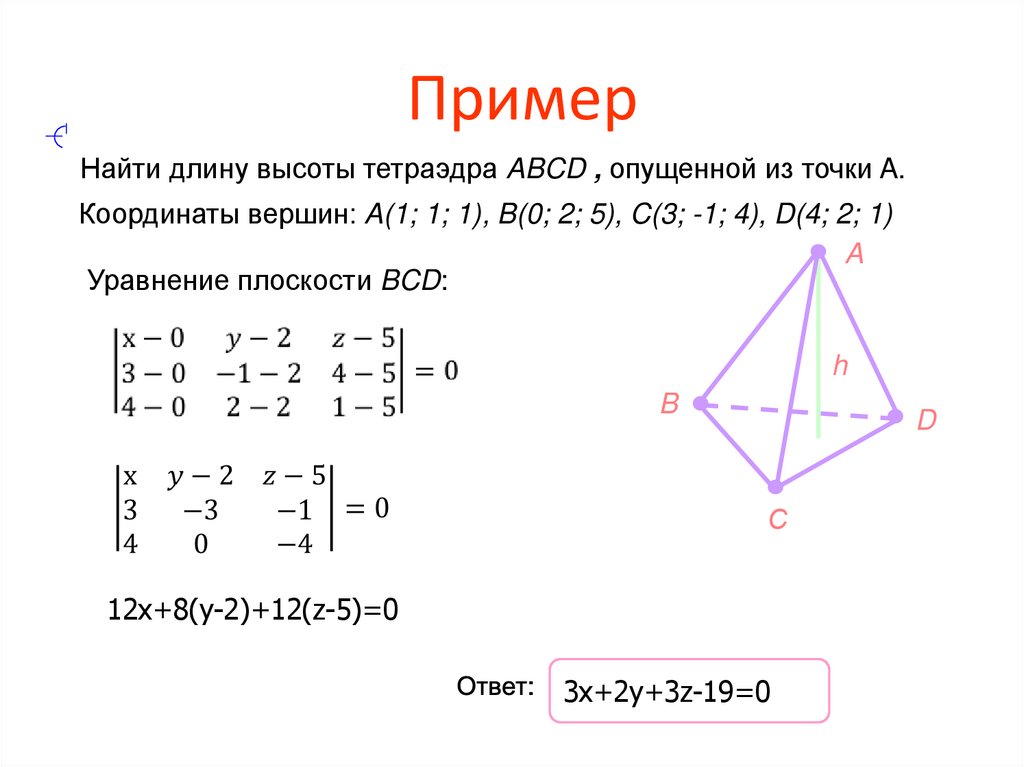
14. Пример

Найти длину высоты тетраэдра ABCD , опущенной из точки A.
Координаты вершин: A(1; 1; 1), B(0; 2; 5), C(3; -1; 4), D(4; 2; 1)
A
Уравнение плоскости BCD:
h
B
D
С
12x+8(y-2)+12(z-5)=0
3x+2y+3z-19=0

15.

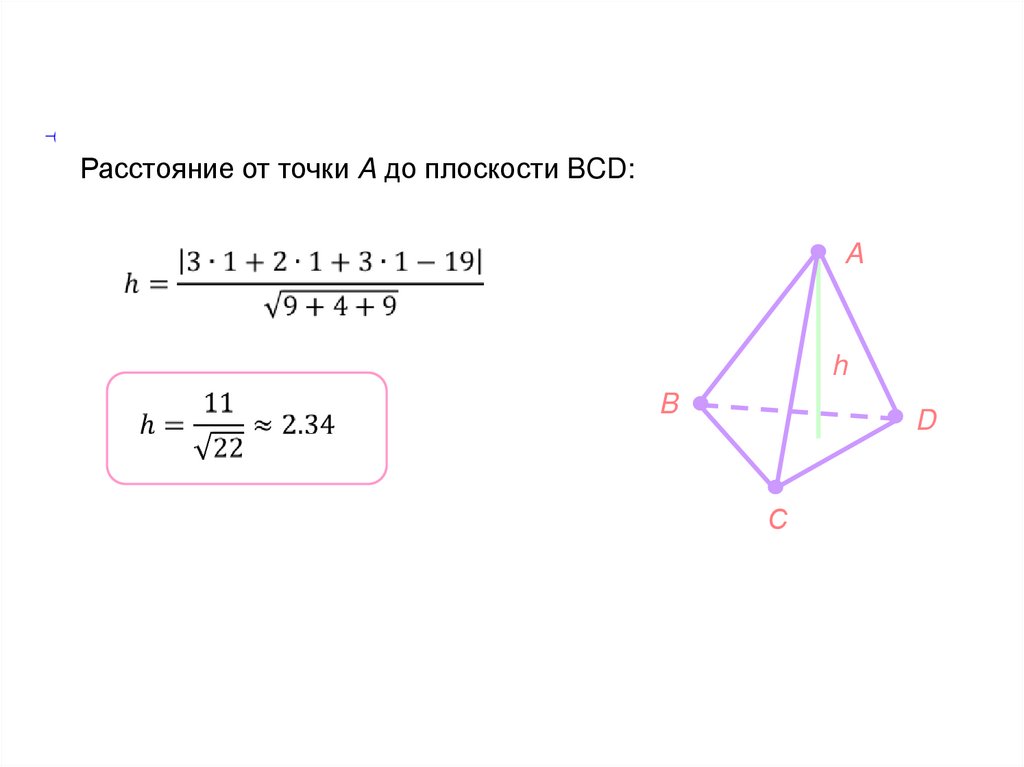
Расстояние от точки A до плоскости BCD:
A
h
B
D
С

16. Упражнение 1

Найдите координаты вектора нормали для
плоскости:
а) 5x-y-1=0;
б) 3x+18z-6=0;
в) 15x+y-8z+14=0;
г) x-3y+15z=0.
Ответ: а) (5, -1, 0);
б) (3, 0, 18);
в) (15, 1, -8);
г) (1, -3, 15).

17. Упражнение 2

Найдите уравнение плоскости, проходящей через точку M(-1, 2, 1), с
вектором нормали, имеющим координаты: а) (0, -5, 2); б) (6, -1, 3); в) (-4,
-2, -1); г) (-3, -8, 0).
Ответ: а) -5y+2z+8=0;
б) 6x-y+3z+5=0;
в) -4x-2y-z+1=0;
г) -3x-8y+13=0.

18. Упражнение 4

В каком случае две плоскости, заданными уравнениями: a1x + b1y +
c1z + d1 = 0, a2x + b2y + c2z + d2 = 0, перпендикулярны?
Ответ: Если выполняется равенство a1a2 + b1b2 + c1c2 =0.

19. Упражнение 5

Перпендикулярны ли плоскости:
а) 2x – 5y + z + 4 = 0 и 3x + 2y + 4z – 1 = 0;
б) 7x – y + 9 =0 и y + 2z – 3 = 0?
Ответ: а) Да;
б) нет.

20. Упражнение 6

Найдите точки пересечения плоскости x + 2y - 3z – 1 = 0 с осями
координат.
Ответ: x = 1, y= 0,5
1
z .
3

21. Упражнение 8

Напишите уравнение плоскости, пересекающей оси координат в
точках:
а) A(1, 0, 0), B(0, 1, 0), C(0, 0, 1);
б) A(1, 0, 0), B(0, 2, 0), C(0, 0, 3);
в) A(1, 0, 0), B(0, -1, 0), C(0, 0, -2).
Ответ: а) x + y + z = 1;
1
1
y z 1;
2
3
1
x y z 1.
2
б) x
в)

22. Упражнение 9

Напишите уравнение плоскости, пересекающей две оси координат в
точках:
а) A(1, 0, 0), B(0, 1, 0);
б) A(1, 0, 0), C(0, 0, 3);
в) B(0, -1, 0), C(0, 0, -2),
и параллельной третьей оси.
Ответ: а) x + y = 1;
1
x z 1;
3
1
в) y z 1.
2
б)

23. Упражнение 10

Напишите уравнение плоскости, пересекающей одну ось координат
в точке:
а) A(1, 0, 0);
б) B(0, 2, 0);
в) C(0, 0, -3),
и параллельной двум другим осям.
Ответ: а) x = 1;
1
y 1;
2
1
в) z 1.
3
б)

24. Упражнение 12

Точка H(-2, 4, -1) является основанием перпендикуляра,
опущенного из начала координат на плоскость. Напишите
уравнение этой плоскости.
Ответ: 2x-4y+z+21=0.

25. Упражнение 13

Составьте уравнение плоскости, проходящей через точку M(1, 3, -1)
и параллельной плоскости:
а) 3x + y – z + 5 = 0;
б) x – y + 5z – 4 = 0.
Ответ: а) 3x +y – z – 7 = 0;
б) x – y + 5z + 7 = 0.

26. Упражнение 14

Напишите уравнение плоскости, проходящей через точки:
а) A (1, 0, 0), B (0, 1, 0), C (0, 0, 1);
б) M(3, -1, 2), N(4, 1, -1), K(2, 0, 1).
Ответ: а) x + y + z – 1 = 0;
б) x + 4y + 3z – 5 = 0.