лекция 8. Геометрия. 2022

1.

Лекция 8
Аналитическая геометрия в пространстве
• Плоскость в пространстве
• Расстояние от точки до плоскости
• Прямая в пространстве
• Взаимное расположение прямой и плоскости

2.

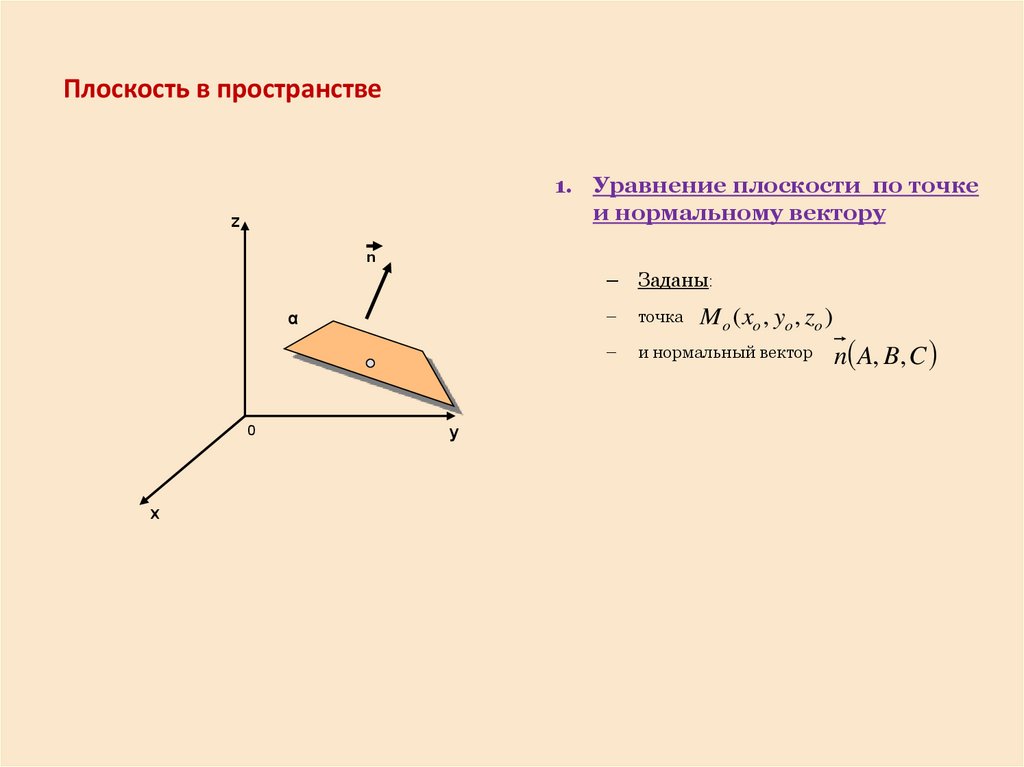
Плоскость в пространстве
1. Уравнение плоскости по точке
и нормальному вектору
z
n
– Заданы:
α
Mo
0
х
y
–
точка
–
и нормальный вектор
M o ( xo , yo , zo )
n A, B, C

3.

Плоскость в пространстве
A( x xo ) B( y yo ) C ( z zo ) 0
Пример.
M o (2, 1,3)
n 1,4,2
1( x 2) 4( y 1) 2( z 3) 0
x 4 y 2z 0

4.

2. Общее уравнение плоскости
Уравнение вида
Ax By Cz D 0
называется общим
уравнением плоскости.
Коэффициенты A,B,C в
уравнении определяют
координаты нормального
вектора: n A, B, C
n A, B, C
α
α

5.

Ax By Cz D 0
Пример:
1( x 2) 4( y 1) 2( z 3) 0
x 4 y 2z 0

6.

3. Уравнение плоскости, проходящей через три заданные
точки
x x1
x2 x1
x3 x1
y y1
y 2 y1
y3 y1
z z1
z 2 z1 0
z 3 z1
M1
M2
M3

7.

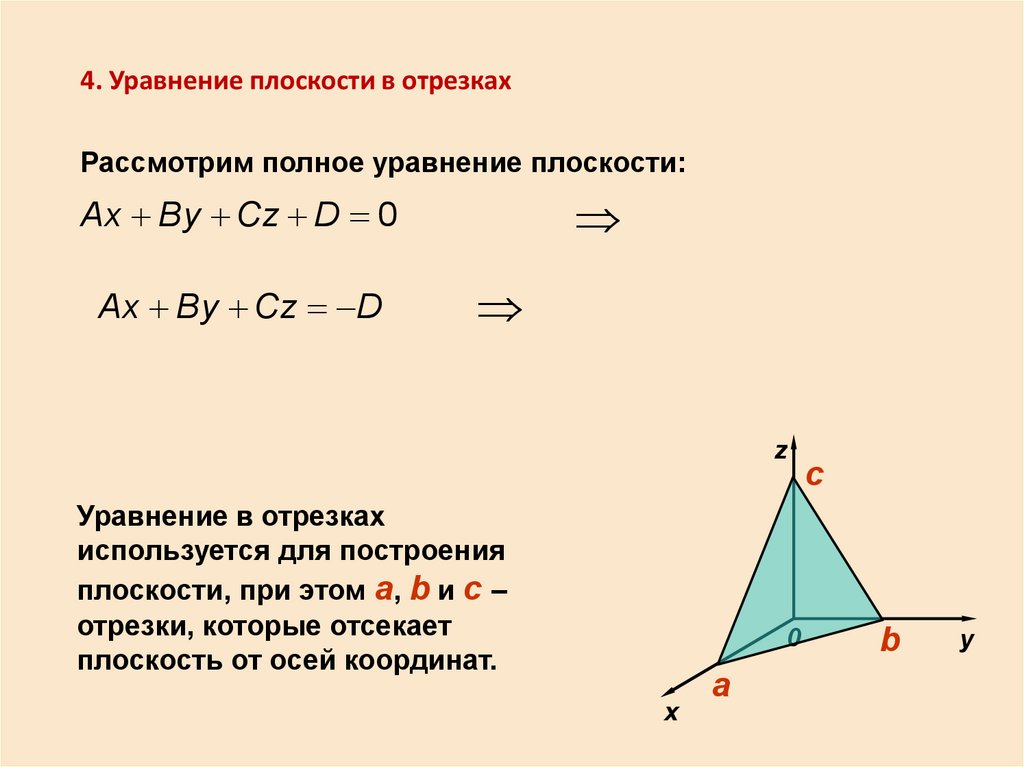
4. Уравнение плоскости в отрезках
Рассмотрим полное уравнение плоскости:
Ax By Cz D 0
Ax By Cz D
z
Уравнение в отрезках
используется для построения
плоскости, при этом a, b и с –
отрезки, которые отсекает
плоскость от осей координат.
с
0
x
a
b
y

8.

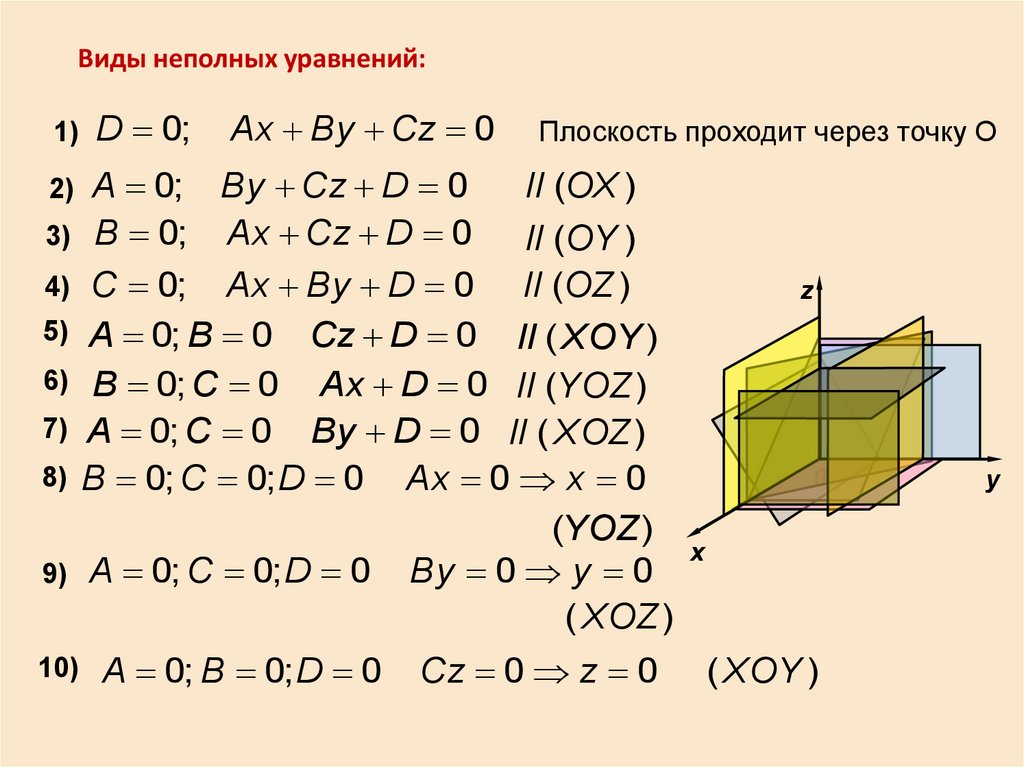
Виды неполных уравнений:
1) D 0;
Ax By Cz 0
2) A 0;
Плоскость проходит через точку O
.
ll (OX )
By Cz D 0
3) B 0; Ax Cz D 0
ll (OY )
4) C 0; Ax By D 0
ll (OZ )
5) A 0; B 0 Cz D 0 ll ( XOY )
6) B 0; C 0 Ax D 0 ll (YOZ )
7) A 0; C 0 By D 0 ll ( XOZ )
8) B 0; C 0; D 0 Ax 0 x 0
(YOZ )
x
9) A 0; C 0; D 0 By 0 y 0
( XOZ )
10)
A 0; B 0; D 0
Cz 0 z 0
z
0
( XOY )
y

9.

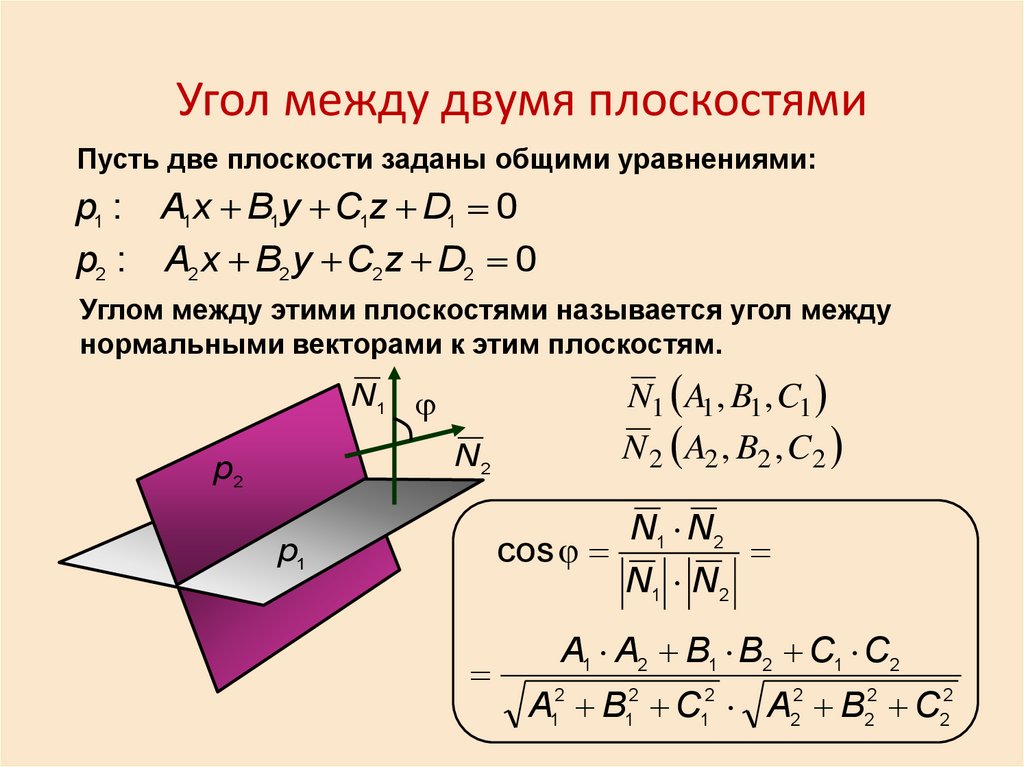
Угол между двумя плоскостями
Пусть две плоскости заданы общими уравнениями:
p1 : A1x B1y C1z D1 0
p2 : A2 x B2 y C2 z D2 0
Углом между этими плоскостями называется угол между
нормальными векторами к этим плоскостям.
N1
N2
p2
N1 A1 , B1 , C1
N 2 A2 , B2 , C2
N1 N2
cos
N1 N2
p1
A1 A2 B1 B2 C1 C2
A12 B12 C12 A22 B22 C22

10.

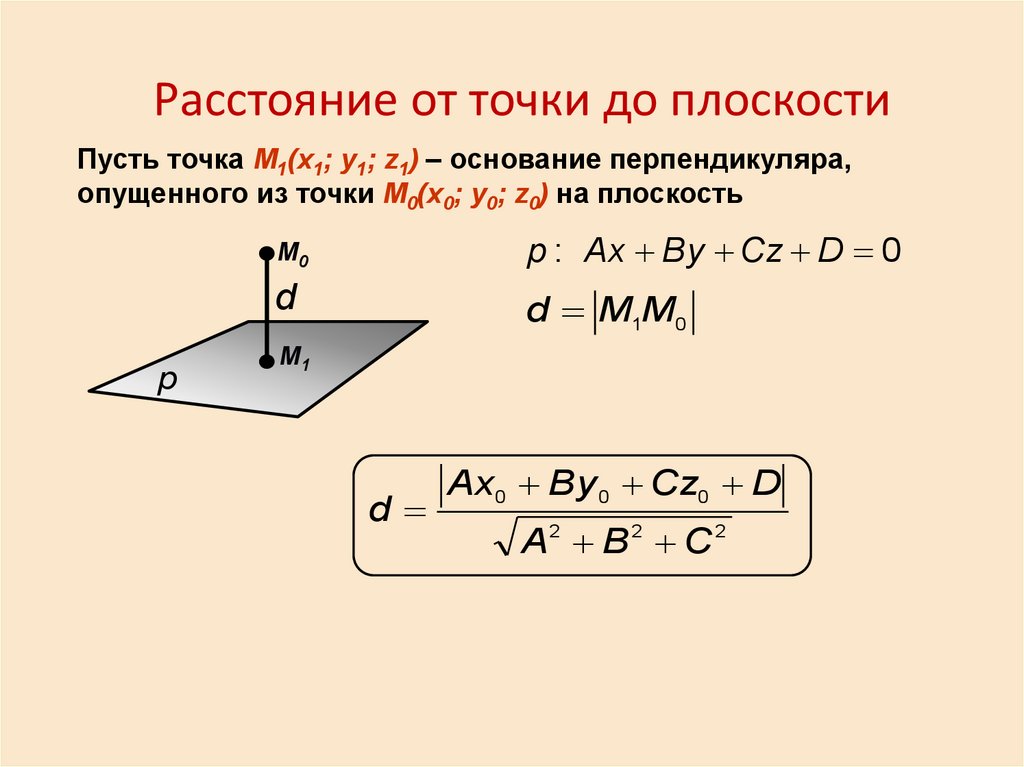
Расстояние от точки до плоскости
Пусть точка М1(x1; y1; z1) – основание перпендикуляра,
опущенного из точки М0(x0; y0; z0) на плоскость
p
М0
p : Ax By Cz D 0
d
d M1M0
М1
d
Ax0 By 0 Cz0 D
A2 B 2 C 2

11.

Прямая в пространстве
1. Общее уравнение прямой
Аксиома: линия пересечения двух
плоскостей – прямая.
A1 x B1 y C1 z D1 0 (Q1 )
l : A x B y C z D 0 (Q )
2
2
2
2
2
Общее уравнение прямой
Q1
Q2
l

12.

2. Канонические уравнения прямой
s m, n, p
l
M o ( xo , yo , zo )
x xo y yo z zo
m
n
p

13.

3. Параметрические уравнения
прямой
x xo
x xo m
m
y yo
y y o n
n
z zo
z z o p
p
x xo m
l : y yo n
z zo p

14.

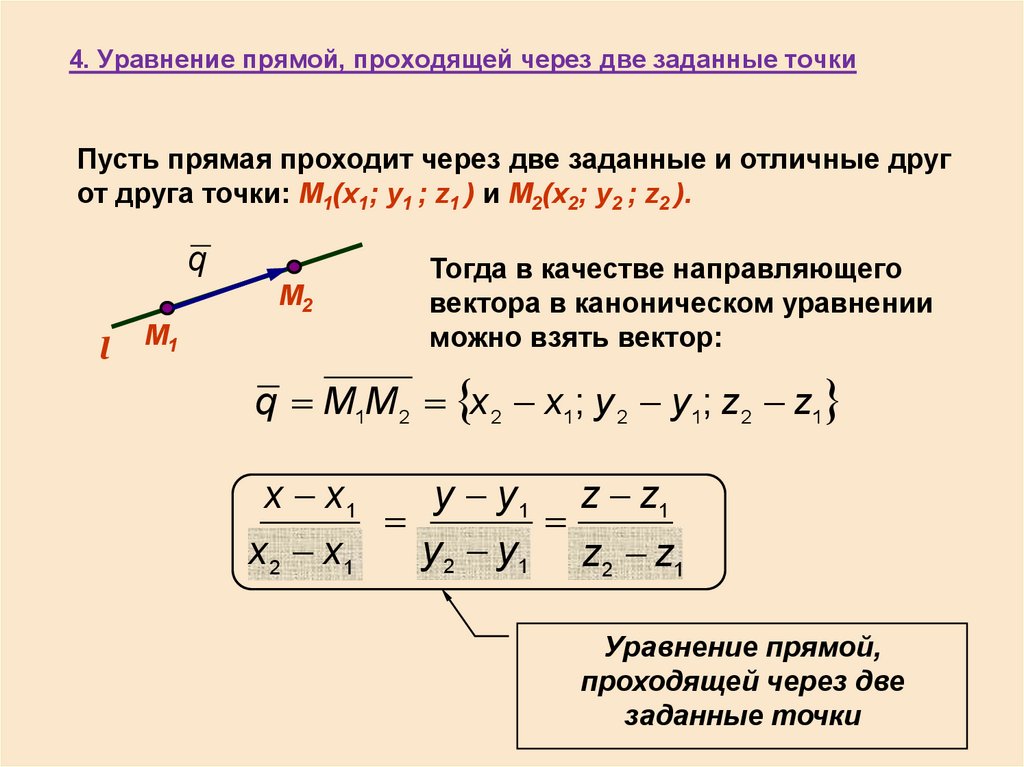
4. Уравнение прямой, проходящей через две заданные точки
Пусть прямая проходит через две заданные и отличные друг
от друга точки: М1(х1; у1 ; z1 ) и М2(х2; у2 ; z2 ).
q
М2
l
М1
Тогда в качестве направляющего
вектора в каноническом уравнении
можно взять вектор:
q M1M 2 x 2 x1; y 2 y 1; z2 z1
x x1
y y 1 z z1
y 2 n y1 z2 p z1
mx1
x2
Уравнение прямой,
проходящей через две
заданные точки

15.

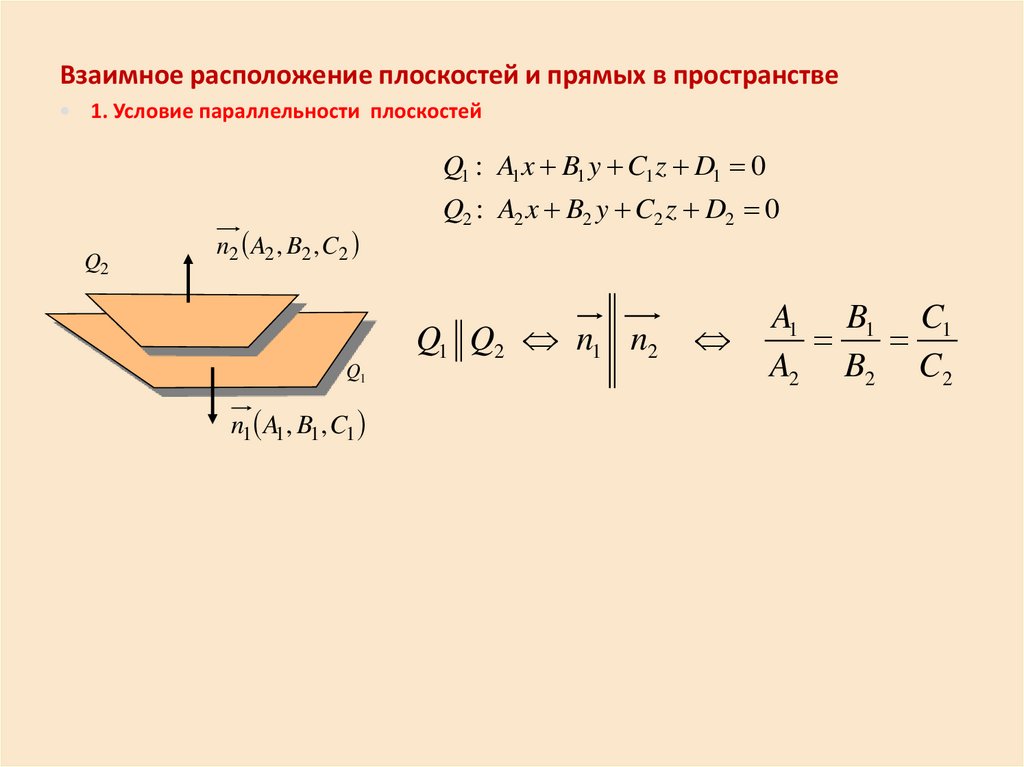
Взаимное расположение плоскостей и прямых в пространстве
1. Условие параллельности плоскостей
Q1 : A1 x B1 y C1 z D1 0
Q2
n2 A2 , B2 , C2
Q2
Q2 : A2 x B2 y C2 z D2 0
Q1 Q2 n1 n2
Q1
n1 A1 , B1 , C1
A1 B1 C1
A2 B2 C2

16.

Взаимное расположение плоскостей и прямых в пространстве
2. Условие перпендикулярности плоскостей
Q1 Q2 n1 n2
A1 A2 B1B2 C1C2 0
Q1
n2
n1
Q2

17.

3. Условие параллельности
прямых
s1 m1 , n1 , p1
l2
l1
s2 m2 , n2 , p2
l1 l2 s1 s2
m1 n1
p1
m2 n2 p2

18.

l1
4. Условие перпендикулярности
прямых
l1 l2 s1 s2
s1 m1 , n1 , p1
m1m2 n1n2 p1 p2 0
l2
s2 m2 , n2 , p2

19.

5. Условие параллельности прямой и
плоскости
s m, n, p
n A, B, C
l
Q
l Q s n s n 0 Am Bn Cp 0

20.

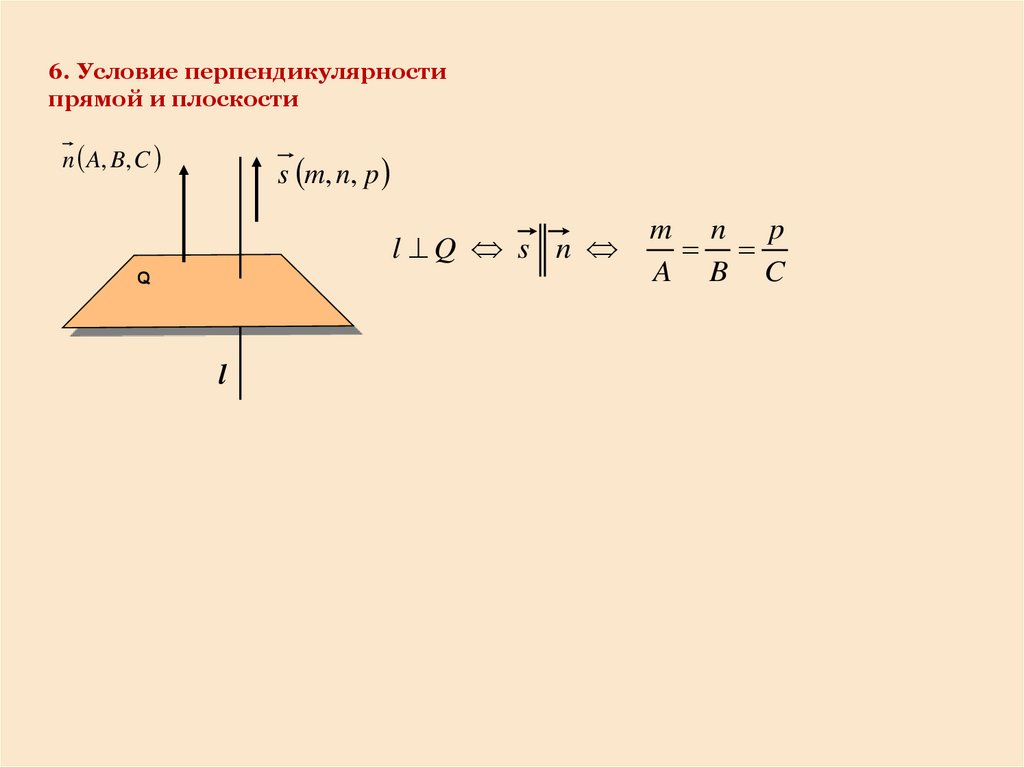
6. Условие перпендикулярности
прямой и плоскости
n A, B, C
s m, n, p
l Q s n
Q
l
m n p
A B C

21.

Угол между прямыми
Пусть две прямые заданы каноническими уравнениями:
x x 2 y y 2 z z2
L2 :
m2
n2
p2
x x1 y y 1 z z1
L1 :
m1
n1
p1
Углом между этими прямыми называется угол между
направляющими векторами к этим прямым.
q1 m1 , n1 , p1
q2 m2 , n2 , p2
cos
q2
q1
L1
L2
m1 n1 p1
L1 ll L2
m2 n2 p2
q1 q2
q1 q2
m1 m2 n1 n2 p1 p2
m12 n12 p12 m22 n22 p22
L1 L2 m1 m2 n1 n2 p1 p2 0

22.

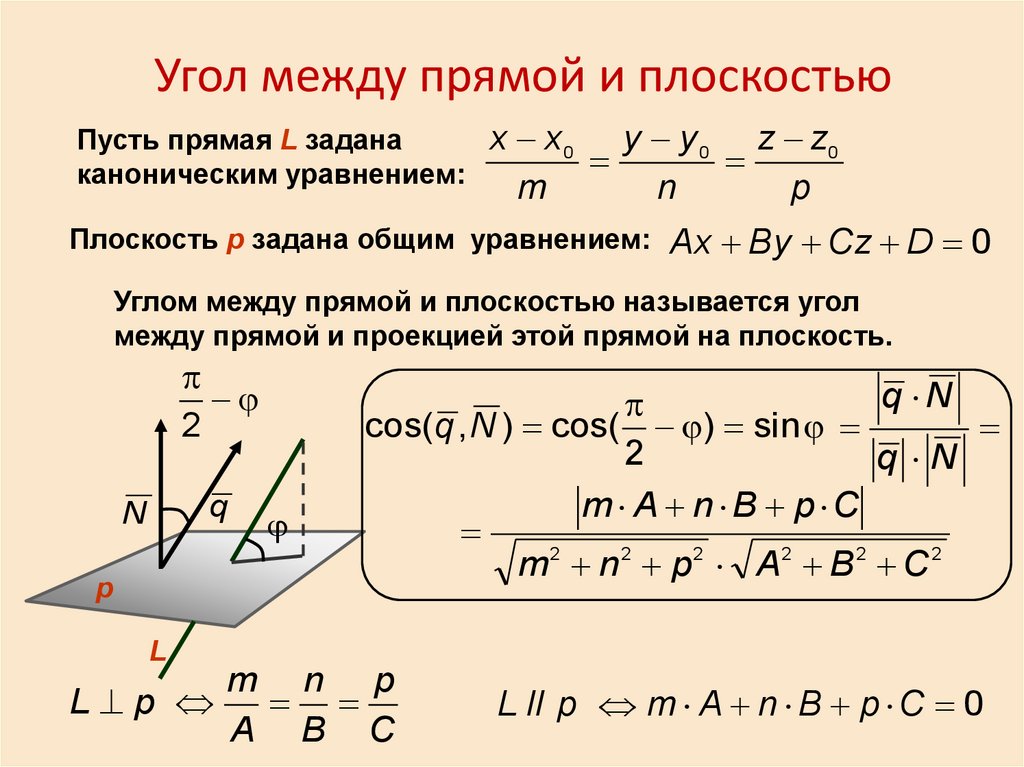
Угол между прямой и плоскостью
Пусть прямая L задана
каноническим уравнением:
x x0 y y 0 z z0
m
n
p
Плоскость p задана общим уравнением: Ax By Cz D 0
Углом между прямой и плоскостью называется угол
между прямой и проекцией этой прямой на плоскость.
2
q
N
р
q N
cos(q , N ) cos( ) sin
2
q N
m A n B p C
m 2 n 2 p 2 A2 B 2 C 2
L
m n p
L p
A B C
L ll p m A n B p C 0

23.

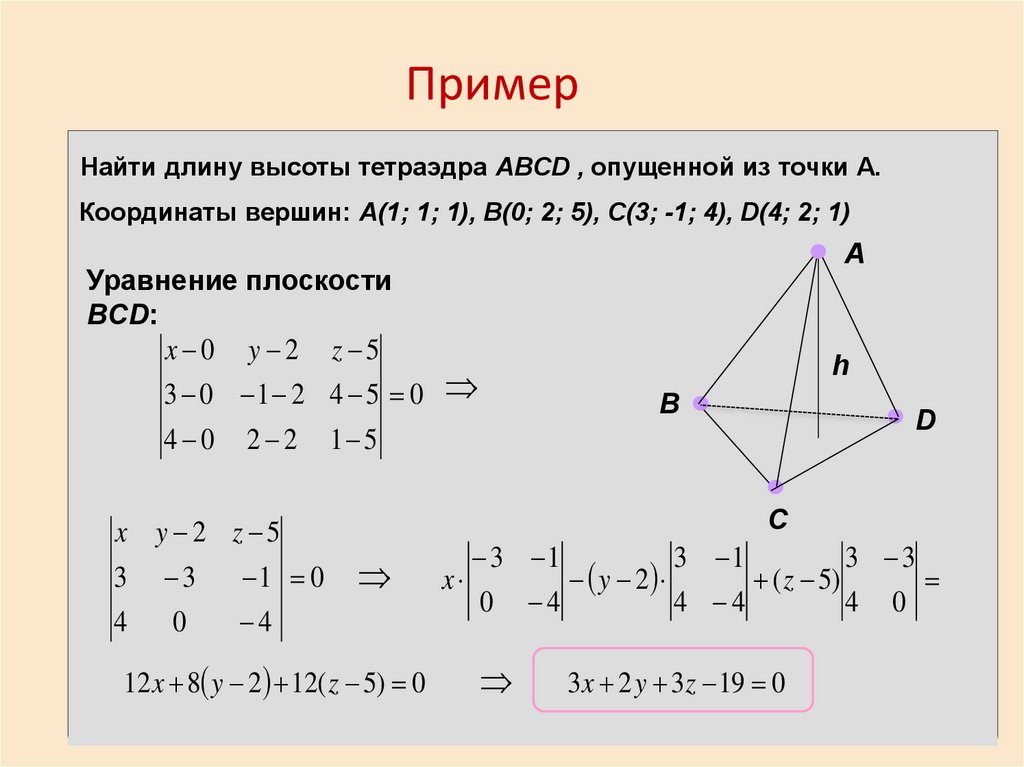
Пример
Найти длину высоты тетраэдра ABCD , опущенной из точки А.
Координаты вершин: A(1; 1; 1), B(0; 2; 5), C(3; -1; 4), D(4; 2; 1)
Уравнение плоскости
BCD:
x 0 y 2 z 5
3 0 1 2 4 5 0
4 0 2 2 1 5
x y 2 z 5
3 3
1 0
4
0
4
A
h
B
D
С
12 x 8 y 2 12( z 5) 0
3 1
3 1
3 3
x
y 2
( z 5)
0 4
4 4
4 0
3x 2 y 3z 19 0

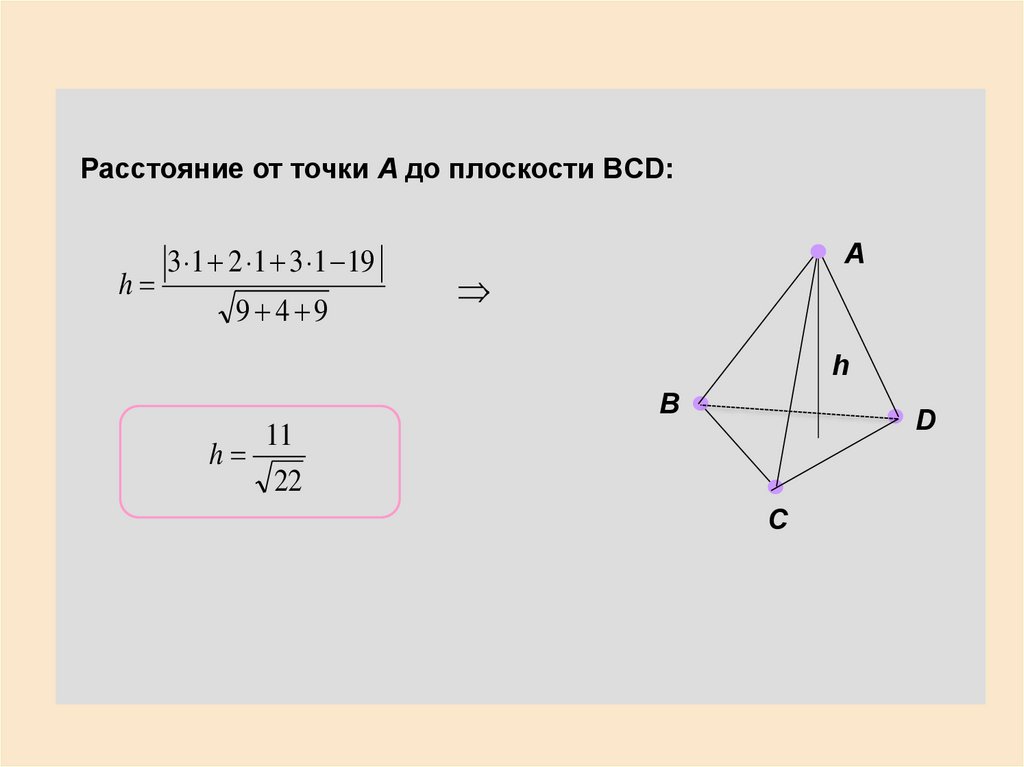
24.

Расстояние от точки A до плоскости BCD:
h
3 1 2 1 3 1 19
9 4 9
A
h
B
D
11
h
22
С

25.

Пример
Найти точку пересечения прямой и плоскости.
x 1 y z 2
3
5
1
y 5z 6 0
Напишем параметрическое уравнение прямой:
Подставим в уравнение плоскости:
5t 5(t 2) 6 0
x 3t 1
y 5t
z t 2
10t 16 0 t 0 1.6
Подставим в уравнение прямой:
x 3 ( 1.6) 1
y 5 ( 1.6)
z 1.6 2
x 3.8
y 8
z 0 .4
K ( 3,8; 8; 0,4)