Плоскость в пространстве

1.

Плоскость в пространстве
Общее уравнение плоскости
Уравнение плоскости в отрезках
Уравнение плоскости, проходящей через три
точки
Угол между двумя плоскостями
Расстояние от точки до плоскости

2.

Уравнение плоскости по точке и
нормальному вектору
М0(x0; y0; z0)
N A; B;C
М(x; y; z) – текущая точка плоскости
N
М0
М
M0M x x0 ; y y 0 ; z z0
M0M N .
Условие перпендикулярности двух
векторов:
A x x0 B y y 0 C z z0 0
Уравнение по точке и нормальному вектору

3.

Общее уравнение плоскости
Если в пространстве фиксирована произвольная декартова
система координат Oxyz, то всякое уравнение первой степени с
тремя переменными x y z определяет относительно этой системы
плоскость.
Ax By Cz D 0
A; B; C; D – некоторые постоянные, причем из чисел A; B; C хотя бы
Общее уравнение плоскости
одно отлично от нуля.
Уравнение по точке и нормальному вектору
A x x0 B y y 0 C z z0 0
N A; B;C
Нормальный вектор
Общее уравнение плоскости называется полным, если все
коэффициенты А; B; C; D отличны от нуля.
В противном случае уравнение называется неполным.

4.

Общее уравнение плоскости
Виды неполных уравнений:
1) D 0;
2) A 0;
Ax By Cz 0 Плоскость проходит через точку О.
By Cz D 0 ll (OX )
z
3) B 0;
Ax Cz D 0
4) C 0;
Ax By D 0 ll (OZ )
ll (OY )
5) A 0; B 0
Cz D 0 ll ( XOY )
6) B 0; C 0 Ax D 0 ll (YOZ )
7) A 0; C 0
0
By D 0 ll ( XOZ ) x
8) B 0; C 0; D 0
Ax 0 x 0
9) A 0; C 0; D 0
By 0 y 0
Cz 0 z 0
10) A 0; B 0; D 0
(YOZ )
( XOZ )
( XOY )
y

5.

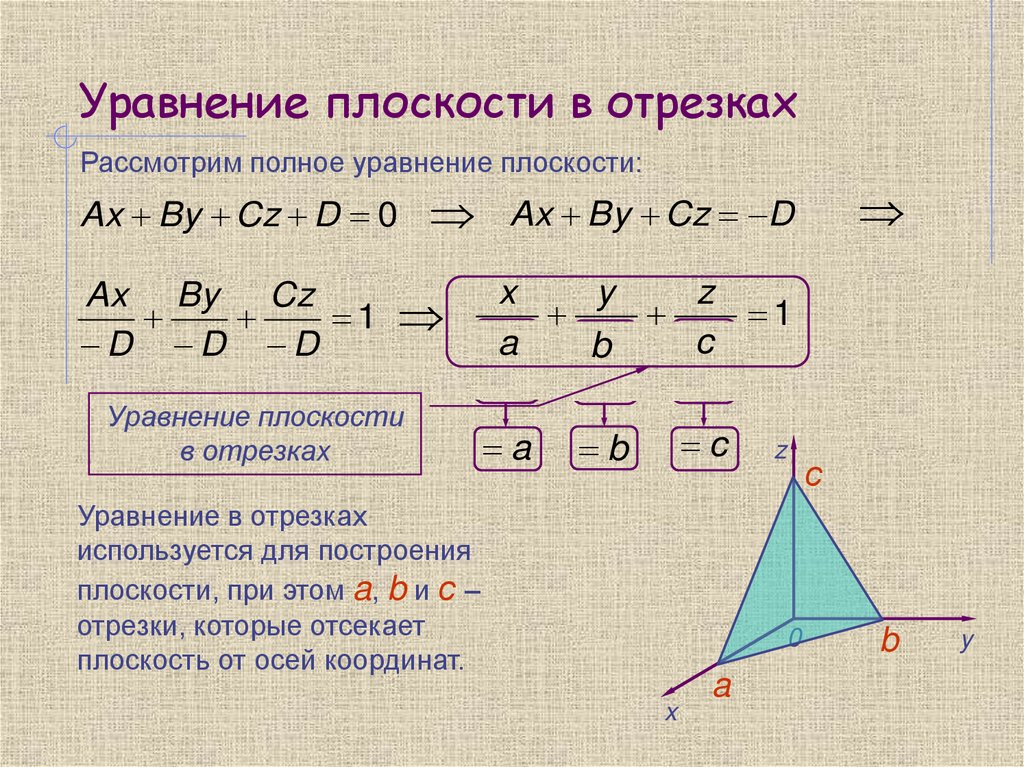
Уравнение плоскости в отрезках
Рассмотрим полное уравнение плоскости:
Ax By Cz D 0
Ax By Cz
1
D D D
Уравнение плоскости
в отрезках
Ax By Cz D
x
y
z
1
aD bD cD
A
B
C
a
c
b
Уравнение в отрезках
используется для построения
плоскости, при этом a, b и с –
отрезки, которые отсекает
плоскость от осей координат.
z
с
0
x
a
b
y

6.

Уравнение плоскости, проходящей
через три точки
Пусть точки М1(х1 ; у1 ; z1 ), М2(х2 ; у2 ; z2 ) и М3(х3 ; у3 ; z3 ) не лежат
на одной прямой.
Тогда векторы: M1M 2 x 2 x1; y 2 y 1; z2 z1
и
M1M3 x3 x1; y 3 y1; z3 z1
Точка М(х ; у ; z ) лежит в
одной плоскости с точками
М1 , М2 и М3 только в том
случае, если векторы:
не коллинеарны.
М3
М1
М
М2
M1M2 ; M1M3 и M1M x x1; y y 1; z z1 компланарны.
M M M M M M
1
1
2
1
3
Уравнение плоскости,
проходящей через 3 точки
x x1
x 2 x1
x3 x1
y y1
y 2 y1
y 3 y1
z z1
z2 z1 0
z3 z1

7.

Угол между двумя плоскостями
Пусть две плоскости заданы общими уравнениями:
p1 : A1x B1y C1z D1 0
p2 : A2 x B2 y C2 z D2 0
Углом между этими плоскостями называется угол между
нормальными векторами к этим плоскостям.
N1
N2
p2
N1 A1; B1; C1
N2 A2 ; B2 ; C2
N1 N2
cos
N1 N2
p1
A1 A2 B1 B2 C1 C2
A12 B12 C12 A22 B22 C22

8.

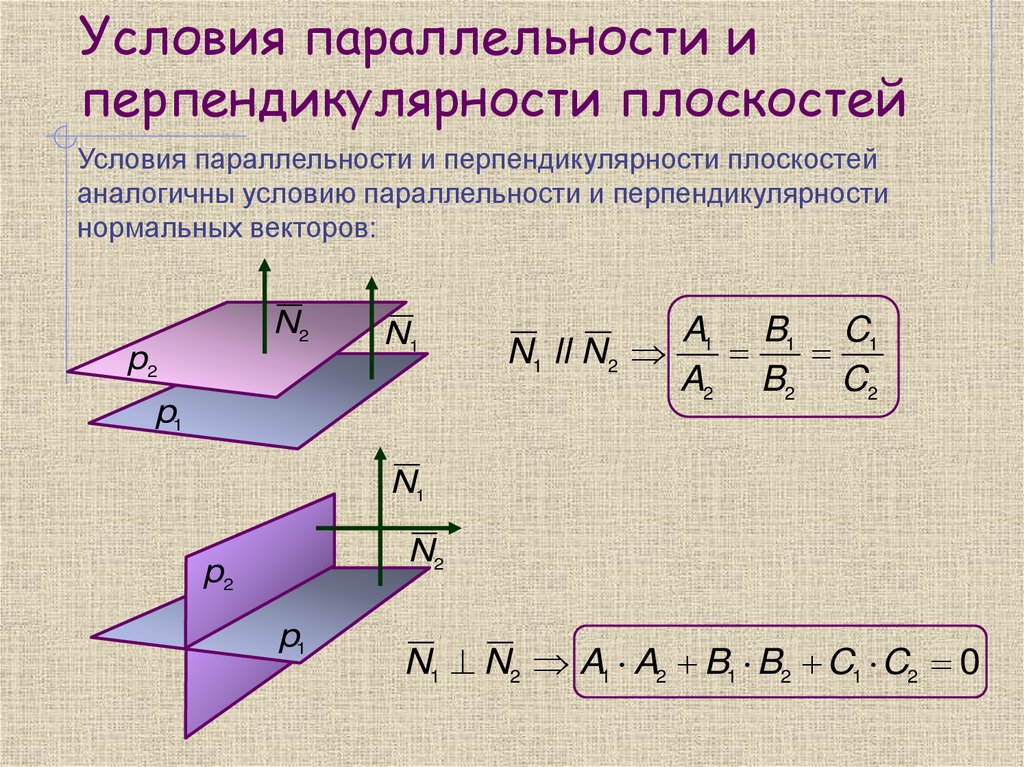
Условия параллельности и
перпендикулярности плоскостей
Условия параллельности и перпендикулярности плоскостей
аналогичны условию параллельности и перпендикулярности
нормальных векторов:
N2
p2
N1
p1
N1 ll N 2
A1 B1 C1
A2 B2 C2
N1
N2
p2
p1
N1 N2 A1 A2 B1 B2 C1 C2 0

9.

Расстояние от точки до плоскости
Пусть точка М1(x1; y1; z1) – основание перпендикуляра, опущенного
из точки М0(x0; y0; z0) на плоскость p : Ax By Cz D 0
М0
d M1M0
d
p
М1
d
Ax0 By 0 Cz0 D
A2 B 2 C 2

10.

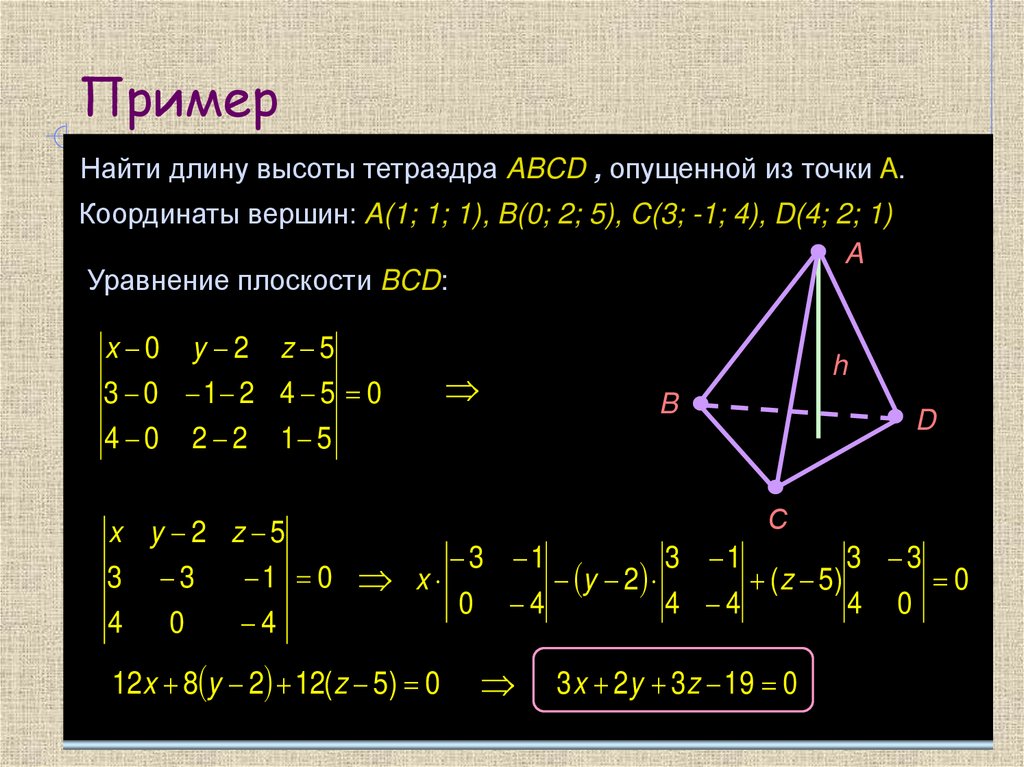
Пример
Найти длину высоты тетраэдра ABCD , опущенной из точки A.
Координаты вершин: A(1; 1; 1), B(0; 2; 5), C(3; -1; 4), D(4; 2; 1)
A
Уравнение плоскости BCD:
x 0
y 2
z 5
3 0 1 2 4 5 0
4 0
2 2
h
B
1 5
С
x y 2 z 5
3
3
1 0
4
0
4
D
x
12x 8 y 2 12( z 5) 0
3 1
0
4
y 2
3 1
4 4
( z 5)
3 x 2y 3z 19 0
3 3
4
0
0

11.

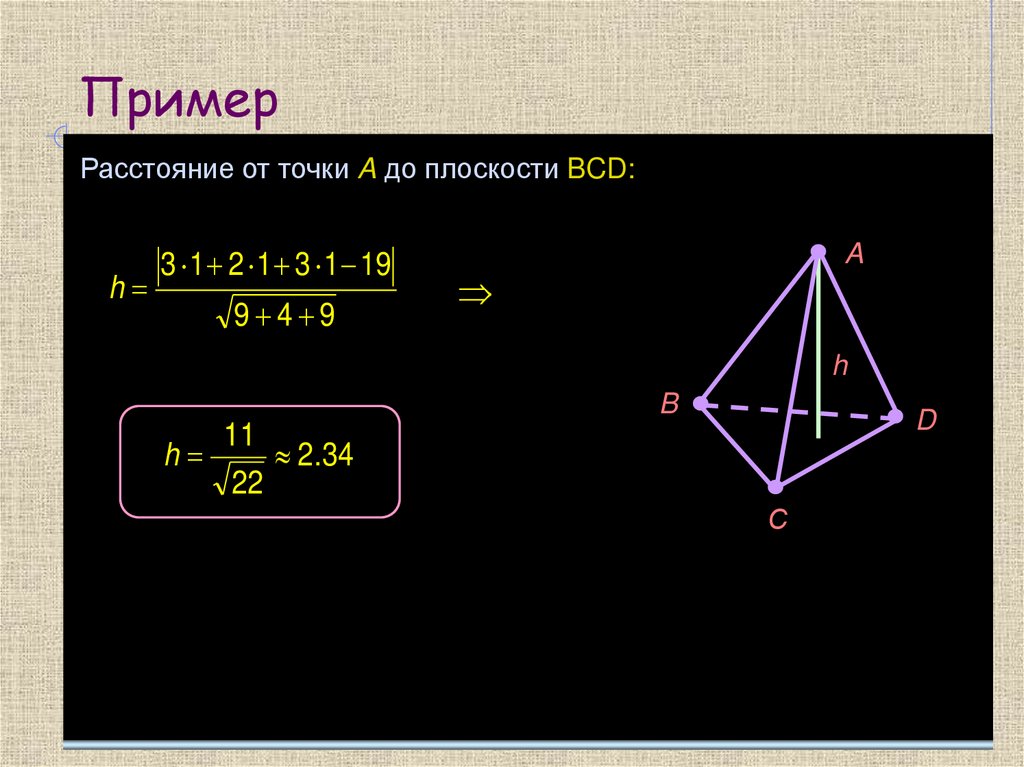
Пример
Расстояние от точки A до плоскости BCD:
h
3 1 2 1 3 1 19
9 4 9
A
h
B
D
11
h
2.34
22
С