Similar presentations:
Плоскость в пространстве
1.
§13. Плоскость впространстве
п.1. Основные формулы.
1) Расстояние между двумя точками в
пространстве.
M 1 ( x1 , y1 , z1 ),
M 1M 2
M 2 ( x2 , y2 , z2 ).
x2 x1 y2 y1 z2 z1 .
2
2
2
2.
2) Деление отрезка в данном отношении.M 1 ( x1 , y1 , z1 ),
M 2 ( x2 , y2 , z2 ).
M 1M
.
MM 2
x1 x2
x
,
1
y1 y2
y
,
1
z1 z2
z
.
1
3.
п.2. Уравнения плоскости.Составим уравнение плоскости, проходящей
через три данные точки
M 1 ( x1 , y1 , z1 ), M 2 ( x2 , y2 , z 2 ), M 3 ( x3 , y3 , z3 ).
M2
M1
M3
M
Точка M(x,y,z) принадлежит плоскости тогда и
только тогда, когда векторы
M 1M , M 1M 2 , M 1M 3
являются компланарными.
4.
По свойству смешенного произведенияM 1M M 1M 2 M 1M 3 0.
Найдем
M 1M ( x x1 , y y1 , z z1 ),
M 1M 2 ( x2 x1 , y2 y1 , z2 z1 ),
M 1M 3 ( x3 x1 , y3 y1 , z3 z1 ).
Тогда
5.
x x1y y1
z z1
x2 x1
y2 y1
z2 z1 0.
x3 x1
y3 y1
z3 z1
Разложим определитель по первой строке
A( x x1 ) B ( y y1 ) C ( z z1 ) 0,
где
A
y2 y1
z2 z1
y3 y1
z3 z1
C
,
B
x2 x1
z2 z1
x3 x1
z3 z1
x2 x1
y2 y1
x3 x1
y3 y1
.
,
6.
Раскроем скобкиAx By Cz Ax1 By1 Cz1 0,
обозначим
D Ax1 By1 Cz1 ,
получим
Ax By Cz D 0
— общее уравнение плоскости.
7.
Вектор, перпендикулярный плоскости,называется нормальным вектором этой
плоскости.
Если плоскость задана уравнением
Ax By Cz D 0,
то вектор
n ( A, B , C )
является нормальным вектором этой
плоскости.
A( x x1 ) B ( y y1 ) C ( z z1 ) 0
— уравнение плоскости, проходящей через
данную точку и перпендикулярную данному
вектору.
8.
Уравнениеx x1
y y1
z z1
x2 x1
y2 y1
z2 z1 0
x3 x1
y3 y1
z3 z1
называется уравнением плоскости,
проходящей через три данные точки.
Уравнение
x y z
1
a b c
называется уравнением плоскости, «в
отрезках» (отсекает от координатных осей
отрезки длиной |a|, |b|, |c|).
9.
п.3. Плоскость. Основные задачи.1) Расстояние от точки до плоскости.
M
M ( x0 , y0 , z0 ),
d
: Ax By Cz D 0,
d
| Ax0 By0 Cz0 D |
A B C
2
2
2
.
10.
2) Угол между плоскостями.n2
n1
: A1 x B1 y C1 z D1 0,
: A2 x B2 y C2 z D2 0.
cos
n1 n2
n1 n2
Угол между
плоскостями равен
углу между
нормальными
векторами этих
плоскостей.
n1 ( A1 , B1 , C1 ),
n2 ( A2 , B2 , C2 ).
A1 A2 B1 B2 C1C2
A12 B12 C12
A22 B22 C22
.
11.
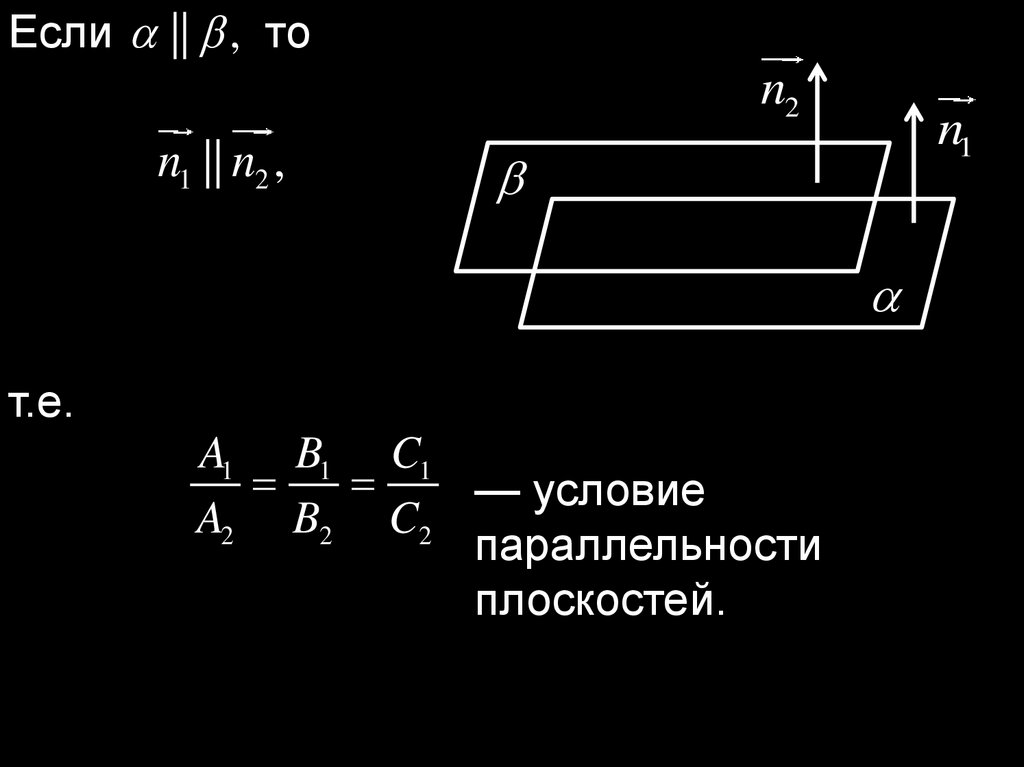
Если || , тоn2
n1 || n2 ,
n1
т.е.
A1 B1 C1
— условие
A2 B2 C2
параллельности
плоскостей.
12.
Если , тоn1 n2 ,
n2
n1
т.е.
A1 A2 B1 B2 C1C 2 0
— условие
перпендикулярности
плоскостей.
13.
Пример. Составить уравнение плоскости,проходящей через точку M(3,2,-1) и
параллельной плоскости
x 2 y 2 z 4 0.
Решение.
Нормальный вектор плоскости x 2 y 2 z 4 0,
n (1, 2, 2),
является нормальным вектором искомой
плоскости.
Тогда требуемое уравнение имеет вид
или
1( x 3) 2( y 2) 2( z 1) 0
x 2 y 2 z 3 0.












 mathematics
mathematics








